在实施双碳目标的背景下，电动汽车（Electric Vehicle，EV）由于其节能环保的优势，将在未来得到大规模普及^[1-2]。2020年11月，国务院办公厅发布了《新能源汽车产业发展规划（2021－2035）》，提出到2025年，我国新能源汽车新车销售量达到汽车新车销售总量的20%左右。根据公安部的统计数据，截至2022年底，全国新能源汽车保有量达1 310万辆，其中纯电动汽车保有量1 045万辆^[3]。中国汽车工业协会发布的数据显示，2022年新能源汽车销量达688.7万辆，市场占有率达25.6%，其中电动汽车销量536.5万辆^[4]，显示出强大的市场活力。

与此同时，电动汽车作为一种新型负荷，其充电负荷的随机性和波动性较强，而电网内整个电动汽车集群可能包括海量的电动汽车，其整体的充电负荷可能与原先的电网基础用电负荷叠加，造成“峰上加峰”的现象，加大电网峰谷差，增大电网安全供电的压力，威胁电网的运行安全^[5-7]。因此，为了有效应对大规模电动汽车充电对电网的冲击，需要较为准确地评估和计算电动汽车集群充电负荷。

关于电动汽车集群充电负荷的计算，一些文献考虑蒙特卡洛模拟法，即通过拟合用户出行和充电习惯相关的概率分布，模拟每个电动汽车的日内充电行为，由此计算大规模电动汽车的整体充电负荷^[8-11]。但已有文献在进行概率拟合时往往较为主观，缺乏较为可靠的统计依据。并且已有文献所考虑的电动汽车类型往往较少，一般只包括私家车、出租车和公交车。随着更多类型汽车的电动化，电动汽车充电负荷的计算也应考虑更多的汽车类型，如网约车和物流车。也有一些文献基于交通运输模型来模拟每个电动汽车的出行和充电行为，并由此计算电动汽车的充电负荷^[12-14]。但该方法需要建立准确的交通运输模型，较为复杂，这限制了该方法的应用。

文章基于蒙特卡洛模拟法，建立了一种适用于大集群电动汽车的充电负荷计算方法，通过概率分布描述电动汽车出行和充电行为的随机性，再利用随机取样模拟各个电动汽车的充电安排，并计算电动汽车集群的总充电负荷，最后将该计算方法应用到2030年南方某省的电动汽车集群。相比已有的计算方法，文章中的方法能够考虑更多的电动汽车类型，包括网约车和物流车，并且可以考虑更多的充电行为细节，包括快慢充和是否白天补电等。

不同类型的电动汽车，其出行和充电规律往往不同^[15-16]。比如，电动私家车往往在上班后工作地点充电或者下班后在家中充电，且大多采用慢充；出租车为了最大化有效运营时间，往往有空就充且采用快充充电。因此，电动汽车集群充电负荷的计算需要对电动汽车进行分类，并考虑各类电动汽车的出行和充电行为特征。

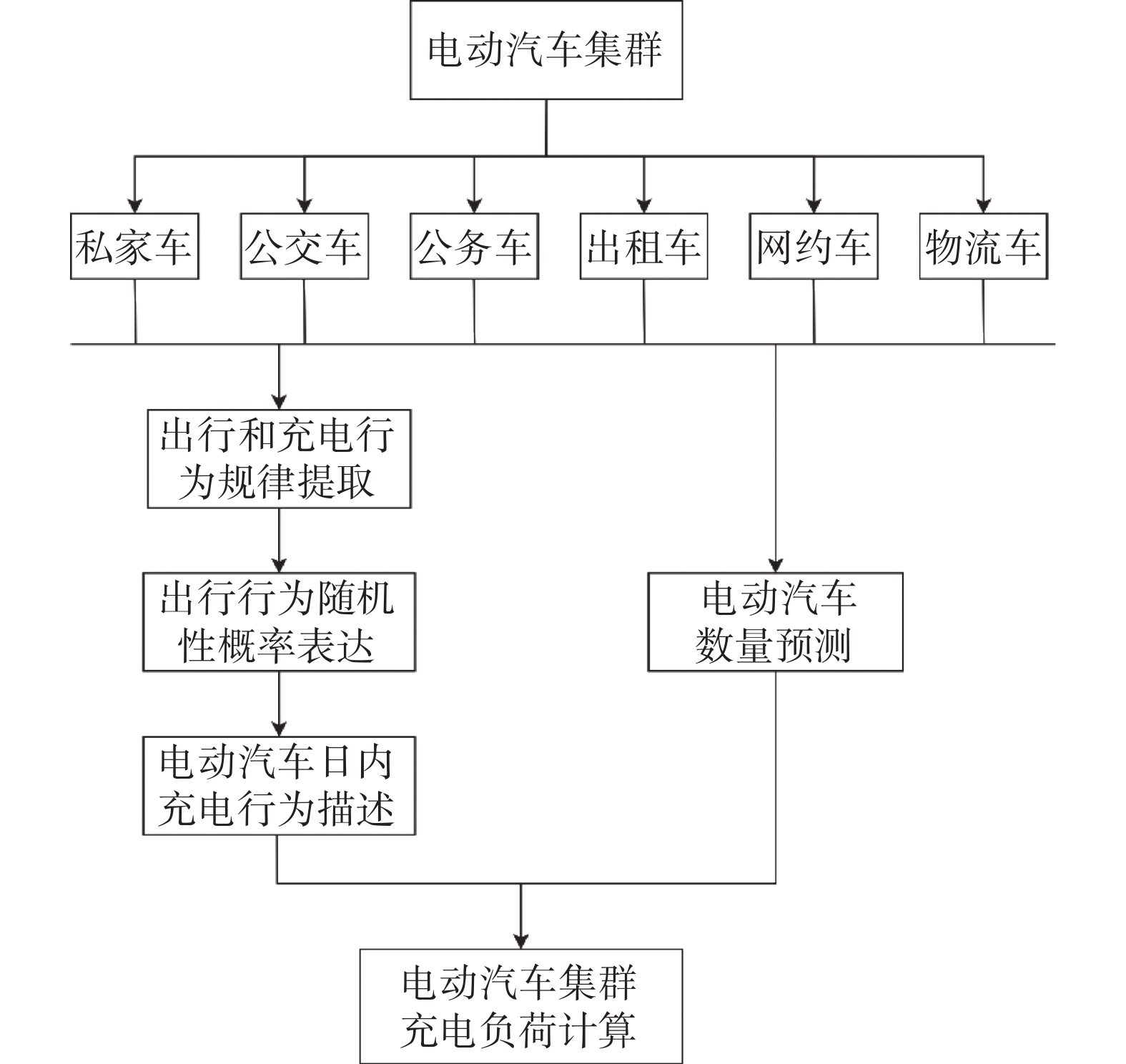
本文中，电动汽车集群充电负荷计算方法的基本结构如图1所示。该方法把电动汽车分为私家车、公交车、公务车、出租车、网约车和物流车共6种。对各类型电动汽车，提取其出行和充电行为规律，再通过概率分布描述其出行和充电行为的随机性，然后，基于电动汽车数量预测，采用蒙特卡洛法计算每一辆电动汽车的日内充电负荷，并将其聚合为整个集群的充电负荷。

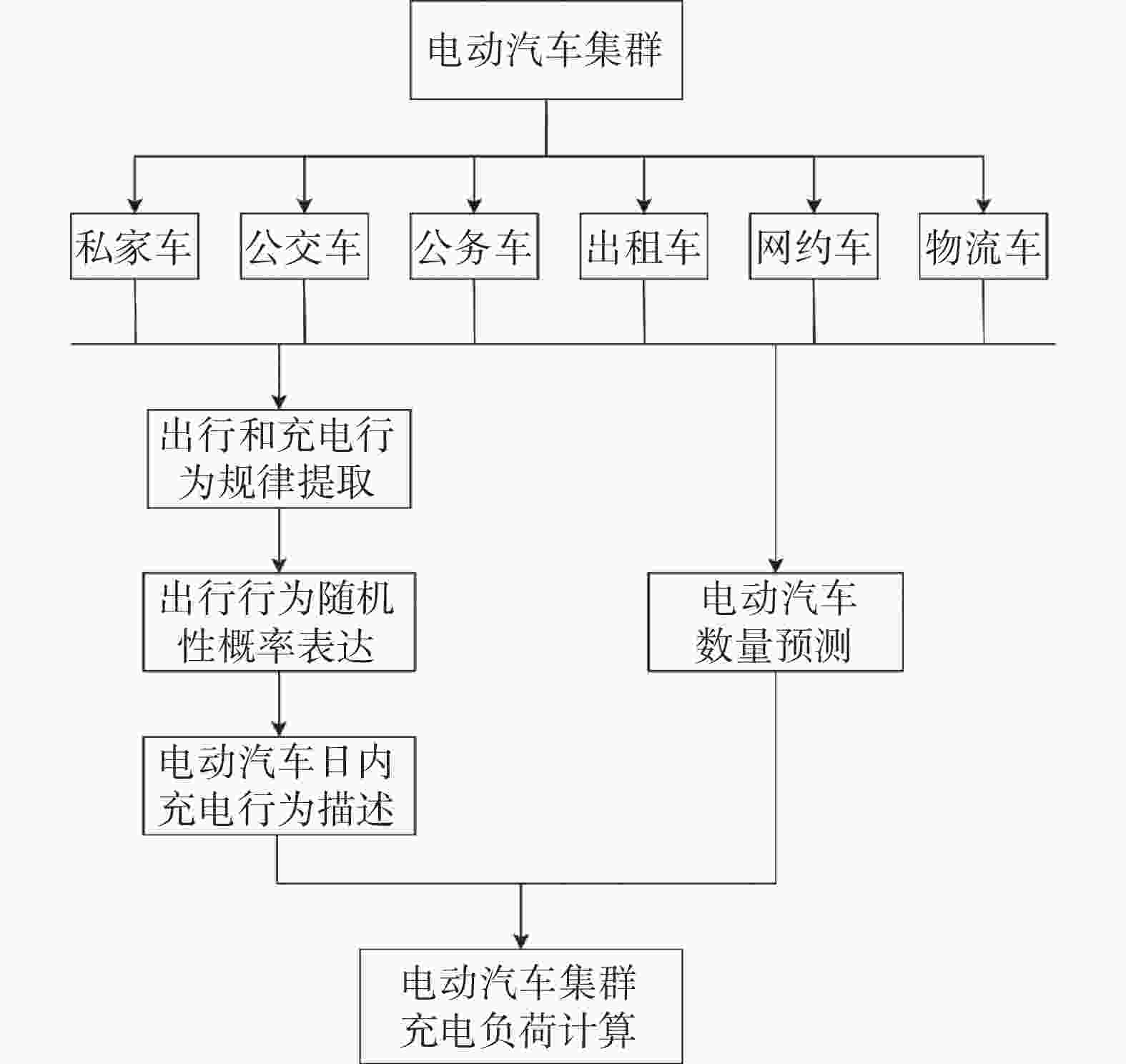
图  1  电动汽车集群充电负荷计算方法的基本结构

Figure 1.  General structure of the charging load calculation method for EV cluster

接下来，本文对各类型电动汽车的出行和充电行为特征进行分析，并由此确定用于描述出行和充电行为随机性的概率分布。

公交车白天按照固定的排班计划运营，一般白天无法长时间充电，因而本文考虑公交车夜晚结束运营后在专门停车场充电。对于行驶里程较长的公交车，可能需要白天短时快速补电以满足全天里程需求。文献[17]的调查发现公交车一般全天充电1~2次，这里假定白天最多补电一次。

公交车的首末班时间分别大体对应着晚上充电的最晚结束时间和最早开始时间。通过查阅南方某市的公交车排班时间表，发现公交车的首末班时间分别集中于5:00－9:00和16:00－24:00之间。通过分布拟合，这里采用正态分布N(7, 0.67)和N(20.5, 1.5)来拟合首末班时间的统计分布。注意这里使用的正态分布表达式为$ N\left(\mu , \, \sigma \right) $，其中$ \mu $为均值，$ \sigma $为标准差。

根据中国新能源汽车大数据研究报告的统计，2021年公交车日均行驶里程位于50~300 km，均值约151 km^[18]，拟合得到统计分布N(151, 55)。本文假定公交车采用快充来充电。

私家车一般选择在家或者工作地点充电。根据文献[17]的统计，私家车在工作地点和家中接入电网的时间分别集中于6:00－11:00和14:00－1:00（次日），这里分别采用N(8.32, 0.85)和N(19.55, 2.06)作为其统计分布。与文献[19]一致，这里假定在家和工作地点充电的私家车占比分别为80%和20%。

报告[18]中的统计结果显示私家车一般日均行驶里程不超过120 km，统计分布符合N(46.3, 15.3)。考虑到私家车全天里程不长，一般单次充满电即可满足全天行驶需求，故这里不考虑私家车在其它时间的补电。根据报告[18]，私家车快充和慢充占比分别为15%和85%。

公务车往往白天用于公务出行，夜晚于工作地点充电，一般没有长途出行的需求。公务车开始充电时间集中于16:00－20:00，统计分布满足N(17.68, 0.76)^[17]。这里假定公务车采用慢充，其它参数的设定与私家车的保持一致。

本文假定出租车运营采用轮班制，即由两位司机每12 h轮流驾驶。文献[17]对电动出租车的开始充电时间进行了统计，其中将一天分成了4块：0:00－8:00、8:00－15:00、15:00－19:00和19:00－24:00，分别对应统计分布N(3.93, 1.86)、N(11.94, 1.36)、N(16.98, 0.9)和N(21.56, 0.98)。

基于报告[18]中的统计数据，出租车单车日均行驶在50~450 km间，统计分布符合N(186, 85)。部分出租车一天行驶里程较长，可能需要一天多充以满足耗电需求。上海市曾对100辆纯电出租车的充电特征进行过统计，结果发现电动出租车日均充电次数2.3次，且约84%的电动出租车每天充2~3次电。因此，本文考虑出租车一天两充。此外，出租车在每次充满电后，一般应等到电池电量降低到一定水平后再考虑充电，因此这里假定出租车有2种充电模式：（1）在0:00－8:00和15:00－19:00充电；（2）在8:00－15:00和19:00－24:00充电。2种模式的占比都设定为50%。

参照文献[17]，这里假定电动出租车采用快充，从而最大化有效营运时间。

报告[18]的统计数据显示，网约车的开始运营时间位于4:00－9:00间，结束运营时间位于18:00－1:00（次日）间，这里分别用N(6.5, 0.83)和N(21.5, 1.17)描述开始和结束运营时间的统计分布。

基于报告[18]的统计数据，网约车单车日均行驶里程在50~400 km间，符合N(184, 62.5)的统计分布。根据报告[18]，网约车快充和慢充占比分别约为75%和25%。

基于报告[18]的统计结果，电动物流车日均行驶里程范围为25~300 km，拟合结果显示其满足N(97, 60)的统计分布。报告[18]还指出电动物流车从上午4:00－10:00出行量不断上升，下午出行高峰发生在15:00－16:00，之后出行量不断下降。本文假定电动物流车于上午4:00－10:00间开始一天的行程（即开始一天运营），统计分布取N(7, 1)；于下午16:00－24:00间结束一天行程（即结束一天运营），统计分布取N(20, 1.33)。

从充电方式看，2021年物流车选择快充的占比由2019年的29.8%提升到了2021年的58.9%^[18]。本文假定未来该占比达到70%。

本文采用蒙特卡洛模拟法来计算整个电动汽车集群的充电负荷。基本思路是基于上一章中对电动汽车出行时间和里程及充电习惯相关的统计分布进行随机取数，提取各个电动汽车的出行和充电行为，由此模拟其一天内的充电安排并计算日内充电负荷，进而计算整个集群的总充电负荷。

该方法还需要以下假设：

1）公交车、网约车和物流车结束一天营运的时间就是开始充电的时间。

2）对于一天内行驶里程较长的公交车、网约车和物流车，其会于白天额外快速补电。这里假设快速补电发生在开始和结束运营时间的中间时刻，且补电功率取各类电动汽车的快充功率。对其它类型电动汽车，考虑其一天里程较短或一天多次快充，这里假定除了上一章描述的充电之外，其不需要额外补电。

3）对各类型电动汽车，不管慢充或快充，充电效率始终设定为95%。

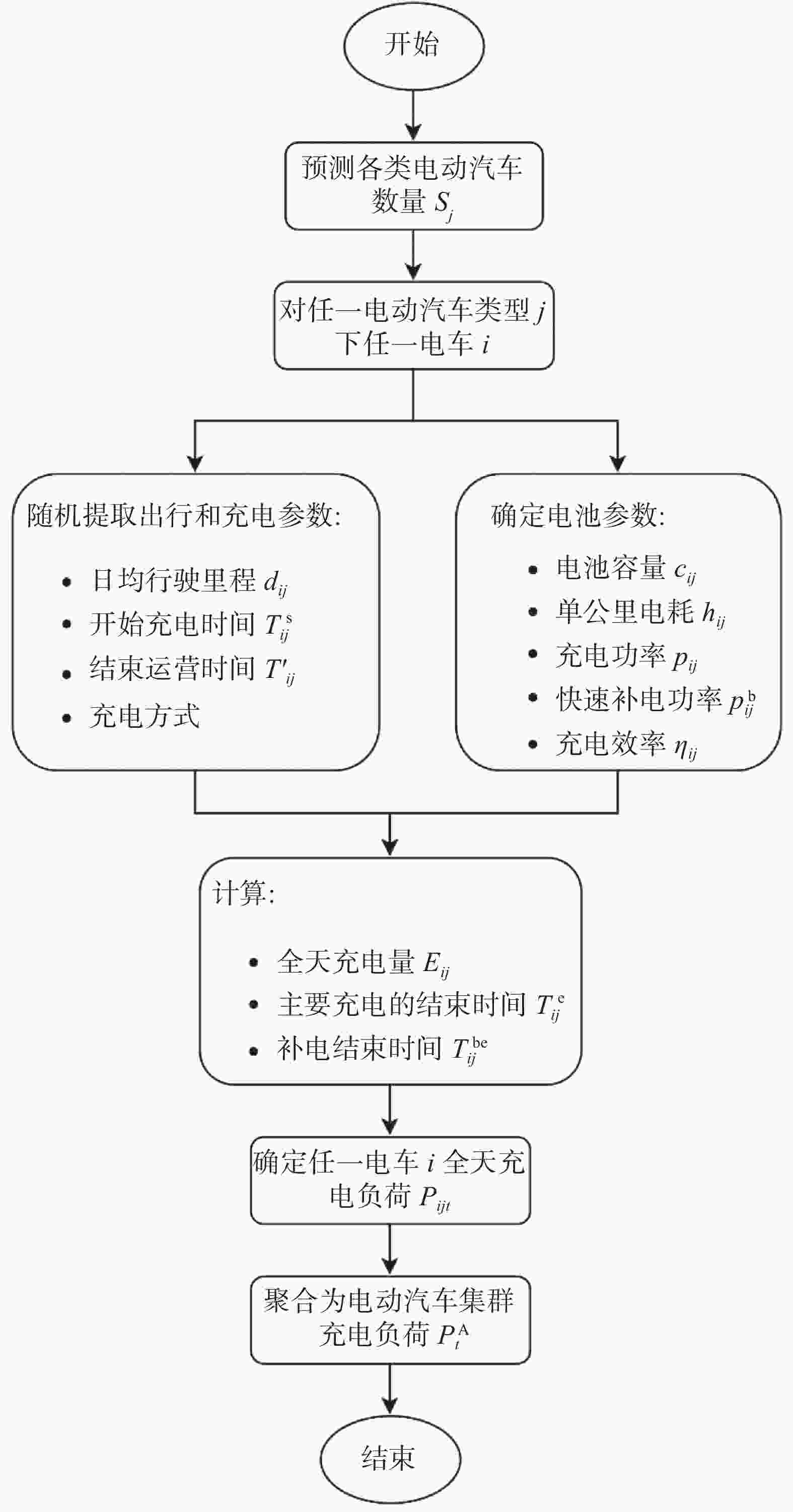
电动汽车集群充电负荷的计算步骤如图2所示。

图  2  电动汽车集群充电负荷计算步骤

Figure 2.  Calculation steps of the charging load for EV cluster

图2中的各步骤将在以下各节中详细解释。

关于电动汽车数量的预测，当前已有较多方法，包括弹性系数法、千人保有量法和基于Bass模型的预测法等^[20-21]，这里不再赘述，具体可参考有关文献。此外，对于公交车、出租车和公务车，其数量在短期内可能不会发生太大变化，可结合其规模发展趋势和政府政策进行预测^[17]。

本文考虑表1中的电动汽车电池参数设定。电动公交车电池参数参考比亚迪B10。其它类型电动车电池参数根据近三年畅销车型而定。需要特别指出的是：

1）电动物流车车型众多，本文根据电池参数将电动物流车分为4类（见表1）。根据有关统计，各大类物流车近三年的年均销量占比分别约为73%、10%、4%和13%^[22]，这里假定未来各类物流车保有量也保持着相同的占比分布。

2）根据《新能源汽车产业发展规划（2021－2035年）》，2025年纯电动乘用车新车平均电耗需降至0.12 kWh/km。参考文献[9]，这里假定电动车额外需要20%的电力用于空调制冷，则乘用车（包括私家车、公务车、出租车和网约车）电耗为0.144 kWh/km。

假定各类型电动汽车数量的预测结果为$ {S}_{j} $，$ j $=1, 2, $ \cdots $, 6。对于每一类电动汽车$ i $，考虑属于该类的所有电动汽车$ i $=1, 2, $ \cdots $, $ {S}_{j} $，基于第一章中关于各类电动车出行和充电行为的概率分布，随机提取每个电动车的日均行驶里程、充电开始和最晚结束时间以及充电方式（快或慢充），然后结合表1中的代表性电池参数设定确定每个电动车的电池参数。表2归纳了用于充电负荷计算的电动汽车参数。

对电动汽车$ i $=1, 2, $ \cdots $, $ {S}_{j} $，一天内所需充电量$ {E}_{ij} $可通过式（1）计算：

不同类型电动车充电负荷的计算公式也有区别。

1）私家车和公务车

对于这2类电动车，充电结束时间$ {T}_{ij}^{{\mathrm{e}}} $计算式为式（2）：

一天内电网侧的充电负荷可用式（3）计算：

式中：

$ t $——时间。

2）公交车、网约车和物流车

对于这些电动车，首先通过式（4）判断是否需要在白天快速补电：

式中：

$ {\delta }_{ij} $−车主能接受的最低电池电量百分比，本文取25%；

$ {p}_{ij}{\eta }_{ij}\left({T'}_{ij}-{T}_{ij}^{{\mathrm{s}}}\right) $和$ {c}_{ij}\left(1-{\delta }_{ij}\right) $为考虑充电时长限制和电池容量限制的最大可充电量，两者中的最小值代表了实际最大可充电量，而如果其小于当天耗电量，则需要白天快速补电。

相对应的，快速补电的补电量$ {E}_{ij}^{{\mathrm{b}}} $为式（5）：

补电开始时间$ {T}_{ij}^{{\mathrm{bs}}} $和补电结束时间$ {T}_{ij}^{{\mathrm{be}}} $分别为式（6）～式（7）：

快速补电对应的充电负荷如式（8）所示：

考虑白天补电之后，夜间正式充电所对应的负荷的计算式也可参照式（2）~式（3），其中需要将$ {E}_{ij} $替换为$ {E}_{ij}-{E}_{ij}^{{\mathrm{b}}} $。

最后，将白天补电和夜间正式充电的负荷加合在一起，就是完整的日内充电负荷，即式（9）：

3）出租车

出租车一天内有2次充电，假定2次充电之间的行驶距离为一天行驶距离$ {d}_{ij} $的一半，则第一次充电所对应负荷的计算如式（10）~式（11）所示：

式中：

$ {T}_{ij}^{{\mathrm{st}}1} $——第一次充电开始时间；

$ {T}_{ij}^{{\mathrm{et}}1} $——第一次充电结束时间。

第二次充电负荷$ {P}_{ijt}^{T2} $的计算可参照式（10）~式（11），只需要将$ {T}_{ij}^{{\mathrm{st}}1} $更换为第二次充电的开始时间$ {T}_{ij}^{{\mathrm{st}}2} $。

最后将2次充电的负荷$ {P}_{ijt}^{T1} $和$ {P}_{ijt}^{T2} $在时间上加和在一起，就得到了一天内完整的充电负荷。

在得到各个电车的全天充电负荷之后，将某个时间点上某类电动汽车下各个电车的充电负荷进行加和，就得到了该时间点上该类电动汽车的总充电负荷$ {P}_{jt}^{{\mathrm{A}}} $，由此可以确定该类电动汽车全天充电负荷曲线如式（12）所示：

将某个时间点上各类电动汽车的总充电负荷$ {P}_{jt}^{{\mathrm{A}}} $进行加和，就得到了该时间点上整个电动汽车集群的充电负荷$ {P}_{t}^{{\mathrm{A}}} $，由此就可以得到全天充电负荷曲线如式（13）所示：

本文将南方某省电动汽车集群作为仿真案例。结合有关政府文件，该省2030年的各类电动汽车数量的预测结果见表3。其中，电动私家车考虑低、高2种场景，对应着不同的私家车电动化程度，而对其它类型电动汽车的数量，结合2020年实际数量和有关机构对2025年的数量预估进行线性回归预测。

基于表3，对2030年各类型电动汽车和整个电动汽车集群的充电负荷进行计算，结果如图3~图5所示，相对应的峰值负荷和其发生时间也被提取出来，结果见表4。

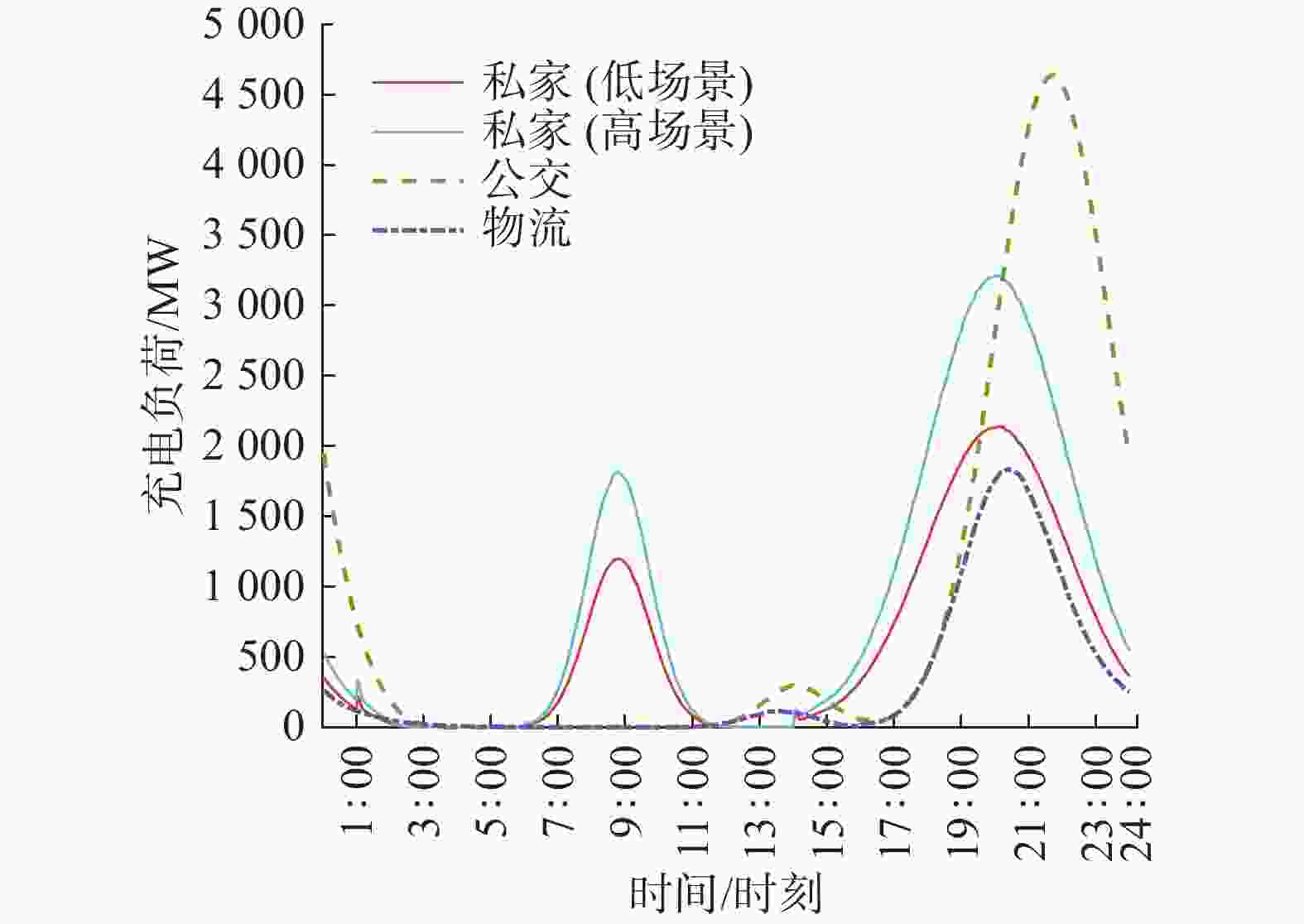
图  3  电动私家车、公交车和物流车的充电负荷曲线

Figure 3.  Charging load curves of private EVs, electric buses and logistics EVs

图  4  电动公务车、出租车和网约车的充电负荷曲线

Figure 4.  Charging load curves of official EVs, electric taxis and online ride-hailing EVs

图  5  不同场景下电动汽车集群的充电负荷曲线

Figure 5.  Charging load curves of EV cluster under different scenarios

由图3可见，公交车充电负荷高峰在20:00－23:00之间，充电负荷在18:00－21:00间快速上升，而在过了21:00后迅速下降。私家车总充电负荷曲线有2个高峰，一个位于18:00－22:00，另一个位于8:00－10:00，分别对应夜间在家中和白天在工作地点充电。但白天的峰值比夜晚的要低很多，低约44%，这是因为相对更少的私家车选择在工作地点充电。

根据图4，电动物流车、公务车和网约车的充电高峰分别位于19:00－22:00、17:00－19:00和21:00－23:00间，即在其结束白天服务或运营之后。电动出租车有4个较为接近的充电负荷峰值，分别位于约4:30、12:00、17:00和21:30。

图3还反映公交车和物流车在白天11:00－16:00间也有一定的充电负荷，这说明有一部分公交车和物流车由于夜晚充电时长或者电池容量的限制，所充电量无法满足全天耗电需求，需要在白天快速补电。

表4显示在所有电动汽车类型中，公交车有着最高的充电负荷峰值，达到4 639.5 MW，虽然数量上私家车是公交车的20~30倍，但其充电负荷峰值最高只有3 210.4 MW，不到公交车的70%。这主要是因为公交车日均行驶里程较高且每公里耗电量较大，导致每天充电量较大，即使采用快充，其充电时间也不会很短，这样就会出现大量公交车在某个时刻同时充电，再考虑其较高的充电功率，充电负荷峰值自然较高。相比之下，虽然电动私家车数量高很多，但其日均行驶里程和耗电水平都要低很多，每天所需充电量较低，再考虑其大部分采用慢充，充电负荷峰值也就不会特别高。

表4中的结果同样反映，电动私家车普及程度对其总充电负荷峰值影响较大。比如2030年，高场景下的私家车充电负荷峰值比低场景下的高约50%。可以预计的是，随着未来电动私家车数量的继续增长，其充电负荷峰值也将增大，甚至可能超过电动公交车的充电负荷峰值。此外，表4还显示，相比其它车型，电动出租车的负荷水平要低很多，这主要有2方面原因：（1）电动出租车相比其它类型电动车数量较低；（2）出租车的开始充电时间在一天内分布比较分散，并且因为采用快充而充电时间较短，较难出现大量出租车在某个时刻同时充电。

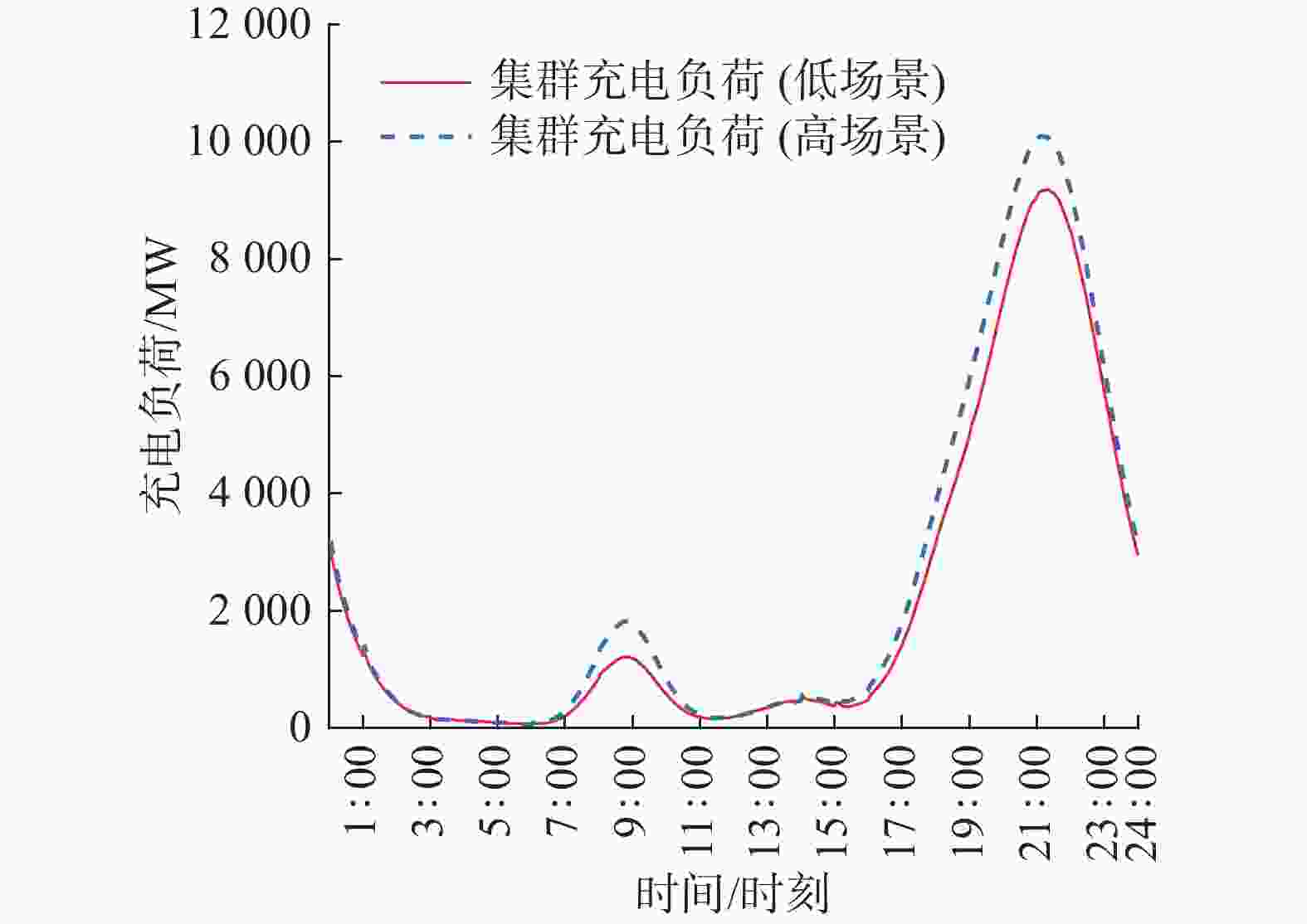
根据表4和图5，整个电动汽车集群的充电高峰在19:00－23:00间，峰值时间在21:10－21:20之间，峰值最高可达10.092 7 GW。电动汽车集群在白天8:00－10:00间也有一个充电高峰，但其只有夜间峰值的18%~20%。应该指出的是，表4中集群的充电负荷峰值不是各类型电动汽车充电负荷峰值的简单累加，这是因为不同类型电动汽车充电负荷峰值往往发生在不同时间，比如公务车的峰值时间比较早，而公交车的最晚。此外，低场景和高场景下集群充电负荷曲线间的区别反映了不同场景下电动私家车充电负荷间的差别。

本文提出了一种电动汽车集群充电负荷的计算方法，可以考虑从私家车、公交车、出租车、公务车、网约车到物流车共6种电动车型，能够利用概率模型描述各类车型出行和充电行为的随机性，并考虑快慢充和白天快速补电等充电细节。

本文以南方某省作为仿真案例，结果显示所提出的方法能够提供各类型电动汽车和整个集群的日内充电负荷曲线，并可以给出相对应的负荷峰值大小和峰值发生时间。案例分析也发现在所有电动汽车类型中，公交车的充电负荷峰值最高，达到4 639.5 MW，其次是私家车，不到公交车的70%，而出租车的最低，只有198.9 MW。虽然数量上电动私家车是电动公交车的数十倍，但公交车充电量更大且充电功率更高，公交车充电负荷峰值更高。然而随着未来电动私家车规模的快速增大，其充电负荷峰值可能超过公交车对应的峰值。计算结果也表明整个电动汽车集群充电高峰发生在夜晚19:00－23:00，负荷峰值可达10.092 7 GW。整个集群在白天8:00－10:00间也有一个小充电高峰，但峰值只有夜间峰值的不到20%。