-
由于传统化石燃料储量的不断枯竭和环境污染的严重性，能源短缺和环境污染问题迫在眉睫[1-3]。可再生能源的间歇性和波动性使电网在与用户侧匹配时无法做到实时性，高比例可再生能源的大规模并网加剧了能源供需在时间和空间上的矛盾[4-6]。综合能源系统（Integrated Energy System，IES）具有考虑多种能源互补耦合、充分吸收可再生能源、提高能源利用率等诸多优点，已成为解决上述问题的有效技术之一[7-9]。
目前，关于电氢耦合IES满足供能需求、降低碳排放和提升系统运行经济性等方面已有较多研究[10-11]。文献[12]建立“源-储-荷”两级优化模型，上层规划模型以相对效益最大化为目标，下层规划模型则以发电侧效益最大化为目标，从而确定最优的可控负荷调度和储能设备容量配置，实现最大化的效益和收益提升；文献[13]细化两阶段P2G过程，将阶梯碳交易引入综合能源系统优化调度，提出可调热电比策略，减少了能量多级损耗，提高IES的低碳经济性；文献[14]构建电-热-氢多能互补系统，有效提高能源利用效率的同时实现了运行成本的最小化。然而，现有研究鲜有考虑燃气掺氢方法，未能充分发掘电氢耦合环节的低碳经济潜力。元启发式算法（Metaheuristic Algorithms）通过模拟自然界中的智能行为，解决了传统优化方法难以应对的复杂问题，显著提高了系统的效率、稳定性和经济效益，在IES中的应用具有广泛的前景和实际意义[15]。文献[16]将碳捕集与电转气环节相结合，源荷双侧协同需求响应策略，采用改进麻雀搜索算法验证模型的有效性；文献[17]建立主从博弈双层优化模型，结合改进灰狼算法满足多个主体的利益同时，保证系统的低碳性；文献[18]将生物质发电引入源-荷-储协同综合能源系统中，通过改进旗鱼算法验证所提模型在不同场景下都具有经济性和环保性；文献[19]考虑能源利用效率和经济效益两种指标，以日运行效益和能源利用效率构建优化调度模型，基于多目标鲸鱼算法验证模型的有效性和可行性；文献[20]改进人工蚁群算法提高全局搜索能力，分析多时间尺度下不同装机容量的风光水火蓄联合运行状况。虽然元启发式算法已经在IES优化调度领域广泛应用，但存在优化算法易出现局部最优解、收敛速度慢等问题。
针对上述问题，文章建立了电解槽制氢、氢储能和燃气轮机掺氢动态平衡的IES，以系统总成本最小为目标函数，运用斑翠鸟优化算法（Pied Kingfisher Optimizer，PKO），通过算例分析证明所提模型和方法的有效性。
-
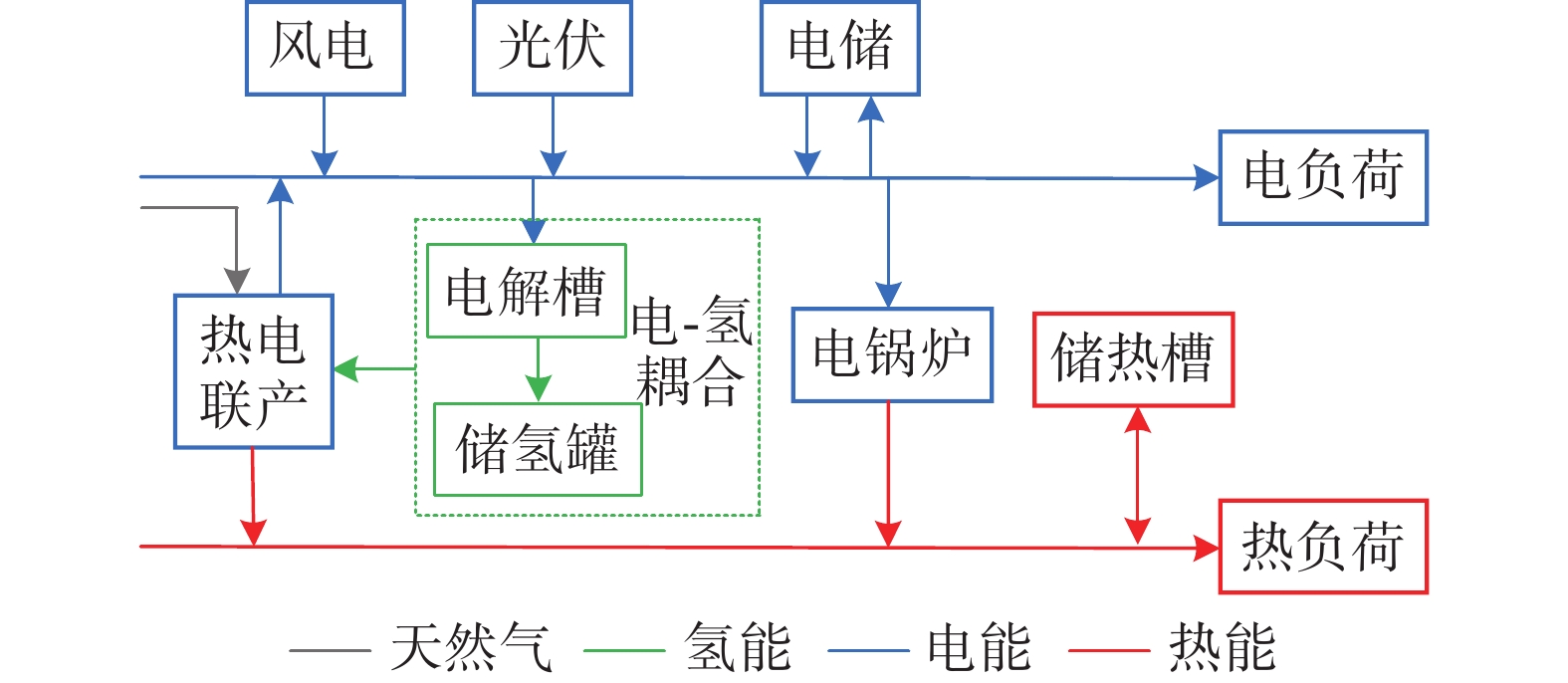
图1给出了含电氢耦合环节的IES框架配置。能源系统中，能源供给侧包括：光伏发电、风力发电。能源转换网络包括：热电联产、电热锅炉、电解槽。储能装置包括：电储能、储氢罐和储热槽。
图 1 综合能源系统框图
Figure 1. Integrated energy system block diagram
-
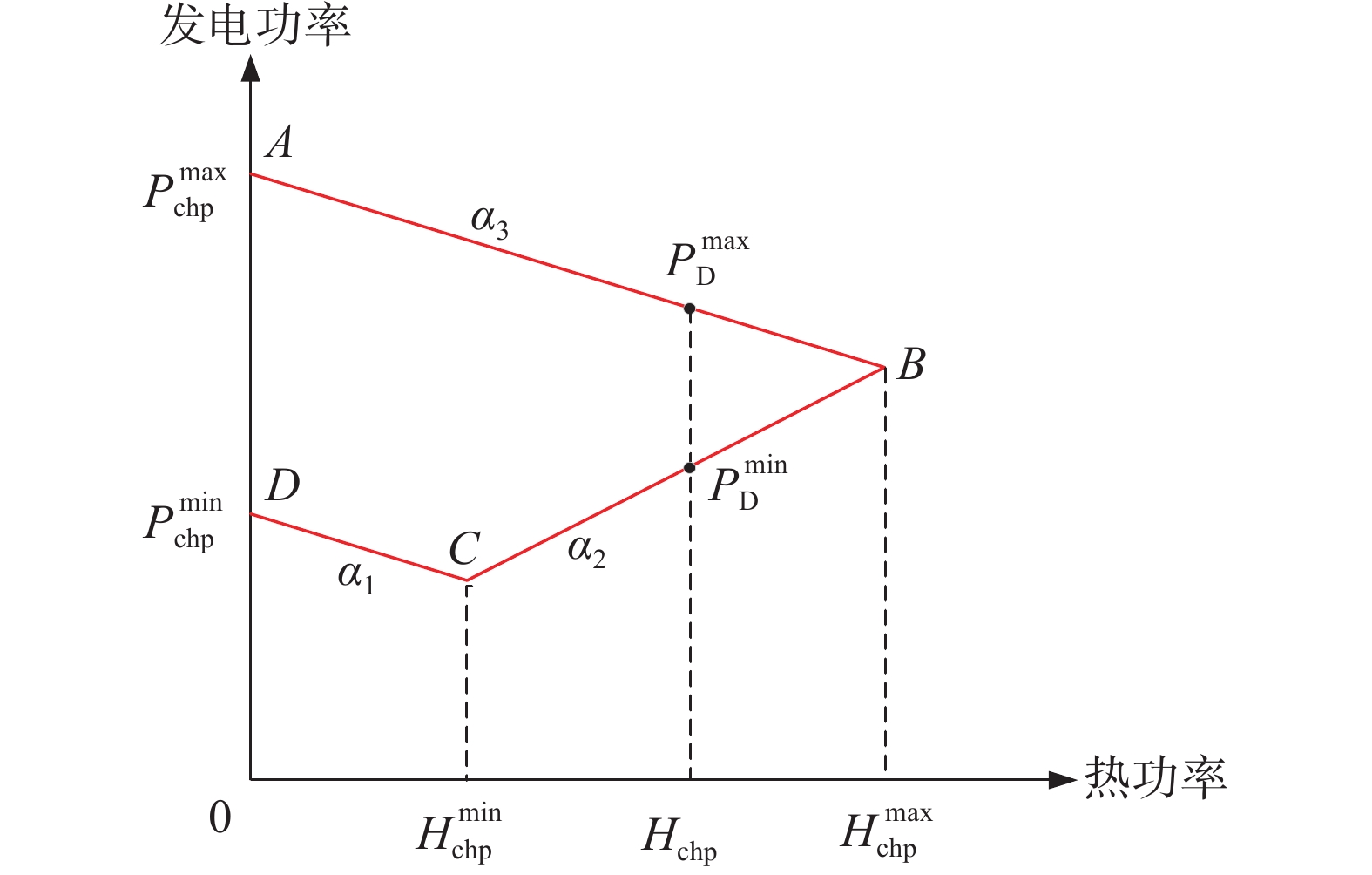
天然气掺氢运行能有效减少设备运行过程中的碳排放量[21]，燃气轮机掺氢比$\phi $（体积分数，下文掺氢比例均为体积分数）在0%～30%vol之间时满足系统回火、燃烧振荡安全等要求[22]。采用掺氢燃气轮机热电联产机组，其运行特性如图2所示，电热出力可调范围由ABCD所构成区域表示[23]。
图 2 燃气轮机热电特性区间
Figure 2. Gas turbine thermoelectric characteristic range
假设掺氢前后燃气轮机燃料输入热功率不变，此时需要调整混氢天然气的体积流量，调整后热电特性区间不发生变化[24]，其数学模型为：
$$ \left\{ {\begin{array}{*{20}{l}} {{P_{{\mathrm{CHP}}}}(t) = \lambda _{{\mathrm{CHP}}}^{\mathrm{e}}[{P_{{\mathrm{CHP}},{\mathrm{C}}{{\mathrm{H}}_4}}}(t) + {P_{{\mathrm{CHP}},{{\mathrm{H}}_2}}}(t)]} \\ {{H_{{\mathrm{CHP}}}}(t) = \lambda _{{\mathrm{CHP}}}^{\mathrm{h}}[{P_{{\mathrm{CHP}},{\mathrm{C}}{{\mathrm{H}}_4}}}(t) + {P_{{\mathrm{CHP}},{{\mathrm{H}}_2}}}(t)]} \\ {{R_{{\mathrm{CHP}}}}(t) = \dfrac{{\dfrac{{{P_{{\mathrm{CHP}},{{\mathrm{H}}_2}}}(t)}}{{{L_{{{\mathrm{H}}_2}}}}}}}{{\dfrac{{{P_{{\mathrm{CHP}},{\mathrm{C}}{{\mathrm{H}}_4}}}(t)}}{{{L_{{\mathrm{C}}{{\mathrm{H}}_4}}}}} + \dfrac{{{P_{{\mathrm{CHP}},{{\mathrm{H}}_2}}}(t)}}{{{L_{{{\mathrm{H}}_2}}}}}}}} \end{array}} \right. $$ (1) 式中：
PCHP(t) ——热电联产机组t时刻电能输出功率（MW）；
HCHP(t) ——热电联产机组t时刻热能输出功率（MW）；
$ P_{{\mathrm{CHP}},{\mathrm{CH_4}}}(t) $ ——在t时刻输入天然气功率（MW）；
$P_{{\mathrm{CHP}},{\mathrm{H_2}}}(t) $ ——在t时刻输入氢气功率（MW）；
$\lambda _{{\mathrm{CHP}}}^\text{e} $ ——热电联产机组电效率，取值为0.34；
$\lambda _{{\mathrm{CHP}}}^\text{h} $ ——热电联产机组电效率，取值为0.4；
RCHP(t) ——热电联产机组在t时刻的掺氢体积比（%）；
$L_{{\mathrm{CH}}_4 }$ ——天然气的热值，取值为11.06 kWh/m3；
$L_{{\mathrm{H}}_2} $ ——氢气的热值，取值为3.6 kWh/m3 [22]。
-
电解槽电解水产氢的体积[25]可表示为：
$$ V_{t{\text{,}}{{\text{H}}_{\text{2}}}}^{{\mathrm{el}}} = \dfrac{{{\eta ^{{\mathrm{el}}}}P_t^{{\mathrm{el}}}}}{{{q_{{{\text{H}}_{\text{2}}}}}}} $$ (2) 式中：
$V_{t{\text{,}}{{\text{H}}_{\text{2}}}}^{{\mathrm{el}}} $ ——电解槽t时刻产生氢气的体积流量（m3）；
ηel ——电解槽制氢效率，取值为0.74[26]；
$ P_{{t}}^{{\mathrm{el}}} $ ——电解槽t时刻消耗的电能功率（MW）。
-
电锅炉功率范围较广，电热效率高[27]。采用电锅炉提高CHP供热时电负荷的灵活性，其数学模型为：
$$ Q_t^{{\mathrm{eb}}} = {\eta ^{{\mathrm{eb}}}}P_t^{{\mathrm{eb}}} $$ (3) 式中：
$ Q_t^{{\mathrm{eb}}} $ ——t时刻电锅炉热出力功率（MW）；
$ P_t^{{\mathrm{eb}}} $ ——t时刻电锅炉输入电能功率（MW）；
ηeb ——电锅炉的热效率。
-
储能设备包括蓄电池、储热槽和储氢罐。其中，蓄电池的数学模型[28]为：
$$ {\mathrm{SOC}}(t) = {\mathrm{SOC}}(t - \Delta t) + \dfrac{{\eta _{}^{{\mathrm{bat}}}P_{t,{\mathrm{ch}}}^{{\mathrm{bat}}}\Delta t}}{{C_{\max }^{{\mathrm{bat}}}}} - \dfrac{{1/\eta _{}^{{\mathrm{bat}}}P{{_{t,{\mathrm{disch}}}^{{\mathrm{bat}}}}_{\text{ }}}\Delta t}}{{C_{\max }^{{\mathrm{bat}}}}} $$ (4) 式中：
$ {\mathrm{SOC}}(t) $ ——t时刻蓄电池的储电状态（%）；
ηbat ——蓄电池的充放电效率（%）；
$P_{t,{\mathrm{ch}}}^{{\mathrm{bat}}} $ ——蓄电池t时刻的充电功率（MW）；
$P_{t,{\mathrm{disch}}}^{{\mathrm{bat}}} $ ——蓄电池t时刻的放电功率（MW）；
${{C_{\max }^{{\mathrm{bat}}}}} $ ——蓄电池的最大容量（MW）。
储热槽数学模型[29]为：
$$ {\mathrm{SOQ}}(t) = {\mathrm{SOQ}}(t - \Delta t) + \dfrac{{\eta _{}^{ts}Q_{t,{\mathrm{ch}}}^{ts}\Delta t}}{{Q_{\max }^{{\mathrm{ts}}}}} - \dfrac{{1/\eta _{}^{ts}Q{{_{t,{\mathrm{disch}}}^{{{ts}}}}_{\text{ }}}\Delta t}}{{Q_{\max }^{{\mathrm{ts}}}}} $$ (5) 式中：
SOQ(t) ——t时刻储热槽储热比例（%）；
ηts ——储热槽的充放热效率（%）；
$ P_{t,{\mathrm{ch}}}^{{\mathrm{ts}}} $ ——储热槽t时刻的吸热功率（MW）；
$ P_{t,{\mathrm{disch}}}^{{\mathrm{ts}}} $ ——储热槽t时刻的放热功率（MW）；
$Q_{{\mathrm{max}}}^{{\mathrm{ts}}} $ ——储热槽的最大容量（MW）。
储氢罐的数学模型[30]为：
$$ {\mathrm{LOH}}(t) = {\mathrm{LOH}}(t - \Delta t) + \dfrac{{V_{t,{{\text{H}}_{\text{2}}}}^{{\mathrm{el}}} - V_{t,{{\text{H}}_{\text{2}}}}^{{\mathrm{chp}}}}}{{S_{\max }^{{\mathrm{hs}}}}}\Delta t $$ (6) 式中：
$ {\mathrm{LOH}}(t) $ ——t时刻储氢罐储氢比例（%）；
$ V_{t,{{\text{H}}_{\text{2}}}}^{{\mathrm{el}}} $ ——电解槽t时刻产生氢气的体积流量（m3）；
$ V_{t,{{\text{H}}_{\text{2}}}}^{{\mathrm{chp}}} $ ——热电联产机组t时刻消耗的氢气体积（m3）；
$ S_{\max }^{{\mathrm{hs}}} $ ——储氢罐的最大容量（m3）。
-
为考虑IES整体经济性，以综合成本最小为目标函数。
$$ \min F = \sum\limits_{t = 1}^T {{F_{{\text{op,}}t}} + F_{{\text{buy,}}t}^{{\mathrm{gas}}} + F_{{\text{buy,}}t}^{\mathrm{e}} + F_{{\text{curt,}}t}^{{\mathrm{pw}}}} + F_t^{\mathrm{h}} $$ (7) 式中：
F ——系统综合成本（元）；
Fop,t ——系统运行成本（元）；
$ {F}_{\mathrm{b}\mathrm{u}\mathrm{y},t}^{\mathrm{g}\mathrm{a}\mathrm{s}} $ ——购气成本（元）；
$ {F}_{\mathrm{b}\mathrm{u}\mathrm{y},t}^{\mathrm{e}} $ ——系统向上级电网购电成本（元）；
$ {F}_{\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t},t}^{\mathrm{p}\mathrm{w}} $ ——弃风弃光成本（元）；
$F_t^{\mathrm{h}} $ ——氢储装置成本（元）；
T ——调度周期。
1）系统运行成本的表达式为：
$$ {F_{{\text{op,}}t}} = F_{{\text{op,}}t}^{{\mathrm{chp}}} + F_{{\text{op,}}t}^{{\mathrm{bat}}} + F_{{\text{op,}}t}^{{\mathrm{ts}}} + F_{{\text{op,}}t}^{{\mathrm{eb}}} $$ (8) 式中：
$ {F}_{\mathrm{o}\mathrm{p},t}^{\mathrm{c}\mathrm{h}\mathrm{p}} $ ——掺氢热电联产机组运行成本（元）；
$ {F}_{\mathrm{o}\mathrm{p},t}^{\mathrm{b}\mathrm{a}\mathrm{t}} $ ——蓄电池组运行成本（元）；
$ {F}_{\mathrm{o}\mathrm{p},t}^{\mathrm{t}\mathrm{s}} $ ——储热槽运行成本（元）；
$ {F}_{\mathrm{o}\mathrm{p},t}^{\mathrm{e}\mathrm{b}} $ ——电锅炉运行成本（元）。
掺氢热电联产机组运行成本：
$$ F_{{\text{op,}}t}^{{\mathrm{chp}}} = \sum\limits_{t = 1}^T {\left[ \begin{gathered} {a_1}\left( {{P_{{\mathrm{chp}}}} + {\alpha _1}{H_{{\mathrm{chp}}}}} \right) + {d_1} \\ {b_1}{\left( {{P_{{\mathrm{chp}}}} + {\alpha _1}{H_{{\mathrm{chp}}}}} \right)^2} + {d_1} \\ \end{gathered} \right]} \Delta t $$ (9) 式中：
a1、b1、d1——热电联产机组成本系数（元/MW）。
蓄电池储能运行成本：
$$ F_{{\text{op,}}t}^{{\mathrm{bat}}} = {a_2}P_{{\mathrm{ch}}}^{{\mathrm{bat}}}(t) + {b_2}P_{{\mathrm{disch}}}^{{\mathrm{bat}}}(t) $$ (10) 式中：
a2、b2——蓄电池充放电成本系数（元/MW）。
储热槽运行成本：
$$ F_{\mathrm{op}, t}^{{\mathrm{t s}}}=a_3 Q_{\mathrm{ch}}^{\mathrm{s}}(t)+b_3 Q_{ \mathrm{dssc}}^{{\mathrm{t s}}}(t) $$ (11) 式中：
a3、b3——单位功率充放成本系数（元/MW）。
电锅炉运行成本：
$$ F_{{\text{op,}}t}^{{\mathrm{eb}}} = {c^{\mathrm{e}}}P_t^{{\mathrm{eb}}} $$ (12) 式中：
ce——分时电价。
2）系统购气成本：
$$ F_{{\text{buy,}}t}^{{\mathrm{gas}}} = {c^{\mathrm{g}}}V_{{\text{C}}{{\text{H}}_{\text{4}}},t}^{{\mathrm{sys}}} $$ (13) 式中：
$ V_{{\text{C}}{{\text{H}}_{\text{4}}},t}^{{\mathrm{sys}}} $——IES在t时刻的耗气量（m3）。
3）系统购电成本：
$$ F_{{\text{buy,}}t}^{\mathrm{e}} = {c^{\mathrm{e}}}P_{{\text{buy}},t}^{{\mathrm{sys}}} $$ (14) 式中：
$ {P}_{\mathrm{b}\mathrm{u}\mathrm{y},t}^{\mathrm{s}\mathrm{y}\mathrm{s}} $——IES在t时刻的购电量（MW）。
4）弃风弃光惩罚成本：
$$ F_{{\text{curt,}}t}^{{\mathrm{pw}}} = {c^{{\mathrm{pw}}}}P_{{\text{curt}},t}^{{\mathrm{pw}}} $$ (15) 式中：
cpw ——弃风弃光惩罚成本系数（元/MW）；
$ {P}_{\mathrm{c}\mathrm{u}\mathrm{r}\mathrm{t},t}^{\mathrm{p}\mathrm{w}} $ ——系统t时刻弃风弃光功率（MW）。
5）氢储装置成本：
$$ C_{{\text{inv}},t}^{\mathrm{h}} = \dfrac{{r{{(1 + r)}^n}}}{{{{(1 + r)}^n} - 1}}\left( {\dfrac{{c_{{\text{inv}}}^{{\mathrm{el}}}P_{{\text{max}}}^{{\mathrm{el}}} + c_{{\text{inv}}}^{{\mathrm{hs}}}P_{{\text{max}}}^{{\mathrm{hs}}}}}{{{T_{\mathrm{a}}}}}} \right) $$ (16) $$ C_{{\text{o\;\& m}},t}^{\mathrm{h}} = {a_4}C_{{\text{inv}},t}^{\mathrm{h}} $$ (17) $$ F_t^{\mathrm{h}} = C_{{\text{inv}},t}^{\mathrm{h}} + C_{{\text{o\;\& m}},t}^{\mathrm{h}} $$ (18) 式中：
$C_{{\text{inv}},t}^{\mathrm{h}} $ ——氢储能的投资成本（元）；
r ——投资回收率（%）；
n ——设备使用年限（a）；
$C_{{\text{inv}}}^{{\mathrm{el}}} $ ——电解槽的单位投资成本系数（元/MW）；
$c_{{\text{inv}}}^{{\mathrm{hs}}} $ ——储氢罐的单位投资成本系数（元/MW）；
$P_{{\text{max}}}^{{\mathrm{el}}} $ ——电解槽的最大功率（MW）；
$P_{{\text{max}}}^{{\mathrm{hs}}} $ ——储氢罐的最大容量（MW）；
Ta ——年运行小时数（h）；
$C_{{\text{o\;\& m}},t}^{\mathrm{h}} $ ——氢储能的运行成本（元）；
a4 ——运维成本比（%）。
-
1）风光发电约束：
$$ 0 \leqslant {P_{{{\mathrm{wt}}}}}(t) \leqslant P_{{{\mathrm{wt}}}}^{\max };0 \leqslant {P_{{{\mathrm{pv}}}}}(t) \leqslant P_{{{\mathrm{pv}}}}^{\max } $$ (19) 式中：
Pwt（t） ——t时刻风电机组的输出功率（MW）；
Ppv（t） ——t时刻光伏机组的输出功率（MW）；
$ P_{{{\mathrm{pv}}}}^{\max } $ ——t时刻风电机组的输出功率上限（MW）；
$P_{{{\mathrm{pv}}}}^{\max } $ ——t时刻光伏机组的输出功率上限（MW）。
2）系统功率平衡约束：
电功率平衡：
$$ \begin{gathered} P_{{\text{buy}},t}^{{\mathrm{sys}}} + P_{{\mathrm{disch}}}^{{\mathrm{bat}}}(t) + {P_{{{\mathrm{wt}}}}}(t) + {P_{{{\mathrm{pv}}}}}(t) + {P_{{\mathrm{chp}}}}(t) + P_{{\mathrm{HFC}}}^{\mathrm{e}}(t)= \\ P_{{{\mathrm{load}}}}^{{\mathrm{e}}}(t) + P_t^{{\mathrm{el}}} + P_{{\mathrm{ch}}}^{{\mathrm{bat}}}(t) \\ \end{gathered} $$ (20) 式中：
$ P_{{{\mathrm{load}}}}^{{\mathrm{e}}}(t) $——IES在t时刻的电负荷（MW）。
热功率平衡：
$$ P_{\mathrm{HFC}}^{\mathrm{h}}(t)+H_{\text {chp }}(t)+Q_{\text {disch }}^{\mathrm{s}}(t)=P_{\text {load }}^{\mathrm{h}}(t)+Q_{\text {ch}}^{{\mathrm{ts}}}(t) $$ (21) 式中：
$ P_{\text {load }}^{\mathrm{h}}(t) $——IES在t时刻的热负荷（MW）。
3）热电联产机组电热耦合约束
$$ 0 \leqslant H_t^{{\mathrm{chp}}} \leqslant H_{\max }^{{\mathrm{chp}}} $$ (22) $$ \begin{gathered} \max \left\{ {{\alpha _1}H_t^{{\mathrm{chp}}} + P_{\min }^{{\mathrm{chp}}},{\alpha _2}H_t^{{\mathrm{chp}}} + {\beta _2}} \right\} \leqslant \\ P_t^{{\mathrm{chp}}} \leqslant {\alpha _3}H_t^{{\mathrm{chp}}} + P_{\max }^{{\mathrm{chp}}} \\ \end{gathered} $$ (23) 式中：
α1 ——最小电出力对应的α值；
α3 ——最大电出力下对应的α值；
α2 ——背压曲线的斜率；
β2 ——背压曲线的截距。
4）电锅炉出力约束
$$ 0 \leqslant Q_t^{{\mathrm{eb}}} \leqslant Q_{\max }^{{\mathrm{eb}}} $$ (24) 式中：
$ Q_{\max }^{{\mathrm{eb}}} $——电锅炉的最大功率（MW）。
5）电池储能约束
$$ {\mathrm{SO}}{{\mathrm{C}}_{\min }} \leqslant {\mathrm{SOC}}(t) \leqslant {\mathrm{SO}}{{\mathrm{C}}_{\max }} $$ (25) $$ 0 \leqslant P_{{\mathrm{ch,t}}}^{{\mathrm{bat}}} \leqslant P_{{\mathrm{ch}},\max }^{{\mathrm{bat}}} $$ (26) $$ 0 \leqslant P_{{\mathrm{disch,t}}}^{{\mathrm{bat}}} \leqslant P_{{\mathrm{disch}},\max }^{{\mathrm{bat}}} $$ (27) 式中：
SOCmax ——蓄电池荷电状态的最大值（%）；
SOCmin ——蓄电池荷电状态的最小值（%）；
$P_{{\mathrm{ch}},\max }^{{\mathrm{bat}}} $ ——蓄电池的最大充电功率（MW）；
$P_{{\mathrm{disch}},\max }^{{\mathrm{bat}}} $ ——蓄电池的最大放电功率（MW）；
储热槽约束与蓄电池约束类似，不再赘述。
6）电氢气耦合约束
$$ 0 \leqslant {\mathrm{LOH}}(t) \leqslant {\mathrm{LO}}{{\mathrm{H}}_{\max }} $$ (28) $$ P_{\min }^{{\mathrm{el}}} \leqslant P_t^{{\mathrm{el}}} \leqslant P_{\max }^{{\mathrm{el}}} $$ (29) $$ V_{{{\text{H}}_{\text{2}}},\min }^{{\mathrm{el}}} \leqslant V_{{{\text{H}}_{\text{2}}},t}^{{\mathrm{el}}} \leqslant V_{{{\text{H}}_{\text{2}}},\max }^{{\mathrm{el}}} $$ (30) 式中：
LOHmax ——最大容量比例（%）；
$P_{\min }^{{\mathrm{el}}} $ ——电解槽最小耗电功率（MW）；
$P_{\max }^{{\mathrm{el}}} $ ——电解槽最大耗电功率（MW）；
$V_{{{\text{H}}_{\text{2}}},{\mathrm{mix}} }^{{\mathrm{el}}} $ ——电解槽最小产氢速率（m3/h）；
$V_{{{\text{H}}_{\text{2}}},\max }^{{\mathrm{el}}} $ ——电解槽最大产氢速率（m3/h）。
-
斑翠鸟优化算法（Pied Kingfisher Optimizer，PKO）灵感来源于自然界中斑翠鸟独特的狩猎行为和共生关系[31]。首先该算法通过空间随机生成一组起始解作为第一次尝试来启动搜索过程：
$$ \begin{gathered} {X_{{\mathrm{i,j}}}} = {\mathrm{LB}} + ({\mathrm{UB}} - {\mathrm{LB}}) \times {r_1} \\ i = 1,2,...,N\begin{array}{*{20}{l}} {} \end{array}{\mathrm{and}}\begin{array}{*{20}{l}} {} \end{array}j = 1,2,...,{\mathrm{Dim}} \\ \end{gathered} $$ (31) 式中：
Xi,j ——第i个个体在第j维的位置；
r1 ——0～1的随机值；
UB、LB ——搜索范围的上下边界；
N ——总体规模；
Dim ——问题总维度。
探索阶段（Rand<0.8）：PKO的探索阶段灵感来自于斑翠鸟的栖息和悬停行为。在其自然栖息地对斑翠鸟的观察表明，它们根据各种因素，在栖息和悬停位置之间交替进行攻击。在PKO中，搜索种群的位置是根据斑翠鸟的觅食活动来确定的。种群位置根据以下公式更新：
$$ \begin{gathered} \left\{ {\begin{array}{*{20}{c}} {{X_i}({s} + 1) = {X_i}({s}) + \alpha \cdot T \times ({X_j}({s}) - {X_i}({s}));} \\ {\alpha = 2{\mu _1} - 1;} \end{array}} \right. \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}i,j = 1,2,...,N\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {} \end{array}{\mathrm{and}}} \end{array}\begin{array}{*{20}{l}} {} \end{array}j \ne i \\ \end{gathered} $$ (32) 式中：
Xi(s+1) ——下一代迭代的解；
Xi(s) ——当前迭代的位置；
T ——状态参数；
α ——随机指向参数；
μ1 ——1～Dim内正态分布随机值。
1）栖息策略（Rand>0.5）：斑翠鸟在栖息地寻找猎物时会保持垂直角度的羽冠，有助于扩大视野；一旦发现了潜在的猎物，斑翠鸟就会降低头冠，利用双目视觉聚焦，并做出精确的动作来捕捉猎物。栖息策略中T值的表达式为：
$$ T = \left(\ln (1) - \ln {\left(\dfrac{{s - 1}}{{{S_{\max }}}}\right)^{\tfrac{1}{{\mathrm{a}}}}}\right) \cos \left(2\pi \cdot {r_1}\right) $$ (33) 式中：
Smax ——最大迭代次数；
a ——常数，值设定为8。
2）悬停策略（Rand<0.5）：斑翠鸟通过高频拍打翅膀，可以在空中保持稳定并进行狩猎。悬停策略中T值的表达式为：
$$ T = {r_1} \left(\dfrac{{{F_j}}}{{{F_i}}}\right) {\left(\dfrac{s}{{{S_{\max }}}}\right)^{\tfrac{1}{{\mathrm{a}}}}} $$ (34) 式中：
Fj、Fi——第j和第i只斑翠鸟的适应度。
开发阶段（Rand≥0.8）：斑翠鸟快速而准确的潜水能力，加上它锋利的喙和出色的视力，使它成为水生环境中有效的捕食者，其数学模型表示为：
$$ \begin{gathered} \left\{ {\begin{array}{*{20}{c}} {{X_i}({s} + 1) = {X_i}({s}) + \phi \cdot o \cdot \alpha \cdot (b - {X_{{\mathrm{best}}}}({s}));} \\ {\phi = {r_1}(\dfrac{{{F_i}}}{{{F_{{\mathrm{best}}}}}});} \\ {o = 2\ln (\dfrac{{ - s}}{{{W_{\max }}}});} \\ {b = {X_i}({s}) + {o^2} \cdot {\mu _2} \cdot {X_{{\mathrm{best}}}}({s})} \end{array}} \right. \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{l}} {} \end{array}\begin{array}{*{20}{c}} {}&{} \end{array}i = 1,2,...,N \\ \end{gathered} $$ (35) 式中：
Φ、ο ——狩猎能力；
b ——适应度影响参数；
Xbest(s) ——当前最佳迭代位置；
Fbest ——在所有迭代中获得的最佳适应度值；
μ2 ——正态分布随机值。
共生阶段（局部逃逸阶段）：斑翠鸟可以捕食水獭惊扰后的鱼类，同时水獭也能从斑翠鸟捕食过程中收益。数学表达式为：
$$ {X_i}({s} + 1) = \left\{ {\begin{array}{*{20}{c}} {{X_m}({s}) + o \cdot \alpha \cdot \left| {{X_i}({s}) - {X_{n}}({s})} \right|}&{{\mathrm{if}} \begin{array}{*{20}{l}} {} \end{array} {\mathrm{Rand}} > (1 - \eta )} \\ {{X_i}({s})}&{{\mathrm{otherwise}}} \end{array}} \right. $$ (36) 式中：
Xm、Xn ——从种群中随机抽取2个个体的位置；
Η ——斑翠鸟的捕食效率，其数学表达式为：
$$ \eta = {\eta _{\max }} - ({\eta _{\max }} - {\eta _{\min }})(\dfrac{s}{{{W_{\max }}}}) $$ (37) 式中：
ηmax、ηmin——斑翠鸟捕食效率的最大、最小值。
-
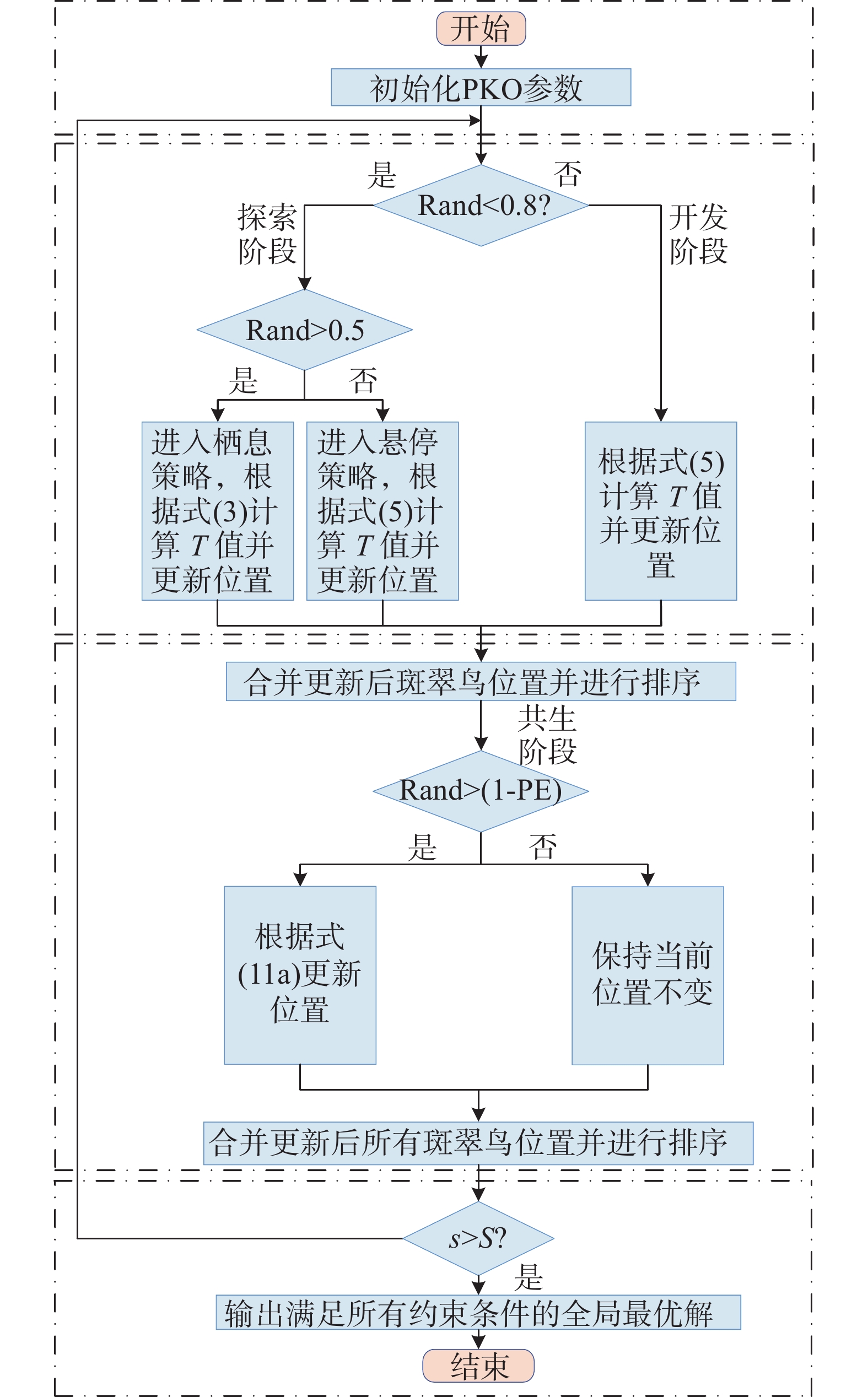
综上，所提算法的流程如图3所示。
图 3 PKO流程图
Figure 3. Flow chart of PKO
Step 1：初始化PKO参数。设置迭代数、种群数量。
Step 2：根据随机因子Rand选择执行探索阶段或者开发阶段。探索阶段种群会进一步根据Rand选择进入栖息或者悬停策略，并更新种群位置，将新种群并进行排序。
Step 3：进入共生阶段后根据随机因子Rand选择是否根据不同迭代公式进行位置更新，并合并更新后的新种群并进行排序。
Step 4：判断是否大于迭代次数，若是，则输出最优可行解，否则返回Step 2。
-
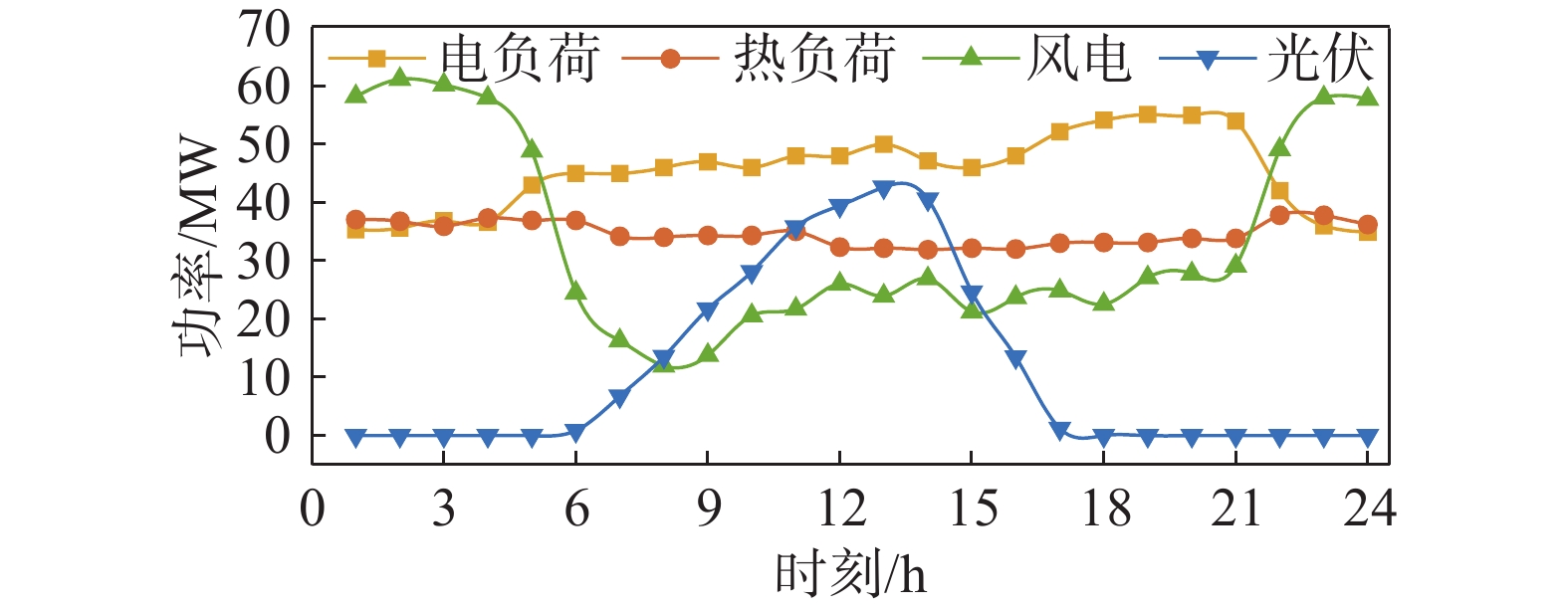
为验证所提模型和方法的有效性，设置仿真算例进行分析，部分仿真参数设置详见文献[8-9，13]，如表1所示。电热负荷及风光等可再生能源预测值作为输入数据详见文献[21]，如图4所示。燃气轮机为“以热定电”模式。
表 1 仿真参数
Table 1. Simulation parameters
参数 数值 参数 数值 $ {\alpha _1} $ －0.15 $ {\alpha _2} $ 0.85 $ {\alpha _3} $ －0.2 Pchp,max/MW 35 Pchp,min/MW 10 Qchp,max/MW 40 Q0/MW 17 a1/(元·MW-1) 13.29 a2/(元·MW-1) 155.42 a3/(元·MW-1) 20 b1/(元·MW-1) 0.025 b2/(元·MW-1) 155.42 b3/(元·MW-1) 20 d1 39 cpw/(元·MW-1) 200 r/% 6 n/a 30 $ P_{\max }^{{\mathrm{el}}} $/MW 15 $ P_{\min }^{{\mathrm{el}}} $/MW 5 $ P_{\max }^{{\mathrm{hs}}} $/MW 10 $ Q_{\max }^{{\mathrm{eb}}} $/MW 10 $ {\beta _2} $ －7 SOCmin 0.3 SOCmax 0.9 LOHmax/MW 20 $ P_{{\mathrm{ch}},\max }^{{\mathrm{bat}}} $/MW 10 
图 4 负荷及风光预测出力
Figure 4. Load and predicted output of wind and solar power
为了验证所提模型和方法的有效性，构建了3种方案进行对比分析。
方案1：在含燃气轮机热电联产的IES调度中，不考虑电氢耦合环节。
方案2：在含燃气轮机热电联产的IES调度中，加入电氢耦合环节，并将掺氢模式设定为固定掺氢，掺氢比为20%。
方案3：在含燃气轮机热电联产的IES调度中，加入电氢耦合环节，并将掺氢模式设定为灵活掺氢，掺氢比范围为0～30%。
-
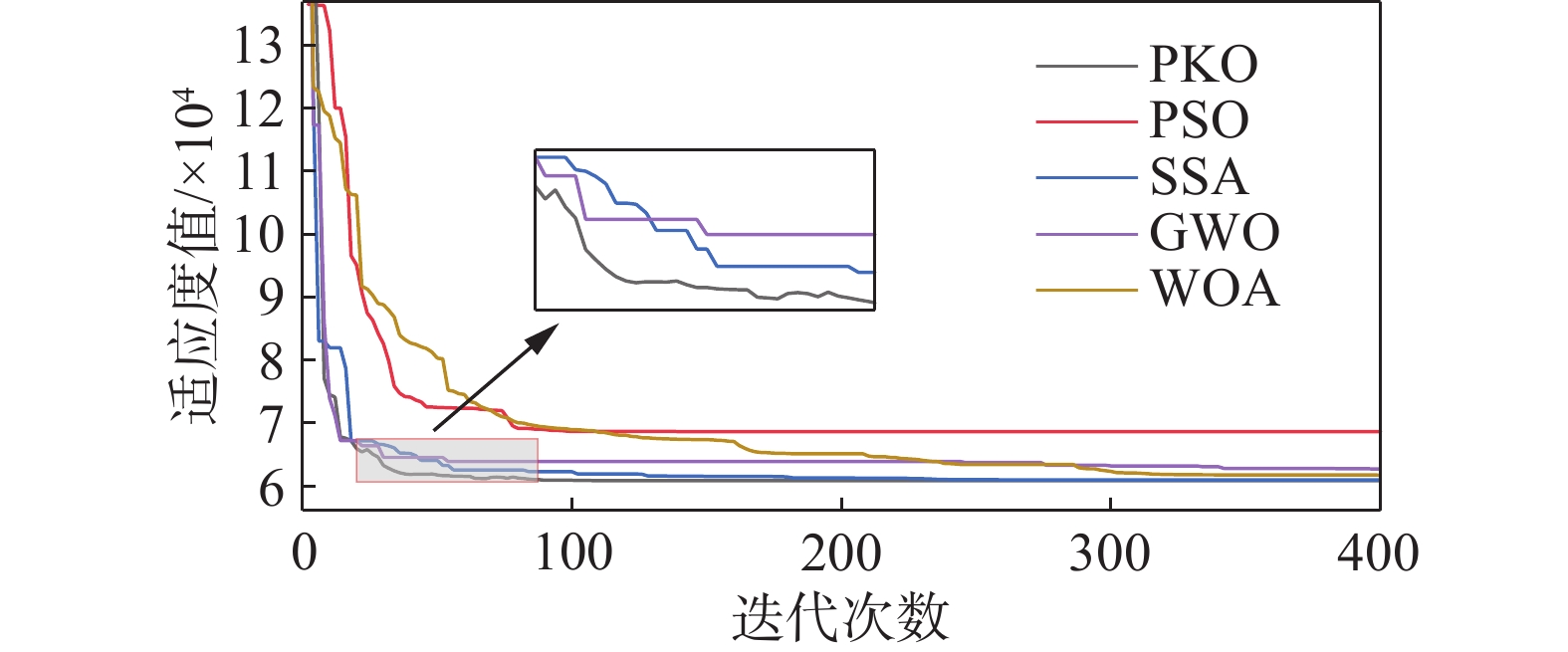
为验证所引进的斑翠鸟算法具有更优的求解性能，文章将PKO、粒子群算法（Particle Swarm Optimization，PSO）、麻雀搜索算法（Sparrow Search Algorithm，SSA）、灰狼优化算法（Grey Wolf Optimization，GWO）以及鲸鱼优化算法（Whale Optimization Algorithm，WOA）优化迭代曲线进行对比分析，结果如图5所示。
图 5 各算法优化迭代曲线
Figure 5. Optimization iteration curves for each algorithm
由图5分析可知，PSO和WOA全局寻优能力较差，在迭代过程中陷入局部最优解，算法求解能力较弱；SSA和GWO虽然最终求解结果接近于最优解，但SSA在200代左右收敛，GWO在350代左右收敛，迭代过程较慢。PKO在迭代初期便向最优解快速接近，在迭代100次左右时收敛于最优解。综上所述，PKO相较于其他4种算法，具有更快的收敛速度，更能达到全局最优解的目标。
-
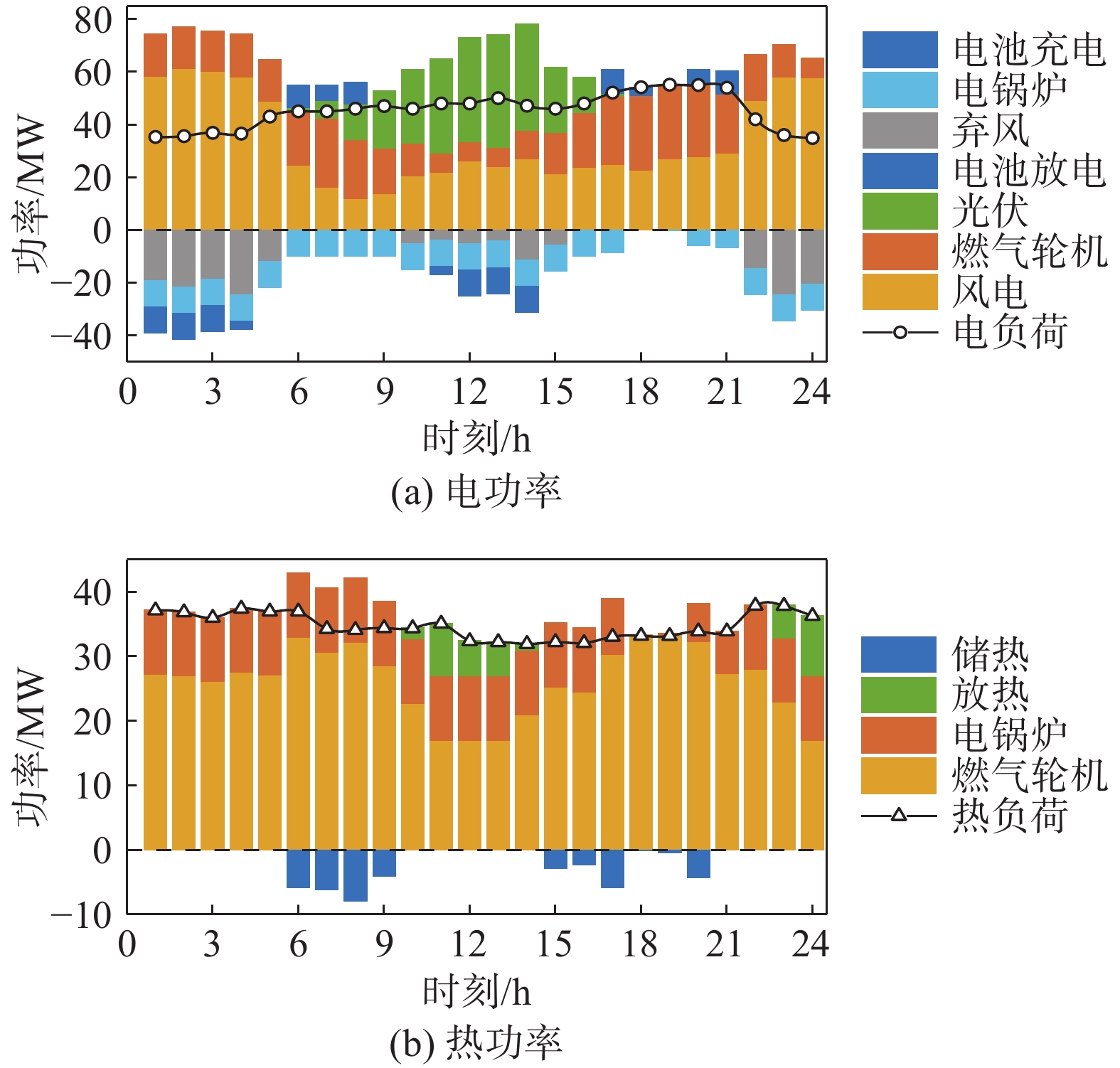
如图6所示，方案1中供应侧主要由燃气轮机和风、光发电组成，负荷侧除常规电负荷外还包含电锅炉以及弃风等。电池与储热槽在全时刻内负荷低谷时进行储能；在负荷高峰时释放电能，实现储能在调度过程中“低储高发”的作用。
图 6 方案1电、热功率平衡
Figure 6. Electric and thermal power balance of scheme 1
由于热电联产具有“以热定电”的特性，夜间热负荷高峰期间，CHP的热出力相对较大，因而导致CHP的电出力也相应提高，导致出现大量弃风现象。
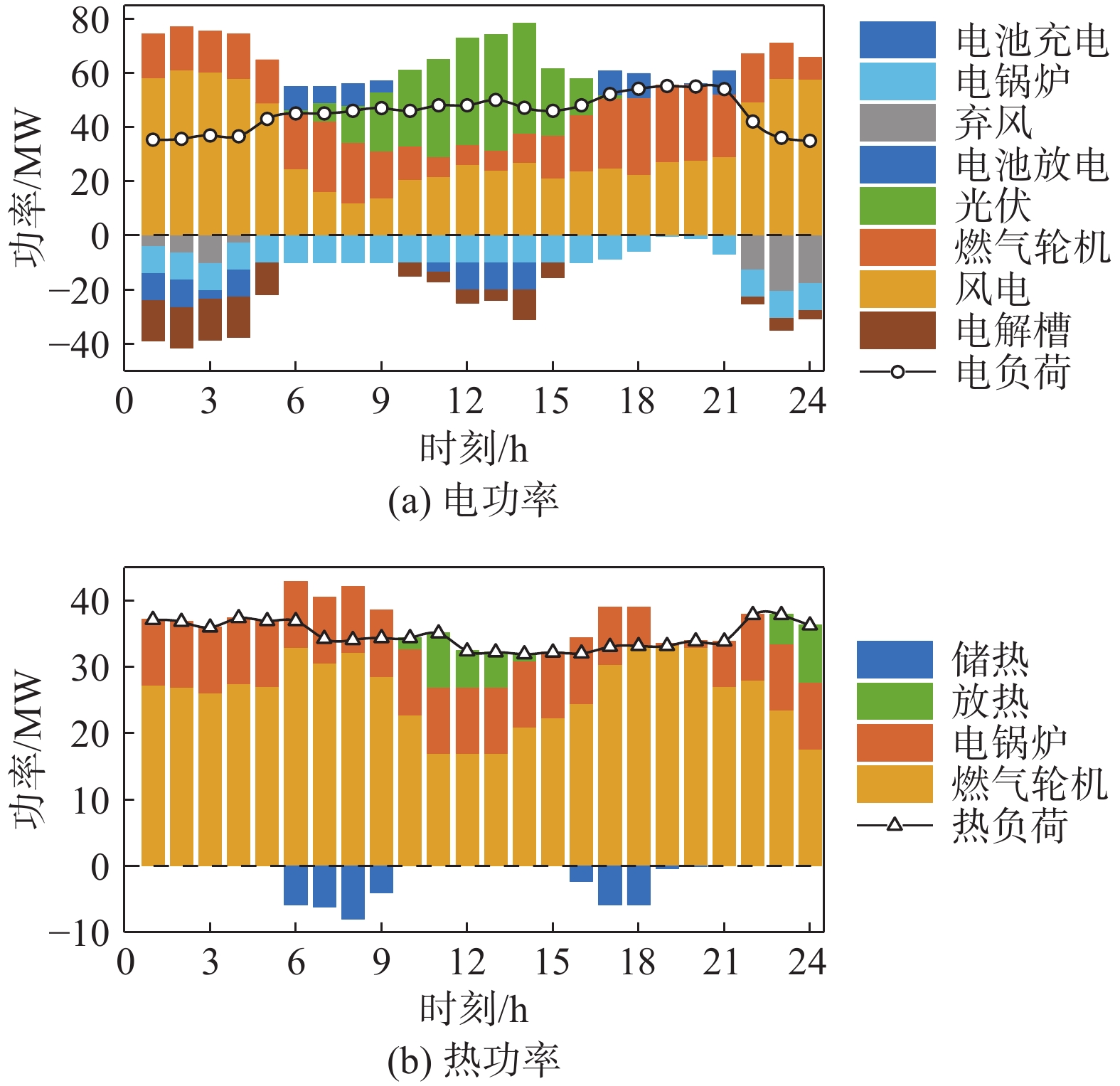
如图7所示，在引入电氢耦合环节后，方案2电解槽出力可以将更多可再生能源消纳，在1:00－15:00时间段内的弃风量大大减少，有效减轻了系统弃风程度；将掺氢燃气轮机引入系统中后，天然气消耗量明显减少。由图7（b）可知，考虑电氢耦合环节后供热在6:00－9:00和16:00－18:00时间段出现两个明显的峰值，储热槽储热过程出现在这两个时间段。
图 7 方案2电、热功率平衡
Figure 7. Electric and thermal power balance of scheme 2
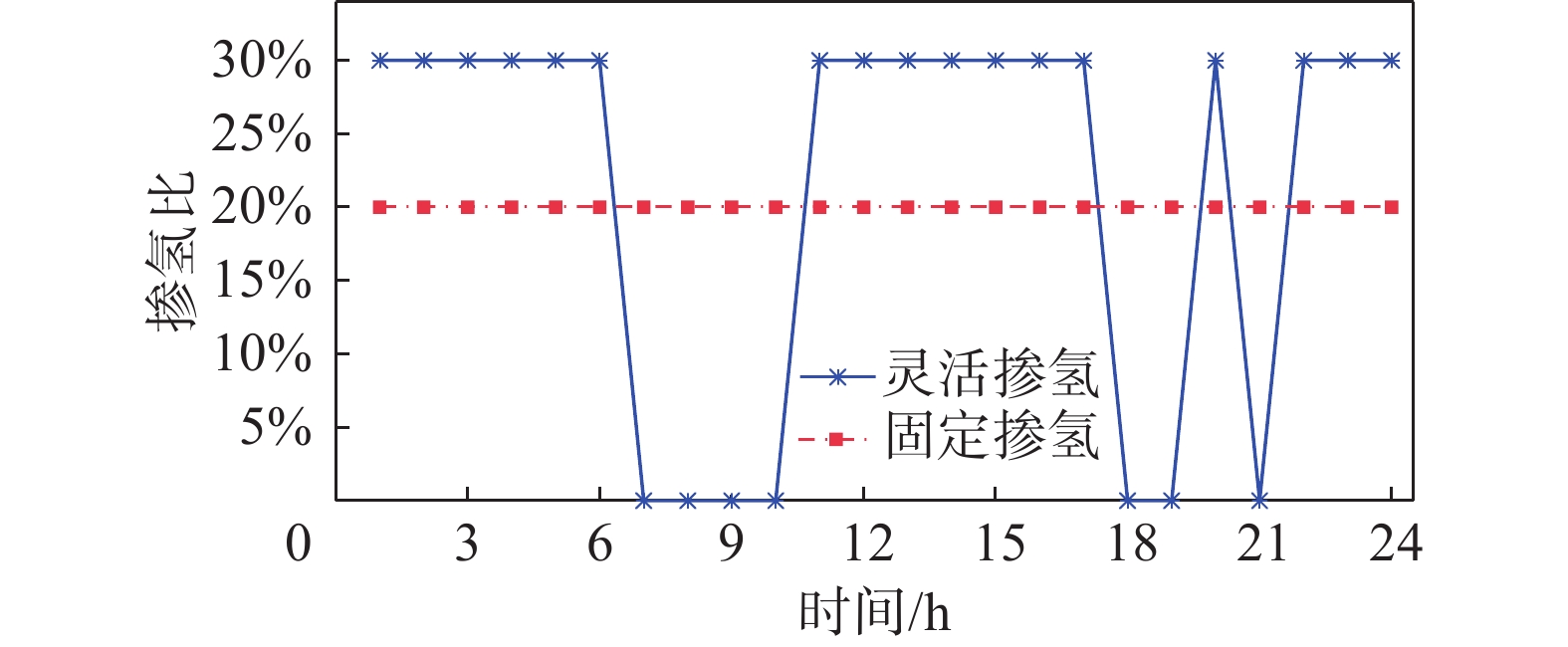
图8所示，相较于方案2，方案3将系统的掺氢模式由固定掺氢变为灵活掺氢模式，提高了IES调度的灵活性，一方面电解槽出力明显增加，系统弃风量降低；另一方面灵活的掺氢比例会使得燃气轮机产生相同的电力和热力的情况下总耗氢量增多，消耗的天然气减少。从调度结果来看，方案3的天然气消耗量较方案2降低了12.43%。
图 8 方案3电、热功率平衡
Figure 8. Electric and thermal power balance of scheme 3
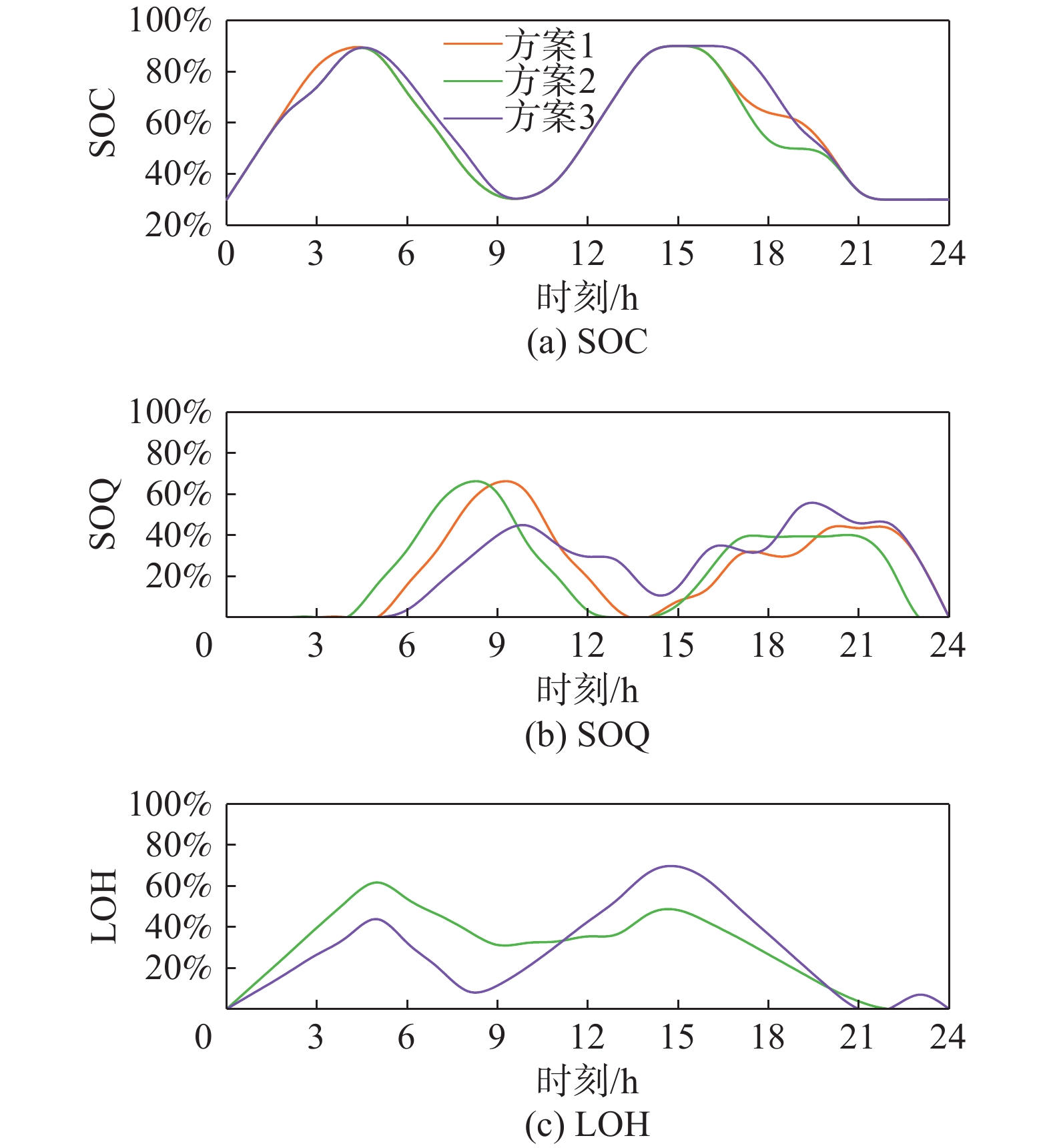
优化调度过程中蓄电池、储氢罐和储热槽等储能设备的工作特性曲线如图9所示。由图9（a）可知，3种方案的蓄电池调度策略均为两个充放周期，电池荷电状态SOC变化主要与电负荷相关，从时间段来看，3种方案的SOC在5:00－10:00和15:00－21:00时间段内从0.9降至0.3，灵活掺氢比例将提高蓄电池的第二个放电周期单位时间内的放电功率。
图 9 储能设备特性曲线
Figure 9. Characteristic curve of energy storage equipment
由图9（b）可知，在13:00－14:00时间段内，方案1和方案2的储热槽荷热量为0，而方案3中储热槽每日能完成一个充放周期，储热槽的利用效率高于方案1和方案2。
由图9（c）可知，方案3相较于方案2的荷氢曲线斜率更大，说明方案3中储氢设备利用水平更高，更能发挥出储能设备“低储高发”的能力；方案2固定燃气轮机的掺氢比例导致储氢罐储氢量在0:00－11:00时间段内高于方案3，在12:00－24:00时间段内受到平衡约束的影响导致电解槽出力减少，储氢罐的储氢水平随之降低。
分析图10中不同曲线的变化趋势可知，在风光出力较大的时间段，方案3中的灵活掺氢模式可提高掺氢比例，增加新能源消纳的同时减少向上级购气成本，达到合理降低系统运行成本的目的；方案2中固定掺氢比例虽然不受能源价格波动的影响，将燃气轮机的掺氢比例固定在同一水平线上，但由于新能源出力的波动性和不确定性，在风光出力较高和负荷需求较低时，高比例掺氢比例会使得系统出现比较大的弃风弃光现象，导致系统经济成本增多。
图 10 不同掺氢模式下掺氢比的变化
Figure 10. Changes in hydrogen blending ratio under different hydrogen blending modes
-
3种不同方案的优化调度成本对比如表2所示。方案3总成本最低，相较于方案1和方案2，总成本分别减少了15.04%和6.99%。分项成本中对总成本减少贡献最大为购气成本，分别减少了23.54%和12.43%，这是由于方案3灵活调节燃气轮机的掺氢比例，使得燃气轮机出力在大于其余两种方案的情况下，燃气轮机的天然气消耗量得到有效减少。
表 2 方案成本对比
Table 2. Comparison of scheme costs
参数 方案1 方案2 方案3 惩罚成本/万元 37 854 14 892 10 139 电池成本/万元 6 545 6 086 5 547 储热槽成本/万元 1 049 972 1 191 电锅炉成本/万元 68 532 69 200 67 195 购气成本/万元 561 550 490 310 429 340 耗氢量/m3 0 30 750 51 461 热电联产运维成本/万元 8 047 8 084 8 961 电解槽成本/万元 0 34 906 58 417 总成本/万元 683 577 624 450 580 791 -
为解决可再生能源的不确定性和不连续性，文章构建了一种含电解水制氢耦合燃气掺氢技术以及氢储的电氢耦合IES，以系统总成本最小为目标，引入斑翠鸟优化算法，提升算法收敛速度，并通过算例分析证明改进算法的优越性：相较于传统燃气轮机，燃气轮机掺氢可提高IES对风光等新能源的消纳能力，方案3相较于方案1和方案2，惩罚成本分别减少73.22%和31.92%；有效降低系统成本和二氧化碳排放量，系统总成本分别减少15.04%和6.99%。改变燃气轮机的掺氢模式将明显影响系统成本。
Optimization and Scheduling of Integrated Energy Systems with Hydrogen-electricity Coupling Based on PKO Algorithm
-
摘要:
目的 在“30·60”双碳的背景下，为解决可再生能源的不确定性和不连续性导致综合能源系统功率平衡性表现不佳的问题。 方法 文章构建含电解水制氢耦合燃气掺氢技术以及氢储的电氢耦合环节，设立了弃风弃光惩罚机制，构建含电氢耦合环节的综合能源系统优化调度模型。针对求解该模型求解时易陷入局部最优和收敛速度慢等问题，引入斑翠鸟优化算法（Pied Kingfisher Optimizer，PKO）。 结果 模型以系统总成本最小为目标函数，求解得到各能源网络机组出力的优化调度结果；PKO与传统优化算法相比，具有更快的收敛速度，更能达到全局最优解的目标。 结论 算例分析表明，所提模型和方法相较于其他方案，总成本分别减少了15.04%和6.99%，有效提高了综合能源系统新能源利用水平，降低了系统总成本，更具经济性。 Abstract:Introduction In the context of the "30·60" carbon peak and neutrality targets, this paper’s purpose is to address the problem of poor power balance performance in integrated energy systems caused by the uncertainty and discontinuity of renewable energy. Method This paper constructed a hydrogen-electricity coupling link that included hydrogen production from electrolyzed water coupled with gas hydrogen blending technology and hydrogen storage, established a punishment mechanism for wind and solar curtailment, and constructed an optimization and scheduling model for integrated energy system that included hydrogen-electricity coupling link. To address the problems of getting stuck in local optima and slow convergence speed during the solution process, the Pied Kingfisher Optimizer (PKO) algorithm was introduced. Result The model aims to minimize the total system cost as the objective function, and solves for the optimal scheduling results of the output of each energy network unit; Compared with traditional optimization algorithms, PKO has a faster convergence speed and is better able to achieve the goal of global optimal solution. Conclusion Case analysis indicates that using the model and method proposed in this paper reduces the total cost by 15.04% and 6.99% respectively compared to other schemes, effectively improving the utilization level of new energy in the integrated energy system, reducing the total system cost, and making it more economical. -
图 10 不同掺氢模式下掺氢比的变化
Fig. 10 Changes in hydrogen blending ratio under different hydrogen blending modes
表 1 仿真参数
Tab. 1. Simulation parameters
参数 数值 参数 数值 $ {\alpha _1} $ －0.15 $ {\alpha _2} $ 0.85 $ {\alpha _3} $ －0.2 Pchp,max/MW 35 Pchp,min/MW 10 Qchp,max/MW 40 Q0/MW 17 a1/(元·MW-1) 13.29 a2/(元·MW-1) 155.42 a3/(元·MW-1) 20 b1/(元·MW-1) 0.025 b2/(元·MW-1) 155.42 b3/(元·MW-1) 20 d1 39 cpw/(元·MW-1) 200 r/% 6 n/a 30 $ P_{\max }^{{\mathrm{el}}} $/MW 15 $ P_{\min }^{{\mathrm{el}}} $/MW 5 $ P_{\max }^{{\mathrm{hs}}} $/MW 10 $ Q_{\max }^{{\mathrm{eb}}} $/MW 10 $ {\beta _2} $ －7 SOCmin 0.3 SOCmax 0.9 LOHmax/MW 20 $ P_{{\mathrm{ch}},\max }^{{\mathrm{bat}}} $/MW 10 
下载: 导出CSV
表 2 方案成本对比
Tab. 2. Comparison of scheme costs
参数 方案1 方案2 方案3 惩罚成本/万元 37 854 14 892 10 139 电池成本/万元 6 545 6 086 5 547 储热槽成本/万元 1 049 972 1 191 电锅炉成本/万元 68 532 69 200 67 195 购气成本/万元 561 550 490 310 429 340 耗氢量/m3 0 30 750 51 461 热电联产运维成本/万元 8 047 8 084 8 961 电解槽成本/万元 0 34 906 58 417 总成本/万元 683 577 624 450 580 791
下载: 导出CSV
-
[1] 李政, 陈思源, 董文娟, 等. 碳约束条件下电力行业低碳转型路径研究 [J]. 中国电机工程学报, 2021, 41(12): 3987-4000. DOI: 10.13334/j.0258-8013.pcsee.210671. LI Z, CHEN S Y, DONG W J, et al. Low carbon transition pathway of power sector under carbon emission constraints [J]. Proceedings of the CSEE, 2021, 41(12): 3987-4000. DOI: 10.13334/j.0258-8013.pcsee.210671. [2] 张尧翔, 刘文颖, 庞清仑, 等. 计及综合需求响应参与消纳受阻新能源的多时间尺度优化调度策略 [J]. 电力建设, 2023, 44(1): 1-11. DOI: 10.12204/j.issn.1000-7229.2023.01.001. ZHANG Y X, LIU W Y, PANG Q L, et al. Multi-timescale trading strategies for the participation of multi-energy demand response in the consumption of blocked new energy sources [J]. Electric power construction, 2023, 44(1): 1-11. DOI: 10.12204/j.issn.1000-7229.2023.01.001. [3] 黎静华, 朱梦姝, 陆悦江, 等. 综合能源系统优化调度综述 [J]. 电网技术, 2021, 45(6): 2256-2269. DOI: 10.13335/j.1000-3673.pst.2021.0020. LI J H, ZHU M S, LU Y J, et al. Review on optimal scheduling of integrated energy systems [J]. Power system technology, 2021, 45(6): 2256-2269. DOI: 10.13335/j.1000-3673.pst.2021.0020. [4] 苏步芸, 王诗超. 新型电力系统背景下新能源送出合理消纳率研究 [J]. 南方能源建设, 2023, 10(6): 43-50. DOI: 10.16516/j.gedi.issn2095-8676.2023.06.005. SU B Y, WANG S C. Research on reasonable consumption rate of new energy transmission under the new power system [J]. Southern energy construction, 2023, 10(6): 43-50. DOI: 10.16516/j.gedi.issn2095-8676.2023.06.005. [5] 曹韵, 韩松, 荣娜, 等. 基于GCTMSA的梯级水火风光蓄储联合调度 [J]. 电力系统保护与控制, 2023, 51(3): 108-116. DOI: 10.19783/j.cnki.pspc.220475. CAO Y, HAN S, RONG N, et al. Dispatch of a cascade hydro-thermal-wind-photovoltaic-storage complementary system based on GCTMSA [J]. Power system protection and control, 2023, 51(3): 108-116. DOI: 10.19783/j.cnki.pspc.220475. [6] SONG Q, RONG N, HAN S, et al. Decarbonization pathways of China's provincial energy systems under carbon constraints: a case study of Guizhou province [J]. Energy reports, 2022, 8: 9363-9378. DOI: 10.1016/j.egyr.2022.07.045. [7] 章雪萌, 孟祥娟, 毛福斌, 等. 考虑多时间尺度的新能源特性对地区电网的影响评估 [J]. 南方能源建设, 2023, 10(5): 166-173. DOI: 10.16516/j.gedi.issn2095-8676.2023.05.020. ZHANG X M, MENG X J, MAO F B, et al. Impact assessment of new energy characteristics on regional power grid considering multiple time scales [J]. Southern energy construction, 2023, 10(5): 166-173. DOI: 10.16516/j.gedi.issn2095-8676.2023.05.020. [8] 葛磊蛟,李京京,李昌禄,等. 面向零碳园区的综合能源系统优化运行技术综述 [J]. 电网技术, 2024, 48(5): 1821-1835. DOI: 10.13335/j.1000-3673.pst.2023.0993. GE L J, LI J J, LI C L, et al. Overview of integrated energy system optimization operation technology for zero carbon parks [J]. Power system technology, 2024, 48(5): 1821-1835. DOI: 10.13335/j.1000-3673.pst.2023.0993. [9] 陈锦涛, 杨苹, 陈滢, 等. 基于综合需求侧响应策略的园区多能源系统优化运行 [J]. 可再生能源, 2021, 39(2): 222-228. DOI: 10.13941/j.cnki.21-1469/tk.2021.02.013. CHEN J T, YANG P, CHEN Y, et al. Optimized operation of multi-energy system in the industrial park based on integrated demand response strategy [J]. Renewable energy resources, 2021, 39(2): 222-228. DOI: 10.13941/j.cnki.21-1469/tk.2021.2.013. DOI: 10.13941/j.cnki.21-1469/tk.2021.02.013. [10] 李永毅, 王子晗, 张磊, 等. 风-光-氢-燃气轮机一体化氢电耦合系统容量配置优化 [J/OL]. 中国电机工程学报, 1-13. (2023-12-28) [2024-07-29]. https://doi.org/10.13334/j.0258-8013.pcsee.232133. LI Y Y, WANG Z H, ZHANG L, et al. Capacity allocation optimization of integrated hydrogen-electric system of wind-solar-hydrogen-gas turbine [J/OL]. Proceedings of the CSEE, 1-13. (2023-12-28) [2024-07-29]. https://doi.org/10.13334/j.0258-8013.pcsee.232133. [11] 李奇, 霍莎莎, 蒲雨辰, 等. 面向含氢综合能源系统的电-碳-氢耦合交易市场研究综述 [J]. 电力自动化设备, 2023, 43(12): 175-187. DOI: 10.16081/j.epae.202310006. LI Q, HUO S S, PU Y C, et al. Review on electricity-carbon-hydrogen coupling trading market for integrated energy system with hydrogen [J]. Electric power automation equipment, 2023, 43(12): 175-187. DOI: 10.16081/j.epae.202310006. [12] 赵蕊, 谭忠富, 德格吉日夫, 等. 计及需求响应的微电网“源-储-荷”两级协调运行优化模型 [J]. 可再生能源, 2019, 37(11): 1630-1636. DOI: 10.13941/j.cnki.21-1469/tk.2019.11.008. ZHAO R, TAN Z F, DEGEJIRIFU, et al. Two-level coordinated operation optimization model of the source-storage-load in microgrid considering demand response [J]. Renewable energy resources, 2019, 37(11): 1630-1636. DOI: 10.13941/j.cnki.21-1469/tk.2019.11.008. [13] 陈锦鹏, 胡志坚, 陈颖光, 等. 考虑阶梯式碳交易机制与电制氢的综合能源系统热电优化 [J]. 电力自动化设备, 2021, 41(9): 48-55. DOI: 10.16081/j.epae.202109032. CHEN J P, HU Z J, CHEN Y G, et al. Thermoelectric optimization of integrated energy system considering ladder-type carbon trading mechanism and electric hydrogen production [J]. Electric power automation equipment, 2021, 41(9): 48-55. DOI: 10.16081/j.epae.202109032. [14] WU X, QI S X, WANG Z, et al. Optimal scheduling for microgrids with hydrogen fueling stations considering uncertainty using data-driven approach [J]. Applied energy, 2019, 253: 113568. DOI: 10.1016/j.apenergy.2019.113568. [15] LUIZ JUNHO PEREIRA J, OLIVER G A, BRENDON FRANCISCO M, et al. Multi-objective lichtenberg algorithm: a hybrid physics-based meta-heuristic for solving engineering problems [J]. Expert systems with applications, 2022, 187: 115939. DOI: 10.1016/j.eswa.2021.115939. [16] 李泽霜, 唐忠, 程卓, 等. 基于改进麻雀搜索算法的电-热-气-氢综合能源系统优化 [J/OL]. 现代电力, 2023: 1-11. (2023-10-17) [2024-07-19]. https://doi.org/10.19725/j.cnki.1007-2322.2022.0351. LI Z S, TANG Z, CHENG Z, et al. Optimization of electric-heat-gas-hydrogen integrated energy system based on improved sparrow search algorithm [J/OL]. Modern electric power, 2023: 1-11. (2023-10-17) [2024-07-19]. https://doi.org/10.19725/j.cnki.1007-2322.2022.0351. [17] 关红伟, 刘丽娟, 白牧可, 等. 多主体博弈下基于改进灰狼算法的综合能源服务商优化运行策略 [J]. 电力系统及其自动化学报, 2024, 36(7): 78-85. DOI: 10.19635/j.cnki.csu-epsa.001343. GUAN H W, LIU L J, BAI M K, et al. Optimized operation strategy for integrated energy service provider based on improved grey wolf optimization algorithm in multi-agent game [J]. Proceedings of the CSU-EPSA, 2024, 36(7): 78-85. DOI: 10.19635/j.cnki.csu-epsa.001343. [18] 张政林, 张惠娟, 孙文治, 等. 基于改进旗鱼算法的综合能源系统能量管理 [J]. 电力系统保护与控制, 2022, 50(22): 142-151. DOI: 10.19783/j.cnki.pspc.220006. ZHANG Z L, ZHANG H J, SUN W Z, et al. Energy management of an integrated energy system based on an improved sailed fish optimizer algorithm [J]. Power system protection and control, 2022, 50(22): 142-151. DOI: 10.19783/j.cnki.pspc.220006. [19] 韩永明, 王新鲁, 耿志强, 等. 基于AMOWOA的区域综合能源系统运行优化调度 [J]. 自动化学报, 2024, 50(3): 576-588. DOI: 10.16383/j.aas.c211146. HAN Y M, WANG X L, GENG Z Q, et al. Optimal scheduling for regional integrated energy system operation based on the AMOWOA [J]. Acta automatica sinica, 2024, 50(3): 576-588. DOI: 10.16383/j.aas.com211146. DOI: 10.16383/j.aas.c211146. [20] 朱宏毅, 杨昌海, 沈渭程, 等. 基于改进免疫蚁群算法的风光水火蓄多源互补优化调度 [J]. 电网与清洁能源, 2023, 39(10): 129-136. DOI: 10.3969/j.issn.1674-3814.2023.10.016. ZHU H Y, YANG C H, SHEN W C, et al. A study on the multi-source complementary optimized scheduling of wind-photovoltaic-hydro-thermal-pumped based on improved immune ant colony algorithm [J]. Power system and clean energy, 2023, 39(10): 129-136. DOI: 10.3969/j.issn.1674-3814.2023.10.016. [21] 崔杨, 闫石, 仲悟之, 等. 含电转气的区域综合能源系统热电优化调度 [J]. 电网技术, 2020, 44(11): 4254-4263. DOI: 10.13335/j.1000-3673.pst.2019.2468. CUI Y, YAN S, ZHONG W Z, et al. Optimal thermoelectric dispatching of regional integrated energy system with power-to-gas [J]. Power system technology, 2020, 44(11): 4254-4263. DOI: 10.13335/j.1000-3673.pst.2019.2468. [22] 李立新, 刘星雨, 曾过房, 等. SGT-800重型燃气轮机天然气掺氢燃烧数值模拟研究 [J]. 热力发电, 2023, 52(12): 70-78. DOI: 10.19666/j.rlfd.202303033. LI L X, LIU X Y, ZENG G F, et al. Numerical modeling of natural gas combustion with hydrogen blending in SGT-800 heavy-duty gas turbine [J]. Thermal power generation, 2023, 52(12): 70-78. DOI: 10.19666/j.rlfd.202303033. [23] NAZARI-HERIS M, MOHAMMADI-IVATLOO B, ASADI S, et al. Large-scale combined heat and power economic dispatch using a novel multi-player harmony search method [J]. Applied thermal engineering, 2019, 154: 493-504. DOI: 10.1016/j.applthermaleng.2019.03.095. [24] 李小龙, 洪小飞, 陈宇卿. 燃气轮机掺氢燃烧技术 [J]. 南方能源建设, 2023, 10(6): 14-25. DOI: 10.16516/j.gedi.issn2095-8676.2023.06.002. LI X L, HONG X F, CHEN Y Q. Hydrogen-blended combustion technology in gas turbine [J]. Southern energy construction, 2023, 10(6): 14-25. DOI: 10.16516/j.gedi.issn2095-8676.2023.06.002. [25] 朱兰, 王吉, 唐陇军, 等. 计及电转气精细化模型的综合能源系统鲁棒随机优化调度 [J]. 电网技术, 2019, 43(1): 116-126. DOI: 10.13335/j.1000-3673.pst.2018.1895. ZHU L, WANG J, TANG L J, et al. Robust stochastic optimal dispatching of integrated energy systems considering refined power-to-gas model [J]. Power system technology, 2019, 43(1): 116-126. DOI: 10.13335/j.1000-3673.pst.2018.1895. [26] 刘晓军, 聂凡杰, 杨冬锋, 等. 碳捕集电厂-电转气联合运行模式下考虑绿证-碳交易机制的综合能源系统低碳经济调度 [J]. 电网技术, 2023, 47(6): 2207-2217. DOI: 10.13335/j.1000-3673.pst.2022.1507. LIU X J, NIE F J, YANG D F, et al. Low carbon economic dispatch of integrated energy systems considering green certificates-carbon trading mechanism under CCPP-P2G joint operation model [J]. Power system technology, 2023, 47(6): 2207-2217. DOI: 10.13335/j.1000-3673.pst.2022.1507. [27] 郭宬昊, 谢子硕, 王金星, 等. 新能源系统中双储能耦合燃煤机组的应用策略研究 [J]. 南方能源建设, 2022, 9(3): 62-71. DOI: 10.16516/j.gedi.issn2095-8676.2022.03.007. GUO C H, XIE Z S, WANG J X, et al. Research on operation strategy of the application of dual energy storage coupled with coal-fired units in new energy power system [J]. Southern energy construction, 2022, 9(3): 62-71. DOI: 10.16516/j.gedi.issn2095-8676.2022.03.007. [28] ADEFARATI T, BANSAL R C, BETTAYEB M, et al. Optimal energy management of a PV-WTG-BSS-DG microgrid system [J]. Energy, 2021, 217: 119358. DOI: 10.1016/j.energy.2020.119358. [29] 崔杨, 谷春池, 付小标, 等. 考虑广义电热需求响应的含碳捕集电厂综合能源系统低碳经济调度 [J]. 中国电机工程学报, 2022, 42(23): 8431-8445. DOI: 10.13334/j.0258-8013.pcsee.211942. CUI Y, GU C C, FU X B, et al. Low-carbon economic dispatch of integrated energy system with carbon capture power plants considering generalized electric heating demand response [J]. Proceedings of the CSEE, 2022, 42(23): 8431-8445. DOI: 10.13334/j.0258-8013.pcsee.211942. [30] LUCAS A, NETO R C, SILVA C A. Energy supply infrastructure LCA model for electric and hydrogen transportation systems [J]. Energy, 2013, 56: 70-80. DOI: 10.1016/j.energy.2013.04.056. [31] BOUAOUDA A, HASHIM F A, SAYOUTI Y, et al. Pied kingfisher optimizer: a new bio-inspired algorithm for solving numerical optimization and industrial engineering problems [J]. Neural computing and applications, 2024, 36(25): 15455-15513. DOI: 10.1007/s00521-024-09879-5. -
点击查看大图
图(10) / 表 (2)
计量
- 文章访问数: 2008
- HTML全文浏览量: 995
- PDF下载量: 4
- 被引次数: 0
