-
现阶段，风能和太阳能具有吸引力，因为它们的低生命周期排放具有更广泛的环境效益[1]。湍流风环境给风场的不规则性和动态性带来的影响，会导致多风机发电系统的功率输出产生波动，受到工程界的广泛关注。
大型风电场建设是现今风力发电产业发展的趋势，可以增加风力发电的效率。但是实际情况表明，风机的个数与风力发电的效率并不成正比，其中的主要原因就是风电场中存在尾流效应[2]。风力发电机运行过程中会提取来流风的动能并将其转化为风力发电机输出功率，造成风轮平面后的风速显著降低、湍流强度增大，从而形成十分明显的尾流区域。处于尾流区域中的风力发电机的气动功率及气动载荷将会受到不利影响[3]。在双风机的串联分布情况下，下游风机受到上游风机的尾流影响，下游风机的发电功率会减少60%[4]。因此，对风电场中风机机位合理布置以减小尾流效应成为了现在的研究热点[5]。研究风场中多台风机不同排布方式前，需以单风机周围流场和气动性能作为研究基础。PortéAgel等[6]利用边界层理念，对风机尾流进行了数值模拟，其模拟结果与风洞实验测量结果基本一致；Barthelemie[7-8]利用数值模拟、风洞实验及实地勘测相结合的方法，深入分析了单台风机的气动性能和尾流流场。陈默等[9]指出不同风电场规模下整体输出效能均随风机的纵向间距增大而增大；张周周等[10]通过数值模拟的方法对单列放置的2台风机压力场和涡量场进行了研究，发现当风机间距离增大时，下游风机所受的不利影响随之减小；李少华等[11]采用CFD方法对2台风机尾流进行了研究；田琳琳等[12]采用致动盘模型对多台风机在多种风况条件下风机尾流相互干扰进行了研究，避免了因尾流效应的存在使得风机的输出功率减少。为了提高风电场的发电效率，对风电场内风机进行合理布置，使风电场的经济性达到最佳，开展风机间不同排列方式的研究是很有必要的[13]。通过改变上下游风机横向间距的尾流效应抑制策略受到了大量学者的关注。蔡新等[14]研究发现，风机在串列布置下时，在风机下游5倍直径处仍会受到上游风机的影响，并提出机组阵列布置时可以对风机进行错列；Wu等[15]采用大涡模拟方法，对中性大气边界层单一入流方向布置30排共120台风机，对串列布置及水平错列布置下的各排风机平均输出功率进行对比，研究发现错列布置方式能够更好地提升风电场的输出功率；Zhao等[16]运用数值模拟的方法对2台串列、并列及错列风机进行了研究，发现不同机组间距离与当地盛行风向变化范围成正比；张思瑶等[17]指出3台风机并列布置时，各风力机尾流速度比率基本一致，三风机组在错列布置时，尾流效应对下游风机工作性能影响较小，错列角度越大，尾流损失越小。此外也有许多学者将优化算法应用于风电场布局优化中来。Mosetti等[18]将遗传算法与尾流模型相结合，优化了大型风电场中风机排布问题；Grady等[19]利用Mosetti的优化结果，采用改进遗传算法优化风机排布，得到比Mosetti更优结果；徐佳楠等[20]提出一种自适应权重的遗传——粒子群优化算法，对风机群的排布进行了优化。
现有论文主要根据经验值来确定风电场中风机的布局及排列，而且大多是分析当改变风机间距时，上游风机对下游单风机的影响，并未将风机间距离的改变对后排多风机带来的影响进行细致研究，也未将风机间横向间距与纵向间距相结合。文章研究了湍流风场中3台NREL 5 MW风机在横向距离以及纵向距离改变时对于风电场总功率的影响；对横向间距及纵向间距进行了更为细致的划分；通过改变风机间距得到后2台风机功率情况，分析了风机间距对风电场总功率及其提升率的影响。
-
风机是将风能转化为机械能的一种装置。当空气通过风机时，风的能量驱动叶片旋转，空气的部分动能被转化为机械能，空气在风机叶片上游和下游的运动随之改变。风机的动量理论为这一动态过程提供了解释。风机的叶片所受力与风速成正比，流动过程中的能量损失也表现为下游风速的下降。这表明空气的部分动能在整个流动过程中被转化成了机械能。研究将基于以下3种假设：（1）气流为不可压缩的均匀定常流；（2）风轮简化为一忽略摩擦力的桨盘；（3）风轮前后方气流静压不变，且推力沿风轮轮面均匀分布。空气在流过风轮时的动量变化过程可描述为：空气在穿过桨盘时受到阻力导致风速不断的衰减，直到在远离桨盘的位置时不受阻力的作用，风速趋于稳定。在这一系列过程中，马赫数一直很小，因此假定空气密度基本不变为常量，因为穿过桨盘的气体是连续的，所以桨盘上下游的气体质量、流量相等，根据质量守恒定律可得：
$$ \rho A_\infty U_\infty = \rho A_{\mathrm{d}}U_{\mathrm{d}} = \rho A_{\mathrm{w}}U_{\mathrm{w}} $$ (1) 式中：
ρ ——空气密度（kg/m3）；
A∞、Ad、Aw ——空气来流处、桨盘处、空气穿过桨盘下游处的桨盘面积（m2）；
U∞、Ud、Uw——空气来流处、桨盘处、空气穿过桨盘下游处的空气速度（m/s）。
单位时间内，桨盘上游处的空气动量为ρA∞U∞U∞。桨盘下游处的空气动量为ρAwUwUw；因此，空气的动量变化可以表示为：
$$ \rho {A}_{\infty} U_\infty - \rho {{{A}_{\mathrm{w}}}}U_{\mathrm{w}} = \rho A_{\mathrm{d}}U_{\mathrm{d}}{{(}}U_\infty - U_{\mathrm{w}}{{)}} $$ (2) 空气动量的变化是因为桨盘提供的压力所导致的，则由动量定理有：
$$ \rho A_{\mathrm{d}}U_{\mathrm{d}}{\text{(}}U_\infty - U_{\mathrm{w}}{\text{)}} = {\text{(}}\mathop p\nolimits_{\mathrm{d}}^ + - \mathop p\nolimits_{\mathrm{d}}^ - {\text{)}}A_{\mathrm{d}} $$ (3) 式中：
pd+、pd− ——桨盘上游、下游的压力（Pa）。
假定流经桨盘的气流满足伯努利方程，则对于桨盘上游有：
$$ \dfrac{{\text{1}}}{{\text{2}}}\rho \mathop U\nolimits_\infty ^2 + p_\infty + \rho {\mathrm{g}}h_\infty = \dfrac{{\text{1}}}{{\text{2}}}\rho \mathop U\nolimits_{\mathrm{d}}^2 + \mathop p\nolimits_{\mathrm{d}}^+ + \rho {\mathrm{g}}h_{\mathrm{d}} $$ (4) 对于桨盘下游有：
$$ \dfrac{{\text{1}}}{{\text{2}}}\rho \mathop U\nolimits_{\mathrm{w}}^2 + p_\infty + \rho {\mathrm{g}}h_{\mathrm{w}} = \dfrac{{\text{1}}}{{\text{2}}}\rho \mathop U\nolimits_{\mathrm{d}}^2 + \mathop p\nolimits_{\mathrm{d}}^ - + \rho {\mathrm{g}}h_{\mathrm{d}} $$ (5) 假设空气的流动是水平的(h∞=hd=hw），联立式（4）、式（5）得：
$$ \dfrac{{\text{1}}}{{\text{2}}}\rho {\text{(}}\mathop U\nolimits_\infty ^2 - \mathop U\nolimits_{\mathrm{w}} ^2 {\text{)}} = \mathop p\nolimits_{\mathrm{d}}^ + - \mathop p\nolimits_{\mathrm{d}}^ - $$ (6) 将式（6）代入式（3）中化简得：
$$ U_{\mathrm{d}} = \dfrac{1}{2}{\text{(}}U_\infty + U_{\mathrm{w}}{\text{)}} $$ (7) 即：
$$ U_\infty - U_{\mathrm{d}} = U_{\mathrm{d}} - U_{\mathrm{w}} $$ (8) 由式（8）可以看出，空气速度损失的一半发生在桨盘上游的区域内，而另一半则发生在桨盘下游的区域内。
令桨盘上游的速度损失为αU∞，即U∞−Ud=αU∞。则可定义桨盘的轴诱导因子α为：
$$ \alpha = {\text{1}} - \dfrac{{U_{\mathrm{d}}}}{{U_\infty }} $$ (9) 则桨盘提供的阻力为：
$$ T=({{\displaystyle p}}_{{\mathrm{d}}}^+-{{\displaystyle p}}_{{\mathrm{d}}}^{\_})A_{\mathrm{d}}=\text{2}\rho {A}_{\mathrm{d}}{{\displaystyle U}}_{\infty }^{2}\alpha (1-\alpha ) $$ (10) 风机的理想输出功率为：
$$ P = TU_{\mathrm{d}} = {\text{2}}\rho {A}_{\mathrm{d}}\mathop U\nolimits_\infty ^3 \alpha {{\text{(1}} - \alpha {\text{)}}^2} $$ (11) 无量纲化后的推力系数为：
$$ C_{\mathrm{T}} = \dfrac{T}{{\dfrac{{\text{1}}}{{\text{2}}}\rho A_{\mathrm{d}}\mathop {U}\nolimits_\infty ^2 }} = {\text{4}}\alpha {\text{(1}} - \alpha {\text{)}} $$ (12) 无量纲化后的功率系数为：
$$ C_{\mathrm{p}} = \dfrac{P}{{\dfrac{{\text{1}}}{{\text{2}}}\rho A_{\mathrm{d}}\mathop U\nolimits_\infty ^3 }} = {\text{4}}\alpha {{\text{(1}} - \alpha {\text{)}}^2} $$ (13) 式中：
α ——风机轴向诱导因子；
T ——风机桨盘阻力（N）；
P ——风机理想输出功率（W）。
-
贝兹极限是风电领域研究中关于风能利用效率的一条基本理论，同时也是第一个关于风轮气动的完整理论。“贝兹理论”建立的前提是假设存在“理想风轮”且需满足以下条件：风轮为一圆盘，轴向力沿圆盘均匀分布且圆盘光滑无摩檫力；风轮叶片无限多；风轮周围的气流静压相等；气流不可压缩，流速随时间均匀变化，不存在尾迹漩涡。
结合式（13）可知，若求解最大风能利用系数Cp，需要进行极值求解，如式（14）所示。
$$ \begin{split}&\dfrac{{\mathrm{d}}C}{{\mathrm{d}}\alpha }=\text{4(1}-\alpha {\text{)}}^{2}+\text{2(1}-\alpha )\text{4}\alpha =\\& (\text{1}-\alpha )(\text{1}-\text{3}\alpha )=\text{0}\end{split} $$ (14) 可得到2个解分别为：α=1时，Uw=−U∞，无意义；α=1/3时，风能利用系数最大，转化率最高为Cpmax，即贝兹极限。
$$ C_{{\mathrm{p}}{\mathrm{max}}} = \dfrac{{{\text{16}}}}{{{\text{27}}}} \approx {\text{0}}{\text{.593}} $$ (15) 式(15)表明风力发电机在转换能量的过程中是存在极限的，它指出在转换风能时，并非所有能量都能被有效利用，部分功率损失以尾流中旋转动能的形式存在。在实际应用中，风力发电机和发电形式的变化，使得能量的损失形式会改变，因此实际风能利用系数Cp<0.593。在叶片设计中，Cp的取值范围为0.25～0.45。
-
文章使用Fast.Farm开源软件对三风机在湍流风场中进行仿真计算，通过对单台风机和整个风电机组输出功率进行分析，从而优化风场布局。由于所用流场较为复杂，且计算时间过长，所以在进行大量工况前，对于流场的验证以及风场中多风机的气动特性进行验证是十分有必要的。
-
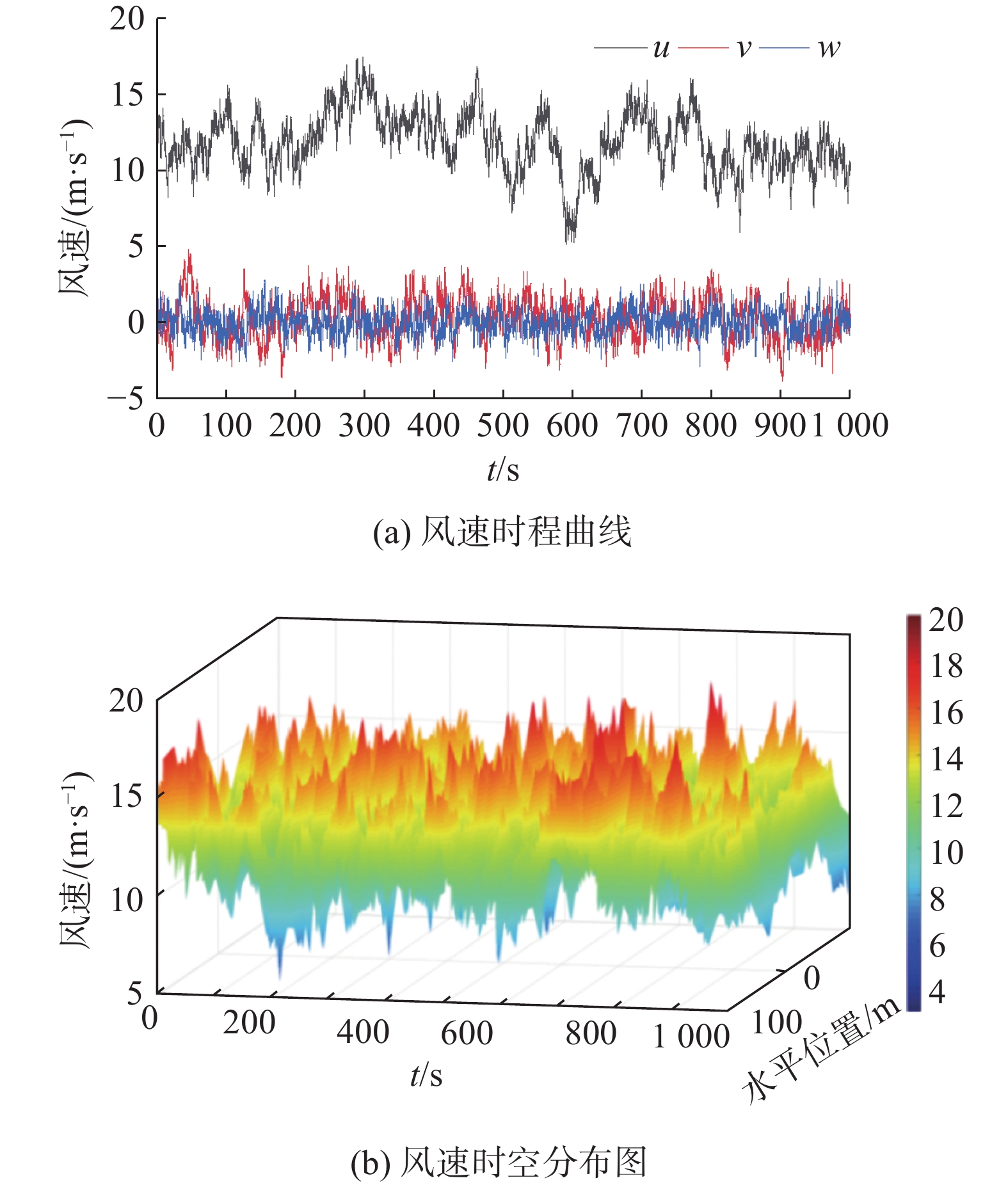
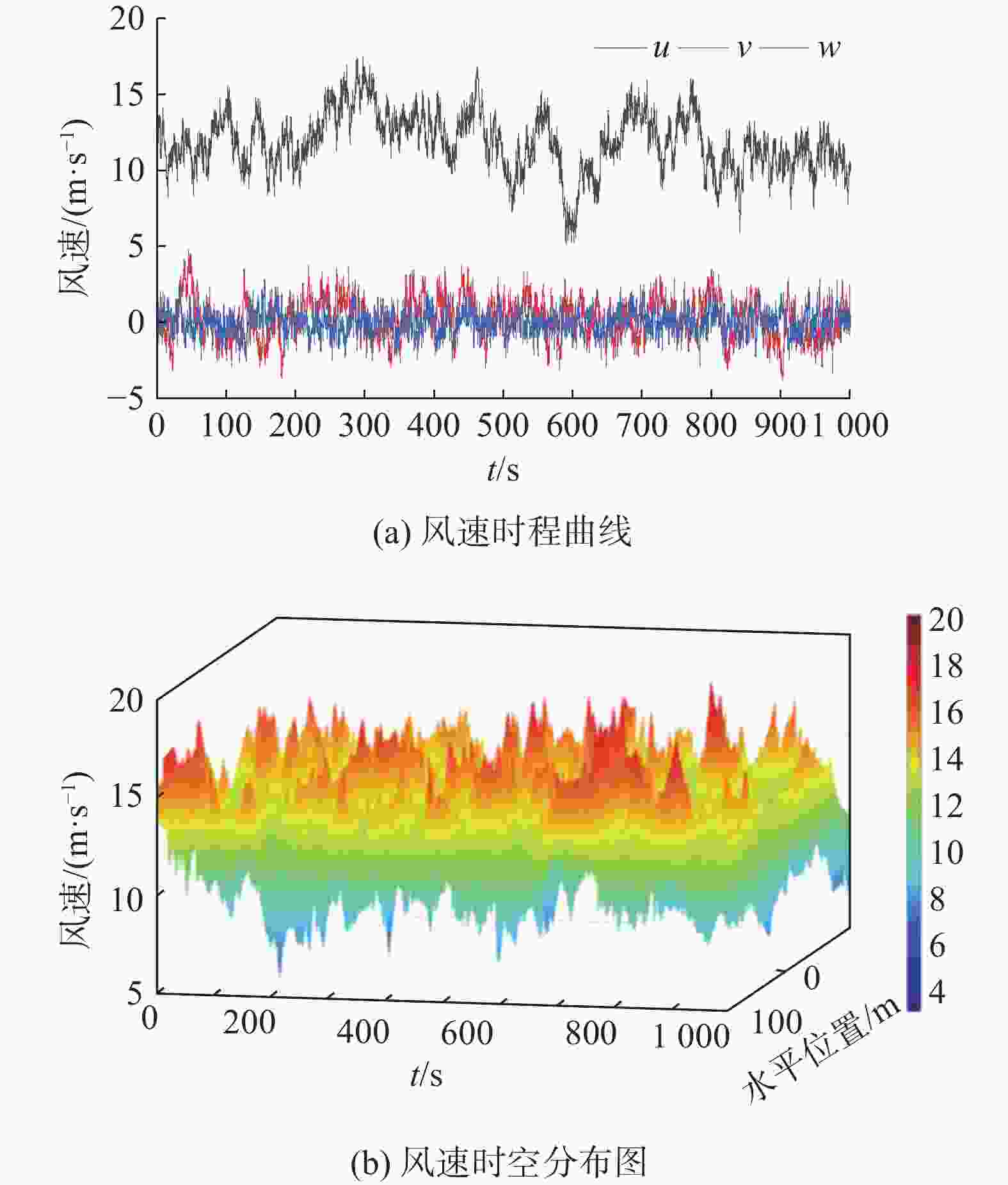
基于TurbSim软件，生成一个网格高度为175 m，宽度为
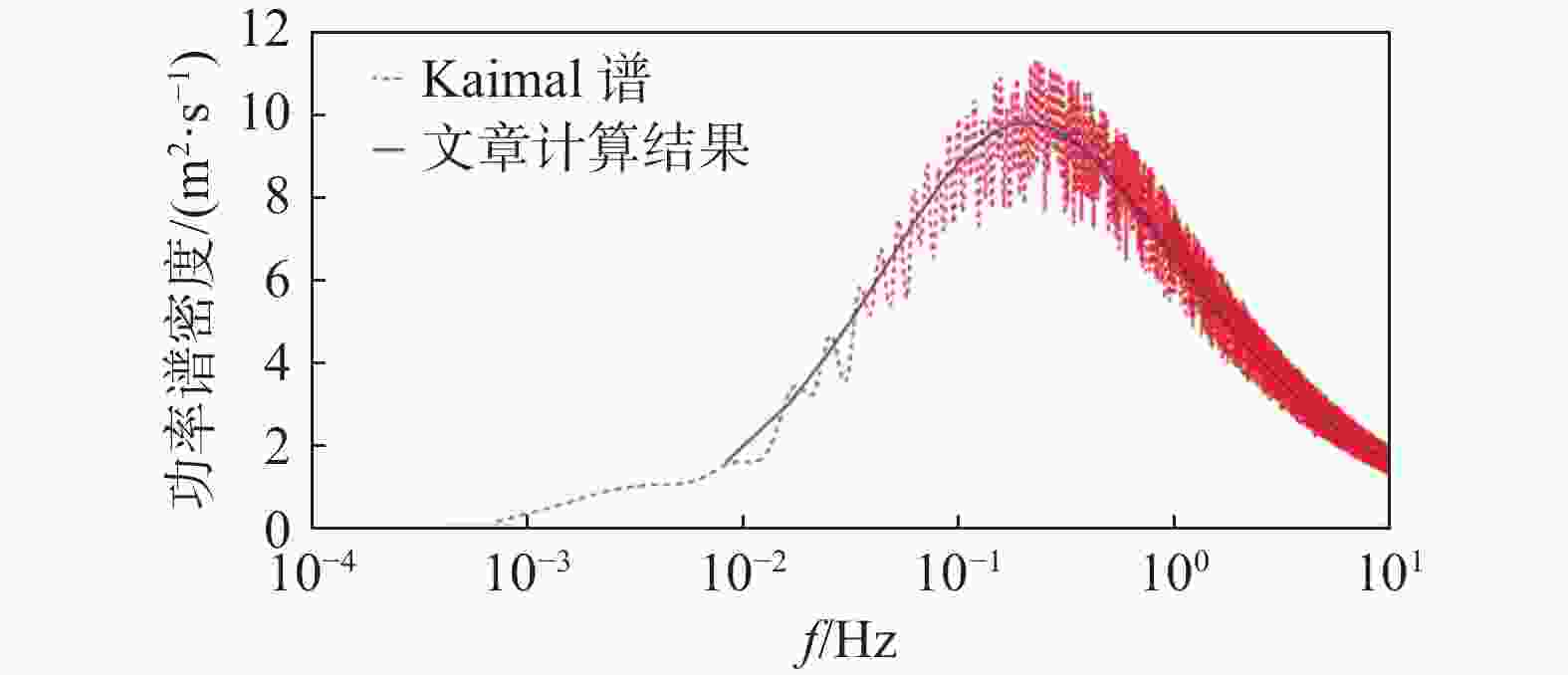
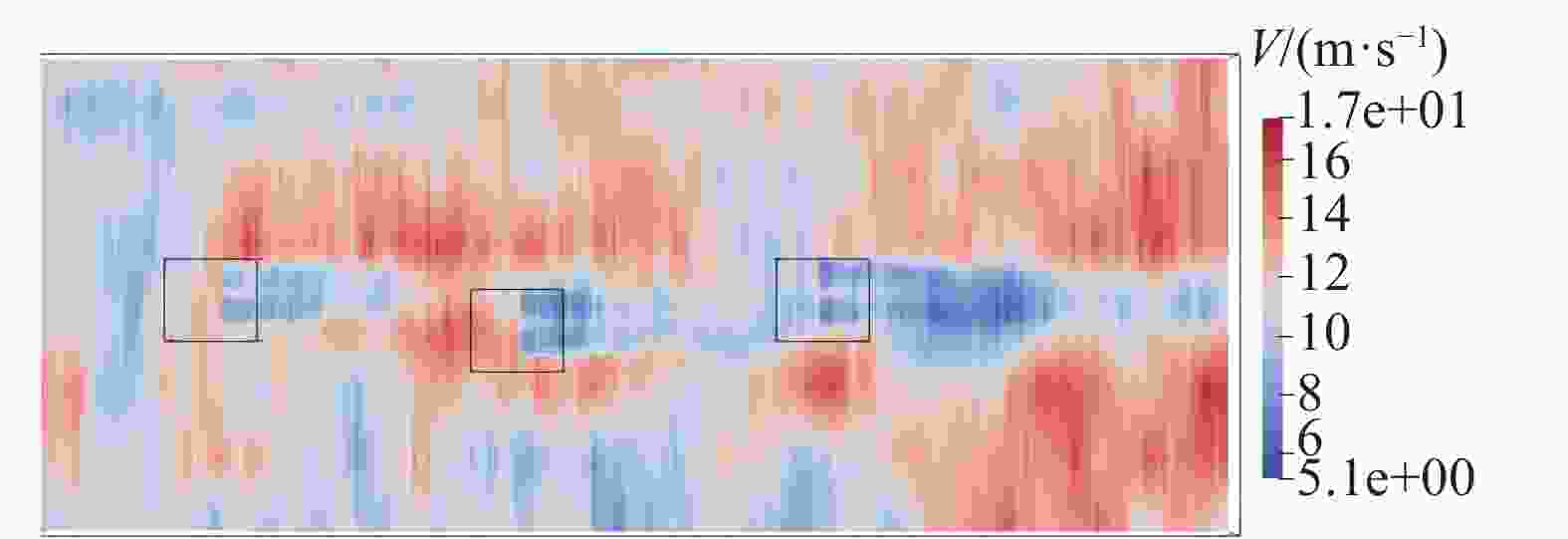
2.1 km，湍流强度为15%的湍流风，预测得到90 m高度处风速分布，如图1所示。
图 1 90 m高度处速度分布图
Figure 1. Speed distribution at an altitude of 90 m
模拟湍流风场时，Kaimal湍流风谱模型较为常用，且Kaimal风速谱可以用于对比预测风速和实际测量风速之间的频率分布情况，通过比较2个风速谱的相似程度，可以评估预测风速的准确性以及改进预测模型的必要性。
Kaimal湍流风谱某一方向上功率谱密度函数表达式为：
$$ {S_K}(f) = \dfrac{{4\sigma _K^2{L_K}/{{ u}_{{\mathrm{hub}}}}}}{{{{(1 + 6f{L_K}/{{ u}_{{\mathrm{hub}}}})}^{5/3}}}} $$ (16) 式中：
SK(f)——湍流速度分量K的功率谱密度（m2/s）；
f ——频率（Hz）；
σK ——风速分量K的标准差；
LK ——湍流速度分量K的积分尺度参数；
uhub ——轮毂高度风速（m/s）。
由图2可以看出，由风速时程曲线得到风速谱与Kaimal风速谱在大部分频率上都具有相似的能量分布情况，可以验证TurbSim软件生成的风速时程能满足Kaimal风速谱的要求。
图 2 文章计算结果与Kaimal谱对比图
Figure 2. Comparison between the simulated wind speed spectrum and the Kaimal spectrum
-
本节中计算了在高分辨率计算域和低分辨率计算域下不同网格大小Mesh1、Mesh2、Mesh3 3套网格模型的风机功率。在稳态风11.4 m/s（额定风速）风速下对5 MW风机进行数值模拟，得到的风机输出功率，如表1所示。其中功率对比率为计算结果与风机额定功率的比值，风机的额定功率（转子额定功率为5.29 MW）。Mesh1得到的计算结果为转子功率为5.28 MW；Mesh2得到的计算结果为功率为5.23 MW，比Mesh1小，误差在0.9%；使Mesh3得到的计算结果为功率为5.22 MW，与Mesh1相比相差1.1%。考虑到计算结果的精确度，文章后续的研究工作中，将使用网格分辨率为Mesh1的网格模型作为计算参数。
表 1 不同网格尺寸下单风机功率对比
Table 1. Comparison of the power of the single wind turbine at the different grid sizes
工况 低分辨率计算域
网格大小/m高分辨率计算域
网格大小/m风机功率/
MW功率
对比率/%Mesh1 10 5 5.28 99.81 Mesh2 10 10 5.23 98.87 Mesh3 20 10 5.22 98.68 -
Fast.Farm是一款非线性时域多物理场工程仿真工具，由多个子模块组成，每个子模块代表风电场中一个不同的物理场，可以用来计算风电场内机组发电量和结构载荷的中保真度多物理工程工具[21]。Fast.Farm软件的优势主要在于其能以较低的计算成本进行多次迭代计算和对可能存在的情况进行模拟[22]。文章模拟计算Horns Rev风电场，将计算结果与文献[23]中实测数据进行对比，以Pi表示各列风机的输出功率，P1表示迎风向第一列风机的输出功率，Pi/P1为无量纲输出功率。由图3可知，各列风机无量纲输出功率与实测数据的误差较小，均在可允许范围内，验证了文中方法可以较好的模拟风电场情况。
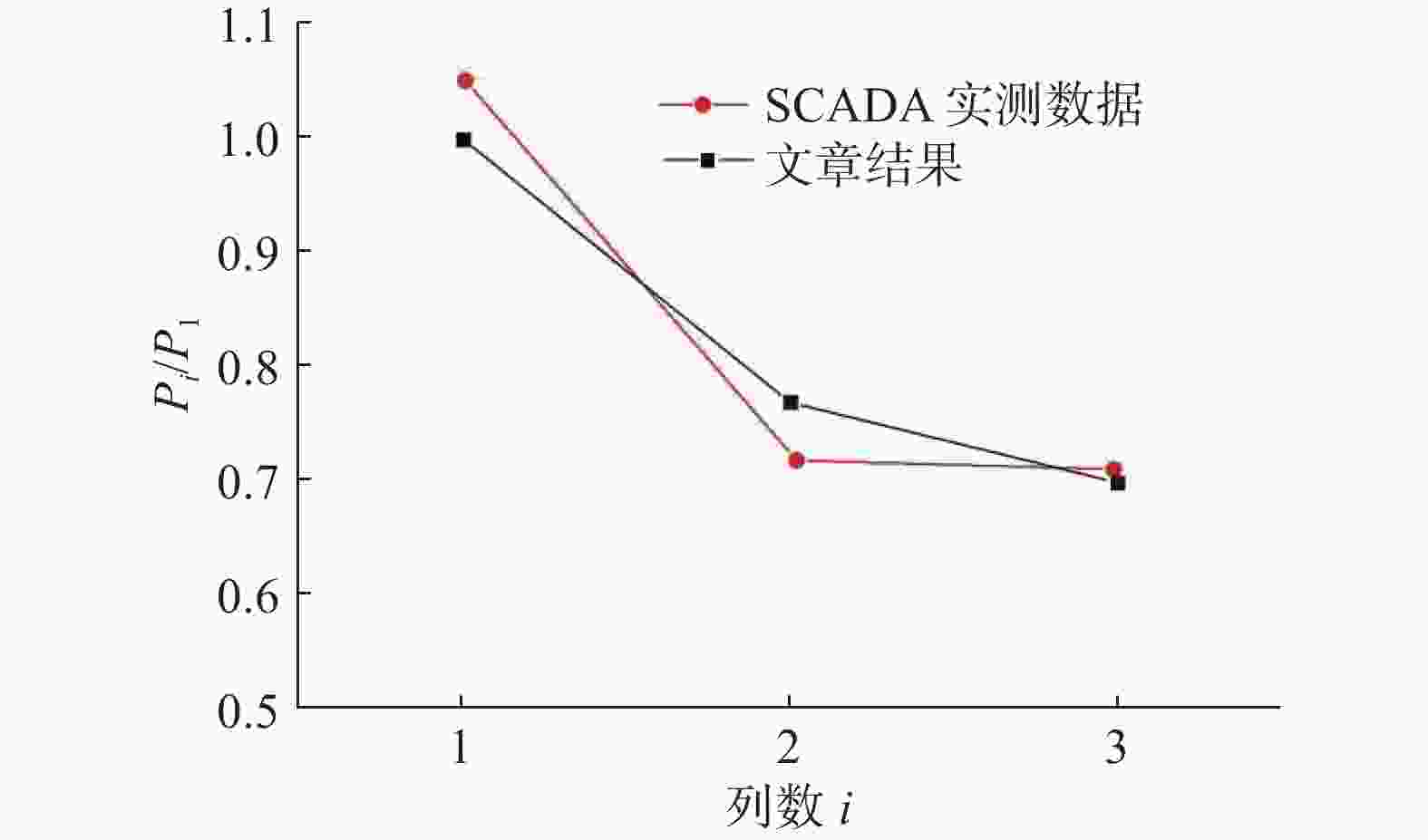
图 3 文章计算结果与SCADA实测数据对比情况
Figure 3. Comparison between the calculated results in this paper and the measured data of SCADA
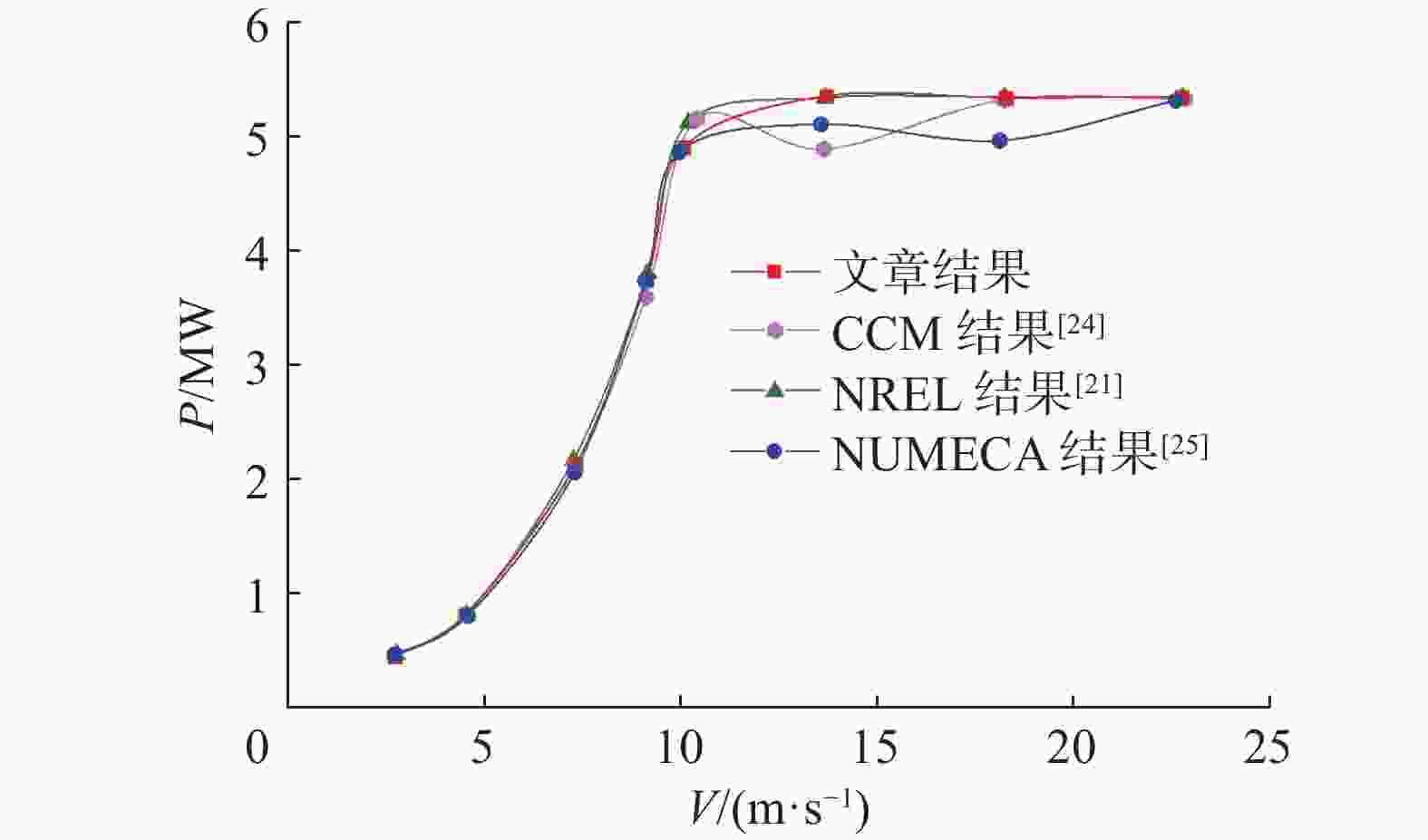
采用NREL 5 MW风机模型进行数值模拟计算，得到风速在3～25 m/s之间稳态风的功率，并与相关文献进行对比。由图4可知，模型计算得出的功率数据与NREL设计数据基本一致，除风速为3 m/s工况，其余工况误差在3%以内；风速在低于10 m/s时，结果与各实验对比数据基本吻合，风速在高于10 m/s时误差也处于能接受的范围内。
图 4 单风机功率对比图
Figure 4. Comparison of the power of a single wind turbine
-
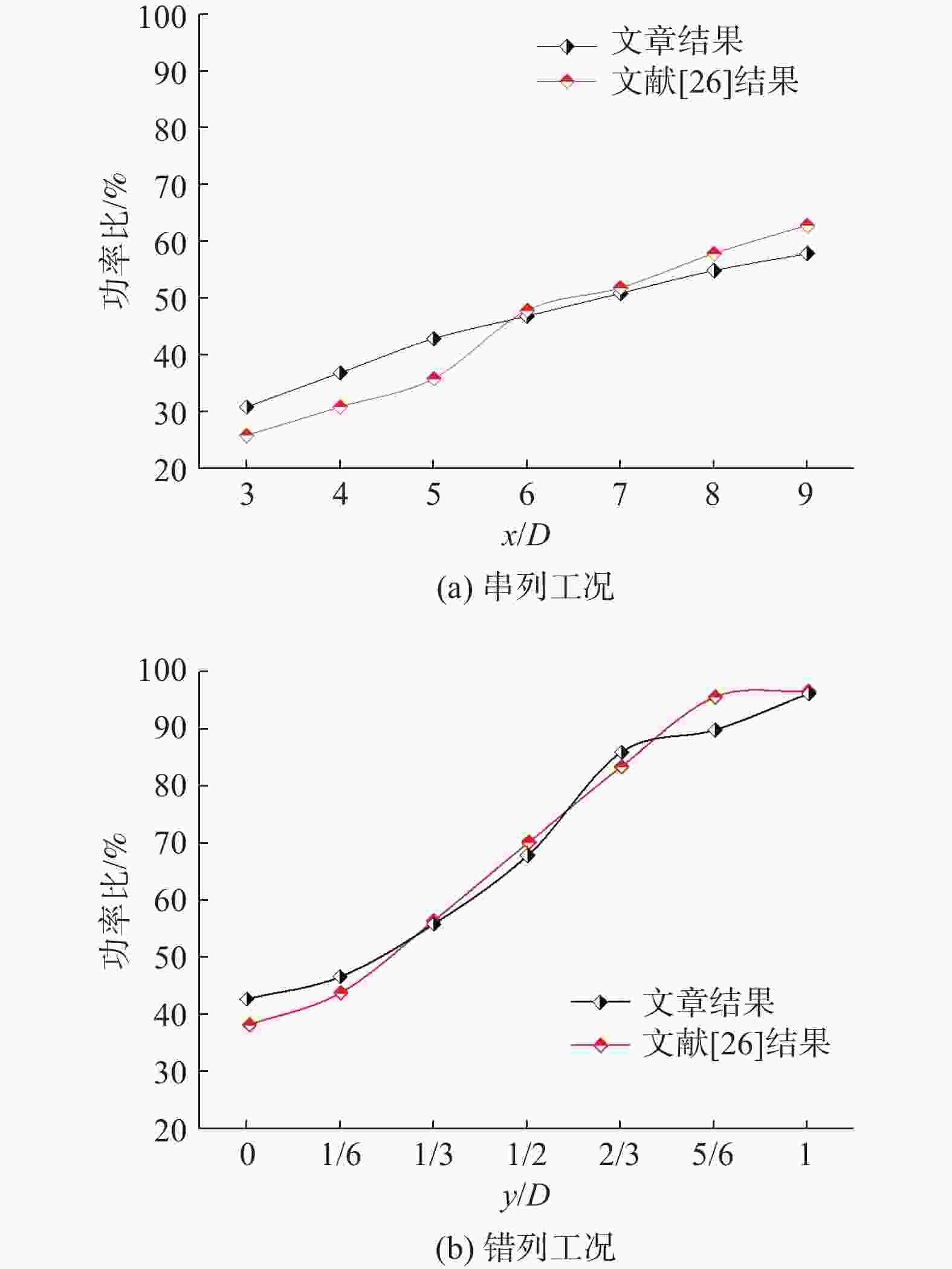
文章对串列及错列2种不同排布方式的三风机功率进行研究，进一步与文献[26]双风机结果进行对比验证。通过图5（a）（图中功率比为上下游风机输出功率之比，x为风机间平行风向距离，y为风机垂直风向距离）可以发现，串列工况下文章结果与文献[27]结果虽有所偏差，但大致变化趋势相同，最大误差为7.13%，在允许范围内。误差是由于所用风机尾流解析模型及风机功率求解理论有所差别而产生的。错列条件下文章结果曲线与文献结果曲线较为贴合，如图5（b）所示，风机错列使得下游风机受上游风机的尾流影响减弱，因此风机尾流解析模型所造成的误差会减小。进一步验证了文章选取的计算模型及其参数设置可有效解决多风机输出功率问题。
-
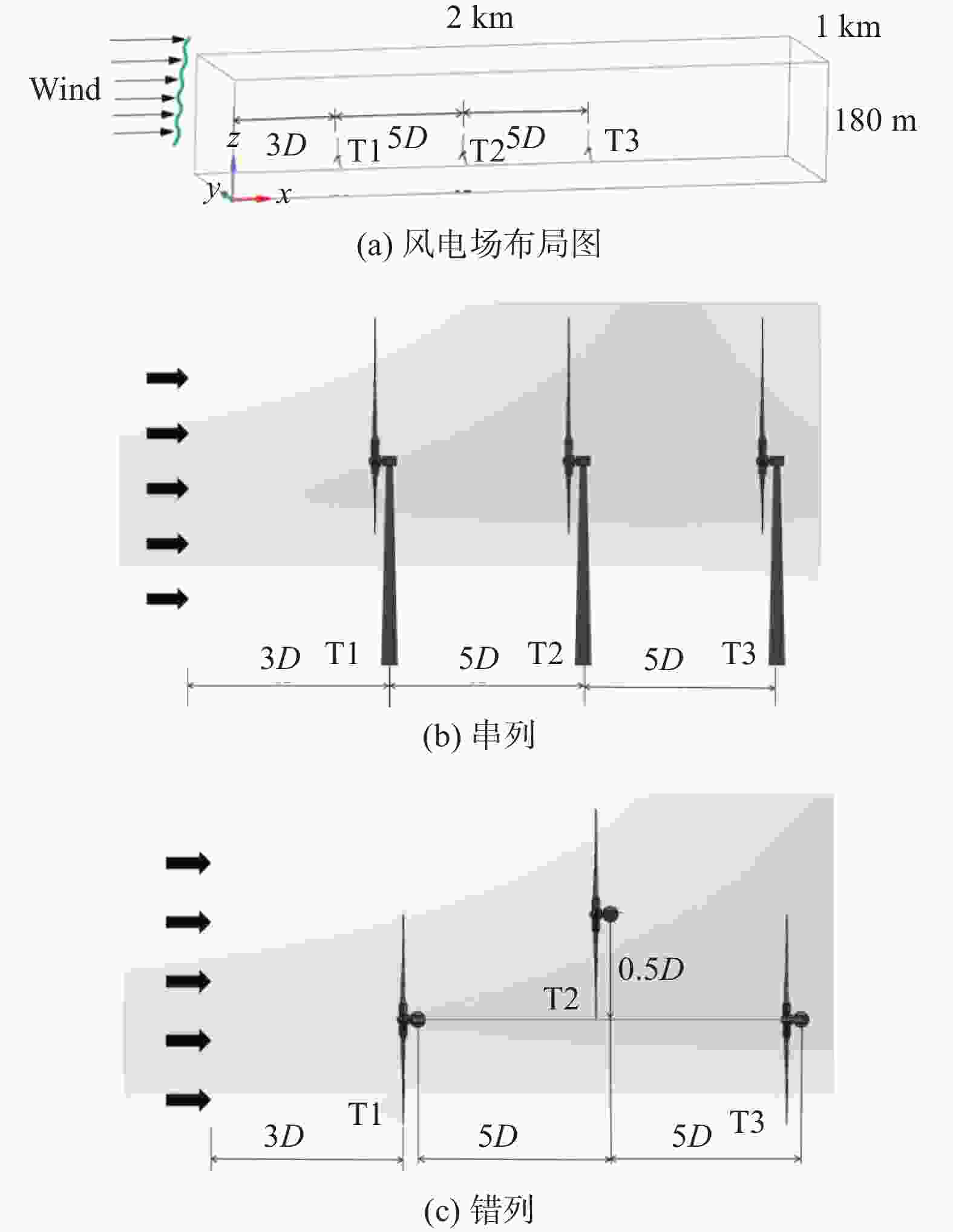
图6为纵向间距为5D（D为风机直径，取126 m）三风机串列及错列情况下风场模型示意图。上游风机（T1），中游风机（T2），下游风机（T3）串联时，T1、T2、T3风机均位于y=0坐标轴上，见图6（b）。错列时T2风机沿y轴正方向偏移，图6（c）为T2风机错列距离为0.5D工况示意图。为使入流发展充分，T1风机与湍流风入口纵向距离为3D。湍流风的方向均为沿x轴正方向，风轮平面垂直于湍流风的来流方向。为使风场在计算域内发展充分，每次仿真的时长为
8000 s，然而由于初始阶段流场的不稳定性以及风机机组未达到稳定状态，为确保计算结果的准确性，仅考虑将仿真过程后期阶段（6000 ～8000 s）的平均值作为最终的计算结果。这样的参数设置不仅有助于提高计算效率，还能够保证数值模拟结果的可信度，从而为风机性能的准确评估提供了可靠的基础。
图 6 纵向间距L=5D三风机群计算模型示意图
Figure 6. Schematic diagram of the calculation model of the longitudinal spacing L=5D three-wind turbines
-
为了研究在不同间距下对于风电场功率的影响大小，选取风场湍流度为15％，轮毂高度处的速度为11.4 m/s。算例1中将风机纵向间距设为2D～11D；考虑到风电场中风机排布一般较为密集，为使风电场风资源得到合理利用，一般风机间距不超过5D，但过小的间距会使风机间尾流影响较大，故算例2将风机纵向间距设为5D，第二台风机与首台风机的错列距离在0～1D范围内；具体设置如表2所示。
表 2 算例参数设置统计表
Table 2. Example parameter setting statistical table
算例编号 排布方式 纵向间距 第二台风机错列距离 1 串列布置 2D～11D 0 2 错列布置 2D～11D 0～1D -
在湍流风环境下多风机的发电效率优化研究中，风机的纵向间距是一个至关重要的参数，直接影响着风机的协同运行和发电性能。本节通过分析串列三风机间纵向间距在2D～11D之间变化时，后排风机输出功率及总功率变化情况，再进一步分析风机纵向间距对风电场总功率及总功率提升率的影响。
由于其他风机对T1风机的影响很小，所以在所有工况下T1风机的功率都保持不变，为4.48 MW。图7为不同纵向间距下后排风机的输出功率图，其中包括所选仿真时段内出现的最大输出功率、最小输出功率以及平均功率，随着风机间纵向间距的增加，后2台风机的发电量均会逐渐增加。风机间距在2D～5D内变化时，T2和T3风机的功率增长率均会增加，导致风电场的发电效率提升较大；而当风机间距由5D增加到8D时，T2和T3风机的功率增长率呈下降趋势，此时风电场功率提升量相对缓和；当风机间距超过8D后，T2和T3风机的功率增长率又开始持续增长，风电场总功率提升加快。当纵向间距为2D时，处于下游的风机与上游风机的输出功率相差较大，此时T2与T3风机之间的输出功率相差0.72 MW；纵向间距大于10D时，T2与T3风机输出功率仅相差0.04 MW。文献[27]中也报道了类似结果，下游风机要达到与上游风机相同的输出功率，需要与上游风机保持较大的距离。
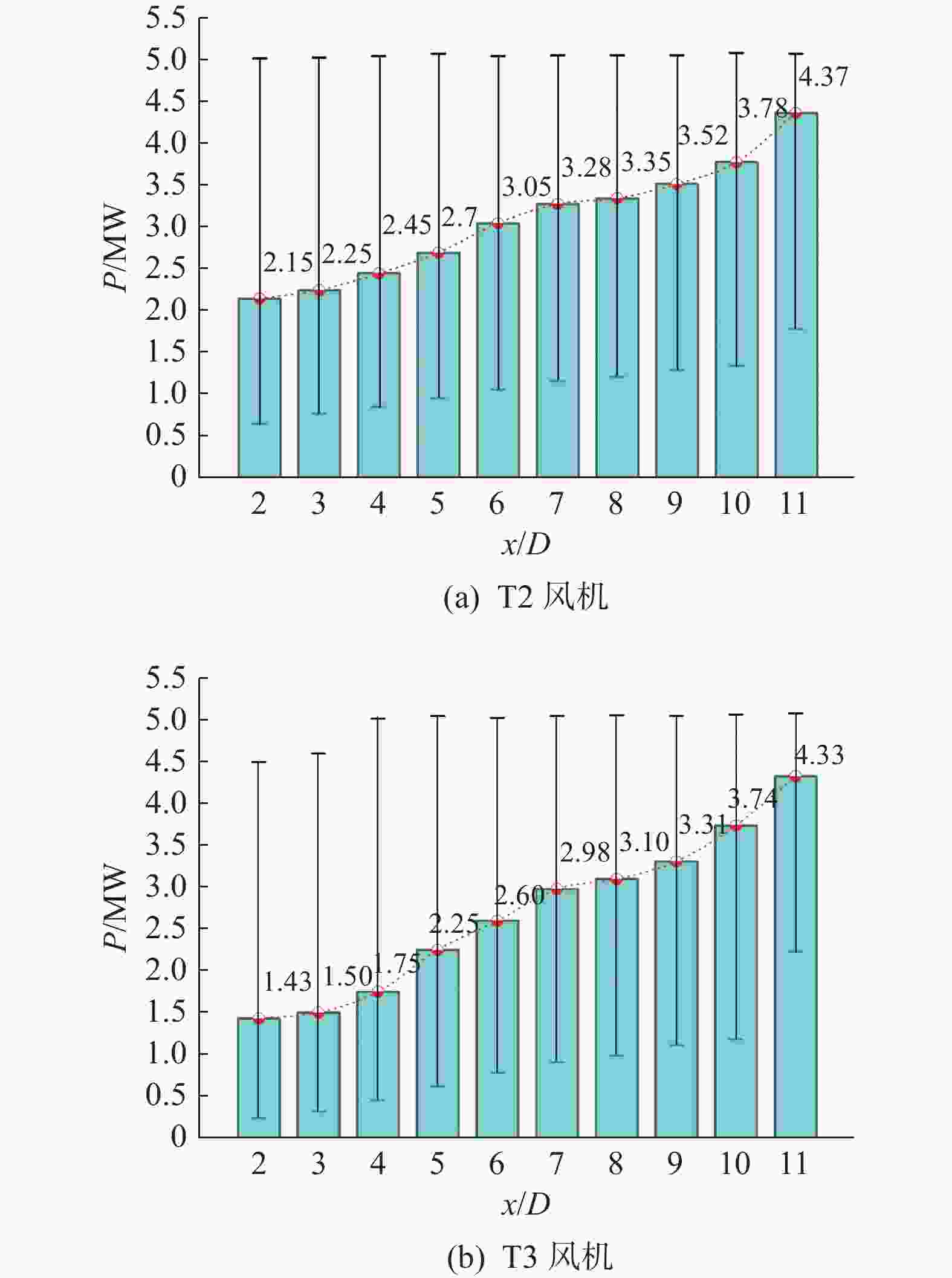
图 7 不同纵向间距下后排风机输出功率
Figure 7. Output power of rear exhaust wind turbines under different longitudinal spacings
当风机纵向间距较小时，后排风机的功率均偏低，此时后排风机完全处于前排风机尾流区域内，导致前排风机尾流到达后排风机时，尾流速度损失恢复较弱，受上游风机尾流影响较大；随着纵向间距的增加，尾流速度损失逐渐得到恢复，后排风机输出功率也会增加。由图8可以发现当风机纵向间距由4D增大到5D时，风电场的总功率出现第一次大提升，提升率为8.64%；从图5可以发现，此时风电场总功率发生较大提升主要来自于T3风机输出功率的大幅提升，T2风机的提升较为稳定，这是因为T3风机受T1和T2风机尾流的共同作用。如图9所示，风机纵向间距为5D时相比于3D时，T1风机的尾流在到达T3风机时尾流损失已有了较好的恢复，此时T1风机尾流对于T3风机的影响减弱，使得其提升率较T2风机增加更为明显。另外，当风机纵向间距由10D增大到11D时，风电场的总功率会出现第二次大提升，提升率为9.83%，此时T2和T3风机的功率都有显著增加，该工况下风速经过较长距离的恢复，到达T2风机时的风速与经过T1风机的风速相差不大，所以下游风机受到上游风机的影响较小。两次总功率大幅提升转折点都在风机间距由9D变为10D时。无论是相邻还是相隔风机，纵向间距达到10D时可以较大程度提升风电场的发电效率。
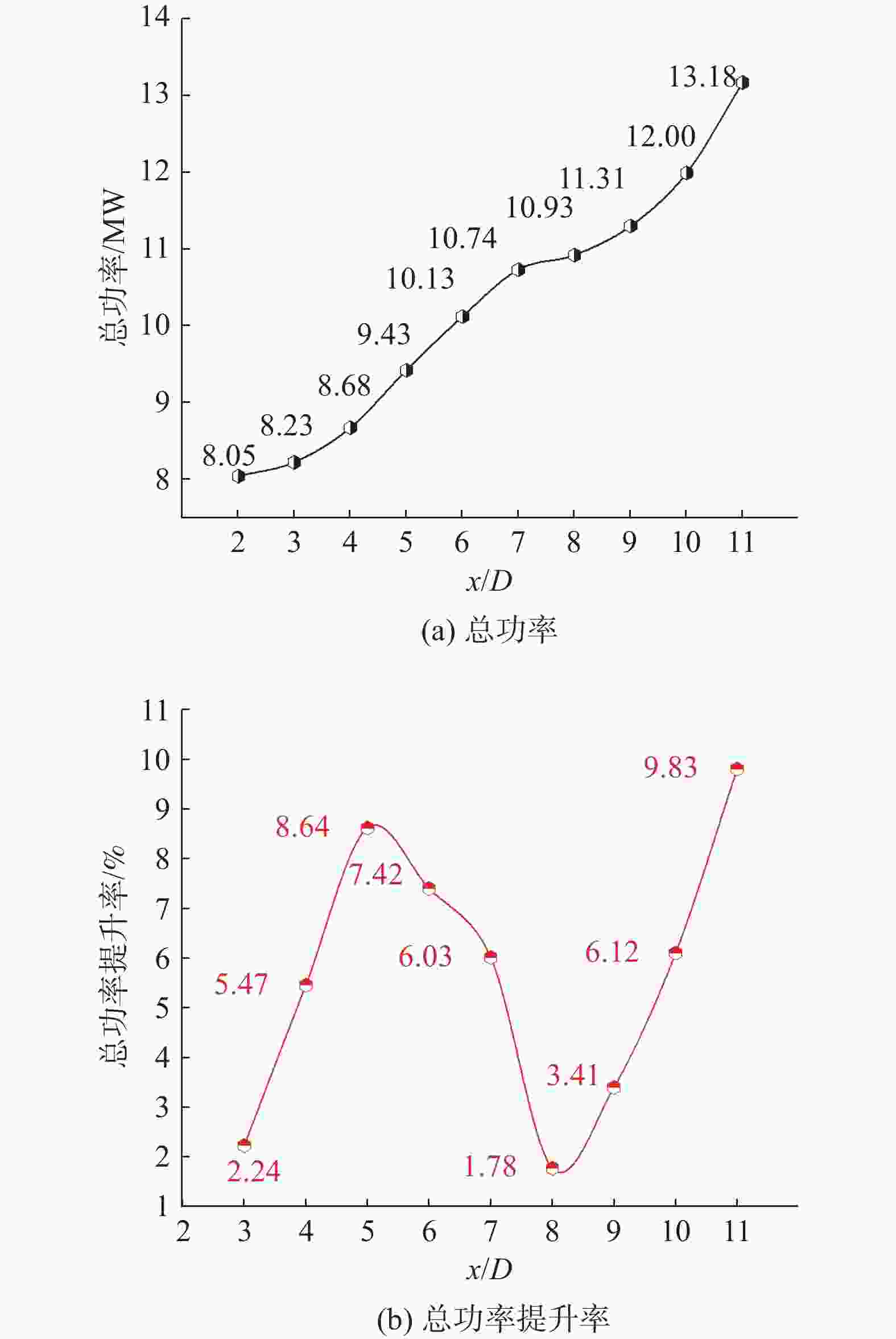
图 8 不同纵向间距下总功率及其提升率对比图
Figure 8. Comparison of total power and its improvement rate at different vertical spacings
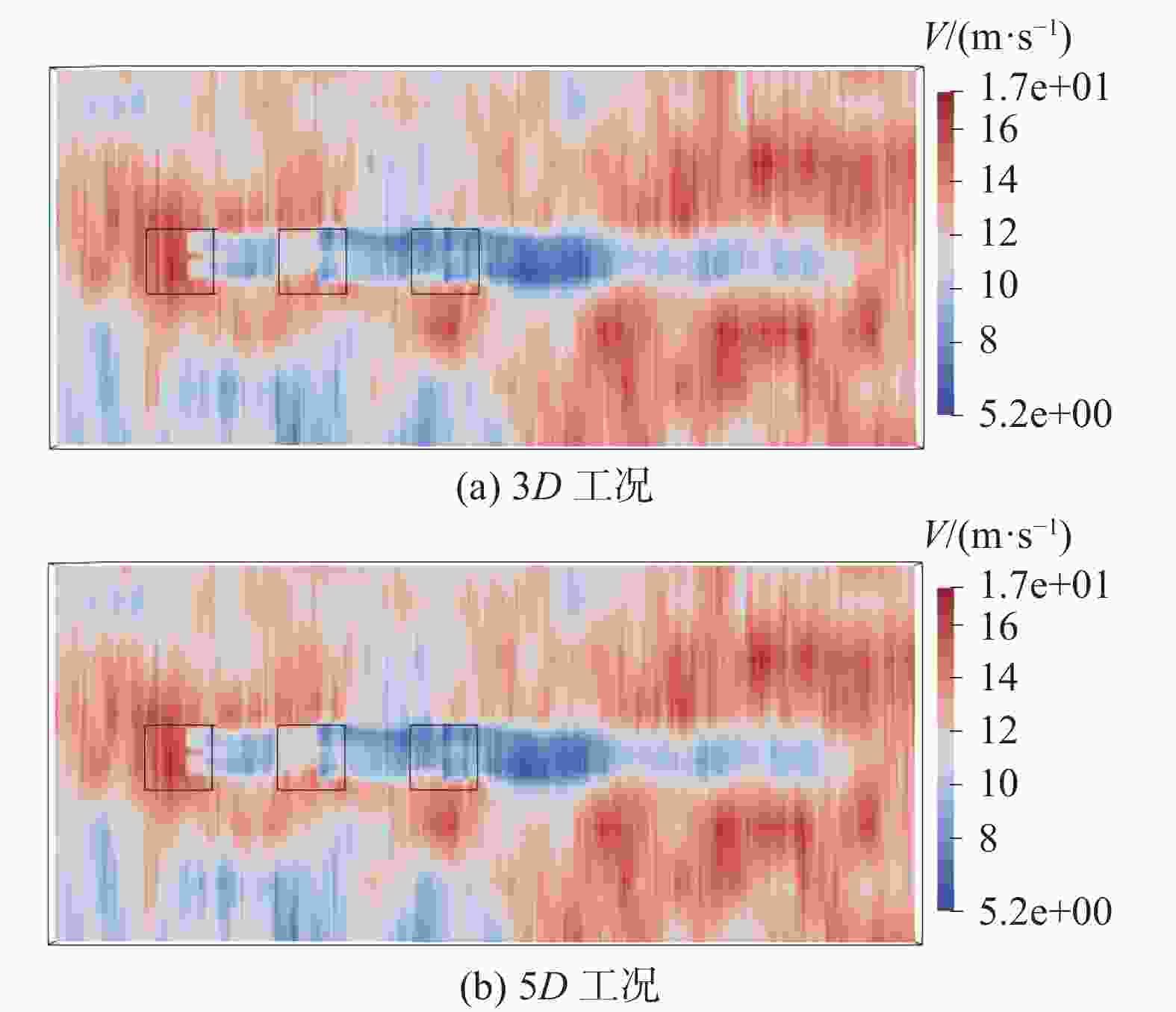
图 9 不同纵向间距风电场速度分布
Figure 9. Speed distribution map of wind farms with different longitudinal spacings
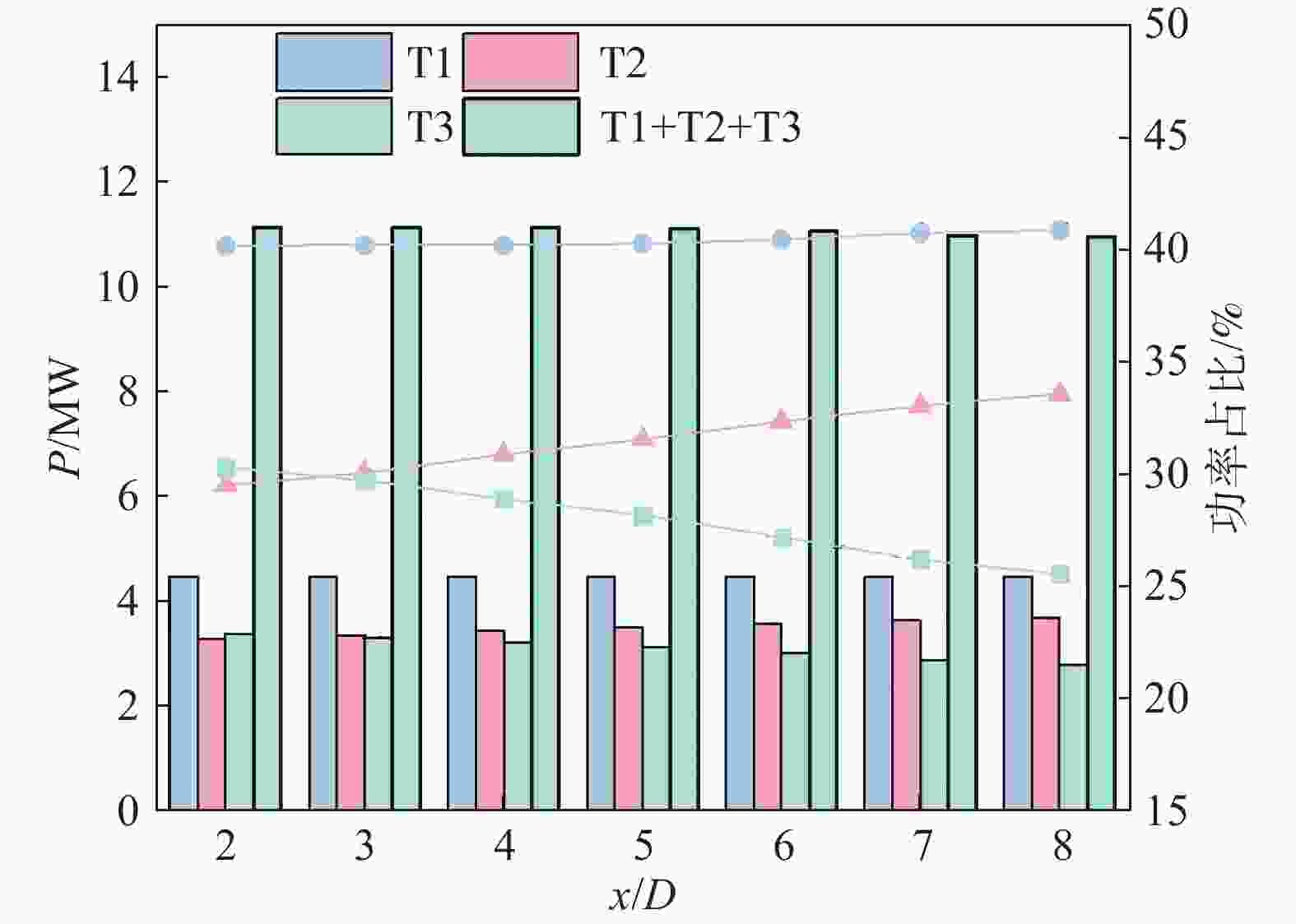
在串列条件下当T1与T3风机纵向距离固定为10D时，分析改变T2与T1风机的纵向距离对于后排风机功率的影响，同时获得T2风机在风场中的最优位置，从而得到该工况下风电场最大总输出功率。由T3受T1风机的尾流影响很小，导致风电场总输出功率变化的主要因素为T2风机尾流对T3风机的影响及T1风机尾流对T2风机的影响。由图10可以看出，当T1与T3风机纵向间距固定为10D，T1与T2风机相距5D时，T2与T3风机的输出功率占总输出功率的28.63%和23.86%，两者相差4.77%。
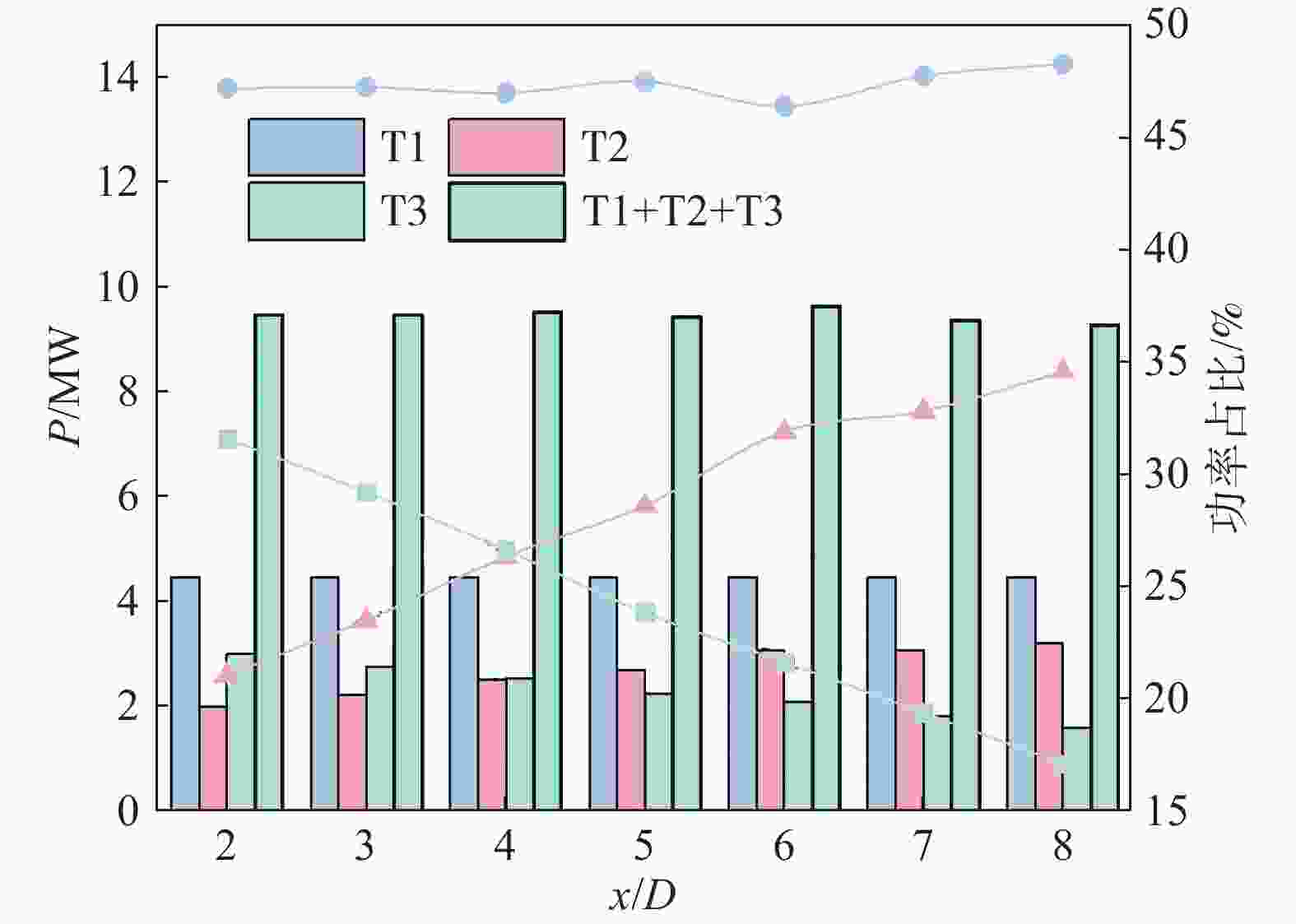
图 10 T2风机在不同纵向间距下风电场总功率变化情况
Figure 10. Change in the total power of wind farms under different longitudinal spacings of T2 wind turbine
以T2与T1风机相距5D时为对比，对T2风机在风场中位置变化对风电场总功率的影响情况进行分析。T2与T1风机纵向间距小于5D时，风电场功率均有不同程度的提升。其中，当T2与T1风机相距4D时风电场总功率达最大值，此时T2与T3风机的输出功率分别占总输出功率的26.34%和26.65%，相差仅0.31%。当T2风机向T1风机靠近时，T2风机将受到来自T1风机更大的尾流影响，与此同时随着T2与T3风机的距离增大，T2风机尾流速度恢复更快，T3风机的入流条件得到改善，功率会有所提升。在纵向间距小于5D时，T3风机的功率已大于T2风机的输出功率，且相对于纵向间距为5D时，T2风机输出功率的提升量大于T1风机因纵向距离减小而损失的输出功率。T2与T1风机纵向间距大于5D时，仅仅在T2与T1风机纵向间距为6D时，风电场总功率有提升，其余2种工况均未对总功率起到提升作用。纵向间距大于6D时，T2与T1风机距离变小，使得T2受T1风机尾流影响增大，输出功率也会降低，T2与T3风机距离增加，但与T1风机间距较小时会导致其自身输出功率大幅降低，T3风机的输出功率略有提升，但T2风机的输出功率下滑严重，导致风电场总功率有所降低。其中，当纵向间距为8D时，风电场总功率最小，而纵向间距为2D时，风电场总功率有一定提升，这表明串列条件下T2与T1风机距离不宜太近。综上，当T1与T3风机距离固定，T2与T1风机间距离小于T2与T3风机距离时，对于风电场总功率提升效果更佳，即通过牺牲前排风机的输出功率来提高后排风机的输出功率对于风电场输出功率的优化有一定效果，且在风场中各风机间距接近时，可使风电场输出功率处于较高水平，这表明在风电场布局中应尽量平均布置风机位置。
-
通过上一节分析可知，前排风机尾流对后排风机的尾流干扰严重，影响风电场整体输出功率。尾流抑制策略对于提高风电场整体发电量有明显作用，而改变前后排风机的横向间距也同样是最为基本的尾流抑制策略。本节研究了错列布置下三风机风电场的输出功率，分析了错列布置下风机间的尾流干扰，为风电场的选址提供一定的数值依据。图11为不同横向间距下后排风机最大、最小及平均输出功率，设定横向间距在0～1D之间，涵盖了从风轮重叠到风轮面相邻的范围，同时设定风机间纵向间距为5D，分析T2与T1风机的横向间距改变对后排风机功率以及风电场总功率的影响。当横向间距由0增加到1D时，T2风机输出功率由2.70 MW增长到4.19 MW，增加了55.18%，相对于额定功率，其功率损失率由46.00%降低至16.20%；T3风机输出功率也由2.25 MW增长到3.94 MW，增加了75.11%，相对于额定功率，其功率损失率由55.00%降低至21.20%。T2和T3风机的功率呈稳定增长，且其增长速率相近，这表明横向间距增加对T2和T3风机的输出功率影响大致相同。另外，T2和T3风机的最大功率均维持在额定功率附近，表明风机均可接收到使其达到额定功率的风能，而最低功率有所差异，随距离的增大而增大。当风机之间的横向间距增加时，T2和T3风机在风场中的位置更远，所有机组间的相互影响很小[28]，此时，T3风轮平面与T2风机尾流区域重叠部分减小，T3风机能够更有效地捕获风能，从而增加发电量。
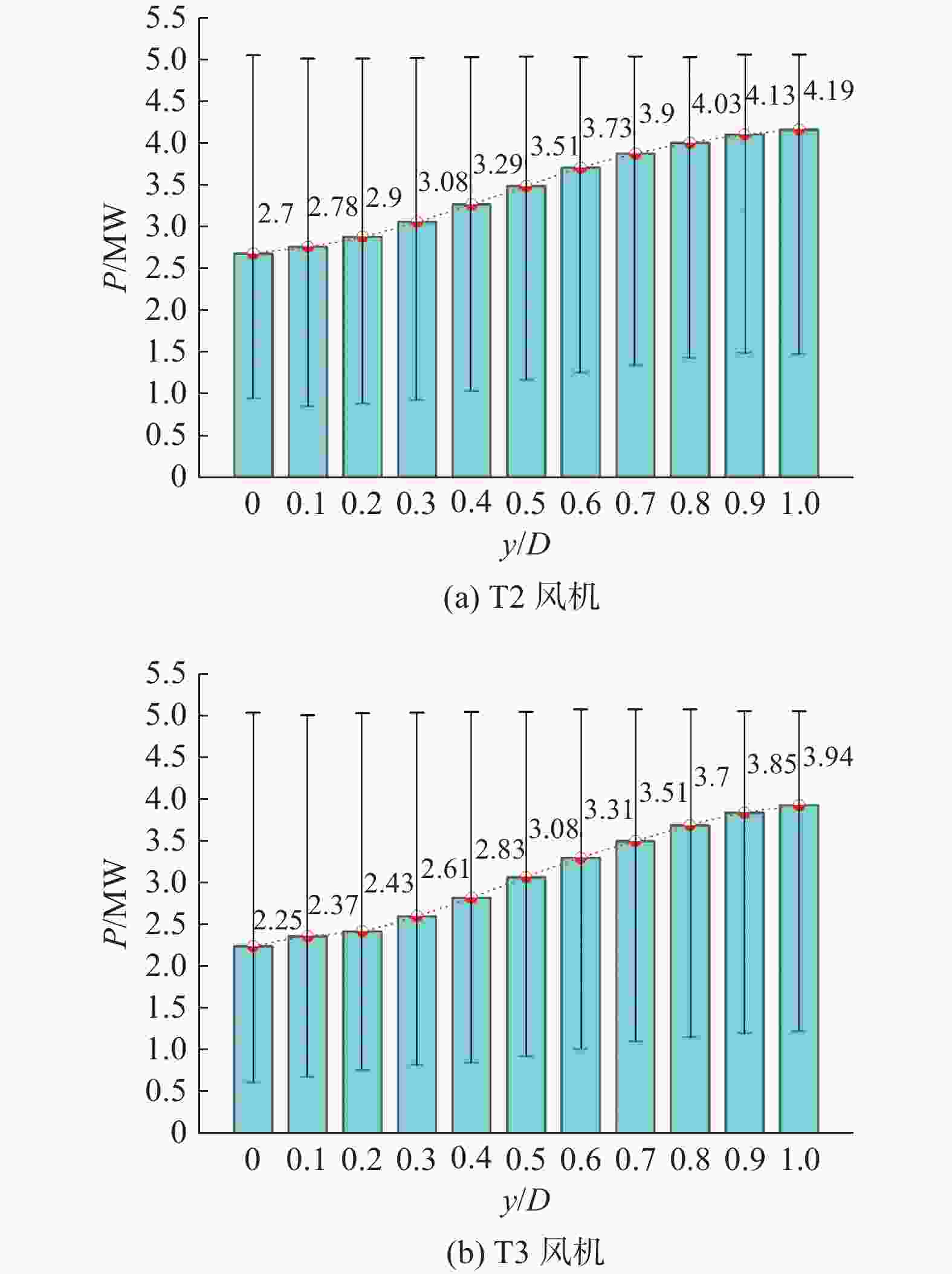
图 11 不同横向间距下后排风机输出功率
Figure 11. The output power of the rear wind turbine at different lateral spacings
图12为不同横向间距下总功率及其提升率对比图，当T2与T1风机横向间距由0增加到1D时，风电场总功率由9.47 MW提升到12.62 MW，提升了33.26%。风机之间的距离增大，减小了阵列效应的影响，相邻风机之间的阻尼效应减弱，风场流经过每个风机时不受到相邻风机的干扰，改善了风场中的空气流动。这使得风速分布更均匀，T2和T3风机更容易获得高速风，从而增加其发电量。随着横向间距的增大，总功率的提升率会存在一个最优区间，即当横向间距在0.4D～0.6D区间内，总功率提升率较大，在0.5D时达最大值4.43%。
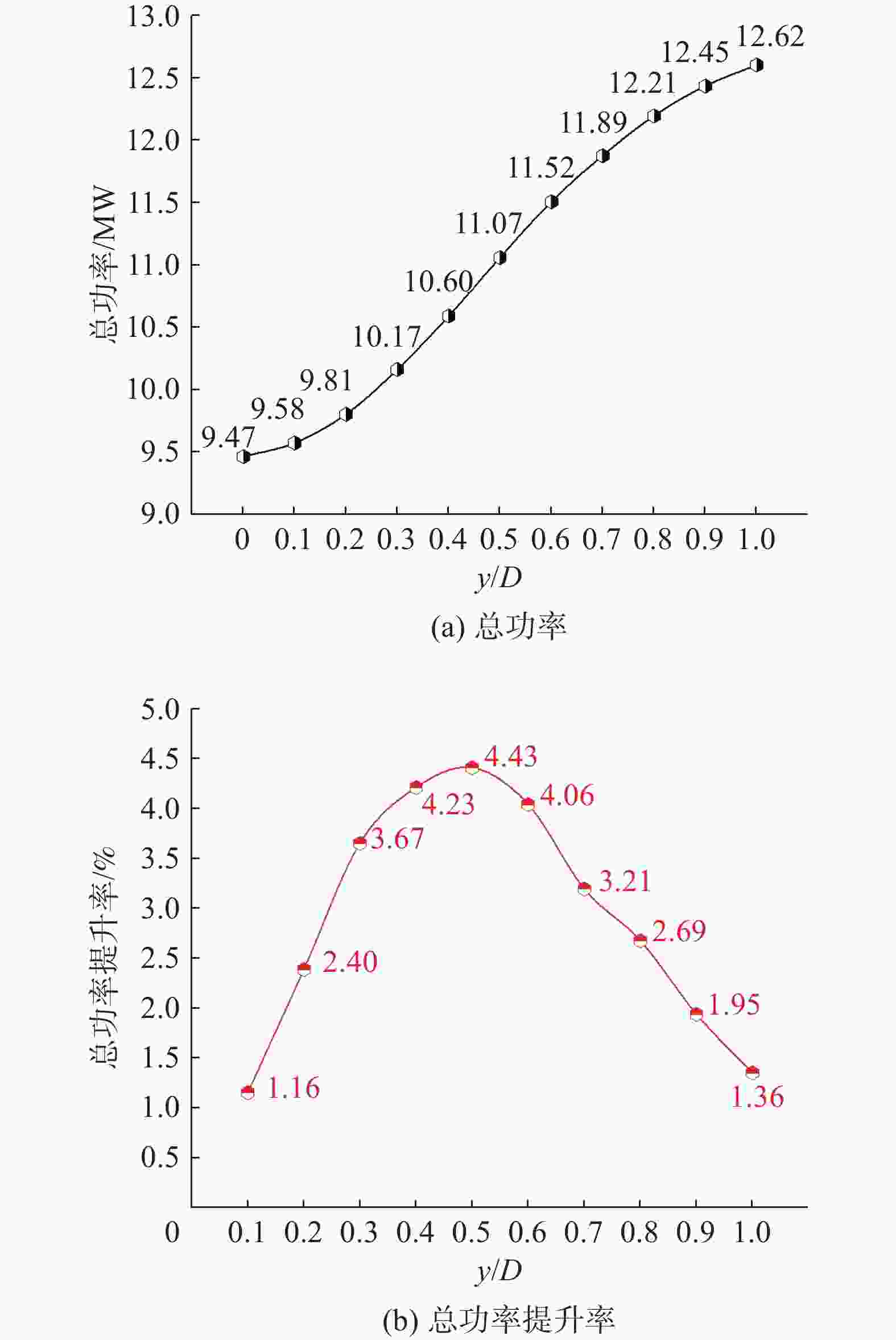
图 12 不同横向间距下总功率及其提升率对比图
Figure 12. Comparison of total power and its improvement rate under different lateral spacings
对于T2风机而言，由于自身的横向偏移，其受到T1风机的尾流效应有所减弱，功率也有所提升。对于T3风机而言，因为T2风机的错列使得其尾流发生偏转，来自T1风机的尾流损失也有一定的恢复，所以相对于串列情况下，其入流条件会有明显改善。图13为横向错列间距0.5D时的风电场速度图，相比于图9（b）可知，T2风机风轮有大部分面积未处于T1风机尾流区域内，T3风机只有少部分风轮区域受到T2风机尾流的遮挡。综合考虑风电场的利用率，横向错列距离在0.4D～0.6D时，风电场布局是最优的，这说明在这个范围内调整横向间距既能减小风机间尾流影响，又能充分利用风电场资源，从而实现风电场功率最优。
图 13 横向间距0.5D风电场速度分布图
Figure 13. Velocity distribution of wind farm at a horizontal spacing of 0.5D
确定了T2风机的最佳位置后，即当T2风机与T1风机纵向距离为4D时，再对其进行横向间距进行研究。如图14所示，位置优化前后风电场总功率及其提升率的上升趋势基本一致。在总功率方面，T2风机位置优化后总功率均大于优化前，进一步验证了对于T2风机位置的优化是可行的。分析2种工况下总功率提升率可发现其变化趋势大致相同，且同样在横向间距为0.4D～0.6D时，总功率的提升较为明显。
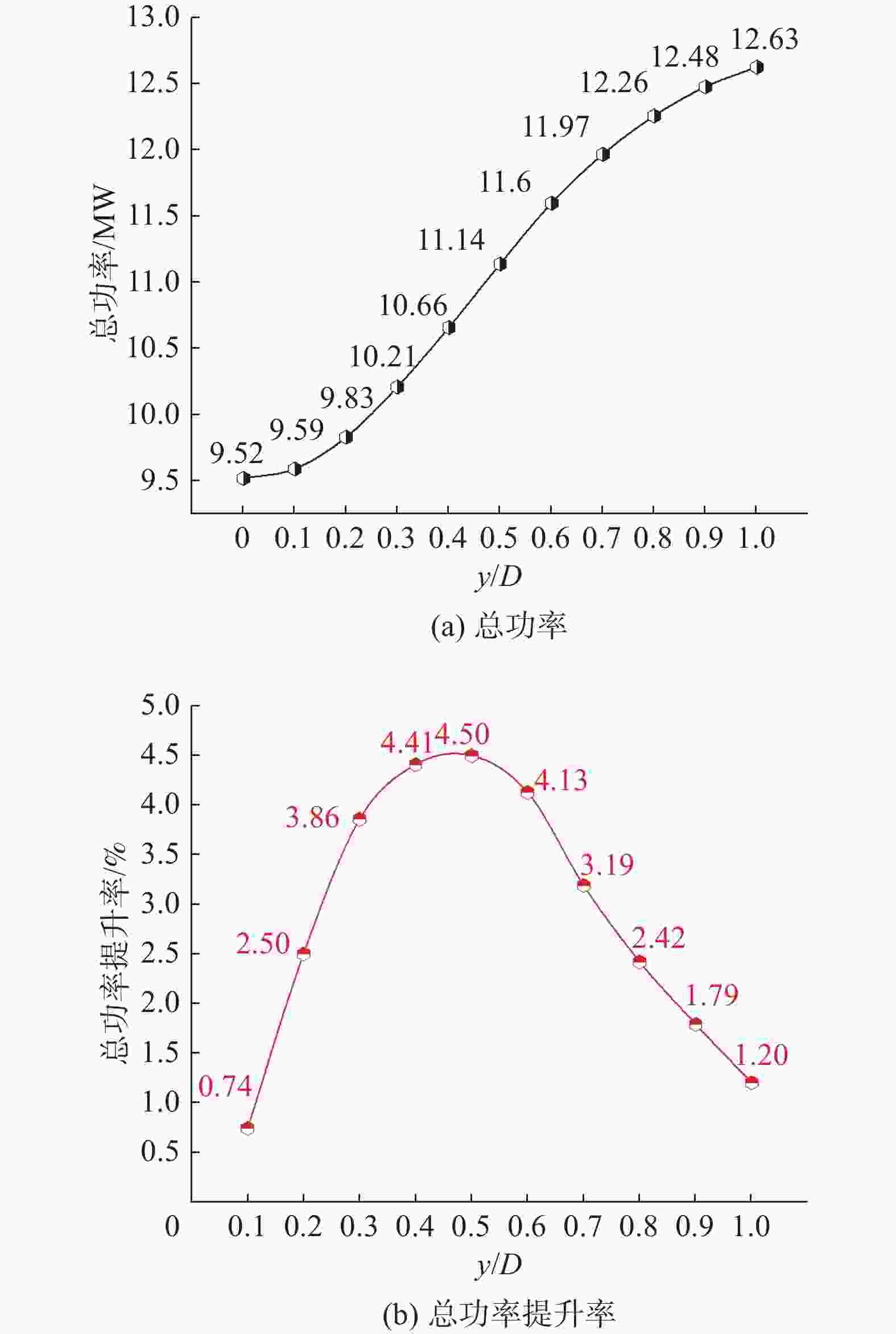
图 14 T2风机位置优化后不同横向间距下总功率及其提升率对比图
Figure 14. Comparison of the total power and its improvement rate under different lateral spacing after the optimization of the position of T2 wind turbine
当T1风机与T3风机纵向距离为10D，且T2风机横向错列距离为0.5D时，改变T2与T1风机的纵向间距，分析风电场功率变化情况。由图15可知，功率变化情况与图10中的功率变化情况有所不同。风电场功率最大时T2风机所处位置并未在距T1风机4D处，而是随T2风机与T1风机纵向距离的增大而减小。这是由于T2风机相当于T1风机进行了错列，使得其受T1风机的尾流影响有所减弱，风机间纵向间距对输出功率的影响更加明显。当T2风机与T1风机纵向间距为2D时，风电场总功率达最大值，此时T3风机输出功率占总功率的30.31%；纵向间距为8D时，T3风机输出功率占比下降至25.55%。当T2风机逐渐靠近T3风机时，T3风机的功率逐渐减小，风电场总功率也逐渐下降。这表明改变风机间纵向间距时，T2更宜靠近T1风机。这也进一步验证了通过牺牲前排风机的输出功率来提高后排风机的输出功率的方法对于提高风电场输出功率是可行的。
图 15 T2风机错列0.5D时风电场总功率变化情况
Figure 15. The change of the total power of the wind farm when the T2 wind turbine is staggered by 0.5D
-
文章旨在研究三风机的发电效率优化布置，对不同布置方式下风电场功率变化情况进行了分析，从后排风机的输出功率入手，分析了风机位置变化对风电场总功率的影响，并得到以下几点结论：
1）串列三风机随着风机纵向间距的增大，后排风机功率呈现不同幅度的增长，风电场功率提升率呈先增后减再增加的趋势。特别是当风机纵向间距由4D增大到5D及10D增大到11D时，风电场的总功率提升率较大，分别为8.64%和9.83%。
2）风机间纵向间距为5D时，随着T1与T2风机横向间距的增加，后排风机的功率增长速率大致相同，但在横向间距为0.4D～0.6D范围内其增长速率提升幅度较大，即在此范围内风电场的布局优化效果较好。
3）分析T2风机在不同工况下对于风电场总功率的影响情况可以发现，当风电场大小固定时，在三风机串列条件下，风电场中风机宜均匀布置；错列条件下，中游风机宜靠近上游风机。
Optimization of Aerodynamic Power of Three Wind Turbines in Turbulent Wind Farm
-
摘要:
目的 在全球能源结构转型和气候变化应对的大背景下，风能作为清洁、可再生的能源之一，其利用效率的优化已成为当前能源领域研究的重点。为减小因风机间尾流效应对风电场输出功率的影响，提高风电场效率，对风机进行合理布局是很有必要的。 方法 运用Fast Farm模拟技术，分别研究了串列以及错列布置下随着风机间间距的改变对于湍流风场中3台NREL 5 MW风机输出功率及功率提升率的变化情况。 结果 当风机间间距增大时，可以明显提升后排风机的输出功率，但其提升程度有所不同，其中，当风机纵向间距由5D增加到6D及10D增加到11D时，可使风电场发电量得到较大提升；对于风机间横向间距在合理取值范围内，可使得风电场布局达到最优。 结论 文章对风机间间距进行了较为详细的划分，通过不同工况下对风电场功率影响程度分析可知在串列及错列条件下对于风机的优化布局存在差异，为风电场的布局优化提供了一定的参考。 Abstract:Objective In the context of global energy structure transformation and climate change response, wind energy, as one of the clean and renewable energy sources, the optimization of its utilization efficiency has become the focus of current research in the energy field. In order to reduce the influence of the wake effect between wind turbines on the output power of wind farms and improve the efficiency of wind farms, it is necessary to carry out a reasonable layout of wind turbines. Method Using Fast Farm simulation technology, the effects of changing the wind turbine spacing on the power and its improvement rate of three NREL 5 MW turbines in a turbulent wind farm under tandem and staggered arrangements were studied. Result When the spacing between turbines increases, the output power of the rear turbines can be significantly improved, but the degree of improvement is different, in which when the longitudinal spacing of the turbines is increased from 5D to 6D and from 10D to 11D, the power generation of the wind farm can be greatly improved. A reasonable range of values for the lateral spacing between wind turbines is derived, which allows for an optimal layout of the wind farm. Conclusion In this paper, the spacing between wind turbines is divided in more detail, and through the analysis of the degree of impact on the power of wind farms under different conditions, it can be seen that there are differences in the optimization of the layout of the wind turbine under the conditions of series and staggered rows, which provides a certain reference for the optimization of the layout of wind farms. -
Key words:
- turbulent wind /
- three wind turbines /
- optimal layout /
- wind turbine spacing /
- power improvement rate
-
图 2 文章计算结果与Kaimal谱对比图
Fig. 2 Comparison between the simulated wind speed spectrum and the Kaimal spectrum
图 3 文章计算结果与SCADA实测数据对比情况
Fig. 3 Comparison between the calculated results in this paper and the measured data of SCADA
图 6 纵向间距L=5D三风机群计算模型示意图
Fig. 6 Schematic diagram of the calculation model of the longitudinal spacing L=5D three-wind turbines
图 7 不同纵向间距下后排风机输出功率
Fig. 7 Output power of rear exhaust wind turbines under different longitudinal spacings
图 8 不同纵向间距下总功率及其提升率对比图
Fig. 8 Comparison of total power and its improvement rate at different vertical spacings
图 9 不同纵向间距风电场速度分布
Fig. 9 Speed distribution map of wind farms with different longitudinal spacings
图 10 T2风机在不同纵向间距下风电场总功率变化情况
Fig. 10 Change in the total power of wind farms under different longitudinal spacings of T2 wind turbine
图 11 不同横向间距下后排风机输出功率
Fig. 11 The output power of the rear wind turbine at different lateral spacings
图 12 不同横向间距下总功率及其提升率对比图
Fig. 12 Comparison of total power and its improvement rate under different lateral spacings
图 13 横向间距0.5D风电场速度分布图
Fig. 13 Velocity distribution of wind farm at a horizontal spacing of 0.5D
图 14 T2风机位置优化后不同横向间距下总功率及其提升率对比图
Fig. 14 Comparison of the total power and its improvement rate under different lateral spacing after the optimization of the position of T2 wind turbine
图 15 T2风机错列0.5D时风电场总功率变化情况
Fig. 15 The change of the total power of the wind farm when the T2 wind turbine is staggered by 0.5D
表 1 不同网格尺寸下单风机功率对比
Tab. 1. Comparison of the power of the single wind turbine at the different grid sizes
工况 低分辨率计算域
网格大小/m高分辨率计算域
网格大小/m风机功率/
MW功率
对比率/%Mesh1 10 5 5.28 99.81 Mesh2 10 10 5.23 98.87 Mesh3 20 10 5.22 98.68 
下载: 导出CSV
表 2 算例参数设置统计表
Tab. 2. Example parameter setting statistical table
算例编号 排布方式 纵向间距 第二台风机错列距离 1 串列布置 2D～11D 0 2 错列布置 2D～11D 0～1D
下载: 导出CSV
-
[1] VEERS P, DYKES K, LANTZ E, et al. Grand challenges in the science of wind energy [J]. Science, 2019, 366(6464): eaau2027. DOI: 10.1126/science.aau2027. [2] DETHLEFF D, WEINRICH N, KOWALD B, et al. Air medical evacuations from the German North Sea wind farm bard offshore 1: traumatic injuries, acute diseases, and rescue process times (2011-2013) [J]. Air medical journal, 2016, 35(4): 216-226. DOI: 10.1016/j.amj.2016.02.002. [3] FRANDSEN S, BARTHELMIE R, PRYOR S, et al. Analytical modelling of wind speed deficit in large offshore wind farms [J]. Wind energy, 2006, 9(1/2): 39-53. DOI: 10.1002/we.189. [4] ARCHER C L, VASEL-BE-HAGH A, YAN C, et al. Review and evaluation of wake loss models for wind energy applications [J]. Applied energy, 2018, 226: 1187-1207. DOI: 10.1016/j.apenergy.2018.05.085. [5] LUBITZ W D. Impact of ambient turbulence on performance of a small wind turbine [J]. Renewable energy, 2014, 61(3): 69-73. DOI: 10.1016/j.renene.2012.08.015. [6] PORTÉ-AGEL F, WU Y T, LU H, et al. Large-eddy simulation of atmospheric boundary layer flow through wind turbines and wind farms [J]. Journal of wind engineering and industrial aerodynamics, 2011, 99(4): 154-168. DOI: 10.1016/j.jweia.2011.01.011. [7] BARTHELMIE R J, RATHMANN O, FRANDSEN S T, et al. Modelling and measurements of wakes in large wind farms [J]. Journal of physics: conference series, 2007, 75(1): 012049. DOI: 10.1088/1742-6596/75/1/012049. [8] CARCANGIU C E. CFD-RANS study of horizontal axis wind turbines [D]. Cagliari: Università degli Studi di Cagliari, 2008. [9] 陈默, 张璇, 郑文涛, 等. 风电场尾流干涉效应及布局优化研究 [J]. 科学技术与工程, 2023, 23(36): 15491-15497. DOI: 10.3969/j.issn.1671-1815.2023.36.018. CHEN M, ZHANG X, ZHENG W T, et al. Wake interference effect and layout optimization of wind farm [J]. Science technology and engineering, 2023, 23(36): 15491-15497. DOI: 10.3969/j.issn.1671-1815.2023.36.018. [10] 张周周, 陈建, 徐洪涛, 等. 升力型垂直轴风力机相互作用研究 [J]. 中国机械工程, 2017, 28(21): 2577-2581, 2587. DOI: 10.3969/j.issn.1004-132X.2017.21.011. ZHANG Z Z, CHEN J, XU H T, et al. Investigation of interaction between lift-type VAWTs [J]. China mechanical engineering, 2017, 28(21): 2577-2581, 2587. DOI: 10.3969/j.issn.1004-132X.2017.21.011. [11] 李少华, 岳巍澎, 匡青峰, 等. 双机组风力机尾流互扰及阵列的数值模拟 [J]. 中国电机工程学报, 2011, 31(5): 101-107. DOI: 10.13334/j.0258-8013.pcsee.2011.05.019. LI S H, YUE W P, KUANG Q F, et al. Numerical simulation of wake interaction and array of double wind turbine [J]. Proceedings of the CSEE, 2011, 31(5): 101-107. DOI: 10.13334/j.0258-8013.pcsee.2011.05.019. [12] 田琳琳, 赵宁, 钟伟. 风力机尾流相互干扰的数值模拟 [J]. 太阳能学报, 2012, 33(8): 1315-1320. DOI: 10.19912/j.0254-0096.2012.08.011. TIAN L L, ZHAO N, ZHONG W. Numerical simulation of wake interactions of wind turbines [J]. Acta energiae solaris sinica, 2012, 33(8): 1315-1320. DOI: 10.19912/j.0254-0096.2012.08.011. [13] 郭静婷. 风电场中风力机间相互影响的研究 [D]. 呼和浩特: 内蒙古工业大学, 2010. GUO J T. Research on optimization collocation in wind farm [D]. Hohhot: Inner Mongolia University of Technology, 2010. [14] 蔡新, 潘盼, 朱杰, 等. 基于CFD技术的垂直轴风力机动态尾流特性研究 [J]. 计算力学学报, 2014, 31(5): 675-680. DOI: 10.7511/jslx201405022. CAI X, PAN P, ZHU J, et al. Analysis of vertical axis wind turbine dynamic wake with CFD technology [J]. Chinese journal of computational mechanics, 2014, 31(5): 675-680. DOI: 10.7511/jslx201405022. [15] WU Y T, LIAO T L, CHEN C K, et al. Power output efficiency in large wind farms with different hub heights and configurations [J]. Renewable energy, 2019, 132: 941-949. DOI: 10.1016/j.renene.2018.08.051. [16] ZHAO C Y, ZHANG Z J. Digital filter design and performance analysis of dynamic temperature signal denoise based on FPGA [C]//Proceedings of the 10th International Conference on Sensing Technology, Nanjing, China, November 11-13, 2016. Nanjing: IEEE, 2016: 71-74. DOI: 10.1109/ICSensT.2016.7796285. [17] 张思瑶, 赵超, 隋东, 等. 风电场流场特性及风机布局数值模拟研究 [J]. 气象与环境学报, 2021, 37(2): 101-106. DOI: 10.3969/j.issn.1673-503X.2021.02.014. ZHANG S Y, ZHAO C, SUI D, et al. Research on numerical simulation of wind farm flow field characteristics and fan layout [J]. Journal of meteorology and environment, 2021, 37(2): 101-106. DOI: 10.3969/j.issn.1673-503X.2021.02.014. [18] MOSETTI G, POLONI C, DIVIACCO B. Optimization of wind turbine positioning in large windfarms by means of a genetic algorithm [J]. Journal of wind engineering and industrial aerodynamics, 1994, 51(1): 105-116. DOI: 10.1016/0167-6105(94)90080-9. [19] GRADY S A, HUSSAINI M Y, ABDULLAH M M. Placement of wind turbines using genetic algorithms [J]. Renewable energy, 2005, 30(2): 259-270. DOI: 10.1016/j.renene.2004.05.007. [20] 徐佳楠, 张天瑞, 李玉龙. 基于自适应遗传-粒子群优化算法的风电场微观选址优化 [J]. 科学技术与工程, 2023, 23(16): 6917-6922. DOI: 10.3969/j.issn.1671-1815.2023.16.023. XU J N, ZHANG T R, LI Y L. Micro-location and optimization of wind farm based on the adaptive GA-PSO algorithm [J]. Science technology and engineering, 2023, 23(16): 6917-6922. DOI: 10.3969/j.issn.1671-1815.2023.16.023. [21] SHALER K, JONKMAN J, HAMILTON N. Effects of inflow spatiotemporal discretization on wake meandering and turbine structural response using FAST. Farm [J]. Journal of physics: conference series, 2019, 1256: 012023. DOI: 10.1088/1742-6596/1256/1/012023. [22] 崔家平. 考虑尾流效应的漂浮式风电场出力控制策略研究 [D]. 沈阳: 沈阳工业大学, 2022. DOI: 10.27322/d.cnki.gsgyu.2022.000059. CUI J P. Research on power output control strategy of floating wind farm considering wake effect [D]. Shenyang: Shenyang University of Technology, 2022. DOI: 10.27322/d.cnki.gsgyu.2022.000059. [23] GAUMOND M, RÉTHORÉ P E, OTT S, et al. Evaluation of the wind direction uncertainty and its impact on wake modeling at the horns rev offshore wind farm [J]. Wind energy, 2014, 17(8): 1169-1178. DOI: 10.1002/we.1625. [24] 吴俊. 海上浮式风力机气动性能的数值模拟 [D]上海: 上海交通大学, 2016. DOI: 10.27307/d.cnki.gsjtu.2016.000283. WU J. Numerical analysis of aerodynamic performance of floating offshore wind turbine [D]. Shanghai: Shanghai Jiao Tong University, 2016. DOI: 10.27307/d.cnki.gsjtu.2016.000283. [25] 刘强, 杨科, 黄宸武, 等. 5 MW大型风力机气动特性计算及分析 [J]. 工程热物理学报, 2012, 33(7): 1155-1159. LIU Q, YNGA K, HUNAG C W, et al. Simulation and analysis of the aerodynamic characteristics of a 5 MW wind turbine [J]. Journal of engineering thermophysics, 2012, 33(7): 1155-1159. [26] 艾勇. 基于致动线模型的风电场复杂尾流特性研究 [D]. 上海: 上海交通大学, 2018. DOI: 10.27307/d.cnki.gsjtu.2018.000067. AI Y. Numerical simulation of complex wake flows for wind farm based on actuator line model [D]. Shanghai: Shanghai Jiao Tong University, 2018. DOI: 10.27307/d.cnki.gsjtu.2018.000067. [27] CHOWDHURY S, ZHANG J, MESSAC A, et al. Unrestricted wind farm layout optimization (UWFLO): investigating key factors influencing the maximum power generation [J]. Renewable energy, 2012, 38(1): 16-30. DOI: 10.1016/j.renene.2011.06.033. [28] 胡丹梅, 郑筱凯, 张建平. 风力机不同排列方式下尾迹数值模拟 [J]. 可再生能源, 2015, 33(5): 684-692. DOI: 10.13941/j.cnki.21-1469/tk.2015.05.007. HU D M, ZHENG X K, ZHANG J P. Wake numerical simulation of wind turbine in different arrangement [J]. Renewable energy resources, 2015, 33(5): 684-692. DOI: 10.13941/j.cnki.21-1469/tk.2015.05.007. -
计量
- 文章访问数: 55
- HTML全文浏览量: 33
- PDF下载量: 4
- 被引次数: 0
