-
近年来，随着环境污染问题的日益加剧以及对化石燃料危机的日益担忧，为减少碳排放，改善空气质量，响应国家碳达峰碳中和的号召，电动汽车（Electric Vehicle，EV）越来越受重视[1]。根据美国交通统计调查公布的调查数据，电动汽车每天行驶在路上的时间只占全天的4%～5%，随着电动汽车数目的增多，电动汽车储能量急剧增加[2]。除此之外，截至2023年，中国的电动汽车保有量已经超过
1600 万辆，占全球电动汽车总量的60%以上，这使中国成为全球最大的电动汽车市场。2023年，中国电动汽车的用电量占全国总用电量的比例为2%，这一比例在城市和高电动汽车普及率地区更高。例如，在上海、深圳等城市，电动汽车的用电量已经成为城市电网负荷的重要组成部分。若能将此部分能量与电网形成有效的交互传递，将会产生难以想象的巨大经济及社会效益，实现对电网能量的“削峰填谷”，增强电网韧性与稳定性，实现对能源的均衡性利用[3]。因此，V2G（Vehicle to Grid）技术应运而生。V2G是指电动汽车与电网之间的双向能量交换技术，其核心在于考虑无功功率响应的电动汽车充放电调度策略。该技术的基础是能够实现能量双向转换的电力电子变换器及其相应的控制策略[4]。目前，有大量学者针对V2G变换器拓扑及控制策略开展研究[5-8]，文献[9-10]提出两种可应用于V2G系统的变换器电路拓扑及控制策略，并利用MATLAB/Simulink仿真软件对其可行性进行说明。文献[11]提出一种双有源桥变换器参数设计优化方法，结合频率、输出电压范围、输入输出电压匹配关系等优化双有源桥逆变器的参数，提升了双有源桥逆变器的效率。在变换器控制策略方面，相较于P/Q控制及U/f控制，下垂控制及VSG（Virtual Synchronous Generator）控制不存在线路末端电压质量差、容量需求大、变换器之间需要进行通信等缺点，故下垂控制及VSG控制更适用于V2G系统[12-15]。文献[16]对比电压与电流型VSG控制，发现较之于电流型VSG控制，电压型VSG控制更易于稳定，适用于超弱电网中并网可再生能源发电。文献[17]通过对传统VSG控制进行改进，提出一种基于自适应旋转惯量的VSG控制策略，通过仿真验证了新的控制策略具有更好的稳定性及响应速度等。
在充放电调度策略方面，目前的研究热点是有功功率的控制[18-20]，文献[21]通过建立电动汽车多目标优化模型研究了分时电价调度策略对电网运行及用户的影响。文献[22-23]研究了计及电池损耗的电动汽车分层调度策略，降低了电池损耗及成本，减小了负荷波动。文献[24-25]建立了考虑电动汽车聚合商、车主动态行为等多种因素的调度策略。然而目前的研究大多以有功功率控制为主，对电动汽车充放电过程中无功功率的分配与优化调度研究不足，且未将电动汽车充电站与电网联系起来进行协同调度优化。因此有必要将有功及无功考虑在内，研究二者交互的调度策略，实现对电动汽车充电站储能的应用，发挥其削峰填谷，促进可再生能源消纳，增强电网稳定性的作用。
此外，现有的系统调度策略与充电站功率变换器的控制策略尚未形成交互。针对这个问题，文章建立了一种面向新型电力系统的双层滚动优化调度模型，该模型可根据用户提交信息制定最优充放电计划。为确保各充电站充放电计划的实施，采用改进的VSG控制策略对充电站内的功率变换器进行控制，并与上层的滚动优化调度策略相结合，以实现功率调度。经验证，通过以上调度控制策略配合降低了负荷峰谷差，改善了系统电压水平。
文章根据目前研究论文大量阐述充放电策略以及V2G变换器控制策略，但并未提及两者配合联系的研究现状，提出两者相互配合的观点，能够提高电网稳定性。
-
随着电动汽车数量的不断增加，电动汽车的能源调度策略对电网稳定性的影响日益显著。然而，为每辆电动汽车单独制定调度计划显然不切实际。因此，可以通过分时电价来引导用户选择充放电时段，从而实现分群调度。
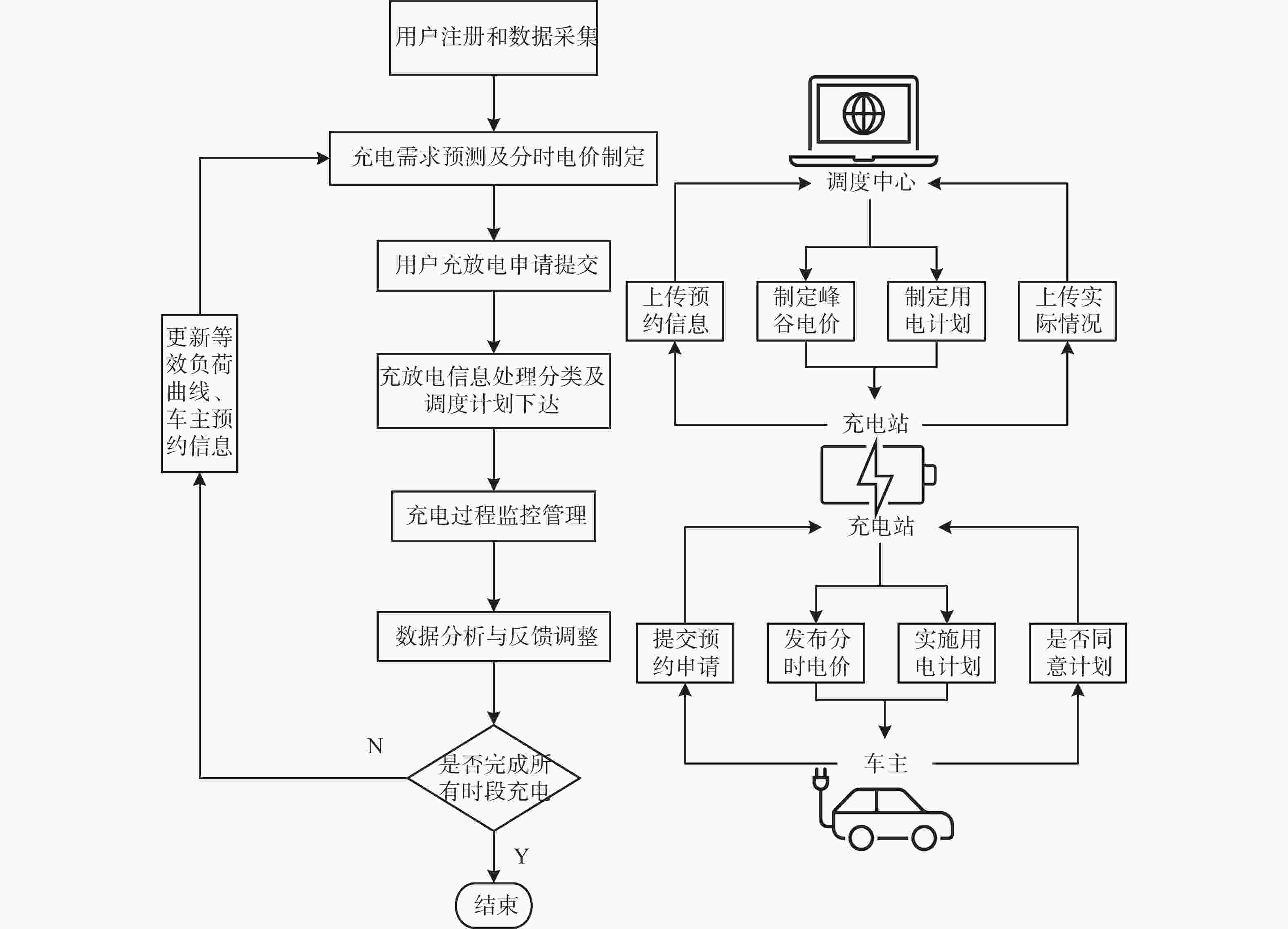
同时，在智能电网技术的支持下，可以实现用户、调度中心和电网之间的信息交互，并通过日前申请机制进行电动汽车的充放电调度。具体方案流程如图1所示。
图 1 V2G调度流程
Figure 1. V2G scheduling process
从图1中可以看出V2G调度流程为根据用户注册和数据采集的信息，对充放电需求进行预测并制定分时电价。在此基础上，通过分析用户提交的申请数据，以及检查是否完成充放电来更新等效负荷曲线。随后，再根据车主的预约信息对充放电需求预测和分时电价进行进一步调整和更新。
通过这种综合的优化调度策略，可以有效地提高充电站运营效率，平衡电网负荷，同时满足电动汽车用户的需求。这种方法将对未来的智能电网和电动汽车充电基础设施的发展起到积极的推动作用。但有以下3点需要进行说明：
1）以上调度策略只针对提交申请的用户，其他未上传信息的用户按传统负荷进行处理。
2）以上调度策略需要电动汽车充电站可实现电动汽车的充电与放电，即仅适用于V2G系统。
3）文章仅研究预约信息提供后功率的优化分配及结合超短期预测和当前时段数据等更新车主预约信息及重新分配各充电站功率问题。
-
为实现错峰填谷，增强V2G系统运行稳定性与经济性的目标，在以上调度框架下，建立双层滚动优化模型对能源进行合理分配。该模型主要分为双层优化电动汽车充放电调度模型及滚动优化策略。
-
该模型主要分为2层，上层为实时调度层，下层为功率分配层。
1）实时调度层
对于实时功率调度，使用超短期预测对日前预约的负荷曲线进行修正，并以最小化峰谷差为目标来优化电动汽车的充放电功率分配。由此可得本层的目标函数如下：
$$ \min f = \frac{1}{T}{\sum\limits_{t = 1}^T {[{P_{\mathrm{L}}}(t) - {P_{{\mathrm{DG}}}}(t) + {P_{{\mathrm{EV}}}}(t) - \bar P]} ^2} $$ (1) 式中：
T −总时段（h）；
PL(t) −t时段基础负荷消耗的平均功率（W）；
PDG(t) −t时段分布式新能源发电发出功率（W）；
PEV(t) −t时段电动汽车充放电功率（W）；
$ \bar P $ −等效负荷平均值（W）。
同时，以上函数需满足以下几个约束：
系统功率平衡：
$$ {P_{{\mathrm{DG}}}}(t) + {P_{{\mathrm{grid}}}}(t) = {P_{\mathrm{L}}}(t) + {P_{{\mathrm{loss}}}}(t) + {P_{{\mathrm{EV}}}}(t) $$ (2) 式中：
Pgrid(t) −t时刻网络传输的有功功率（W）；
Ploss(t) −有功网损（W）。
电动汽车电池容量限制：
$$ \left|P_{\mathrm{EV}}\left(t_{{\mathrm{c}}}\right)\right| \leqslant\left|\sum_{n=1}^{N_{{\mathrm{c}}}} C_{\mathrm{EV}}(n)\right| $$ (3) $$ \left| {\sum\limits_{t \in {T_{{\text{inl}}}}} {{P_{{\mathrm{EV}}}}(t)} } \right| \leqslant \left| {\sum\limits_{n = 1}^{{N_{{\text{inl}}}}} {{C_{{\mathrm{EV}}}}(n)} } \right| $$ (4) 式中：
PEV(tc) −当前时段（实时）电动汽车的调度功率（W），当电动汽车充电为正，电动汽车放电为负；
Nc −当前预约信息中的电动汽车数量（辆），此申请时段包含当前时段；
Tinl −某一电价区间所包含的所有时段的集合；
Ninl −申请时段在该电价区间内的电动汽车数量；
CEV(n) −第n辆电动汽车的申请充放电量（Wh），当申请充电为正，申请放电为负。
电动汽车充放电功率限制：
$$ - P_{{\mathrm{disc}},\; \max }^{} \leqslant {P_{{\mathrm{EV}}}}(t) \leqslant P_{{\text{char},\; \max}}^{} $$ (5) 式中：
Pdisc, max −电动汽车最大放电功率（W）；
Pchar, max −电动汽车最大充电功率（W）。
分布式新能源发电量限制：
$$ P_{{\mathrm{DG}},\; \min }^{} \leqslant {P_{{\mathrm{DG}}}}\left( t \right) \leqslant P_{{\mathrm{DG}},\; \max }^{} $$ (6) 式中：
PDG, min、PDG, max−分布式新能源发出有功功率的最小及最大值（W）。
配电变压器传输容量限制：
$$ P_{{\mathrm{grid}},\; \min }^{} \leqslant {P_{{\mathrm{grid}}}}\left( t \right) \leqslant P_{{\mathrm{grid}},\; \max }^{} $$ (7) 式中：
Pgrid, min、Pgrid, max−配电变压器的有功传输容量的最小及最大值（W）。
2）功率分配层
根据上层的优化结果，可得本时段所有预约电动汽车最优的功率分配，故本层需要对充放电的有功及无功功率输出进行优化，以实现系统网损最低为目标，如式（8）所示：
$$ \min f=\sum_{k=1}^{N_{{\mathrm{b}}}}\left[r_{k} I_{k}(t)^{2}\right] \Delta t $$ (8) 式中：
rk −第k条支路的电阻（Ω）；
Ik(t) −t时刻支路k上流过的电流（A）；
∆t −该时段长度（h）；
Nb −系统中总的支路数目。
在下层模型中，以上目标函数存在以下约束：
电动汽车电池容量限制：
$$ \left| {{P_{{\mathrm{stg}}}}(m,{t_{\mathrm{c}}})} \right| \leqslant \left| {\sum\limits_{n = 1}^{{N_{{\mathrm{m,c}}}}} {{C_{{\mathrm{EV}}}}(n)} } \right| $$ (9) 式中：
Pstg(m,tc) −tc时段，充电站m的输出功率（W）；
Nm, c −该时段本电站申请充放电电动车数目；
CEV(n) −电动汽车申请充放电量（Wh）。
充电站充放电功率限制：
$$ - P_{{\mathrm{m.disc}},\; \max }^{} \leqslant {P_{{\mathrm{stg}}}}\left( {m,t} \right) \leqslant P_{{\text{m}}{\text{.char},\; \max}}^{} $$ (10) 式中：
Pm.disc, max、Pm.char, max−第m个电动汽车充电站最大、最小充放电功率（W）。
上层模型功率限制：
$$ \sum\limits_{m = 1}^{{N_{{\mathrm{stg}}}}} {{P_{{\mathrm{stg}}}}(m,t)} = {P_{{\mathrm{EV}}}}(t) $$ (11) 式中：
PEV(t) −上层模型优化后得到的电动汽车充放电功率（W）。
双向换流器通流能力限制：
$$ P_{{\mathrm{stg}}}^2 \leqslant Q_{{\mathrm{stg}}}^2 \leqslant S_{{\mathrm{stg}}.\max }^2 $$ (12) 节点电压及线路电流约束：
$$ \begin{gathered} V_{{j},\; \min }^{} \leqslant {V_{j}}(t) \leqslant V_{{j},\; \max }^{} \\ {I_k}(t) \leqslant {I_{k, \; \max }} \\ \end{gathered} $$ (13) 式中：
Vj, min、Vj, max −节点j允许的电压上下限值（V）；
Ik, max −线路k允许流过的最大电流值（A）。
系统潮流约束：
$$ \begin{split}& \sum_{i \in m(j)}\left[P_{i j}(t)-r_{i j} I_{i j}(t)^2\right]=\sum_{k \in n({j})} P_{j k}(t)+P_{j}(t) \\& \sum_{i \in m({j})}\left[Q_{i j}(t)-x_{i j} I_{i j}(t)^2\right]=\sum_{k \in n({j})} Q_{j k}(t)+Q_{j}(t) \\& V_{j}(t)^2=V_i(t)-2\left[r_{i j} P_{i j}(t)+x_{i j} Q_{i j}(t)\right]+\left(r_{i j}^2+x_{i j}^2\right) I_{i j}(t)^2 \\& I_{i j}(t)^2=\frac{P_{i j}(t)^2+Q_{i j}(t)^2}{V_{i}(t)^2} \\[-2pt] \end{split}$$ (14) 式中：
m(j)、n(j)——包含节点j的支路集合；
Pij、Pjk ——对应线路上传输的有功功率（W）；
Qij、Qjk ——对应线路上传输的无功功率（Var）；
Pj −节点j的净有功负荷（W）；
Qj −节点j的净无功负荷（Var）；
rij、xij −线路的电阻、电抗（Ω）；
Iij −线路上传输的电流（A）；
Vi、Vj −节点i、j的电压（V）。
以上约束可化为线性约束及二阶锥约束，可通过二阶锥规划求解以上模型。
-
由于负荷预测值与实际值之间可能存在差异，电动汽车申请充放电量与实际充放电量也存在差异，因此若完全按照以上模型进行能源调度与优化可能使得调度计划与实际功率分配产生较大出入，使得功率分配不合理，造成能源浪费。因此，可加入反馈环节进行滚动优化调度，具体优化流程如下：
1）考虑到当日可再生能源的产出能力以及电力需求的变化，结合前一时间段的数据、超短期和日前预测情况，以及车主预定的信息，实时优化调度系统将对今日余下时间内电动汽车的充电和放电功率进行调整，确定系统在当前时间段内最佳充放电功率。
2）在配电环节，参照各充电站的预约信息，以实时调度层输出等效负荷曲线为限制条件，合理安排每个充电站电动汽车的充放电功率。同时，考虑双向变流器容量限制，对各个充电站的无功功率的数值和方向进行精细调整。
3）对于接下来的时间段，将更新先前的数据、超短期以及日前的预测信息，同时也更新各个充电站车主的预约情况。按照这一流程反复操作，直到完成当日的所有时段调度为止。
-
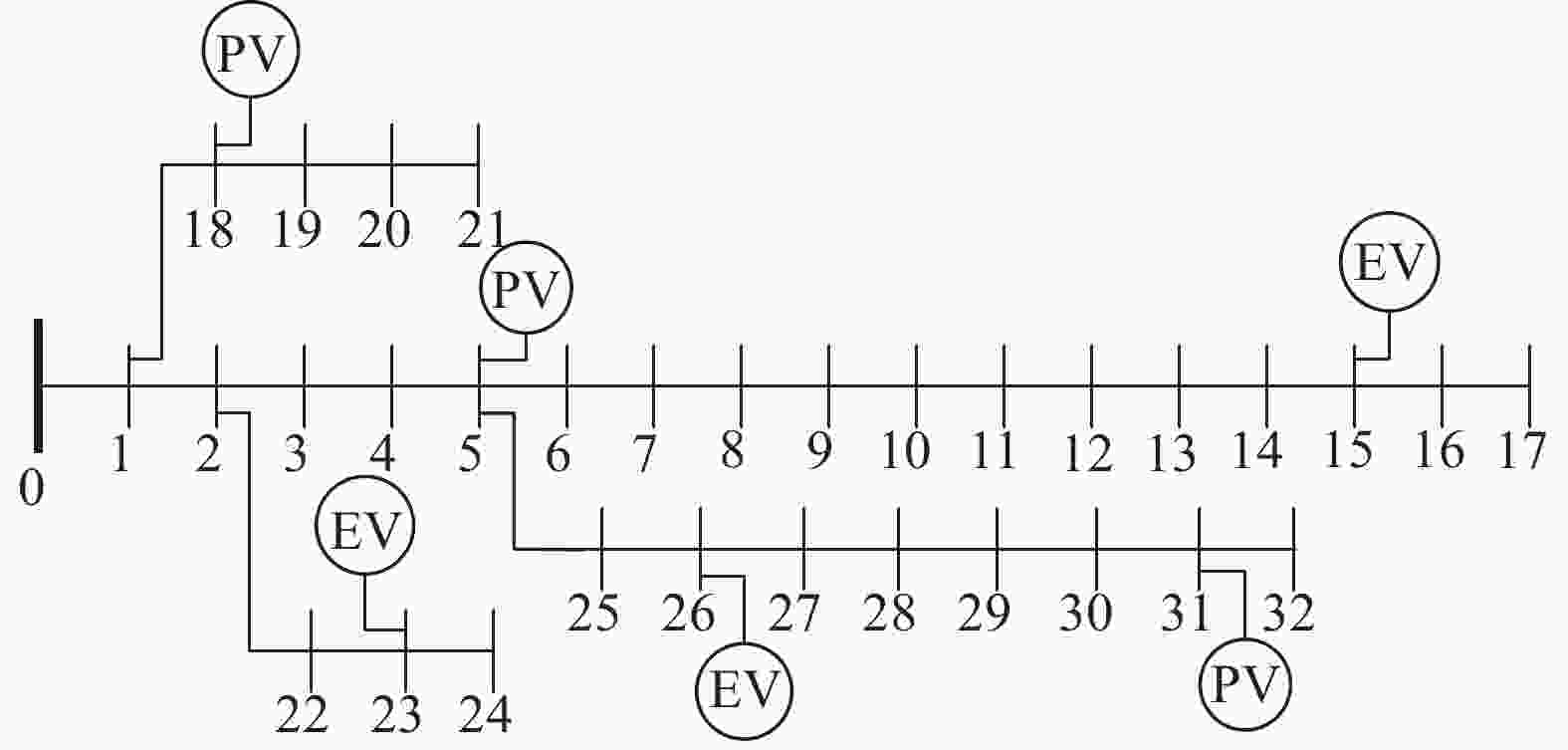
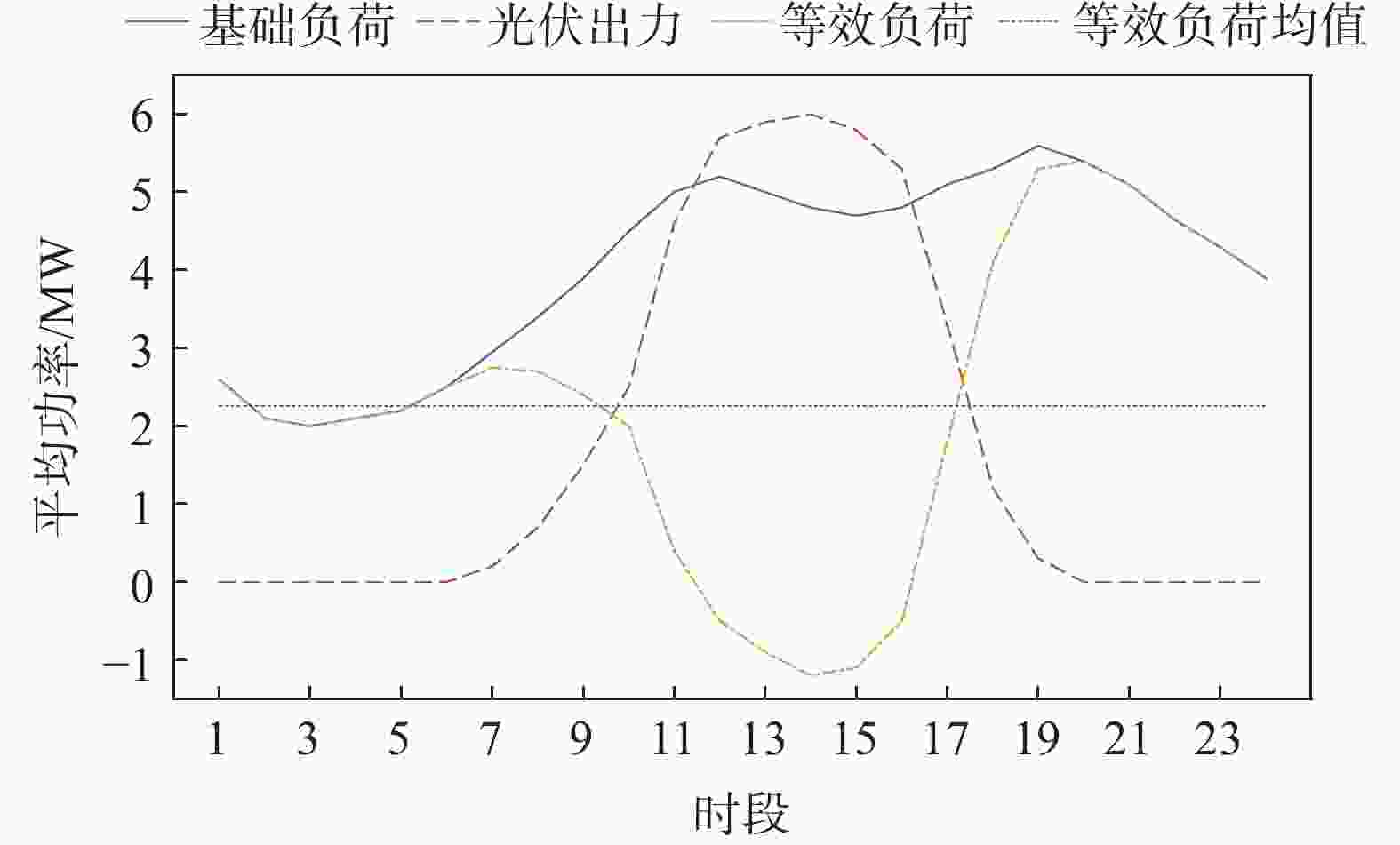
文章以IEEE33节点系统为例，改进系统拓扑结构如图2所示，其中PV（Photovoltaic）是光伏发电。假设新能源分布式发电站接入到5、18、31节点，装机容量分别为2.5 MW、2 MW、2.5 MW，功率因数为0.95，恒功率并网。电动汽车充电站分布于15、23、26节点。电动汽车充电站采用集中式换流器并网，换流器为双向功率变换器，控制方式采用下文所述改进VSG控制，Smax为0.6 MVA。系统UN=12.66 kV，SN=10 MVA，Ik, max=500 A。假设某日日前负荷预测数据以及光伏申请出力计划如图3所示[26]，根据图3可知，根据等效负荷曲线，10:00－17:00最低，18:00－24:00最高，因此假设以上时段预约信息如表1所示。
图 2 仿真系统拓扑结构
Figure 2. Simulation system topology
图 3 某日光伏、负荷功率预测曲线
Figure 3. Photovoltaic and load power prediction curve for a certain day
表 1 各充电站预约信息
Table 1. Appointment information for each charging station
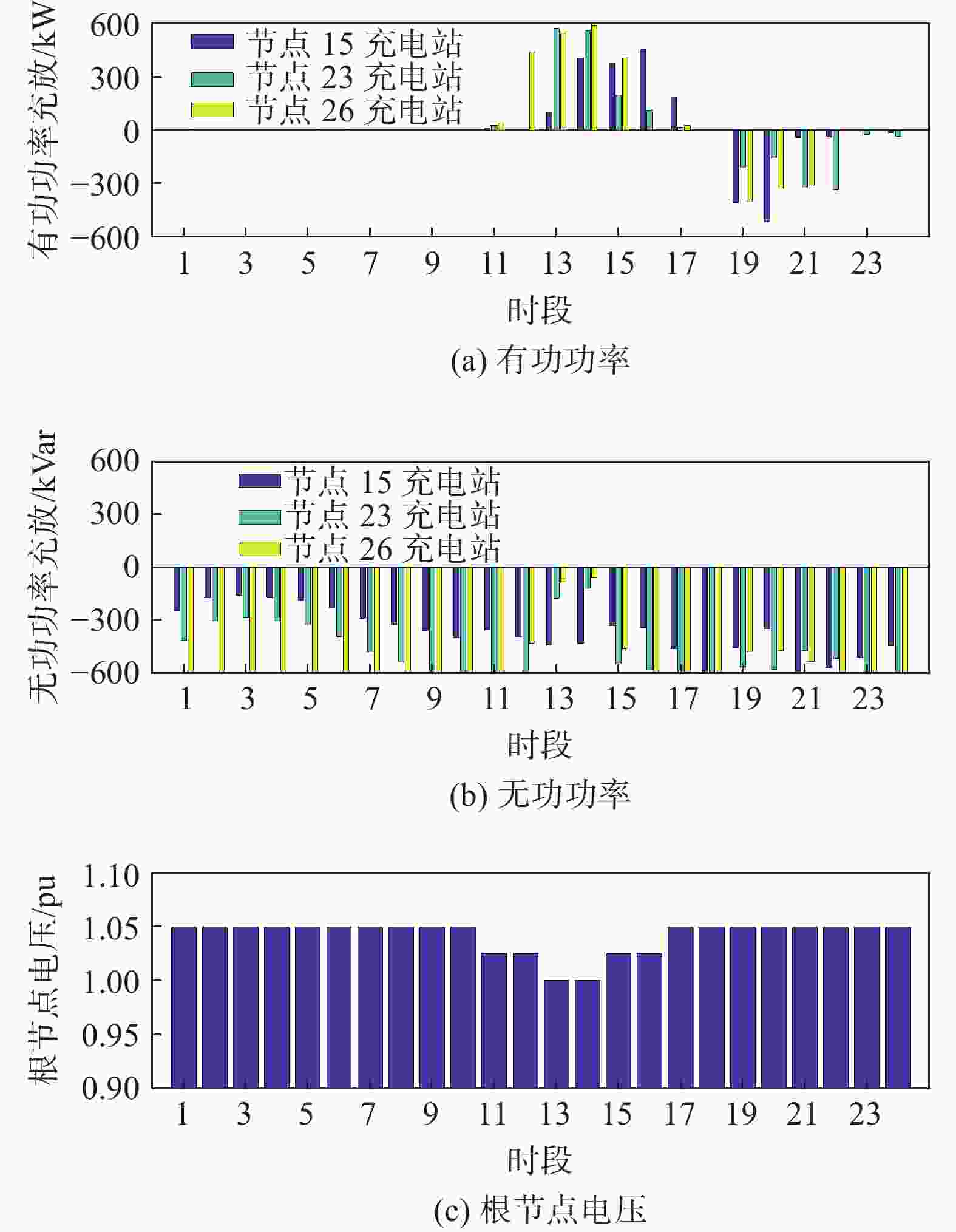
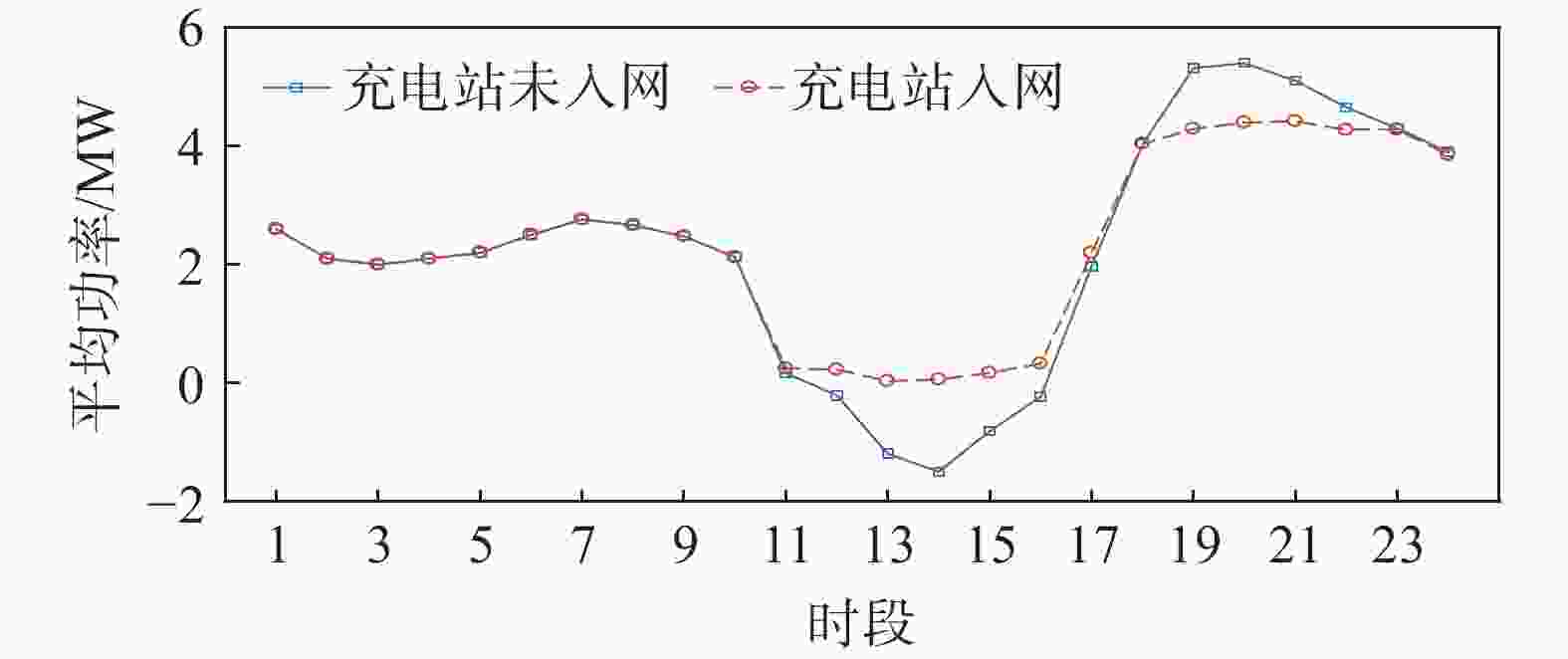
时段 各充电站时段容量限制/kW 节点15充电站 节点23充电站 节点26充电站 1 155 190 165 2 185 165 170 3 185 190 225 4 190 200 225 5 255 350 195 6 335 455 355 7 310 295 300 8 425 455 395 9 525 515 495 10 335 295 285 11 255 195 280 12 735 525 720 13 885 795 860 14 870 840 1 080 15 810 840 1 020 16 420 555 800 17 180 255 360 18 130 140 160 19 390 400 360 20 490 490 510 21 520 580 530 22 470 530 490 23 280 340 380 24 100 160 170 文章所提的调度控制策略是在一天内实时进行优化的，优化过程从某日0:00开始，到24:00结束，每小时为一个时段共计24个时段。由于光伏出力的不可控性及可能出现的随机因素，通过加入随机数来模拟优化过程中的不确定因素。由于此调度模型包含二次规划和二阶锥规划问题，故需利用Matlab编程求解。仿真所得有功及无功充放电功率如图4（a）及图4（b）所示，所得有功为校正后实际有功充放电功率。
图 4 优化结果
Figure 4. Optimization result
根据图4及图5可知，在充电站接入电网后，系统节点电压较为稳定，负荷峰谷差明显减小，降低系统网损，改善系统电压水平，增强了电力系统的稳定性，有利于实现功率的合理分配和能源的有效利用。
图 5 系统各时段等效负荷
Figure 5. Equivalent load of each time period in the system
-
在得到上层有功和无功功率的调度指令后，接下来就应该根据上层的调度指令控制下层V2G变换器。为了保证上层调度策略的实施，必须找到一种可用于能量双向传输的变换器及控制策略以保证功率的流通。文章搭建了改进VIENNA电路模型并利用改进VSG控制策略对其进行控制，最后利用以上IEEE33节点系统中26号变电站的数据进行仿真，说明了提出的变换器及控制策略的有效性。
-
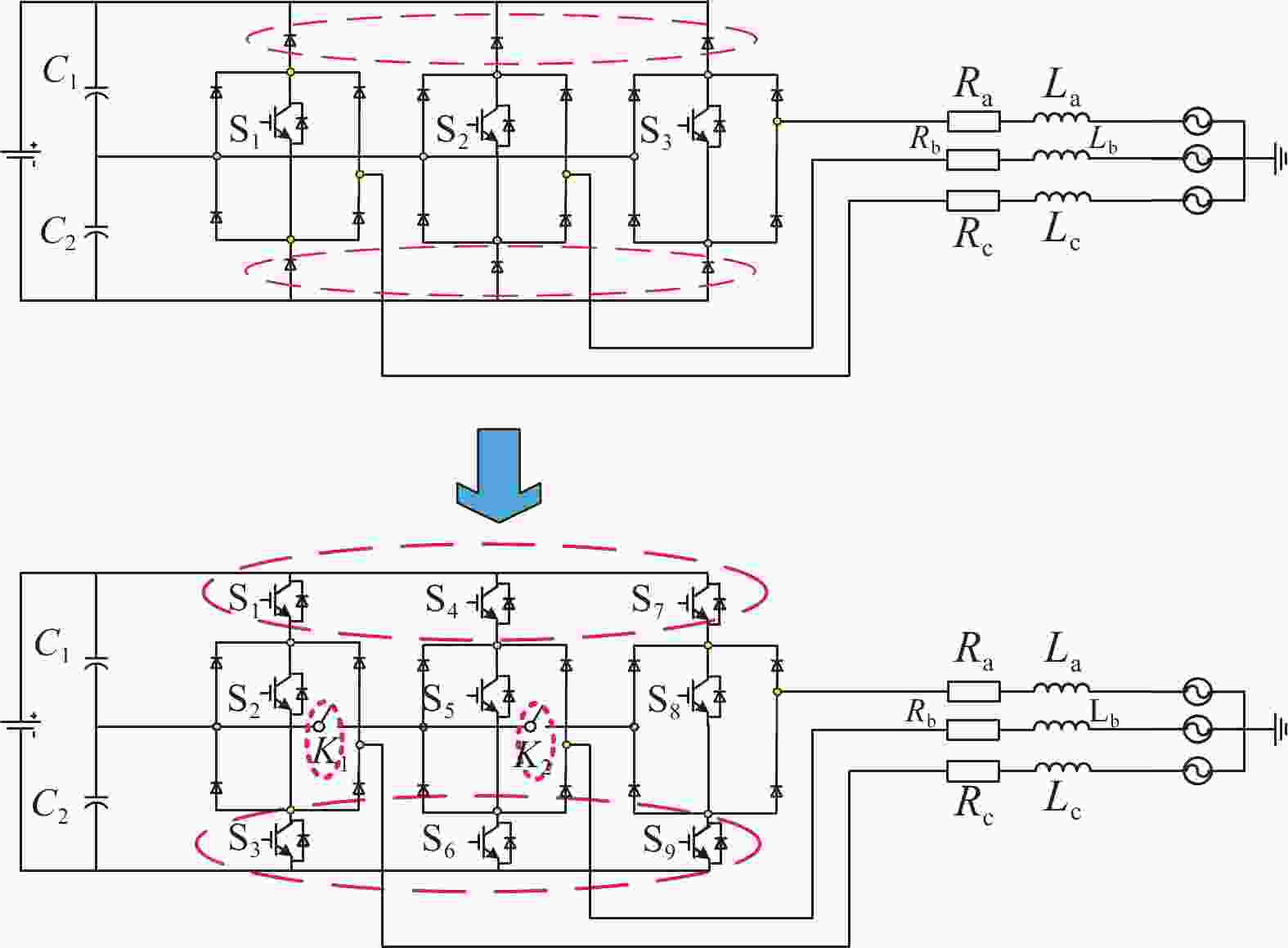
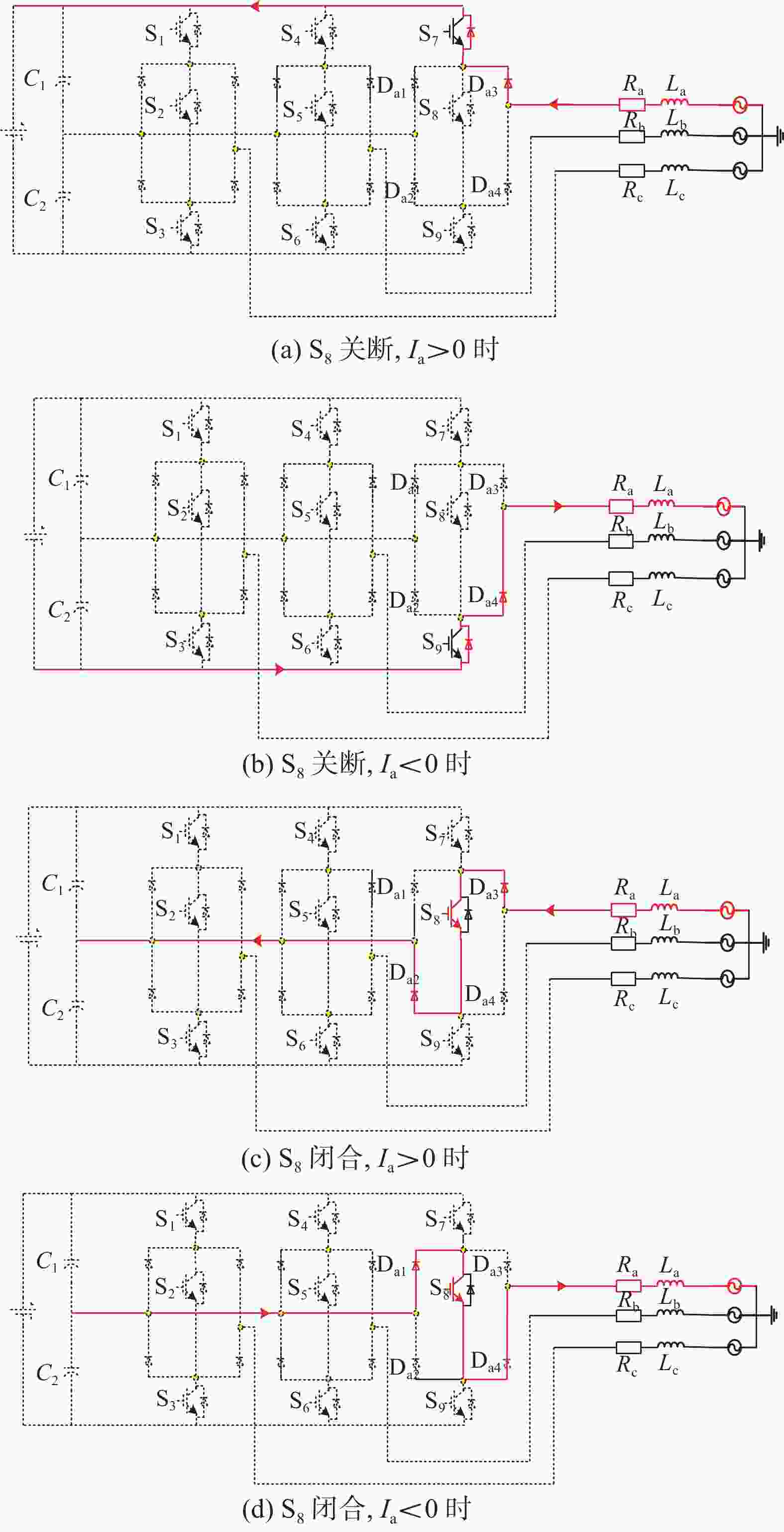
文章对传统VIENNA电路拓扑进行改进，将三个桥臂上的二极管改为开关管得到双向VIENNA电路（电路拓扑如图6所示）并利用改进VSG控制策略对其进行控制，其有充电与放电两种工作状态，充电时工作状态如图7所示：当开关S8关断时，Ia＞0则电流经Da3、S7流向负载，如图7（a）所示；Ia＜0则电流经S9、Da4流向电网，如图7（b）所示。当开关S8开通时，Ia＞0则电流经Da3、S8、Da2流向负载，如图7（c）所示；Ia＜0则电流经Da1、S8、Da4流向电网，如图7（d）所示。当处于充电状态时，由于并联二极管的存在，整体工作过程与传统VIENNA电路相同。
图 6 双向VIENNA电路
Figure 6. Bidirectional VIENNA circuit
图 7 双向VIENNA电路充电时电流流向
Figure 7. Current flow direction during bidirectional VIENNA circuit charging
-
VSG基本控制策略即模拟电力系统中同步电机的输出特性，使得电力电子变换器具有跟同步电机相同的阻尼特性与转动惯量，从而达到理顺电动汽车充电桩馈电与电网的关系，提高系统稳定性。由于VSG是通过类比同步发电机的输出特性得到的，故应先对同步发电机的特性进行分析。
在同步发电机中，分别通过控制转速和励磁调节系统实现有功及无功功率的输出调节。因此，同步发电机中最主要的方程有以下4个：
$$ {T_{\text{m}}} - {T_{\text{e}}} - {T_{\text{d}}} = J\frac{{\text{d}\omega }}{{\text{d}t}} $$ (15) $$ {P_m} = {P_{{\text{ref}}}} + {K_{\text{p}}}{\text{(}}\omega {\text{ - }}{\omega _{\text{0}}}{\text{)}} $$ (16) $$ Q{{ - }}{Q_{{\text{ref}}}}{\text{ = n(}}{U_n}{{ - }}U{\text{)}} $$ (17) $$ {R_{\text{s}}}I + {L_{\text{s}}}\frac{{\text{d}I}}{{\text{d}t}} + U = E $$ (18) 式中：
Tm −机械转矩（N·m）；
Te −电磁转矩（N·m）；
Td −阻尼转矩（N·m）；
Pm −机械功率（W）；
Pref −参考有功功率（W）；
Kp −有功−功率下垂系数；
Qref −参考无功（Var）；
n ——无功-电压下垂系数；
Un −给定参考电压（V）。
式（15）－式（17）分别为同步发电机的转子运动方程、调频方程及励磁调节方程。
可对上述方程进行推导类比，得到基本的虚拟同步发电机基本结构及控制框图如图8所示。
图 8 虚拟同步发电机
Figure 8. Virtual synchronous generator
以上虚拟同步发电机的基本控制思路为：通过机械功率Pe与角速度ω的比实现对机械转矩Tm的模拟，利用电磁功率Pe与ω之比模拟出电磁转矩Te，然后结合式（1）实现对有功功率的控制。经上述步骤得到ω之后，对其进行积分即可得到VSG机端电压相角θ，然后添加一个mode函数使得θ处于[0, 2π]范围内。无功控制部分采用电压-无功控制方法得到VSG的电压幅值E，然后根据式（4）模拟出电流，从而得到换流变压器的电压电流给定，通过与实际值进行比较得到PWM控制信号。
-
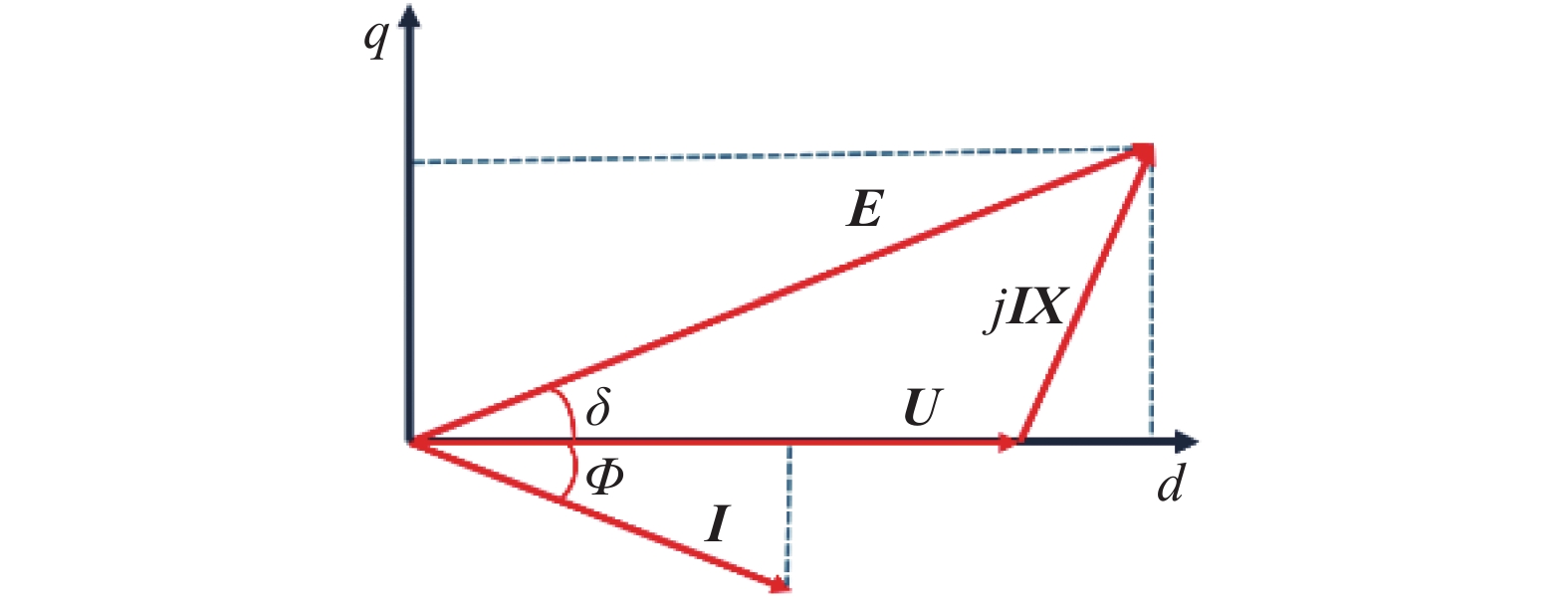
在VSG控制中，变换器交流侧电压与同步发电机类似，其电流电压矢量图如图9所示。
图 9 变换器交流侧矢量关系图
Figure 9. Vector relationship diagram on the AC side of the converter
其中E为输出电压，U为电网电压，I为变换器电流，X为变换器阻抗，δ为模拟功角，$\varPhi $为模拟阻抗角，由于线路中X >> R，故有E = U + jXI。在实际工作中，E以ω的角速度旋转，U以ω*的角速度旋转，当系统稳定时二者相等。
为了便于分析与仿真，对矢量进行dq分解可得：
$$ {\boldsymbol{I}}_{{\mathrm{q}}}=\frac{{\boldsymbol{E}} \cos \delta-{\boldsymbol{U}}}{{\boldsymbol{X}}} $$ (19) $$ {\boldsymbol{I}}_{{d}}=\frac{{\boldsymbol{E}} \sin \delta}{{\boldsymbol{X}}} $$ (20) 由于一般而言电感的电感上的压降很小，即jXI可近似为0，故有E≈U，sinδ≈δ，cosδ≈1，且X=ωL则可将上式近似为：
$$ {\boldsymbol{I}}_{q}=\frac{{\boldsymbol{E}}-{\boldsymbol{U}}}{\omega L} $$ (21) $$ {\boldsymbol{I}}_{d}=\frac{{\boldsymbol{E}} \delta}{\omega L} $$ (22) 由于E与U为旋转矢量，则二者之间的夹角可以表示为：
$$ \delta=\int\left(\omega-\omega^{*}\right) \text{d} t $$ (23) 联立式（22）－式（23）并进行拉氏变换，将E/ωL定义为常数K，则可得到式（24）。
$$ I_{{d}}={{K}} \frac{\omega-\omega^{*}}{S} $$ (24) 为提高系统的稳定性，用比例积分环节代替积分环节，则有：
$$ I_{{d}}^{*}={{K}}\left(1+\frac{1}{TS}\right)\left(\omega-\omega^{*}\right) $$ (25) 式（14）与发电机转子运动方程结合可将Id与有功给定建立联系。
由式（22）可知，Iq与变换器的输出电压U有关，则可利用无功-电压下垂控制来控制参考输出电压，再通过比例积分环节得到Iq给定。同时，为了使得无功输出具有一定的惯性且与Iq联系起来，可在Iq给定与无功控制中分别增加一个积分环节，则可得到：
$$ I_{q}^+={K}_{1}(E-U)+{K}_{2}\left(Q_{{\mathrm{ref}}}-Q\right) $$ (26) 由于电动汽车充电功率是恒定值，而V2G系统中由于电动汽车与电网连接，故系统不会处于孤岛模式，可以由电网向变换器实时提供频率与电压支持，故可对传统VSG控制进行改进得到V2G模式下的VSG控制策略，其控制框图如图10所示。
图 10 基于V2G模式的VSG控制策略框图
Figure 10. Block diagram of VSG control strategy based on V2G mode
-
为了验证上文所述的基于V2G模式的VIENNA双向变换电路及VSG控制策略的有效性，在Psim中搭建了改进型的VIENNA双向变换电路，整流时采用PWM控制，馈电时采用上文所述的基于V2G模式的VSG控制。电路参数设置如表2所示。
表 2 仿真参数设置
Table 2. Simulation parameter settings
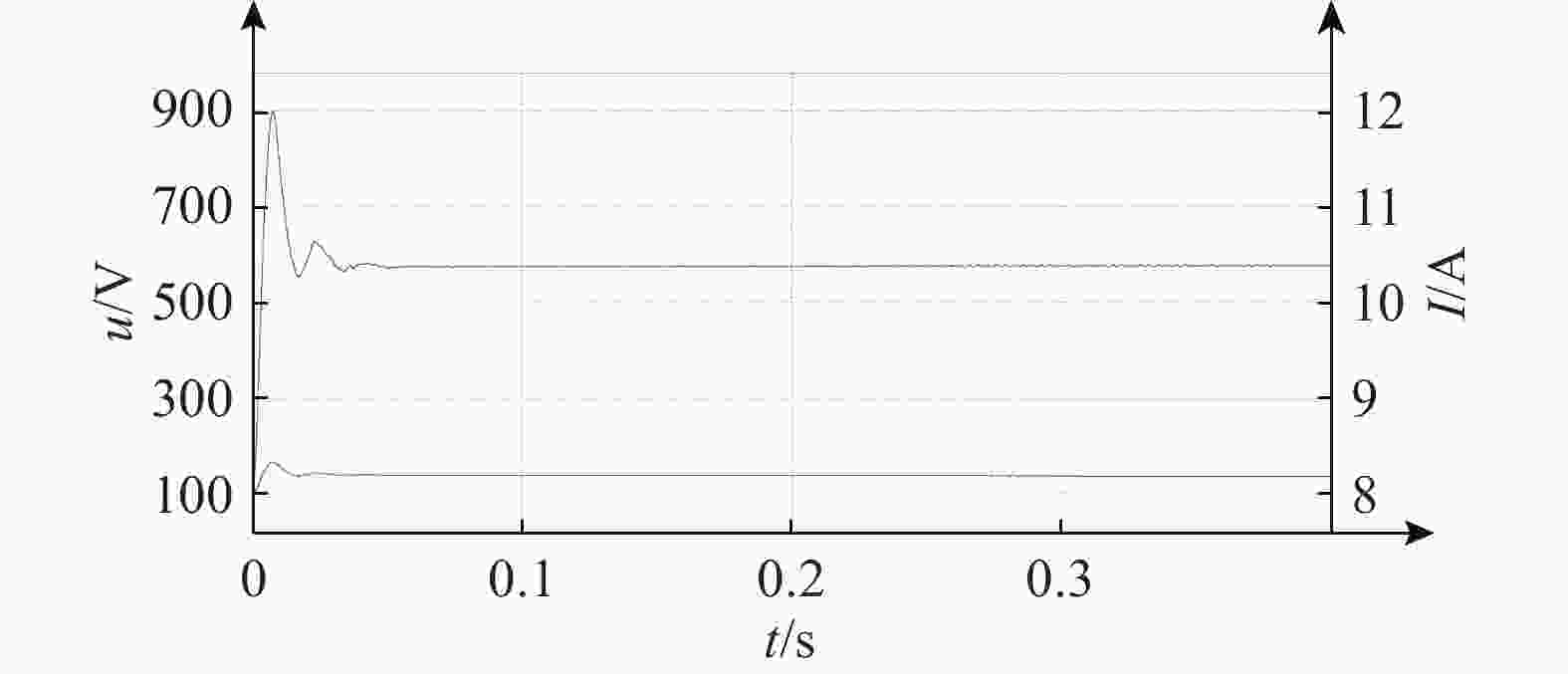
参数 数值 直流侧电池UDC/V 600 直流侧电容C/mF 2 交流侧电阻R/Ω 0.01 网侧电压有效值/V 380 交流侧电感L/mH 3 开关频率f/kHz 10 在整流模式下，由于工作方式同传统VIENNA电路拓扑相同，故不作重点分析，其直流侧输出电压波形及输出电流如图11所示。
图 11 整流模式电压电流波形
Figure 11. Rectification mode voltage and current waveform
可见当该拓扑工作于整流状态时，保留了传统VIENNA电路的优势，输出电流稳定，电流失真低，可保证电动汽车充电时能够良好工作。
当该拓扑工作于逆变状态时，即当电路工作于电动汽车电池向网侧输电的馈电状态时，设置其有功给定为5 kW，无功给定为0，所得交流侧电流电压波形如图12所示。
图 12 馈电状态网侧电压电流波形图
Figure 12. Voltage and current waveform diagram of the grid side in the feeding state
可见该拓扑输出到网侧的电压电流波形较好，能够输出较为稳定的有功及无功功率，可以完成V2G双向能量传播。
-
系统仿真参数与上文仿真参数一致。根据双层滚动优化调度策略所得结果，如图4（a）所示，即上层调度得到的有功和无功功率作为已知量提供给下层V2G变换器。设节点26充电站共有70个充电桩，根据时段14其有功输出为350 kW，无功输出为70 kvar，则平均每个充电桩有功输出为5 kW，无功输出为1 kvar。为了检验文中所提及的VSG调度控制方式的有效性，分别采用上文所述控制方式与PQ控制方式对双向VIENNA电路进行控制，为了体现控制方式效果差异，假设在t=0.2 s时调度指令发生了变化，有功功率给定从5 kW增加到6 kW，无功功率给定从1 kvar增加到2 kvar，在t=0.3 s时调度指令变回原值，即有功功率和无功功率变回至5 kW和1 kvar，对比电路功率输出结果如图13所示。
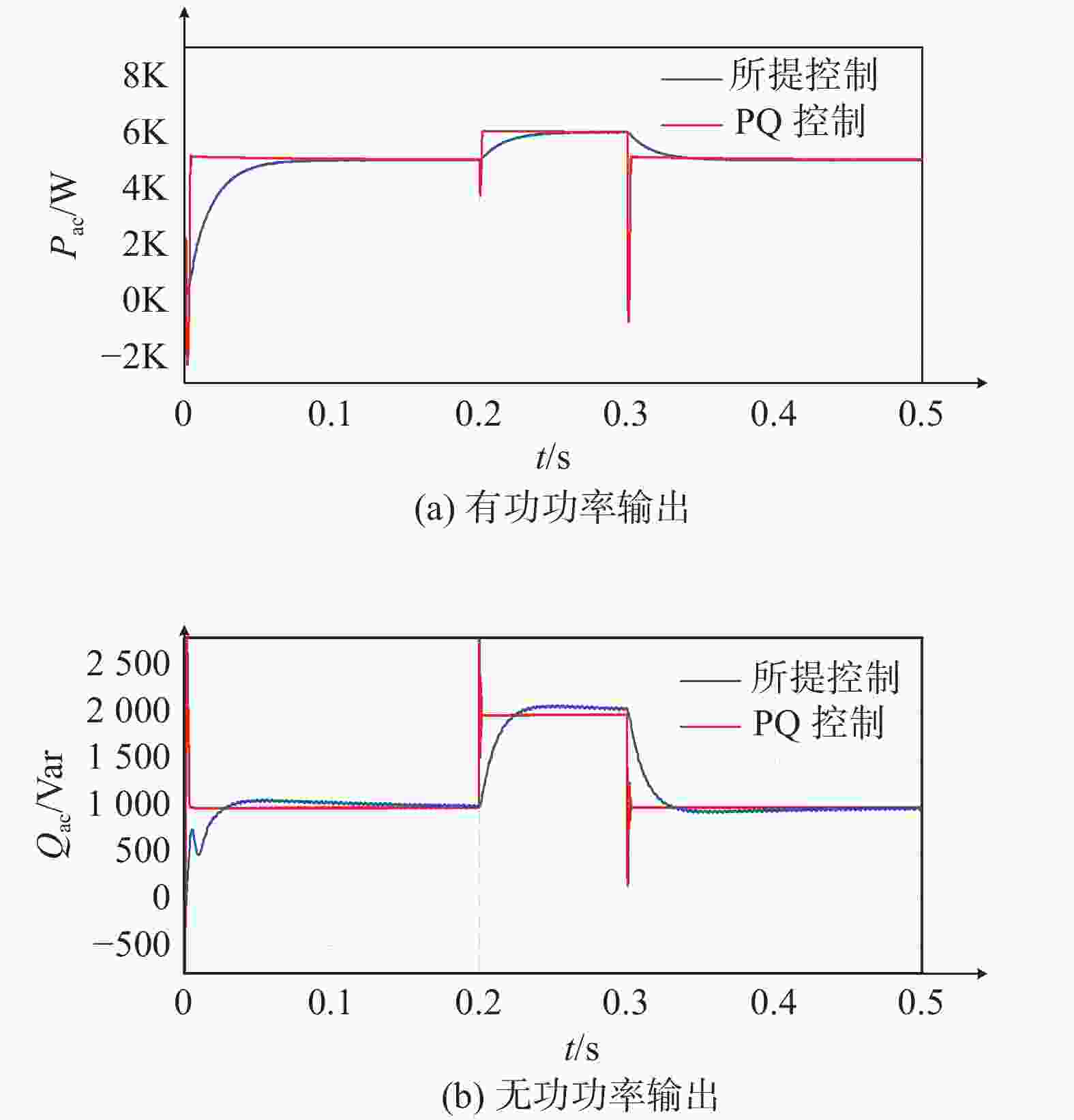
图 13 不同控制方式有功及无功功率变化
Figure 13. Changes in active and reactive power under different control methods
由图13可知，充电站充电桩采用PQ控制与改进VSG控制均可实现功率的调节，完成调度中心发布的充放电计划。但相较之下，PQ控制出现在功率变换的瞬间出现了严重的波动，而改进VSG控制使得变换器具有了类似于同步发电机的惯性特性，实现了功率的平缓过度，减少了对系统和电动汽车产生冲击，可配合上层调度策略建立性能较优的VSG系统。
-
文章针对新型V2G系统调度策略与充电站功率变换器的控制策略割裂的问题提出了一种面向新型电力系统将无功响应考虑在内的虚拟同步技术控制调度策略，通过仿真分析得到以下结论：
1）通过日前申请机制及负荷预测曲线制定分时电价引导用户错峰充放电，同时利用双层滚动优化模型进行实施优化，制定了负荷峰谷差小、电压水平好的最优调度计划并运用于IEEE33节点系统，结果表明以上调度计划提高了系统运行的稳定性。
2）为确保调度计划的实施，对充电站功率变换器开展了研究，以VIENNA电路为基础建立了双向功率变换器拓扑。结合V2G系统非孤岛工作模式及可由电网提供电压与频率支撑的运行特点对常规虚拟同步控制进行了简化与恒功率并网改进并利用改进后的虚拟同步控制方式对V2G双向功率变换器进行控制，在仿真验证中，上层要求分别增加输出有功和无功功率1 kW和1 kvar，并在0.1 s后恢复原有输出功率，相较于传统PQ控制，文章所提的控制在输出曲线中没有尖顶波，更加平滑。经仿真验证改进虚拟同步控制策略可跟踪滚动优化调度模型功率的变化，实现功率双向流动且可提供无功功率支撑，减小功率变换对V2G系统的冲击，提高系统稳定性。
将文章仿真结果与当前主流论文进行了对比，例如与文献[27]相对比，可以得出经过上层调度与下层变换器控制策略的配合，能够达到电网稳定性所要求水平。
由于数据原因，文章所用系统较小且建立在日前申请机制基础之上，只考虑提前预约电动汽车能源储备，对于未预约车辆不能对其能源进行优化与调度从而实现其充分利用。另一方面，文章调度策略及变换器控制策略未考虑每一辆电动汽车自身的约束，可能会因此导致整体调度计划无法充分实施，后续可探究如何将此约束考虑在内并简化优化过程并提高准确性。
V2G Scheduling Control Strategy Based on Virtual Synchronization
-
摘要:
目的 随着电动汽车数量的快速增加，电动汽车储能对电网的影响日益显著。为了实现电动汽车充电站与电网的动态交互，利用电动汽车储能调节负荷，以减小峰谷差和对电网的冲击，文章提出了一种基于虚拟同步技术的控制调度策略，考虑将无功响应纳入新型电力系统。 方法 首先，文章采用日前申请机制，建立了双层滚动优化调度模型，用于制定各充电站的充电计划。随后，针对V2G（Vehicle to Grid）系统的工作模式和特点，提出了一种改进型虚拟同步控制方式。该控制方式下，功率能够双向流动，并通过V2G调度控制策略进行最优分配，从而实现有功和无功的调度响应。 结果 实验结果表明：所提出的策略能够有效减小电动汽车充放电对电力系统的冲击，增强系统的稳定性。此外，通过将上层调度指令下发到下层V2G变换器控制上，可以很好地实现充电站与电网的双向互动。 结论 上层调度策略与下层变换器控制策略的结合，不仅满足了V2G系统的基本需求，还展现出良好的输出特性。这一控制调度策略为未来电力系统的稳定运行提供了有力保障。 Abstract:Objective With the rapid increase in the number of electric vehicles (EVs), the impact of EV energy storage on the power grid has become increasingly significant. To enable dynamic interaction between EV charging stations and the grid, and to use EV energy storage to regulate load in order to reduce peak-valley differences and mitigate grid impacts, this paper proposes a control and scheduling strategy based on virtual synchronous technology, considering the integration of reactive power response into the new power system. Method Firstly, a day-ahead application mechanism was adopted, and a two-layer rolling optimization scheduling model was established to formulate charging plans for each charging station. Then, considering the working mode and characteristics of the V2G (Vehicle to Grid) system, an improved virtual synchronous control method was proposed. Under this control method, power can flow bidirectionally, and optimal power distribution was achieved through the V2G scheduling control strategy, thereby realizing both active and reactive power dispatch responses. Result Experimental results show that the proposed strategy effectively reduces the impact of EV charging and discharging on the power system, enhancing system stability. Additionally, by issuing upper-level scheduling instructions to the lower-level V2G converter controls, bidirectional interaction between charging stations and the grid can be well realized. Conclusion The combination of the upper-level scheduling strategy and lower-level converter control strategy not only meets the basic needs of the V2G system but also demonstrates excellent output characteristics. This control and scheduling strategy provides strong support for the stable operation of future power systems. -
图 3 某日光伏、负荷功率预测曲线
Fig. 3 Photovoltaic and load power prediction curve for a certain day
图 7 双向VIENNA电路充电时电流流向
Fig. 7 Current flow direction during bidirectional VIENNA circuit charging
图 10 基于V2G模式的VSG控制策略框图
Fig. 10 Block diagram of VSG control strategy based on V2G mode
图 12 馈电状态网侧电压电流波形图
Fig. 12 Voltage and current waveform diagram of the grid side in the feeding state
图 13 不同控制方式有功及无功功率变化
Fig. 13 Changes in active and reactive power under different control methods
表 1 各充电站预约信息
Tab. 1. Appointment information for each charging station
时段 各充电站时段容量限制/kW 节点15充电站 节点23充电站 节点26充电站 1 155 190 165 2 185 165 170 3 185 190 225 4 190 200 225 5 255 350 195 6 335 455 355 7 310 295 300 8 425 455 395 9 525 515 495 10 335 295 285 11 255 195 280 12 735 525 720 13 885 795 860 14 870 840 1 080 15 810 840 1 020 16 420 555 800 17 180 255 360 18 130 140 160 19 390 400 360 20 490 490 510 21 520 580 530 22 470 530 490 23 280 340 380 24 100 160 170 
下载: 导出CSV
表 2 仿真参数设置
Tab. 2. Simulation parameter settings
参数 数值 直流侧电池UDC/V 600 直流侧电容C/mF 2 交流侧电阻R/Ω 0.01 网侧电压有效值/V 380 交流侧电感L/mH 3 开关频率f/kHz 10
下载: 导出CSV
-
[1] 黄珍瑶, 程诺, 江岳文. 考虑EV调峰需求响应可靠性的V2G聚合商多时间尺度调度策略 [J/OL]. 高电压技术, 2024: 1-11. (2024-04-16) [2024-07-17]. https://doi.org/10.13336/j.1003-6520.hve.20231247. HUANG Z Y, CHENG N, JIANG Y W. Multi-time-scale scheduling strategy of V2G aggregators considering EV peak regulating demand response reliability [J/OL]. High voltage engineering, 2024: 1-11.(2024-04-16) [2024-07-17]. https://doi.org/10.13336/j.1003-6520.hve.20231247. [2] 王锡凡, 邵成成, 王秀丽, 等. 电动汽车充电负荷与调度控制策略综述 [J]. 中国电机工程学报, 2013, 33(1): 1-10. DOI: 10.13334/j.0258-8013.pcsee.2013.01.005. WANG X F, SHAO C C, WANG X L, et al. Survey of electric vehicle charging load and dispatch control strategies [J]. Proceedings of the CSEE, 2013, 33(1): 1-10. DOI: 10.13334/j.0258-8013.pcsee.2013.01.005. [3] 张灿, 张明震. 中国新型公路交通能源综合系统发展对策研究 [J]. 南方能源建设, 2024, 11(5): 95-104. DOI: 10.16516/j.ceec.2024.5.10. ZHANG C, ZHANG M Z. Countermeasures for the development of China's new highway transportation-energy integrated system [J]. Southern energy construction, 2024, 11(5): 95-104. DOI: 10.16516/j.ceec.2024.5.10. [4] 蔡黎, 高乐, 徐青山, 等. 电动汽车V2G关键技术研究及应用进展 [J]. 电池, 2020, 50(1): 87-89. DOI: 10.19535/j.1001-1579.2020.01.021. CAI L, GAO L, XU Q S, et al. Research and application progress in V2G key technology of electric vehicle [J]. Battery bimonthly, 2020, 50(1): 87-89. DOI: 10.19535/j.1001-1579.2020.01.021. [5] SHI Z H, RUAN J H, HONG Y Y, et al. Dual-module VSG control strategy under unbalanced voltage conditions [J]. Journal of power electronics, 2023, 23(6): 923-934. DOI: 10.1007/s43236-022-00587-8. [6] 裴振坤, 王学梅, 康龙云, 等. 考虑用户充电计划的电动汽车辅助调频控制策略 [J]. 电力工程技术, 2023, 42(1): 88-97. DOI: 10.12158/j.2096-3203.2023.01.011. PEI Z K, WANG X M, KANG L Y, et al. Auxiliary frequency regulation control strategy for electric vehicles considering users' charging plans [J]. Electric power engineering technology, 2023, 42(1): 88-97. DOI: 10.12158/j.2096-3203.2023.01.011. [7] HAN J G, ZHOU X, LU S, et al. A three-phase bidirectional grid-connected AC/DC converter for V2G applications [J]. Journal of control science and engineering, 2020, 2020: 8844073. DOI: 10.1155/2020/8844073. [8] 王军章, 兰征. 虚拟同步发电机用双向直流变换器研究 [J]. 浙江电力, 2019, 38(4): 20-27. DOI: 10.19585/j.zjdl.201904004. WANG J Z, LAN Z. Study on bidirectional DC/DC converter for virtual synchronous machine [J]. Zhejiang electric power, 2019, 38(4): 20-27. DOI: 10.19585/j.zjdl.201904004. [9] 赵昕辰. 基于虚拟同步机控制技术的电动汽车V2G系统研究 [D]. 济南: 山东大学, 2020. DOI: 10.27272/d.cnki.gshdu.2020.002543. ZHAO X C. Research on electric vehicle V2G system based on virtual synchronous machine control technology [D]. Jinan: Shandong University, 2020. DOI: 10.27272/d.cnki.gshdu.2020.002543. [10] PARAMASIVAM S K, RAMU S K, CHOLAMUTHU P. Unit vector template control strategy-based harmonic mitigation and charging with three phase-three level-three switch Vienna rectifier for level 3 electric vehicle charging applications [J]. International journal of circuit theory and applications, 2024, 52(6): 2889-2915. DOI: 10.1002/cta.3904. [11] 全生明, 苏舒, 赵楠, 等. 基于最优效率的双有源桥变换器参数设计优化方法 [J]. 电气工程学报, 2022, 17(2): 56-64. DOI: 10.11985/2022.02.007. QUAN S M, SU S, ZHAO N, et al. Design method of dual active bridge based on the optimum efficiency [J]. Journal of electrical engineering, 2022, 17(2): 56-64. DOI: 10.11985/2022.02.007. [12] 兰才华, 石荣亮, 王国斌, 等. 基于频率前馈补偿的储能VSG并网有功响应优化策略 [J]. 太阳能学报, 2024, 45(2): 236-243. DOI: 10.19912/j.0254-0096.tynxb.2022-1535. LAN C H, SHI R L, WANG G B, et al. Optimization strategy of grid-connected active power response of grid-connected active of energy storage VSG based on frequency feedforward compensation [J]. Acta energiae solaris sinica, 2024, 45(2): 236-243. DOI: 10.19912/j.0254-0096.tynxb.2022-1535. [13] ZHAO X C, WANG H, WANG K. Research on virtual synchronous generator control for vehicle-to-grid system [C]// Anon. Proceedings of 2019 4th Asia Conference on Power and Electrical Engineering, Hangzhou, China, March 28-31, 2019. Hangzhou: IOP, 2019: 56-64. DOI: 10.1088/1757-899X/486/1/012048. [14] 管敏渊, 姚瑛, 吴圳宾, 等. 基于RBF神经网络的储能VSG控制策略优化 [J]. 浙江电力, 2024, 43(3): 55-64. DOI: 10.19585/j.zjdl.202403007. GUAN M Y, YAO Y, WU Z B, et al. Optimization of energy storage VSG control strategy based on RBF neural networks [J]. Zhejiang electric power, 2024, 43(3): 55-64. DOI: 10.19585/j.zjdl.202403007. [15] 朱作滨, 孙树敏, 丁月明, 等. 基于VSG的低电压穿越控制策略研究 [J]. 太阳能学报, 2024, 45(2): 376-383. DOI: 10.19912/j.0254-0096.tynxb.2022-1661. ZHU Z B, SUN S M, DING Y M, et al. Study on low voltage ride through control strategy based on VSG [J]. Acta energiae solaris sinica, 2024, 45(2): 376-383. DOI: 10.19912/j.0254-0096.tynxb.2022-1661. [16] WU W H, CHEN Y D, ZHOU L M, et al. Sequence impedance modeling and stability comparative analysis of voltage-controlled VSGs and current-controlled VSGs [J]. IEEE transactions on industrial electronics, 2019, 66(8): 6460-6472. DOI: 10.1109/TIE.2018.2873523. [17] 程启明, 余德清, 程尹曼, 等. 基于自适应旋转惯量的虚拟同步发电机控制策略 [J]. 电力自动化设备, 2018, 38(12): 79-85. DOI: 10.16081/j.issn.1006-6047.2018.12.012. CHENG Q M, YU D Q, CHENG Y M, et al. Control strategy of virtual synchronous generator based on adaptive rotational inertia [J]. Electric power automation equipment, 2018, 38(12): 79-85. DOI: 10.16081/j.issn.1006-6047.2018.12.012. [18] 游磊, 金小明, 刘云. 电动汽车集群充电负荷计算方法研究 [J]. 南方能源建设, 2024, 11(5): 159-167. DOI: 10.16516/j.ceec.2024.5.17. YOU L, JIN X M, LIU Y. Research on the charging load calculation method for electric vehicle cluster [J]. Southern energy construction, 2024, 11(5): 159-167. DOI: 10.16516/j.ceec.2024.5.17. [19] 赵浩然. 可再生能源发电与电动汽车的协同调度策略研究 [D]. 济南: 山东大学, 2020. DOI: 10.27272/d.cnki.gshdu.2020.001215. ZHAO H R. Research on cooperative scheduling strategy of renewable energy and electric vehicles [D]. Jinan: Shandong University, 2020. DOI: 10.27272/d.cnki.gshdu.2020.001215. [20] 王冠, 刘苏贤, 赵浩然, 等. 考虑电动汽车充电桩无功响应的优化调度策略 [J]. 湖南大学学报(自然科学版), 2021, 48(10): 152-160. DOI: 10.16339/j.cnki.hdxbzkb.2021.10.018. WANG G, LIU S X, ZHAO H R, et al. Optimal dispatching strategy considering reactive response of electric vehicle charging piles [J]. Journal of Hunan University (Natural Sciences Edition), 2021, 48(10): 152-160. DOI: 10.16339/j.cnki.hdxbzkb.2021.10.018. [21] 赵玉, 徐天奇, 李琰, 等. 基于分时电价的电动汽车调度策略研究 [J]. 电力系统保护与控制, 2020, 48(11): 92-101. DOI: 10.19783/j.cnki.pspc.190770. ZHAO Y, XU T Q, LI Y, et al. Research on electric vehicle scheduling strategy based on time-shared electricity price [J]. Power system protection and control, 2020, 48(11): 92-101. DOI: 10.19783/j.cnki.pspc.190770. [22] 王晞, 汪伟, 王海燕, 等. 计及用户电池损耗的电动汽车分布式两阶段调度策略 [J]. 电测与仪表, 2022, 59(1): 120-126. DOI: 10.19753/j.issn1001-1390.2022.01.016. WANG X, WANG W, WANG H Y, et al. Distributed two-stage scheduling strategy of EV considering user battery consumption [J]. Electrical measurement & instrumentation, 2022, 59(1): 120-126. DOI: 10.19753/j.issn1001-1390.2022.01.016. [23] 戴越繁, 杨伟. 计及电池动态损耗的电动汽车分层调度策略 [J]. 电测与仪表, 2021, 58(7): 19-26. DOI: 10.19753/j.issn1001-1390.2021.07.003. DAI Y F, YANG W. A hierarchical optimal scheduling strategy for electric vehicles considering dynamic battery loss [J]. Electrical measurement & instrumentation, 2021, 58(7): 19-26. DOI: 10.19753/j.issn1001-1390.2021.07.003. [24] 陈海瑞, 米增强, 贾雨龙, 等. 计及电价不确定的电动汽车聚合商区间调度策略 [J]. 电测与仪表, 2021, 58(12): 24-30. DOI: 10.19753/j.issn1001-1390.2021.12.004. CHEN H R, MI Z Q, JIA Y L, et al. Interval scheduling strategy for electric vehicle aggregator considering uncertainty of electricity price [J]. Electrical measurement & instrumentation, 2021, 58(12): 24-30. DOI: 10.19753/j.issn1001-1390.2021.12.004. [25] 薄鑫, 韩笑, 许偲轩, 等. 基于指标排序的电动汽车聚合控制策略 [J]. 电测与仪表, 2019, 56(12): 135-139, 152. DOI: 10.19753/j.issn1001-1390.2019.012.022. BO X, HAN X, XU S X, et al. Research on the control strategy of electric vehicle polymerization based on the ranking of indicators [J]. Electrical measurement & instrumentation, 2019, 56(12): 135-139, 152. DOI: 10.19753/j.issn1001-1390.2019.012.022. [26] EHSANI M, FALAHI M, LOTFIFARD S. Vehicle to grid services: potential and applications [J]. Energies, 2012, 5(10): 4076-4090. DOI: 10.3390/en5104076. [27] 杨铎. 计及电动汽车电池集中充电站接入的电网稳定性分析 [D]. 北京: 华北电力大学, 2014. DOI: 10.7666/d.Y2658510. YANG D. Analysis of electric vehicle battery centralized charging station on power system stability [D]. Beijing: North China Electric Power University, 2014. DOI: 10.7666/d.Y2658510. -
图(13) / 表 (2)
计量
- 文章访问数: 283
- HTML全文浏览量: 153
- PDF下载量: 22
- 被引次数: 0
