-
风能长期以来已被证实是一种有效的传统能源替代品[1]。近二十年来，随着全球能源、环境及资源问题的日益凸显，特别是全球变暖和化石能源日益枯竭，大力发展可再生能源、加快能源体系绿色低碳转型的呼声越来越明显[2]。风能作为一种清洁能源，因其在减少温室气体排放和保障能源供应方面的显著优势，已经被全球众多国家广泛采纳，作为应对气候变化和增强能源安全的战略选择[3]。
风力发电机在运行过程中会产生尾流，尾流中的气流会对后续的风力发电机产生干扰[4-5]，导致性能下降，并对周围环境产生不利影响。为了减少这种干扰，提高风力发电机的运行效率，需要采取相应的尾流干扰抑制策略。
瑞典航空研究院是最早通过风洞试验来探究风力发电机尾流路径的研究机构之一[6]。Vermeulen等[7-8]利用风洞试验，对风力发电机组的尾流现象进行了深入研究，分析了包括湍流强度等多种影响因素。Krogstad等在挪威科技大学的风洞实验室进行了一系列的实验研究，深入研究了单风机气动特性以及两风机风电场复杂尾流特性[9-10]。挪威学者在风洞实验室深入探讨了单个风力发电机的空气动力学特性以及双机风电场中的复杂尾流行为[11-12]。郭静婷[13]利用风电场的实际测量数据，探究在主要风向条件下风力发电机之间的相互影响，并且还研究了优化风电场的布局。Whale等[14]利用PIV（Partic Leimage Velocimetry）技术来捕捉风机风轮旋转产生的尾涡结构，进而研究风机的尾流特性。Nowitech和Norcowe对串列式两风力发电机进行了盲测实验，对多台风力发电机尾流干扰现象采用不同的数值模拟进行了对比分析。郭茂丰等[15]分析了不同偏航角度下风力发电机尾迹中心的偏移情况和尾迹区域的湍流强度变化，风力发电机尾迹的上侧和下侧湍流强度分布呈现出不对称性，这种不对称性导致湍流强度的变化也不相同，使得风力发电机尾迹的湍流环境变得更加复杂。Fletcher等[16]采用基于CFD（Computational Fluid Dynamics）方法的涡传递模型研究了两风力发电机场中的尾流相互干扰现象，探讨了在不同条件下，下游风力发电机位于上游风力发电机全尾流区域或部分尾流区域时的尾流干扰效应。
文章采用国家可再生能源实验室NREL-5 MW风力发电机模型，使用Star-ccm+软件对串列双风力发电机尾流干扰效应抑制策略进行了研究。采用对上游风力发电机不同偏航角，上游风力发电机与下游风力发电机之间的塔架高差及横向间距3种情况在单一及两两组合下的不同控制策略，通过合理调整这些参数，可以有效减少风力发电机之间的尾流干扰。
-
风力发电机在正常工作时，风速一般处于5～25 m/s的范围之内，在此风速范围内，可以假设风电场的流场为不可压缩流场。因此，通过求解不可压缩Navier-stokes（N-S）方程来进行对风电场尾流相互影响的数值模拟研究，其基本控制方程如下：
$$ \frac{\partial }{{\partial {{{x}}_{{i}}}}}\left( {{{{u}}_{{i}}}} \right) = 0 $$ (1) $$ \rho \frac{\partial }{{\partial {{t}}}}\left( {{{{u}}_{{i}}}} \right) + \frac{\partial }{{\partial {{{x}}_{{j}}}}}\left( {\rho {u_i}{u_j} + p{\delta _{ij}} - {\tau _{ij}}} \right) = \rho {{f'}_i} $$ (2) 式中：
ρ ——空气密度（kg/m3）；
ui、uj ——i和j方向速度分量（m/s）；
p ——压力（Pa）；
fi′ ——体力单位质量（N/kg）；
$ \delta $ij ——克罗内克符号；
$ \tau $ij ——作用于流体粒子的应力（N/m2）。
-
SST k-ω湍流模型是一种两方程雷诺平均模型，结合k-ω模型和k-ε模型的特点对在近壁区域和自由剪切流区域流动进行准确预测。该方程表达如下：
$$ \frac{\partial}{\partial t}(\rho k)+\frac{\partial}{\partial x_i}\left(\rho k u_i\right)= \frac{\partial}{\partial x_i}\left(\varGamma_k \frac{\partial k}{\partial x_j}\right)+G_{\mathrm{k}}-Y_{\mathrm{k}}+S_{\mathrm{k}} $$ (3) $$ \frac{\partial }{{\partial {{t}}}}\left( {\rho {\omega}} \right) + \frac{\partial }{{\partial {{{x}}_{{i}}}}}\left( {\rho {\omega}{{{u}}_{{i}}}} \right) = \frac{\partial }{{\partial {{{x}}_{{i}}}}}\left( {{\varGamma _{\omega}}\frac{{\partial {\omega}}}{{\partial {{{x}}_{{j}}}}}} \right) + {G_{\text{ω}}} - {Y_{\text{ω}}} + {D_{\text{ω}}} + {S_{\text{ω}}} $$ (4) 式中：
k ——湍动能（J/m³）；
$ \omega $ ——比耗散率；
$ \varGamma $k ——含有k的有效扩散项；
$ \varGamma_{\text{ω}} $ ——含有$ \omega $的有效扩散项；
Yk ——湍动能的耗散项；
$ Y_\text{ω} $ ——耗散率的耗散项；
Gk ——湍动能的生成项；
$ G_\text{ω} $ ——耗散率的生成项；
$ D_\text{ω} $ ——正交发散项；
Sk、$ S_\text{ω} $ ——自定义项。
-
控制流体流动问题的方程是连续性（质量守恒）、纳维-斯托克斯（动量守恒）和能量方程。计算流体动力学是一种用一组代数方程（该过程称为离散化）代替控制流体流动的微分方程的技术，而这又可以借助数字计算机来求解，从而获得近似解。
以有限体积法（FVM）为例，其核心步骤如下：
（1）域的划分：首先将研究区域划分为许多小的控制体积，每个控制体积的中心点是关注的变量所在位置；
（2）控制方程的积分：在每个控制体积上，将控制方程的微分形式进行积分，这一过程与控制体积方法类似；
（3）变量插值：在控制体积的边界上，通过插值方法来描述变量在网格节点之间的变化情况；
（4）守恒原理的应用：通过这种方式得到的离散方程确保了控制体积内变量的守恒性。
-
本节采用NREL-5 MW单风力发电机[17]的气动性能进行网格无关性验证，通过增加单元总数，同时监测上游转子的推力，来验证了网格的独立性。为了平衡计算费用和精度，网格单元总数为
2000 万，其中每个转子区域有1200 万个网格单元。此外，为了确保上游风力发电机的尾流有足够的时间发展，计算模拟的时间设定为上游风力发电机完整旋转40个周期的时间，即200 s。同时，本文的时间步长选为转子旋转5°所需的时间，即0.06887 s，满足精确性的要求[18]。在风力发电机数值模拟中，确保风力发电机旋转区域的网格划分精准是至关重要的，故对风力发电机旋转区域网格选取了3种不同尺寸的旋转区域网格的计算结果来排除网格差异的影响，分别为Mesh1、Mesh2、Mesh3，网格旋转域的数量由疏至密，如表1所示。在3种网格中，Mesh2和Mesh3 2种网格的推力相当，功率也仅差0.4%。在综合考虑计算成本情况下，采用Mesh2的效果会更好。此时风力发电机气动功率的输出稳定在5.26 MW左右，本文采用的NREL-5 MW风力发电机的额定功率为5.3 MW左右，误差在可接受范围内。风力发电机的功率输出由转子的顺时针转矩估算，如式（5）所示。
表 1 3种不同网格下的风力发电机推力和功率数值
Table 1. Values of wind turbine thrust and power for three different grids
网格 网格
总数/万流体域
网格/万旋转区域
网格/万推力/kN 功率/MW Mesh1 1580 780 800 707
(0.6%)5.22
(1.1%)Mesh2 2000 780 1220 711
(0.0%)5.26
(0.4%)Mesh3 2 590 780 1810 711
(0.0%)5.28
(0.3%)$$ P = \frac{{2\text{π} n}}{{60}} \cdot M $$ (5) 式中：
P ——输出功率（MW）；
M ——转子的转矩（N/m）；
n ——转子转速（rpm）。
-
对切入风速3 m/s到额定风速11.4 m/s进行了多次稳态模拟，以测试验证结果。表2提供了本文计算的上游风力发电机功率的结果与其他文献结果的比较。结果表明，本文结果与文献[19-22]的研究结果吻合较好，且相应的误差均在可接受的范围内。
-
表3为下游风力发电机功率的对比。本文下游风力发电机功率计算结果与文献[22-24]有些差别，主要原因可能是双风力发电机间距不同造成的。本文的下游风力发电机在5D（D为风力发电机直径）近尾流位置处的入流风速显著降低，导致下游风力发电机输出功率较小；而文献中下游风力发电机位于7D远尾流区域，入流速度已得到恢复，使得下游风力发电机输出功率出现差异。
-
上下游风力发电机之间的间隔距离定义为Δx，上游风力发电机与出口位置的距离设置为15D−Δx。计算区域的长度沿着风向为19D，横向宽度为4D，高度为3.2D。上游风力发电机相对于入流方向的夹角设定为θ，下游风力发电机与上游风力发电机的塔架高差设置为ΔH，下游风力发电机沿+y方向偏移的距离设置为Δy。
如图1所示为串列双风力发电机在偏航角、塔架高差及横向间距3种不同工况下布置图。
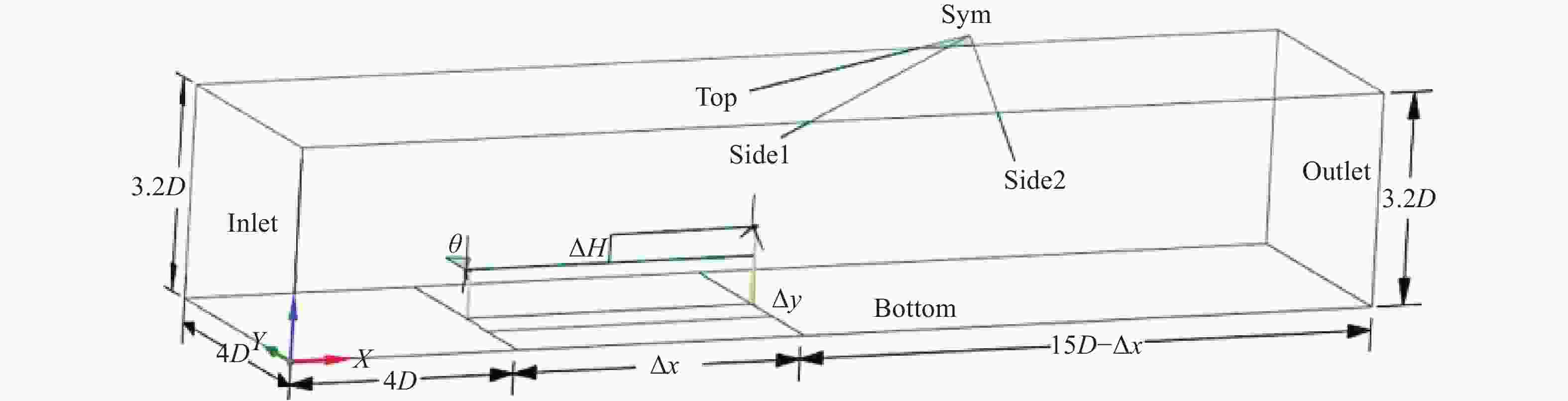
图 1 串列布置双风力发电机计算模型示意图
Figure 1. Schematic diagram of the computational model for tandem-arranged dual wind turbines
在设定边界条件时，入口边界被定义为具有恒定特性的自由流，其中指定的来流风速设定为11.4 m/s，且风向与风力发电机塔架的连线保持一致。2台风力发电机均按照其额定转速，即12.1 rpm进行运转。此外，其他参数均与验证算例一致。
工况方面，根据设定的不同风力发电机偏航角θ、塔架高差ΔH和横向间距Δy进行不同变量工况下算例的设置，见表4；根据设定的不同风力发电机偏航角θ、塔架高差ΔH和横向间距Δy进行两两组合进行算例的设置，见表5－表7。其中，H1与H2分别表示上/下游风力发电机塔架高度。
表 4 不同变量工况下算例参数设置
Table 4. Parameter settings for case studies under various variable cases
变量 工况 Δx θ/(°) Δy θ A1 5D 10 0 A2 20 0 A3 30 0 A4 40 0 Δy B1 5D 0 1/8D B2 0 2/8D B3 0 3/8D B4 0 4/8D B5 0 5/8D B6 0 6/8D 变量 工况 H1/m H2/m ΔH ΔH C1 90 184.5 −15/20D C2 90 165.6 −12/20D C3 90 146.7 −9/20D C4 90 127.8 −6/20D C5 90 108.9 −3/20D C0 90 90 0 C6 108.9 90 +3/20D C7 127.8 90 +6/20D C8 146.7 90 +9/20D C9 165.6 90 +12/20D C10 184.5 90 +15/20D 表 5 不同θ与ΔH工况组合时，算例参数设置
Table 5. Parameter settings at different θ and ΔH cases
算例编号 Δx θ/(°) ΔH 1 5D 10 −3/20D 2 5D 10 −6/20D 3 5D 10 −9/20D 4 5D 20 −3/20D 5 5D 20 −6/20D 6 5D 20 −9/20D 7 5D 30 −3/20D 8 5D 30 −6/20D 9 5D 30 −9/20D 10 5D 40 −3/20D 11 5D 40 −6/20D 12 5D 40 −9/20D 表 6 不同θ与Δy工况组合时，算例参数设置
Table 6. Parameter settings at different θ and Δy cases
算例编号 Δx θ/(°) Δy 1′ 5D 10 1/8D 2′ 5D 10 2/8D 3′ 5D 10 3/8D 4′ 5D 10 4/8D 5′ 5D 20 1/8D 6′ 5D 20 2/8D 7′ 5D 20 3/8D 8′ 5D 20 4/8D 9′ 5D 30 1/8D 10′ 5D 30 2/8D 11′ 5D 30 3/8D 12′ 5D 30 4/8D 13′ 5D 40 1/8D 14′ 5D 40 2/8D 15′ 5D 40 3/8D 16′ 5D 40 4/8D 表 7 不同ΔH与Δy工况组合时，算例参数设置
Table 7. Parameter settings at different ΔH and Δy cases
算例编号 Δx ΔH Δy 1′′ 5D −3/20D 1/8D 2′′ 5D −3/20D 2/8D 3′′ 5D −3/20D 3/8D 4′′ 5D −3/20D 4/8D 5′′ 5D −6/20D 1/8D 6′′ 5D −6/20D 2/8D 7′′ 5D −6/20D 3/8D 8′′ 5D −6/20D 4/8D 9′′ 5D −9/20D 1/8D 10′′ 5D −9/20D 2/8D 11′′ 5D −9/20D 3/8D 12′′ 5D −9/20D 4/8D -
本节主要研究在不同偏航角度条件下，下游风力发电机受到上游风力发电机尾流的影响。上游风力发电机的气动功率基本不变，对下游风力发电机功率的提升比定义为：
$$ R = \frac{{{{\bar P}_{i}} - {{\bar P}_{\text{1}}}}}{{{{\bar P}_{\text{1}}}}} \times 100\% $$ (6) 式中：
$ {\bar P_1} $——在上游风力发电机没有偏航角度的情况下，下游风力发电机的气动功率（MW）；
$ {\bar P_i} $——在考虑上游风力发电机不同偏航角度时，下游风力发电机的气动功率（MW）。
图2展示了在不同上游风力发电机偏航角工况下的上下游风力发电机及串列双风力发电机的平均气动功率及功率提升比。其中功率提升比表示的是风力发电机在不同偏航角工况下的气动功率输出和在偏航角为零的工况下的气动功率输出的比值。结果表明下游风力发电机以及串列双风力发电机的气动功率输出与上游风力发电机的偏航角有着密切的关系。
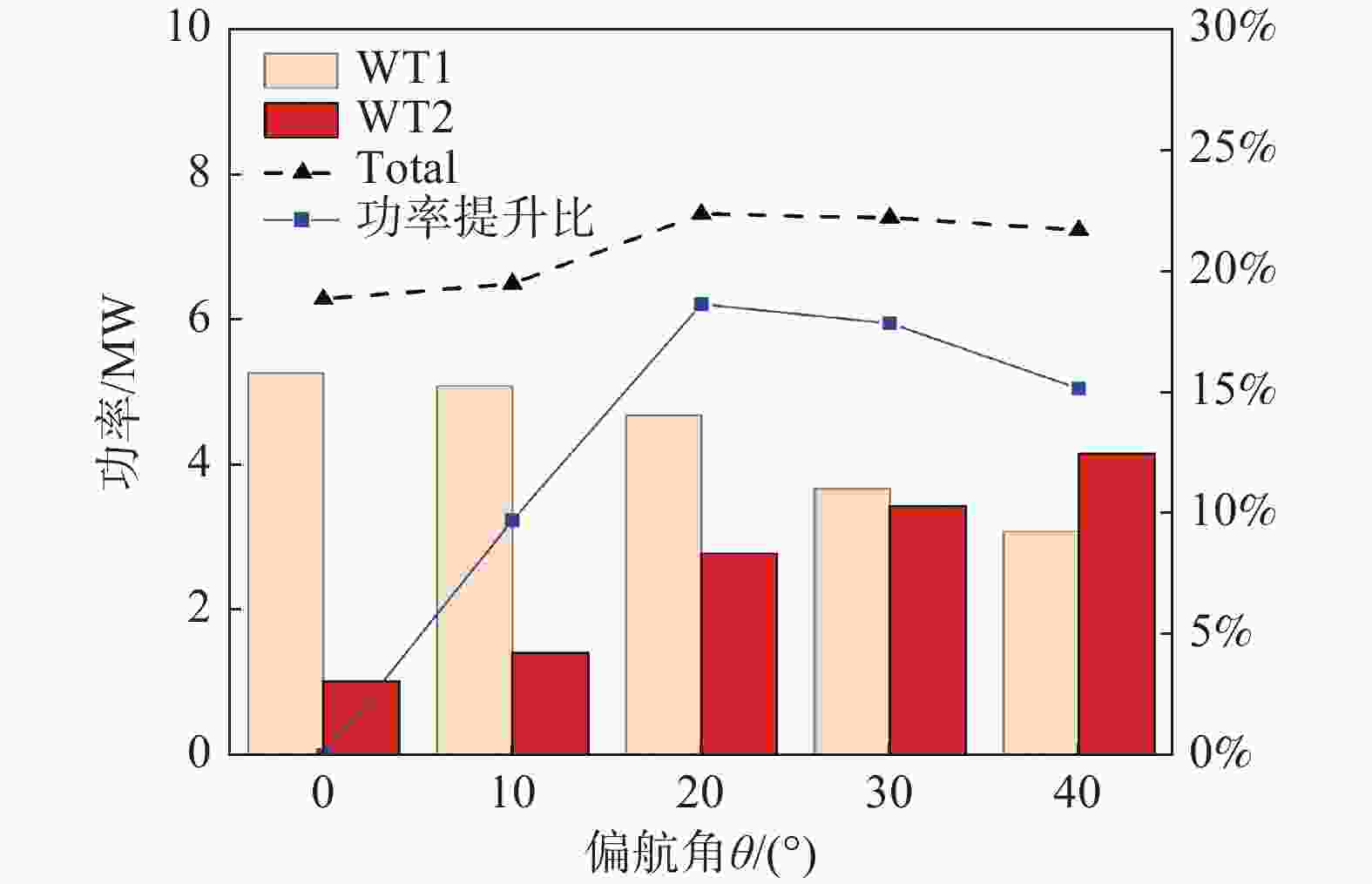
图 2 不同θ工况下双风力发电机平均气动功率及整体功率提升比
Figure 2. Average aerodynamic power and overall power gain ratio for dual wind turbines under various θ cases
为了阐明风力发电机功率随着偏航角变化的关系，对轮毂高度水平面上的平均尾流速度分布及流场涡量分布进行了深入分析，如图3所示。在平均尾流速度分布图中，横轴以风力发电机直径的2倍（2D）作为测量单位，平均速度曲线向左偏移表示风速降低，向右偏移则表示风速回升，降低的风速幅度可以通过偏移幅度的一半来确定。
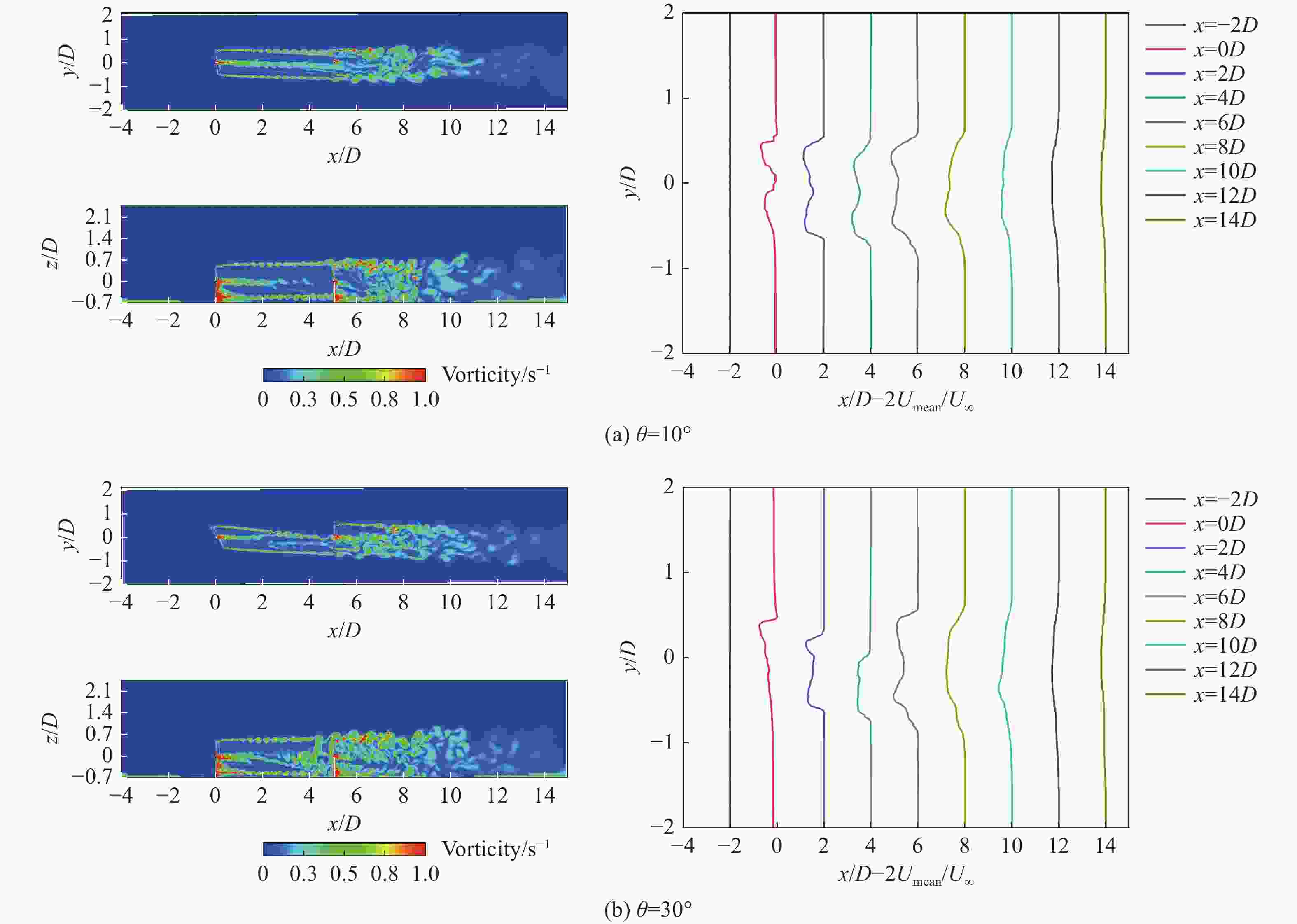
图 3 不同θ工况下双风力发电机平均尾流速度分布和流场涡量云图
Figure 3. Average wake velocity distribution and vorticity for dual wind turbines under various θ cases
由图2可知，随着上游风力发电机的偏航角逐渐增大，下游风力发电机的气动功率也随之增加。在θ=0°～20°的范围内，无论是下游风力发电机还是整体气动功率，都显示出随着偏航角的增加而逐步提升的现象。通过涡量云图可知在θ=10°时，如图3(a)所示，下游风力发电机几乎完全位于上游风力发电机尾流的干扰区域内，可以观察到显著的尾流干扰现象。当θ=20°时整体功率达到最大值，是由于上游风力发电机产生的尾流效应较为显著，导致流场风速持续降低。当θ=30°时，下游风力发电机仅有大约一半的尾流区域受到上游风力发电机尾流的影响，如图3(b)所示，速度较低的蓝绿色区域的面积也在逐步缩小，相对于θ=10°，下游风力发电机所遭受的尾流干扰有了显著的减轻。当θ=40°时尽管上游风力发电机的气动功率降至其额定功率的60%，下游风力发电机的气动性能会提升至接近额定功率的80%，这表明上游风力发电机的尾流不仅减少了下游风力发电机的入流风速，还增加了入流的湍流强度。
如图3平均尾流速度分布图所示，上游风力发电机的尾流作用在下游风力发电机的尾流范围会不断减小，尾流的相互作用逐渐减弱，但在叶尖中心线附近的速度仍然不足来流速度的一半，这表明由尾流相互作用引起的尾流叠加效应依然显著。
进一步比较不同偏航角度下串列双风力发电机的功率表现，可以观察到整体功率随着偏航角度的增加先上升后下降。θ=20°时，整体功率达到峰值，约为7.6 MW，此时整体功率损耗比降至28.3%。然而，随着偏航角度继续增大，整体功率开始下降。
-
图4展示了在不同塔架高差工况下的上下游风力发电机及串列双风力发电机的平均气动功率及整体功率提升比。
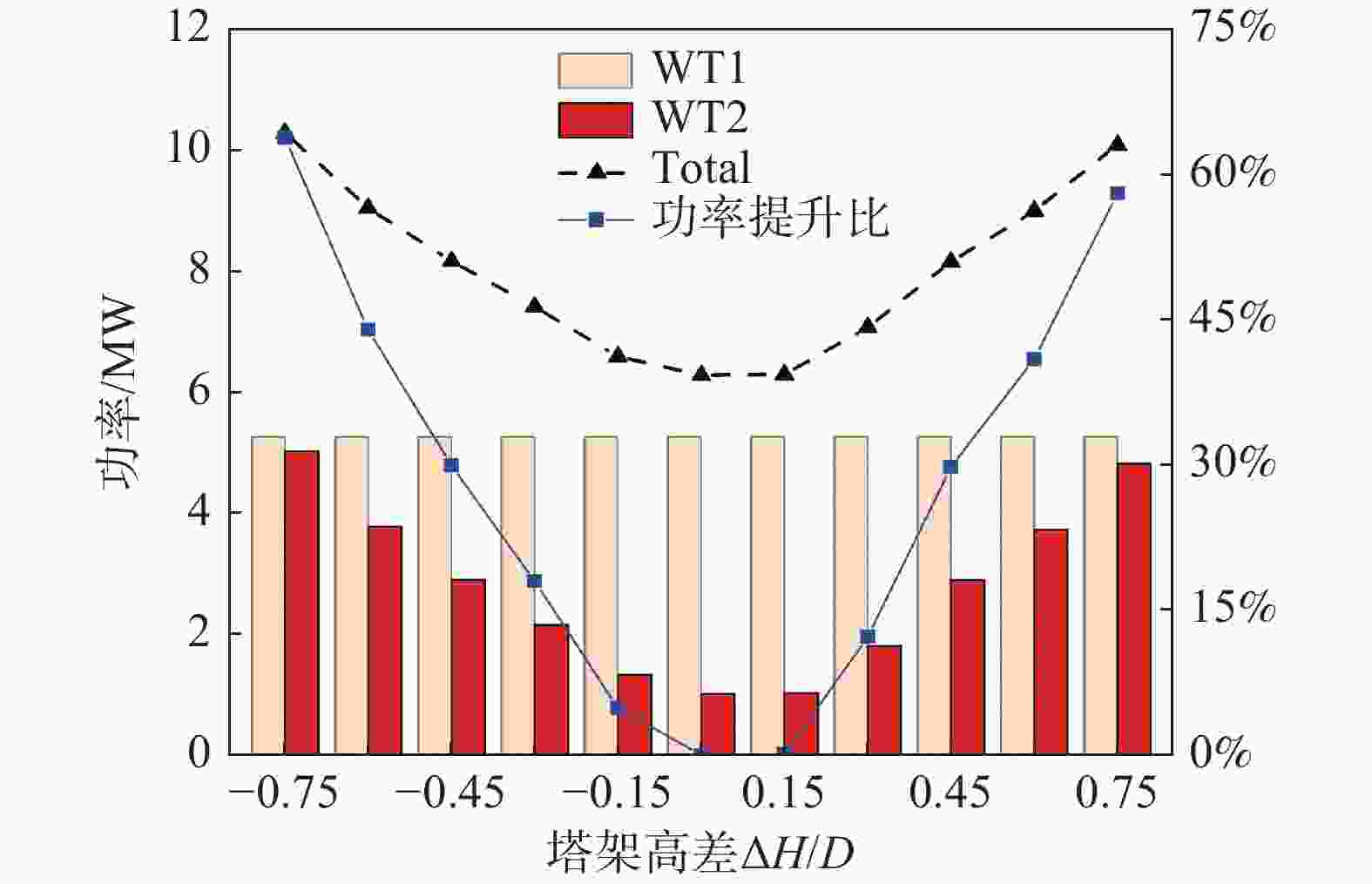
图 4 不同ΔH工况下双风力发电机平均气动功率及整体功率提升比
Figure 4. Average aerodynamic power and overall power gain ratio for dual wind turbines under various ΔH cases
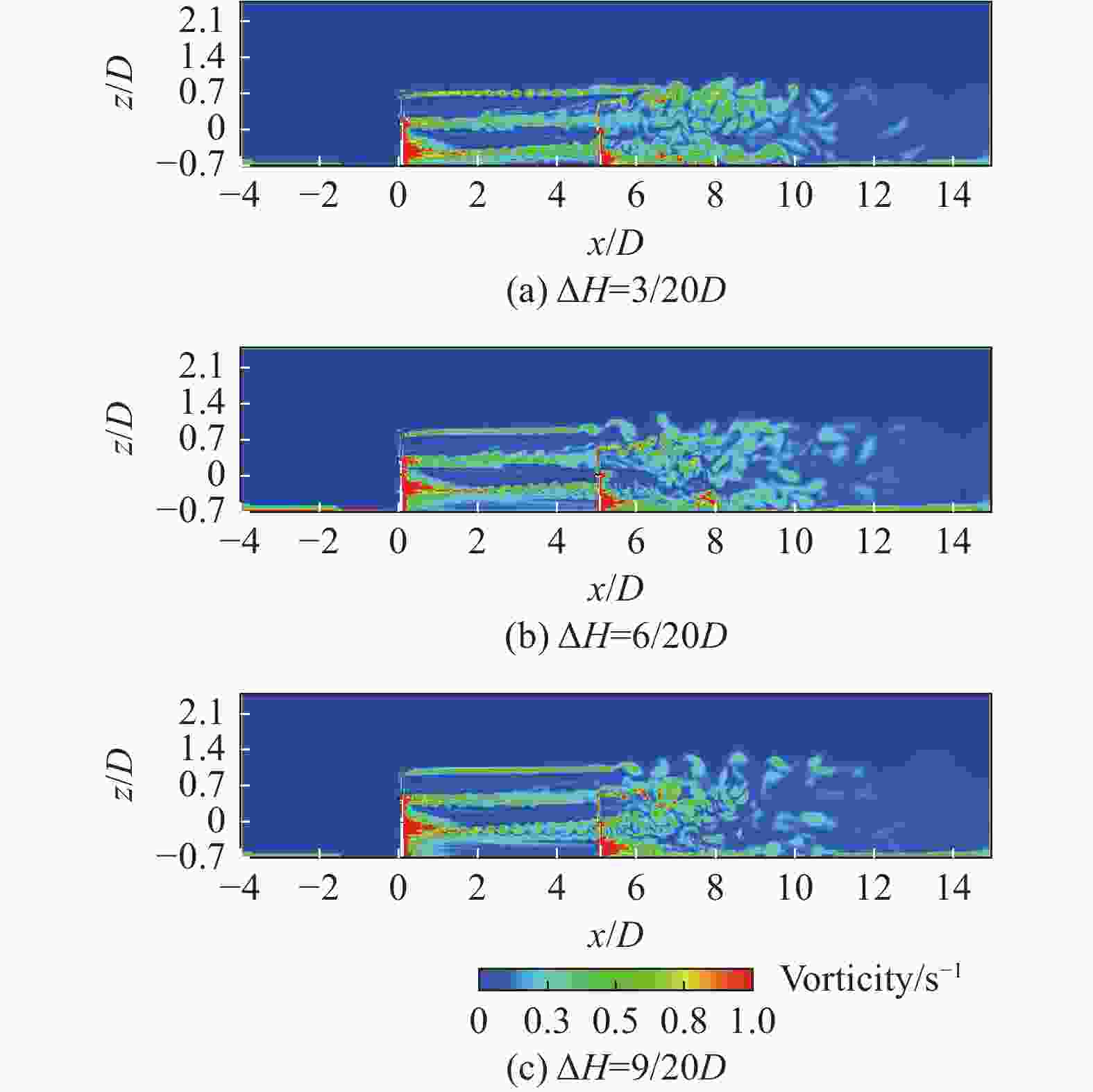
由图4可知，塔架高差为零的工况下，下游风力发电机功率提升比R=0。随着塔架高差的增加，上游风力发电机对下游风力发电机的干扰会逐渐减少，这使得下游风力发电机的输出功率增加，相应地，功率损失也随之减少。当ΔH=3/20D时，整体气动功率仅提高0.16%，如图5(a)所示，下游风力发电机基本还是完全处于上游风力发电机的尾流区域内，当ΔH=9/20D时，如图5(c)所示，未在上游风力发电机尾流区域的上部区域出现重叠，这意味着该区域未受上游风力发电机尾流影响，因此损失的功率会变小，可解释ΔH=9/20D功率提升比显著增加的原因。而当ΔH=−3/20D时，整体气动功率提高了4.94%，当ΔH=−6/20D时整体功率提升比R=17.99%，相对于提高上游风力发电机塔架高度的效果更好，而ΔH=±15/20D时，下游风力发电机功率提升比相差不大，且此时已经非常接近额定功率，因此增加塔架高差可以降低尾流效应对下游风力发电机的影响。
图 5 不同ΔH工况下双风力发电机流场涡量云图
Figure 5. Vorticity for dual wind turbines under various ΔH cases
-
图6展示了在不同横向间距工况下的上下游风力发电机及串列双风力发电机的平均气动功率及整体功率提升比。
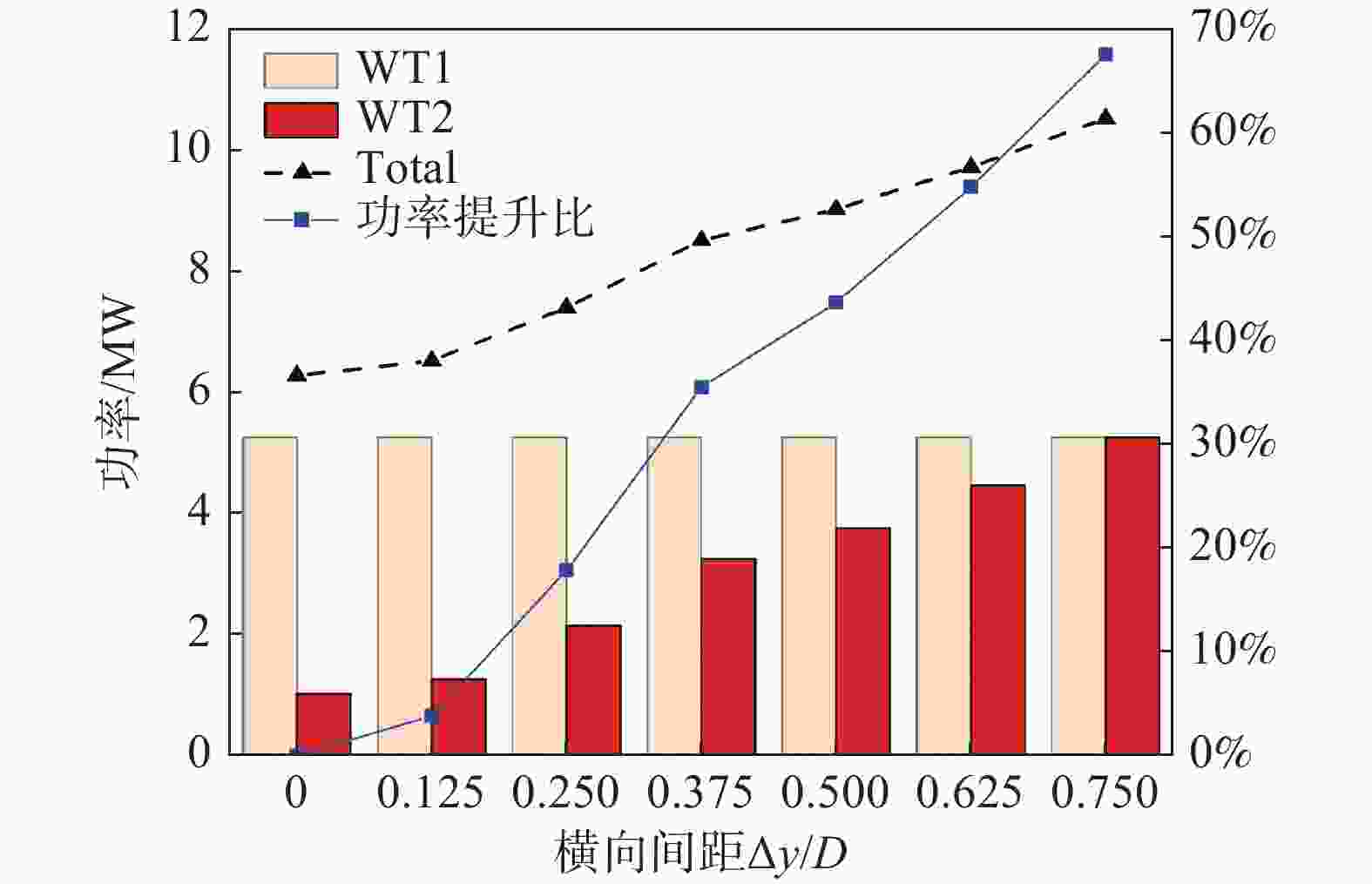
图 6 不同Δy工况下双风力发电机平均气动功率及整体功率提升比
Figure 6. Average aerodynamic power and overall power gain ratio for dual wind turbines under various Δy cases
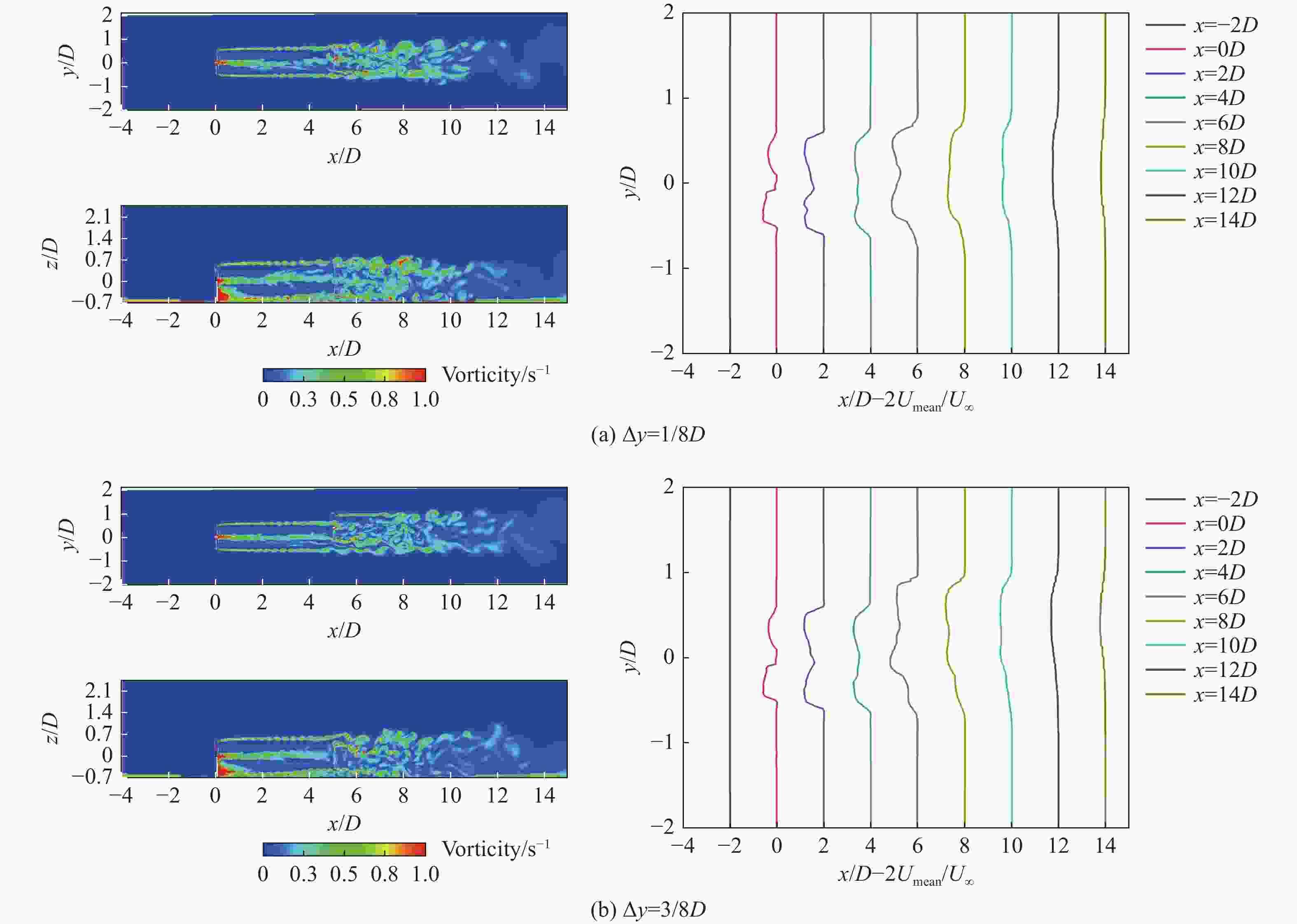
由图6可知，在没有调整横向间距的状态下，下游风力发电机几乎完全被包含在上游风力发电机的尾流影响范围内。在两个风轮平面相互重叠的区域，形成了一个极其复杂的尾流场，导致尾流速度显著下降，下游风力发电机受到明显的干扰，其气动功率大约降至1.02 W。当Δy=1/8D时，如图7(a)所示，下游风力发电机几乎完全处于上游风力发电机的尾流区域内，此时的功率提升率仅有3.82%，无明显优化作用。当Δy=2/8D时，下游风力发电机的气动功率增加了超过一倍，整体功率提升的比率达到了17.83%。再继续增加到Δy=3/8D时，即下游风机在偏移一定间距后，如图7(b)所示，在上游风力发电机尾流区域重叠部分减少，上游风机尾流经过其偏移位置处的尾流会继续周期性稳定向后发展，从而能解释Δy=3/8D时下游风机气动功率得到显著增加的情况。进一步增加到Δy=4/8D时，下游风力发电机的气动功率几乎增长了3倍，整体功率能提升43.63%。在增加到Δy=6/8D时，上游风力发电机的尾流不再对下游风力发电机产生干扰。
图 7 不同Δy工况下双风力发电机平均尾流速度分布和流场涡量云图
Figure 7. Average wake velocity distribution and vorticity flow plot for dual wind turbines under various Δy cases
-
图8展示了不同上游风力发电机偏航角与塔架高差组合工况下的风力发电机气动功率结果。整体功率提升率是串列双风力发电机在不同组合工况下的气动功率输出和在偏航角和塔架高差均为零工况下的气动功率输出的比值。
图 8 不同θ与ΔH工况组合时，双风力发电机气动功率结果
Figure 8. Aerodynamic power outcomes of dual wind turbines under various θ and ΔH cases
θ=10°～40°范围内，上游风力发电机气动功率逐渐降低，下游风力发电机的气动功率逐渐上升，整体气动功率呈现出先上升后下降的趋势。此时在保持上游风力发电机偏航角不变的情况下，增加下游风力发电机塔架高度会达到显著增加整体气动功率的效果，而当ΔH=−3/20D～ΔH=−9/20D时，上游风力发电机的气动功率基本维持不变，下游风力发电机的气动功率上升。随着上游风力发电机偏航角的增加，其气动功率会逐步降低，而下游风力发电机的气动功率则相应地增加。当θ=20°时，整体气动功率会达到一个峰值。这表明通过适当调整上游风力发电机的偏航角度，可以在一定程度上优化串列双风力发电机的气动性能。
相对于偏航角与塔架高差均为零的工况，当θ=10°、ΔH=−3/20D时，整体功率为6.40 MW，整体功率提升比仅为1.91%，没有明显的优化效果。而θ=20°～40°、ΔH=−3/20D～ΔH=−9/20D时，整体功率都能得到较大的提升。其中，在θ=20°、ΔH=−9/20D工况下，整体功率达到最大值8.04 MW，整体气动功率提升比达到最大值27.98%，能够达到接近额定功率的水平，有明显的优化效果。因此，在θ=20°、ΔH=−9/20D工况下，整体功率输出达到峰值，可以提高串列双风力发电机的发电效率。
-
图9展示了不同上游风力发电机偏航角和横向间距组合工况下串列双风力发电机的气动功率结果。
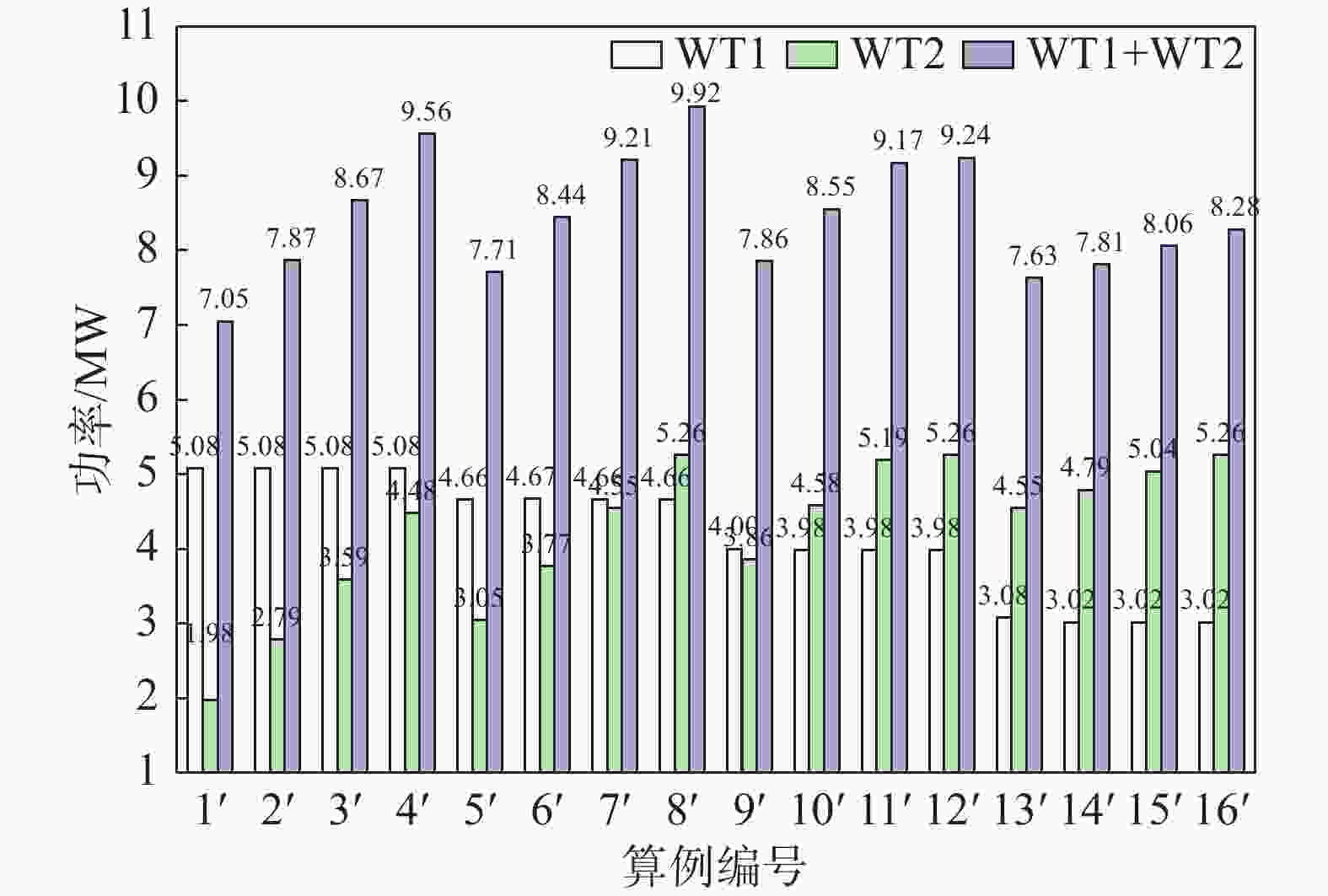
图 9 不同θ与Δy工况组合时，双风力发电机气动功率结果
Figure 9. Aerodynamic power outcomes of dual wind turbines under various θ and Δy cases
在θ=10°～40°范围内，上游风力发电机气动功率呈现出逐渐降低的趋势，下游风力发电机的气动功率不再受到上游尾流的显著干扰，气动功率呈现出上升趋势，整体气动功率也呈现出上升趋势，特别是当θ=40°时，其尾流对下游风力发电机的影响很小。而当Δy=1/8D～Δy=4/8D时，气动性能保持一致，尽管上游风力发电机的气动功率保持相对稳定，但下游风力发电机的气动功率却呈现出较大增长。这种尾流效应对下游风力发电机的性能有显著影响，既减少了其有效风速，又增加了入流的湍流强度。风力发电机偏航角不变时，增加风力发电机间的横向间距可以增加串列双风力发电机整体气动功率。
相对于偏航角与横向间距均为零的工况，当θ=10°、Δy=1/8D时，整体功率为7.05 MW，整体功率提升比仅为12%，没有明显的优化效果。而θ=20°～40°，Δy=1/8D～Δy=4/8D时，整体功率都能得到较大的提升，其中当θ=20°、Δy=4/8D时，整体功率达到最大值9.92 MW，整体气动功率提升比达到最大值57.91%，能够达到接近额定功率的水平。因此，在θ=20°、Δy=4/8D工况下，能够有效地减少串列双风力发电机间的尾流干扰，整体功率输出达到峰值。
-
图10展示了不同风力发电机塔架高差和横向间距组合工况下串列双风力发电机的气动功率结果。
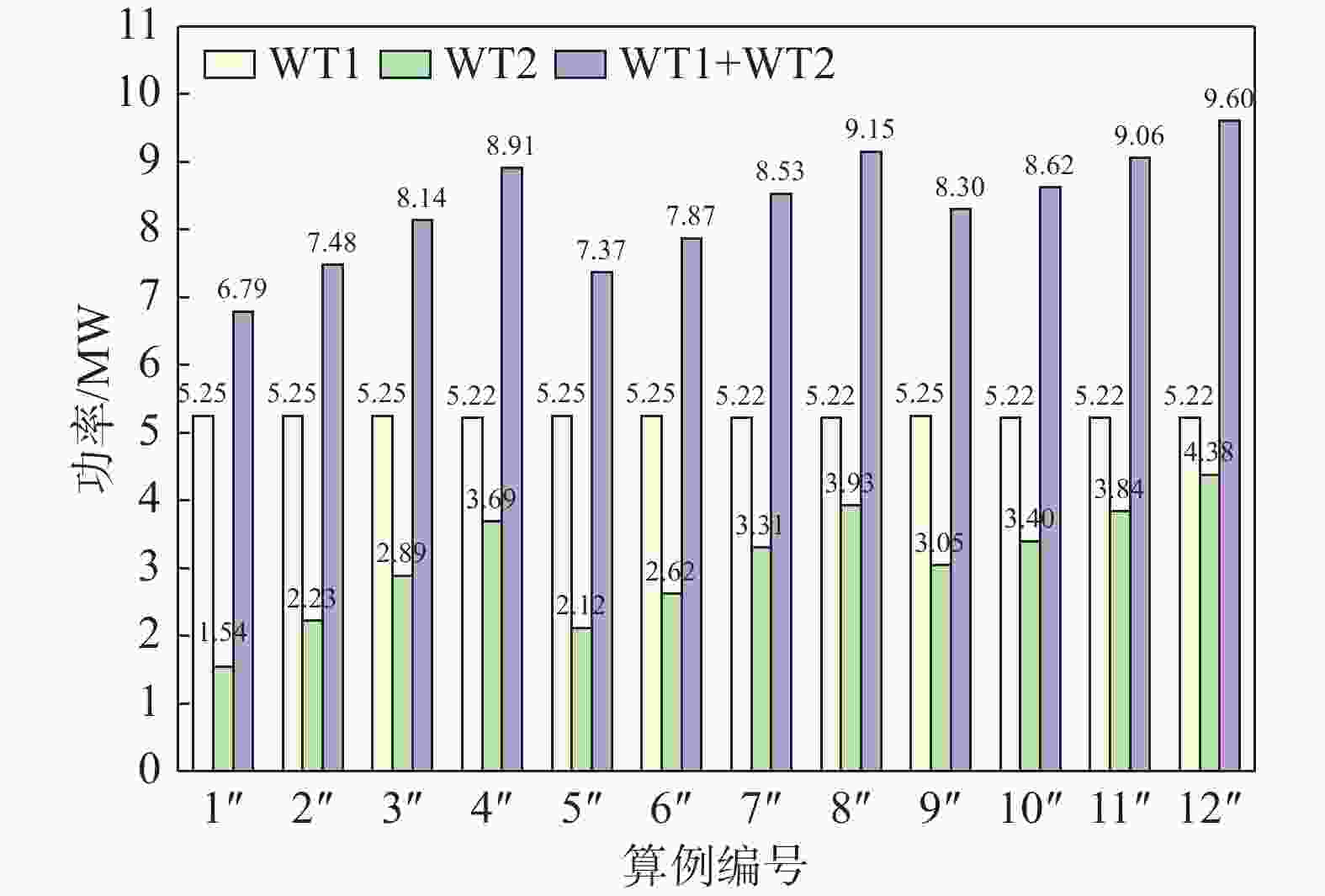
图 10 不同ΔH与Δy工况组合时，双风力发电机气动功率结果
Figure 10. Aerodynamic power outcomes of dual wind turbines under various ΔH and Δy cases
在ΔH=−3/20D～ΔH=−9/20D范围内，上游风力发电机的气动性能保持不变，下游风力发电机的气动功率在增加，这种变化导致整体气动功率也呈现出上升的趋势，这表明整体发电效率在提高。此时在保持塔架高差不变的情况下，增加横向间距会达到显著增加整体气动功率的效果，且在Δy=4/8D时达到最大。而从Δy=1/8D～Δy=4/8D时，气动性能保持一致，上游风力发电机气动功率几乎保持一致，下游风力发电机的气动功率呈现出上升趋势，此时在保持横向间距不变的情况下，增加塔架高差使上游风力发电机气动功率会逐渐减小，下游风力发电机气动功率会逐渐增加，会增加整体气动功率，在ΔH=−9/20D时达到最大。
相对于塔架高差与横向间距均为零的工况，当ΔH=−3/20D、Δy=1/8D时，整体功率为6.79 MW，整体功率提升比仅为8%，没有明显的优化效果；而在ΔH=−3/20D～ΔH=−9/20D、Δy=1/8D～Δy=4/8D范围内时，整体功率都能得到较大的提升。其中，在ΔH=−9/20D、Δy=4/8D工况时，整体功率达到最大值9.60 MW，整体功率提升比达到最大值52.87%，能够达到接近额定功率的水平，有明显的优化效果。因此，当ΔH=−9/20D、Δy=4/8D时，整体功率输出达到峰值。
-
为了对比单一尾流干扰抑制策略及组合尾流干扰抑制策略对风力发电机气动性能的优化情况，在本节中对2种不同尾流干扰抑制策略进行了分析。
-
在表8中，展示了在不同工况下串列双风力发电机整体气动功率及功率提升比，其中工况Ⅰ表示只考虑偏航角情况；工况Ⅱ表示只考虑塔架高差情况；工况Ⅳ表示不同偏航角与塔架高差组合情况。
表 8 不同θ与ΔH工况组合时，双风力发电机整体功率及功率提升比变化情况
Table 8. The variation of overall power and power augmentation rate for dual wind turbine under various θ and ΔH cases
工况 θ/(°) ΔH 功率/
MW功率
提升比/%Ⅰ 10 0 6.56 4 Ⅱ 0 −3/20D 6.58 5 Ⅳ 10 −3/20D 6.4 2 Ⅰ 10 0 6.56 4 Ⅱ 0 −6/20D 7.48 19 Ⅳ 10 −6/20D 7.18 14 Ⅰ 10 0 6.56 4 Ⅱ 0 −9/20D 8.31 32 Ⅳ 10 −9/20D 8.01 28 Ⅰ 20 0 7.6 21 Ⅱ 0 −3/20D 6.58 5 Ⅳ 20 −3/20D 7.08 13 Ⅰ 20 0 7.6 21 Ⅱ 0 −6/20D 7.48 19 Ⅳ 20 −6/20D 7.64 22 Ⅰ 20 0 7.6 21 Ⅱ 0 −9/20D 8.31 32 Ⅳ 20 −9/20D 8.04 28 Ⅰ 30 0 7.47 19 Ⅱ 0 −3/20D 6.58 5 Ⅳ 30 −3/20D 7.25 15 Ⅰ 30 0 7.47 19 Ⅱ 0 −6/20D 7.48 19 Ⅳ 30 −6/20D 7.43 18 Ⅰ 30 0 7.47 19 Ⅱ 0 −9/20D 8.31 32 Ⅳ 30 −9/20D 7.82 25 Ⅰ 40 0 7.35 17 Ⅱ 0 −3/20D 6.58 5 Ⅳ 40 −3/20D 7.03 12 Ⅰ 40 0 7.35 17 Ⅱ 0 −6/20D 7.48 19 Ⅳ 40 −6/20D 7.01 12 Ⅰ 40 0 7.35 17 Ⅱ 0 −9/20D 8.31 32 Ⅳ 40 −9/20D 7.24 15 为了阐明风力发电机功率随着偏航角和塔架高差变化的关系，对轮毂高度水平面上的平均尾流速度及流场涡量分布进行了深入分析，如图11所示。
图 11 不同θ与ΔH工况组合时，双风力发电机平均尾流速度分布和流场涡量云图
Figure 11. Average wake velocity distribution and vorticity flow plot for dual wind turbines under various θ and ΔH cases
在固定偏航角的情况下，将塔架高差设为单一的影响因素，整体功率会随着塔架高差的增加而增加。在固定塔架高度的情况下，将上游风力发电机的偏航角设为单一的影响因素，在θ=20°的条件下，气动功率达到峰值，整体气动功率也随着偏航角的增加而先增后减，是因为尽管下游风力发电机的气动功率随着偏航角的增加而持续增长。但当θ=30°和θ=40°时，如图11(c)、图11(d)所示，在风力发电机叶尖附近的尾流区域，以及在2D和4D的位置，尾流速度曲线均出现了一个向左偏移的峰值，峰值接近1，这意味着在风轮叶尖处的风速大约是来流速度的一半，即尾流导致风速减少了约50%，此时下游风力发电机气动功率的增长幅度小于上游风力发电机气动功率减少的幅度，导致整体功率提升比率下降。
相对于偏航角和塔架高差均为零的工况，当θ=10°、ΔH=−3/20D时，整体功率为6.40 MW，功率提升比仅为2%，没有明显的优化效果。而在第2节中可知，单独改变风力发电机偏航角与塔架高差分别为θ=10°和ΔH=−3/20D时其整体功率提升比也表现出无明显效果。而在保持塔架高差不变，在θ=10°～40°范围内，以及保持偏航角不变，从ΔH=−3/20D～ΔH=−9/20D时，整体功率提升明显。
如图11所示，随着偏航角和塔架高差的增加，下游风力发电机受到上游风力发电机尾流影响的区域逐渐缩小。但下游风力发电机的旋转区域中仍有部分始终处于上游风力发电机尾流的影响之下，导致气动功率存在一定的损失。特别地，在θ=20°和ΔH=−6/20D工况下，整体功率达到7.64 MW，整体功率提升率为22%，这比在单一尾流干扰抑制策略情况下最佳工况下的功率还要高。但在其他情况下，整体功率都低于单一尾流干扰抑制策略情况下最佳工况下的功率。随着塔架高差的增加，下游风力发电机逐渐移出上游风力发电机的尾流影响区域，当ΔH=−9/20D时几乎不受上游风力发电机尾流的影响，这与在θ=20°、ΔH=−9/20D工况下游风力发电机的气动功率损耗较小的结果一致。
通过观察图11中轴向速度沿横向位置的分布曲线，可以更全面地了解串列双风力发电机尾流相互干扰的区域范围。当上游风力发电机偏航角较小与塔架高差较小时，尾流的膨胀效应会导致干扰区域的扩大。
-
在表9中，展示了在不同工况下风力发电机整体气动功率及功率提升比，其中工况Ⅰ表示只考虑偏航角情况；工况Ⅲ表示只考虑横向间距情况；工况Ⅴ表示不同偏航角与横向间距组合情况。为了阐明风力发电机功率随着偏航角和横向间距变化的关系，对轮毂高度水平面上的平均尾流速度及流场涡量分布进行了深入分析如图12所示。
表 9 不同θ与Δy工况组合时，双风力发电机整体功率及功率提升比变化情况
Table 9. The variation of overall power and power augmentation rate for dual wind turbine under various θ and Δy cases
工况 θ/(°) Δy 功率/
MW功率
提升比/%Ⅰ 10 0 6.56 4 Ⅲ 0 1/8D 6.52 4 Ⅴ 10 1/8D 7.05 12 Ⅰ 10 0 6.56 4 Ⅲ 0 2/8D 7.4 18 Ⅴ 10 2/8D 7.87 25 Ⅰ 10 0 6.56 4 Ⅲ 0 3/8D 8.51 36 Ⅴ 10 3/8D 8.67 38 Ⅰ 10 0 6.56 4 Ⅲ 0 4/8D 9.02 44 Ⅴ 10 4/8D 9.56 52 Ⅰ 20 0 7.6 21 Ⅲ 0 1/8D 6.52 4 Ⅴ 20 1/8D 7.71 23 Ⅰ 20 0 7.6 21 Ⅲ 0 2/8D 7.4 18 Ⅴ 20 2/8D 8.44 34 Ⅰ 20 0 7.6 21 Ⅲ 0 3/8D 8.51 36 Ⅴ 20 3/8D 9.21 47 Ⅰ 20 0 7.6 21 Ⅲ 0 4/8D 9.02 44 Ⅴ 20 4/8D 9.92 58 Ⅰ 30 0 7.47 19 Ⅲ 0 1/8D 6.52 4 Ⅴ 30 1/8D 7.86 25 Ⅰ 30 0 7.47 19 Ⅲ 0 2/8D 7.4 18 Ⅴ 30 2/8D 8.55 36 Ⅰ 30 0 7.47 19 Ⅲ 0 3/8D 8.51 36 Ⅴ 30 3/8D 9.17 46 Ⅰ 30 0 7.47 19 Ⅲ 0 4/8D 9.02 44 Ⅴ 30 4/8D 9.24 47 Ⅰ 40 0 7.35 17 Ⅲ 0 1/8D 6.52 4 Ⅴ 40 1/8D 7.63 21 Ⅰ 40 0 7.35 17 Ⅲ 0 2/8D 7.4 18 Ⅴ 40 2/8D 7.81 24 Ⅰ 40 0 7.35 17 Ⅲ 0 3/8D 8.51 36 Ⅴ 40 3/8D 8.06 28 Ⅰ 40 0 7.35 17 Ⅲ 0 4/8D 9.02 44 Ⅴ 40 4/8D 8.28 32 
图 12 不同θ与Δy工况组合时，双风力发电机平均尾流速度分布和流场涡量云图
Figure 12. Average wake velocity distribution and vorticity flow plot for dual wind turbines under various θ and Δy cases
在固定偏航角的情况下，将横向间距设为单一的影响因素，在Δy=1/8D时，功率提升比仅为4%，无明显优化效果，在Δy=4/8D时达到最大功率9.02 MW，功率提升比也达到最大值44%，整体功率会随着横向间距的增加而逐渐增加。在保持横向间距不变的情况下，如果将上游风力发电机的偏航角度作为唯一的影响因素，那么在θ=10°时，整体功率提升比率仅为4%，这一变化并不显著，表明优化效果有限。然而，当θ=20°时，总功率达到最大值7.60 MW，功率提升比率也达到最高21%，此时，气动功率达到峰值，但随着偏航角的进一步增加，整体气动功率会先增加后减少，显示出一个先升后降的趋势。这表明在优化风力发电机的布局和偏航角度时，存在一个最佳偏航角度，超过这个角度后，整体功率反而会下降。
相对于偏航角和横向间距均为零的工况，当θ=10°、Δy=1/8D时，风力发电机整体功率为7.05 MW，功率提升比仅为12%，没有明显的优化效果。而在第2节中可知，单独改变风力发电机偏航角与横向间距分别为θ=10°和Δy=1/8D时其整体功率提升比也表现出无明显效果的现象。而仅改变θ=10°～40°，以及仅改变Δy=1/8D～Δy=4/8D时，整体功率提升比都能得到较大的提升。随着偏航角和横向间距的增加，下游风力发电机受到上游风力发电机尾流的影响逐渐减小。然而，下游风力发电机的旋转区域中仍然有一部分始终处于上游风力发电机尾流的影响范围内，导致气动功率存在一定的损失。这种现象表明，尽管通过调整偏航角和增加横向间距可以减少尾流干扰，但完全消除尾流影响仍具有挑战性，风力发电机的气动性能优化仍有进一步的提升空间。当θ=20°、Δy=4/8D时整体功率达到最大9.92 MW，提升率也达到最大值58%，极大地提升了优化效果。
随着上下游风力发电机间偏航角和横向间距的增加，如图12所示，通过风力发电机流场涡量云图可以看出，随着下游风力发电机逐渐远离上游风力发电机的尾流覆盖范围，它们受到的尾流影响开始减弱，当θ=20°、Δy=4/8D时几乎不受上游风力发电机尾流的影响，这与该工况下游风力发电机的气动功率损耗较小的结果一致。
-
表10展示了在不同工况下风力发电机整体气动功率及功率提升比，其中工况Ⅱ表示只考虑塔架高差情况；工况Ⅲ表示只考虑横向间距况；工况Ⅵ表示不同ΔH与Δy组合情况。为了阐明风力发电机功率随着塔架高差和横向间距变化的关系，对轮毂高度水平面上的平均尾流速度及流场涡量分布进行了深入分析，如图13所示。
表 10 不同ΔH与Δy工况组合时，双风力发电机整体功率及功率提升比变化情况
Table 10. The variation of overall power and power augmentation rate for dual wind turbine under various ΔH and Δy cases
工况 ΔH Δy 功率
/MW功率
提升比/%Ⅱ −3/20D 0 6.58 5 Ⅲ 0 1/8D 6.52 4 Ⅵ −3/20D 1/8D 6.79 8 Ⅱ −3/20D 0 6.58 5 Ⅲ 0 2/8D 7.4 18 Ⅵ −3/20D 2/8D 7.48 19 Ⅱ −3/20D 0 6.58 5 Ⅲ 0 3/8D 8.51 36 Ⅵ −3/20D 3/8D 8.14 30 Ⅱ −3/20D 0 6.58 5 Ⅲ 0 4/8D 9.02 44 Ⅵ −3/20D 4/8D 8.91 42 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 1/8D 6.52 4 Ⅵ −6/20D 1/8D 7.37 17 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 2/8D 7.4 18 Ⅵ −6/20D 2/8D 7.87 25 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 3/8D 8.51 36 Ⅵ −6/20D 3/8D 8.53 36 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 4/8D 9.02 44 Ⅵ −6/20D 4/8D 9.15 46 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 1/8D 6.52 4 Ⅵ −9/20D 1/8D 8.3 32 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 2/8D 7.4 18 Ⅵ −9/20D 2/8D 8.62 37 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 3/8D 8.51 36 Ⅵ −9/20D 3/8D 9.06 44 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 4/8D 9.02 44 Ⅵ −9/20D 4/8D 9.6 53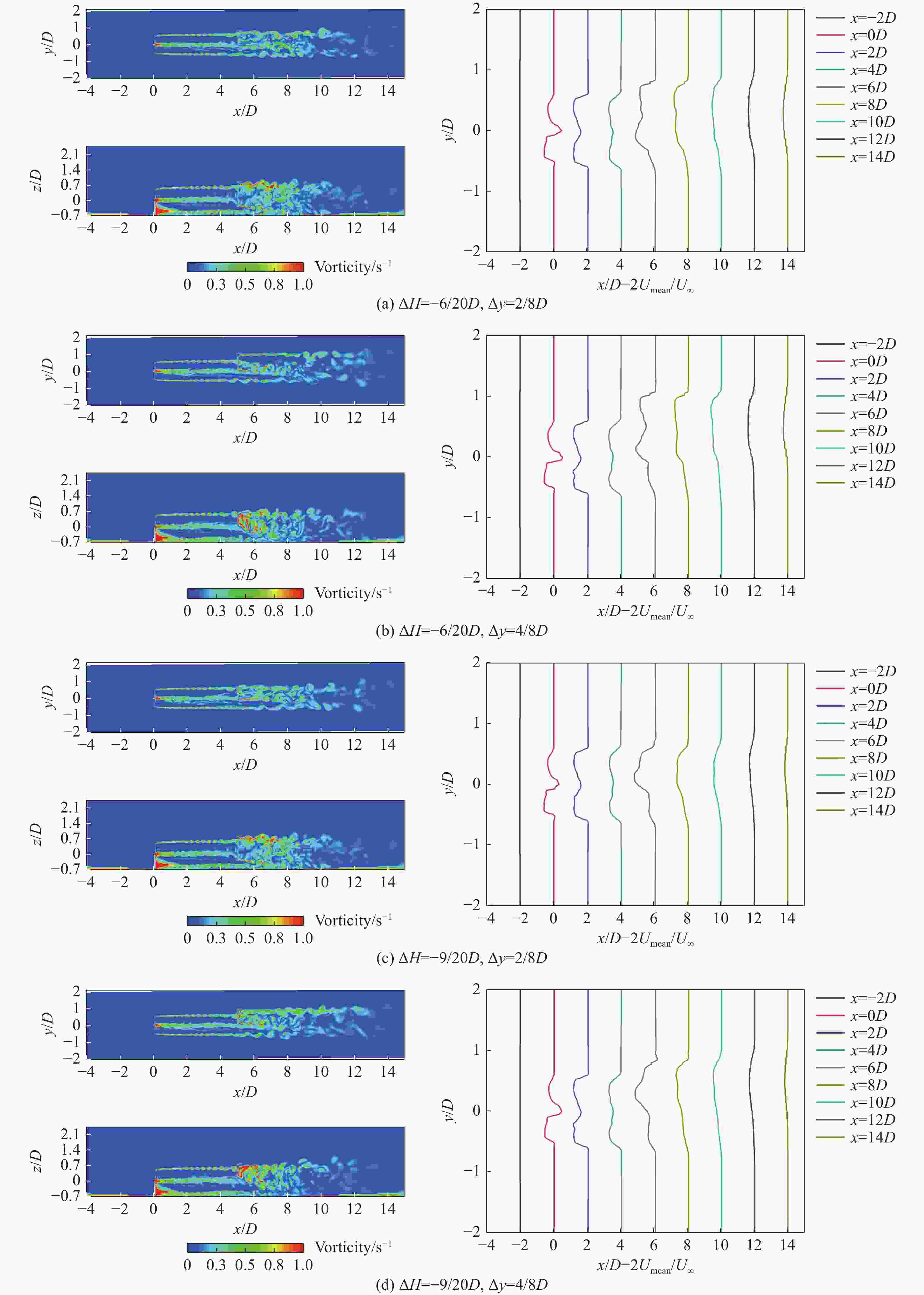 
图 13 不同ΔH与Δy工况组合时，串列双风力发电机平均尾流速度分布和流场涡量云图
Figure 13. Average wake velocity distribution and vorticity flow plot for dual wind turbines in tandem arrangement under various ΔH and Δy cases
在固定塔架高差的情况下，将横向间距设为单一的影响因素，在Δy=1/8D时，功率仅为6.52 MW，功率提升比仅为4%，无明显优化效果，在Δy=4/8D工况下达到最大功率9.02 MW，功率提升比也达到最大44%，整体功率会随着横向间距的增加而逐渐增加。在固定横向间距的情况下，将塔架高差设为单一的影响因素，在ΔH=−3/20D工况下功率仅为6.58 MW，功率提升比仅为5%，无明显优化效果，整体功率在ΔH=−9/20D工况下达到最大为8.31 MW，提升比也只达到8%，随着塔架高差的增加整体气动功率会有小幅增加，无明显优化效果。
相对于塔架高差与横向间距均为0的工况，当ΔH=−3/20D、Δy=1/8D时，整体功率为6.79 MW，功率提升比仅为8%，没有明显的优化效果。而在第2节中可知，单独改变风力发电机塔架高差与横向间距分别为ΔH=−3/20D和Δy=1/8D时其整体功率提升比也表现出无明显效果的现象。而仅改变风力发电机塔架高差（ΔH=−3/20D～ΔH=−9/20D），以及仅改变风力发电机横向间距从（Δy=1/8D～Δy=4/8D）时，风力发电机整体功率提升显著。在ΔH=−9/20D、Δy=4/8D工况下风力发电机整体功率达到最大9.60 MW，提升率也达到最大值53%，极大地提高了风力发电机的优化效果。
如图13所示，随着上下游风力发电机间塔架高差和横向间距的增加，它们受到的尾流影响开始减弱，其平均尾流速度在ΔH=−9/20D、Δy=4/8D时几乎不受上游风力发电机尾流的影响，这与在该工况下游风力发电机的气动功率损耗较小的结果一致。
-
本文对上游风力发电机偏航角分别与下游风力发电机塔架高差、横向间距在单一及组合尾流干扰抑制策略下风力发电机的气动性能进行了研究，详细阐述了串列双风力发电机的尾流情况及气动性能优化方法，得到了以下主要结论：
1）在维持风力发电机偏航角稳定的情况下，增加塔架高差或横向间距能有效降低尾流效应，提高功率。反之，若调整偏航角，随着其增加，整体的气动功率会先上升后下降。在考虑最优偏航角布置时，可以考虑在偏航角20°以下的区间内进行计算。
2）通过调整上游风力发电机的偏航角或采用上下游风机错列布局，可以减弱尾流影响，虽然这会降低上游风力发电机的气动功率输出，但能够显著改善下游风力发电机的运行环境，提升其气动功率输出，从而增强风力发电机整体的发电效率。
3）通过分析单一以及组合尾流干扰抑制策略对风力发电机气动功率的影响，结果显示它们之间存在非线性关系。这种非线性体现在，无论是增加上游风力发电机的偏航角，还是增加塔架高差或横向间距，风力发电机的总功率并不会简单地随着这些变量的增加而线性增长。
本文研究结果在风电场规划设计、风力发电机组的运行与维护中具有一定的指导意义，尤其是在考虑风电场内风力发电机组间相互影响时。将来深化研究的内容如下：分析风切变、湍流度、大气边界层热稳定性等环境因素对风力发电机尾流效应的影响，以及如何通过控制策略进行适应性调整。另外，考虑不同机组间的尾流干扰，优化机组间距、排布方式等，减少尾流损失，提高整个风电场的发电效率。这些研究成果将有助于进一步提升风力发电机组的气动性能，优化风电场的总体设计，降低风电成本，提高风能利用效率。
广 告 封面图片：具身智能，御风驭光 ——“AI+气象”赋能“气候韧性新型能源体系”----------- 封一 华能汕头勒门（二）海上风电项目---------------------------------------------------------------------- 封二 广西防城港海上风电示范项目---------------------------------------------------------------------------- 封三 中国能源建设集团广东省电力设计研究院有限公司------------------------------------------------ 封四
Impact of Wake Interference Suppression Strategies on the Aerodynamic Performance of Twin Wind Turbines
-
摘要:
目的 以NREL-5MW风力发电机为研究对象，采用基于对上游风力发电机偏航角（θ）与下游风力发电机塔架高差（ΔH）以及横向间距（Δy）的单一及组合的控制策略，研究两风机之间的复杂尾流干扰效应。 方法 通过数值模拟两风机的部分尾流相互干扰现象分析两风机的气动功率、尾流平均速度以及尾流干扰效应提高整个风电场发电效率。 结果 研究结果表明：实施组合策略时，尤其是在θ=20°的基础上，调整横向间距Δy=4D和Δy=8D时，风力发电机的整体功率及其提升比实现了最大化。 结论 通过改变上游风力发电机的偏航角或者上下游风机错列布置等尾流效应抑制策略，降低上游风力发电机的功率输出，改善上游风力发电机尾流的效应，可以提高下游风力发电机的气动功率输出，提高风力发电机整体发电功率，较大幅度地提高风力发电机的发电效率，为大规模风电场的布置优化提供了一定的数值模拟支撑。 Abstract:Objective The paper takes the NREL-5MW wind turbine as the research object, adopts the control strategy based on the single and combination of the yaw angle(θ) of the upstream wind turbine and the tower height(ΔH) difference of the downstream wind turbine as well as the lateral spacing(Δy), researches the complex wake interference effect between the two wind turbines. Method Numerically simulated the part of the wake interfering phenomenon between the two wind turbines, analyzed the aerodynamic power of the two wind turbines, the average speed of the wake flow, and the effect of the wake interference to improve the power generation of the whole wind power field efficiency of the whole wind farm. Result The results show that the overall power of the wind turbine and its enhancement ratio are maximized when the combined strategy is implemented, especially when adjusting the lateral spacing Δy=4D or Δy=8D on the basis of θ=20°. Conclusion By changing the yaw angle of the upstream wind turbine or the upstream and downstream wind turbines staggered arrangement and other wake effect inhibition strategies, the power output of the upstream wind turbine is reduced and the effect of the wake of the upstream wind turbine is improved, which can improve the aerodynamic power output of the downstream wind turbine and the overall power generation of the wind turbine, and improve the power generation efficiency of the wind turbine in a relatively large scale, and provide a certain degree of numerical simulation for the optimization of the arrangement of large-scale wind farms support. -
图 1 串列布置双风力发电机计算模型示意图
Fig. 1 Schematic diagram of the computational model for tandem-arranged dual wind turbines
图 2 不同θ工况下双风力发电机平均气动功率及整体功率提升比
Fig. 2 Average aerodynamic power and overall power gain ratio for dual wind turbines under various θ cases
图 3 不同θ工况下双风力发电机平均尾流速度分布和流场涡量云图
Fig. 3 Average wake velocity distribution and vorticity for dual wind turbines under various θ cases
图 4 不同ΔH工况下双风力发电机平均气动功率及整体功率提升比
Fig. 4 Average aerodynamic power and overall power gain ratio for dual wind turbines under various ΔH cases
图 5 不同ΔH工况下双风力发电机流场涡量云图
Fig. 5 Vorticity for dual wind turbines under various ΔH cases
图 6 不同Δy工况下双风力发电机平均气动功率及整体功率提升比
Fig. 6 Average aerodynamic power and overall power gain ratio for dual wind turbines under various Δy cases
图 7 不同Δy工况下双风力发电机平均尾流速度分布和流场涡量云图
Fig. 7 Average wake velocity distribution and vorticity flow plot for dual wind turbines under various Δy cases
图 8 不同θ与ΔH工况组合时，双风力发电机气动功率结果
Fig. 8 Aerodynamic power outcomes of dual wind turbines under various θ and ΔH cases
图 9 不同θ与Δy工况组合时，双风力发电机气动功率结果
Fig. 9 Aerodynamic power outcomes of dual wind turbines under various θ and Δy cases
图 10 不同ΔH与Δy工况组合时，双风力发电机气动功率结果
Fig. 10 Aerodynamic power outcomes of dual wind turbines under various ΔH and Δy cases
图 11 不同θ与ΔH工况组合时，双风力发电机平均尾流速度分布和流场涡量云图
Fig. 11 Average wake velocity distribution and vorticity flow plot for dual wind turbines under various θ and ΔH cases
图 12 不同θ与Δy工况组合时，双风力发电机平均尾流速度分布和流场涡量云图
Fig. 12 Average wake velocity distribution and vorticity flow plot for dual wind turbines under various θ and Δy cases
图 13 不同ΔH与Δy工况组合时，串列双风力发电机平均尾流速度分布和流场涡量云图
Fig. 13 Average wake velocity distribution and vorticity flow plot for dual wind turbines in tandem arrangement under various ΔH and Δy cases
表 1 3种不同网格下的风力发电机推力和功率数值
Tab. 1. Values of wind turbine thrust and power for three different grids
网格 网格
总数/万流体域
网格/万旋转区域
网格/万推力/kN 功率/MW Mesh1 1580 780 800 707
(0.6%)5.22
(1.1%)Mesh2 2000 780 1220 711
(0.0%)5.26
(0.4%)Mesh3 2 590 780 1810 711
(0.0%)5.28
(0.3%)
下载: 导出CSV
表 2 本文结果与文献结果对比
Tab. 2. Comparison of the numerical results with the published numerical results
下载: 导出CSV
表 3 本文结果与文献结果对比
Tab. 3. Comparison of the numerical results with the published numerical results
下载: 导出CSV
表 4 不同变量工况下算例参数设置
Tab. 4. Parameter settings for case studies under various variable cases
变量 工况 Δx θ/(°) Δy θ A1 5D 10 0 A2 20 0 A3 30 0 A4 40 0 Δy B1 5D 0 1/8D B2 0 2/8D B3 0 3/8D B4 0 4/8D B5 0 5/8D B6 0 6/8D 变量 工况 H1/m H2/m ΔH ΔH C1 90 184.5 −15/20D C2 90 165.6 −12/20D C3 90 146.7 −9/20D C4 90 127.8 −6/20D C5 90 108.9 −3/20D C0 90 90 0 C6 108.9 90 +3/20D C7 127.8 90 +6/20D C8 146.7 90 +9/20D C9 165.6 90 +12/20D C10 184.5 90 +15/20D
下载: 导出CSV
表 5 不同θ与ΔH工况组合时，算例参数设置
Tab. 5. Parameter settings at different θ and ΔH cases
算例编号 Δx θ/(°) ΔH 1 5D 10 −3/20D 2 5D 10 −6/20D 3 5D 10 −9/20D 4 5D 20 −3/20D 5 5D 20 −6/20D 6 5D 20 −9/20D 7 5D 30 −3/20D 8 5D 30 −6/20D 9 5D 30 −9/20D 10 5D 40 −3/20D 11 5D 40 −6/20D 12 5D 40 −9/20D
下载: 导出CSV
表 6 不同θ与Δy工况组合时，算例参数设置
Tab. 6. Parameter settings at different θ and Δy cases
算例编号 Δx θ/(°) Δy 1′ 5D 10 1/8D 2′ 5D 10 2/8D 3′ 5D 10 3/8D 4′ 5D 10 4/8D 5′ 5D 20 1/8D 6′ 5D 20 2/8D 7′ 5D 20 3/8D 8′ 5D 20 4/8D 9′ 5D 30 1/8D 10′ 5D 30 2/8D 11′ 5D 30 3/8D 12′ 5D 30 4/8D 13′ 5D 40 1/8D 14′ 5D 40 2/8D 15′ 5D 40 3/8D 16′ 5D 40 4/8D
下载: 导出CSV
表 7 不同ΔH与Δy工况组合时，算例参数设置
Tab. 7. Parameter settings at different ΔH and Δy cases
算例编号 Δx ΔH Δy 1′′ 5D −3/20D 1/8D 2′′ 5D −3/20D 2/8D 3′′ 5D −3/20D 3/8D 4′′ 5D −3/20D 4/8D 5′′ 5D −6/20D 1/8D 6′′ 5D −6/20D 2/8D 7′′ 5D −6/20D 3/8D 8′′ 5D −6/20D 4/8D 9′′ 5D −9/20D 1/8D 10′′ 5D −9/20D 2/8D 11′′ 5D −9/20D 3/8D 12′′ 5D −9/20D 4/8D
下载: 导出CSV
表 8 不同θ与ΔH工况组合时，双风力发电机整体功率及功率提升比变化情况
Tab. 8. The variation of overall power and power augmentation rate for dual wind turbine under various θ and ΔH cases
工况 θ/(°) ΔH 功率/
MW功率
提升比/%Ⅰ 10 0 6.56 4 Ⅱ 0 −3/20D 6.58 5 Ⅳ 10 −3/20D 6.4 2 Ⅰ 10 0 6.56 4 Ⅱ 0 −6/20D 7.48 19 Ⅳ 10 −6/20D 7.18 14 Ⅰ 10 0 6.56 4 Ⅱ 0 −9/20D 8.31 32 Ⅳ 10 −9/20D 8.01 28 Ⅰ 20 0 7.6 21 Ⅱ 0 −3/20D 6.58 5 Ⅳ 20 −3/20D 7.08 13 Ⅰ 20 0 7.6 21 Ⅱ 0 −6/20D 7.48 19 Ⅳ 20 −6/20D 7.64 22 Ⅰ 20 0 7.6 21 Ⅱ 0 −9/20D 8.31 32 Ⅳ 20 −9/20D 8.04 28 Ⅰ 30 0 7.47 19 Ⅱ 0 −3/20D 6.58 5 Ⅳ 30 −3/20D 7.25 15 Ⅰ 30 0 7.47 19 Ⅱ 0 −6/20D 7.48 19 Ⅳ 30 −6/20D 7.43 18 Ⅰ 30 0 7.47 19 Ⅱ 0 −9/20D 8.31 32 Ⅳ 30 −9/20D 7.82 25 Ⅰ 40 0 7.35 17 Ⅱ 0 −3/20D 6.58 5 Ⅳ 40 −3/20D 7.03 12 Ⅰ 40 0 7.35 17 Ⅱ 0 −6/20D 7.48 19 Ⅳ 40 −6/20D 7.01 12 Ⅰ 40 0 7.35 17 Ⅱ 0 −9/20D 8.31 32 Ⅳ 40 −9/20D 7.24 15
下载: 导出CSV
表 9 不同θ与Δy工况组合时，双风力发电机整体功率及功率提升比变化情况
Tab. 9. The variation of overall power and power augmentation rate for dual wind turbine under various θ and Δy cases
工况 θ/(°) Δy 功率/
MW功率
提升比/%Ⅰ 10 0 6.56 4 Ⅲ 0 1/8D 6.52 4 Ⅴ 10 1/8D 7.05 12 Ⅰ 10 0 6.56 4 Ⅲ 0 2/8D 7.4 18 Ⅴ 10 2/8D 7.87 25 Ⅰ 10 0 6.56 4 Ⅲ 0 3/8D 8.51 36 Ⅴ 10 3/8D 8.67 38 Ⅰ 10 0 6.56 4 Ⅲ 0 4/8D 9.02 44 Ⅴ 10 4/8D 9.56 52 Ⅰ 20 0 7.6 21 Ⅲ 0 1/8D 6.52 4 Ⅴ 20 1/8D 7.71 23 Ⅰ 20 0 7.6 21 Ⅲ 0 2/8D 7.4 18 Ⅴ 20 2/8D 8.44 34 Ⅰ 20 0 7.6 21 Ⅲ 0 3/8D 8.51 36 Ⅴ 20 3/8D 9.21 47 Ⅰ 20 0 7.6 21 Ⅲ 0 4/8D 9.02 44 Ⅴ 20 4/8D 9.92 58 Ⅰ 30 0 7.47 19 Ⅲ 0 1/8D 6.52 4 Ⅴ 30 1/8D 7.86 25 Ⅰ 30 0 7.47 19 Ⅲ 0 2/8D 7.4 18 Ⅴ 30 2/8D 8.55 36 Ⅰ 30 0 7.47 19 Ⅲ 0 3/8D 8.51 36 Ⅴ 30 3/8D 9.17 46 Ⅰ 30 0 7.47 19 Ⅲ 0 4/8D 9.02 44 Ⅴ 30 4/8D 9.24 47 Ⅰ 40 0 7.35 17 Ⅲ 0 1/8D 6.52 4 Ⅴ 40 1/8D 7.63 21 Ⅰ 40 0 7.35 17 Ⅲ 0 2/8D 7.4 18 Ⅴ 40 2/8D 7.81 24 Ⅰ 40 0 7.35 17 Ⅲ 0 3/8D 8.51 36 Ⅴ 40 3/8D 8.06 28 Ⅰ 40 0 7.35 17 Ⅲ 0 4/8D 9.02 44 Ⅴ 40 4/8D 8.28 32
下载: 导出CSV
表 10 不同ΔH与Δy工况组合时，双风力发电机整体功率及功率提升比变化情况
Tab. 10. The variation of overall power and power augmentation rate for dual wind turbine under various ΔH and Δy cases
工况 ΔH Δy 功率
/MW功率
提升比/%Ⅱ −3/20D 0 6.58 5 Ⅲ 0 1/8D 6.52 4 Ⅵ −3/20D 1/8D 6.79 8 Ⅱ −3/20D 0 6.58 5 Ⅲ 0 2/8D 7.4 18 Ⅵ −3/20D 2/8D 7.48 19 Ⅱ −3/20D 0 6.58 5 Ⅲ 0 3/8D 8.51 36 Ⅵ −3/20D 3/8D 8.14 30 Ⅱ −3/20D 0 6.58 5 Ⅲ 0 4/8D 9.02 44 Ⅵ −3/20D 4/8D 8.91 42 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 1/8D 6.52 4 Ⅵ −6/20D 1/8D 7.37 17 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 2/8D 7.4 18 Ⅵ −6/20D 2/8D 7.87 25 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 3/8D 8.51 36 Ⅵ −6/20D 3/8D 8.53 36 Ⅱ −6/20D 0 7.48 7 Ⅲ 0 4/8D 9.02 44 Ⅵ −6/20D 4/8D 9.15 46 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 1/8D 6.52 4 Ⅵ −9/20D 1/8D 8.3 32 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 2/8D 7.4 18 Ⅵ −9/20D 2/8D 8.62 37 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 3/8D 8.51 36 Ⅵ −9/20D 3/8D 9.06 44 Ⅱ −9/20D 0 8.31 8 Ⅲ 0 4/8D 9.02 44 Ⅵ −9/20D 4/8D 9.6 53
下载: 导出CSV
广 告 封面图片：具身智能，御风驭光 ——“AI+气象”赋能“气候韧性新型能源体系”----------- 封一 华能汕头勒门（二）海上风电项目---------------------------------------------------------------------- 封二 广西防城港海上风电示范项目---------------------------------------------------------------------------- 封三 中国能源建设集团广东省电力设计研究院有限公司------------------------------------------------ 封四
下载: 导出CSV
-
[1] VERMEER L J, SØRENSEN J N, CRESPO A. Wind turbine wake aerodynamics [J]. Progress in aerospace sciences, 2003, 39(6/7): 467-510. DOI: 10.1016/s0376-0421(03)00078-2. [2] 罗莎莎, 郭经韬, 蔡颖倩, 等. 面向碳中和的广东省电源结构转型分析 [J]. 南方能源建设, 2024, 11(4): 102-110. DOI: 10.16516/j.ceec.2024.4.10. LUO S S, GUO J T, CAI Y Q, et al. Analysis on power supply structure transformation towards carbon neutrality in Guangdong [J]. Southern energy construction, 2024, 11(4): 102-110. DOI: 10.16516/j.ceec.2024.4.10. [3] ROGA S, BARDHAN S, KUMAR Y, et al. Recent technology and challenges of wind energy generation: a review [J]. Sustainable energy technologies and assessments, 2022, 52: 102239. DOI: 10.1016/j.seta.2022.102239. [4] 李胜, 葛文澎, 吴嘉诚, 等. 风力机组尾流模型适用性评价 [J]. 南方能源建设, 2024, 11(1): 42-53. DOI: 10.16516/j.ceec.2024.1.05. LI S, GE W P, WU J C, et al. Applicability evaluation of wind turbine wake models [J]. Southern energy construction, 2024, 11(1): 42-53. DOI: 10.16516/j.ceec.2024.1.05. [5] 李东东, 张先明, 姚寅, 等. 计及转子动能损失和风速相关性的风电场有效惯量估计 [J]. 电力系统保护与控制, 2023, 51(22): 63-73. DOI: 10.19783/j.cnki.pspc.230187. LI D D, ZHANG X M, YAO Y, et al. Estimation of effective inertia of a wind farm considering rotor kinetic energy loss and wind velocity correlation [J]. Power system protection and control, 2023, 51(22): 63-73. DOI: 10.19783/j.cnki.pspc.230187. [6] ALFREDSSON P H, DAHLBERG J A. Measurements of wake interaction effects on the power output from small wind turbine models [R]. Stockholm: FFA, 1981. [7] VERMEULEN P E J, BUILTJES P J H. Turbulence measurements in simulated wind-turbine clusters [R]. The Hague, Netherlands: Netherlands Organization for Applied Scientific Research, 1982. [8] VERMEULEN P E J. An experimental analysis of wind turbine wakes [C]//British Hydromechanics Research Association (BHRA), Proceedings of the 3rd International Symposium on Wind Energy Systems. Lyngby, Denmark: BHRA, 1980: 431-450. [9] KROGSTAD P Å, ERIKSEN P E. "Blind test" calculations of the performance and wake development for a model wind turbine [J]. Renewable energy, 2013, 50: 325-333. DOI: 10.1016/j.renene.2012.06.044. [10] BARTL J, SÆTRAN L. Blind test comparison of the performance and wake flow between two in-line wind turbines exposed to different turbulent inflow conditions [J]. Wind energy science, 2017, 2(1): 55-76. DOI: 10.5194/wes-2-55-2017. [11] PIERELLA F, KROGSTAD P Å, SÆTRAN L. Blind Test 2 calculations for two in-line model wind turbines where the downstream turbine operates at various rotational speeds [J]. Renewable energy, 2014, 70: 62-77. DOI: 10.1016/j.renene.2014.03.034. [12] KROGSTAD P Å, SÆTRAN L, ADARAMOLA M S. "Blind Test 3" calculations of the performance and wake development behind two in-line and offset model wind turbines [J]. Journal of fluids and structures, 2015, 52: 65-80. DOI: 10.1016/j.jfluidstructs.2014.10.002. [13] 郭静婷. 风电场中风力机间相互影响的研究 [D]. 呼和浩特: 内蒙古工业大学, 2010. GUO J T. Research on optimization collocation in wind farm [D]. Hohhot: Inner Mongolia University of Technology, 2010. [14] WHALE J, ANDERSON C G, BAREISS R, et al. An experimental and numerical study of the vortex structure in the wake of a wind turbine [J]. Journal of wind engineering and industrial aerodynamics, 2000, 84(1): 1-21. DOI: 10.1016/S0167-6105(98)00201-3. [15] 郭茂丰, 张立茹, 李得银, 等. 偏航状态下水平轴风力机尾迹偏移及湍流特征分析 [J]. 排灌机械工程学报, 2020, 38(7): 702-707. DOI: 10.3969/j.issn.1674-8530.18.0273. GUO M F, ZHANG L R, LI D Y, et al. Analysis on wake deviation and turbulence characteristics of horizontal-axis wind turbine under yawed condition [J]. Journal of drainage and irrigation machinery engineering, 2020, 38(7): 702-707. DOI: 10.3969/j.issn.1674-8530.18.0273. [16] FLETCHER T M, BROWN R E. Simulation of wind turbine wake interaction using the vorticity transport model [J]. Wind energy, 2010, 13(7): 587-602. DOI: 10.1002/WE.379. [17] ZHANG W G, WANG Y Y, SHEN Y Z, et al. CFD studies of wake characteristics and power capture of wind turbines with trailing edge flaps [J]. IEEE access, 2020, 8: 7349-7361. DOI: 10.1109/ACCESS.2020.2964620. [18] LIU Y C, XIAO Q, INCECILK A, et al. Establishing a fully coupled CFD analysis tool for floating offshore wind turbines [J]. Renewable energy, 2017(112): 280-301. DOI: 10.1016/j.renene.2017.04.052. [19] JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development [R]. Golden: National Renewable Energy Lab. (NREL), 2009. DOI: 10.2172/947422. [20] WEN B R, TIAN X L, DONG X J, et al. Influences of surge motion on the power and thrust characteristics of an offshore floating wind turbine [J]. Energy, 2017, 141: 2054-2068. DOI: 10.1016/j.energy.2017.11.090. [21] MICALLEF D, SANT T. Loading effects on floating offshore horizontal axis wind turbines in surge motion [J]. Renewable energy, 2015, 83: 737-748. DOI: 10.1016/j.renene.2015.05.016. [22] TU Y, ZHANG K, HAN Z L, et al. Aerodynamic characterization of two tandem wind turbines under yaw misalignment control using actuator line model [J]. Ocean engineering, 2023, 281: 114992. DOI: 10.1016/j.oceaneng.2023.114992. [23] NAKHCHI M E, WIN NAUNG S, RAHMATI M. A novel hybrid control strategy of wind turbine wakes in tandem configuration to improve power production [J]. Energy conversion and management, 2022, 260: 115575. DOI: 10.1016/j.enconman.2022.115575. [24] MIAO W P, LI C, PAVESI G, et al. Investigation of wake characteristics of a yawed HAWT and its impacts on the inline downstream wind turbine using unsteady CFD [J]. Journal of wind engineering and industrial aerodynamics, 2017, 168: 60-71. DOI: 10.1016/j.jweia.2017.05.002. -
计量
- 文章访问数: 69
- HTML全文浏览量: 41
- PDF下载量: 3
- 被引次数: 0
