上海地区输电线路走廊稀缺，因此输电导线换向、支接多采用换向分支钢管杆结构。换向分支杆高度高，横担相互垂直布置导致风荷载作用下结构受力复杂。此外横担和主杆均采用沿长度方向截面变化的正多边形钢管，结构建模难度较大。针对强风作用下换向分支杆的结构响应分析还未开展。

电力系统在自然灾害下的损失严重^[1-4]。而输电线路分布广泛，强风作用下输电塔倒塔事故频繁发生。目前针对输电线路的研究大多聚焦于钢管塔和角钢塔，如输电塔抗风能力的实用评估^[5-7]，强风下的倒塌分析^[8-10]以及风致结构响应分析^[11-14]。相应的输电塔建模大部分采用梁单元有限元模型，例如杨风利等^[15]建立了500 kV大跨越钢管塔模型并提出了风振系数的计算方法；张丽娟^[16]等利用1 MV钢管塔梁单元模型进行倒塌破坏模拟，并用真型倒塌破坏试验验证了模型的有效性；邓洪洲^[17]等人对钢管塔建立多尺度有限元模型，整塔采用梁单元，塔脚采用壳单元，分析了塔脚节点的承载力。而对于沿长度方向截面变化的正多边形钢管组成的换向分支杆相应的建模方法和风振响应分析较少，有必要获得可用于进行风振响应计算的有限元模型，并在此基础上对其风振响应和薄弱位置进行分析，为换向分支杆工程设计和应用提供参考。

文章以上海地区某110 kV典型换向分支钢管杆塔结构为研究对象，通过建立壳单元有限元模型得到其真实的模态，并提出简化的梁单元有限元模型，对比模态和频率验证其有效性。通过不同风向角下的动力特性和响应分析，研究不同风向角下换向分支杆的风振响应，得到不同风向角下的薄弱位置以及设计控制因素，为上海地区输电线路结构的工程设计提供参考。

本文中的典型换向分支杆取自上海某110 kV输电线路，主要设计参数如下：

（1）电压等级：110 kV；

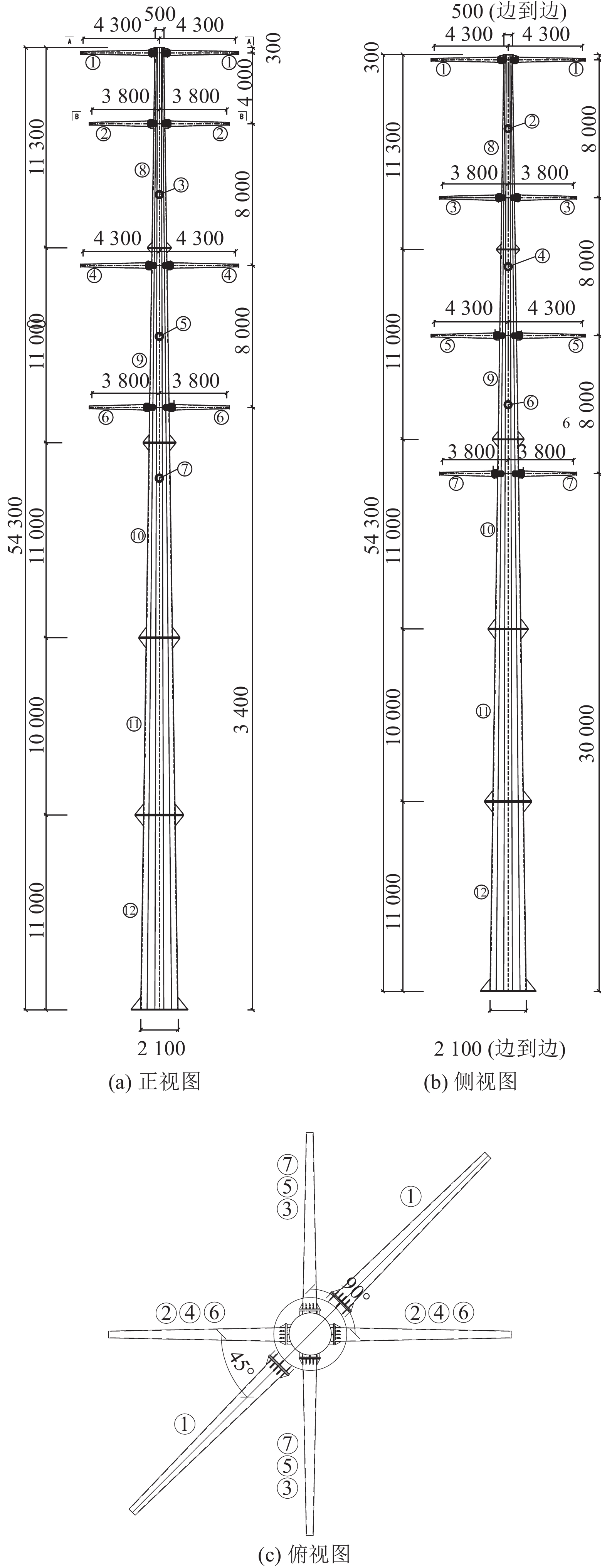
（2）该输电塔总高：54.3 m；呼高：30 m；根开：2.1 m；

（3）回路数：三回路；

（4）导地线型号：

地线：JLB20A-100-FJ，自重0.6767 kg/m，直径15.20 mm，截面积121.1 mm²，弹性模量153900 MPa，破断张力135200 N，年平均运行张力比为0.16；

导线：JL3/G1A-240/30，自重0.9215 kg/m，直径21.60 mm，截面积276.00 mm²，弹性系数70500 MPa，破断张力75190 N，年平均运行张力比为0.167，为2分裂导线。

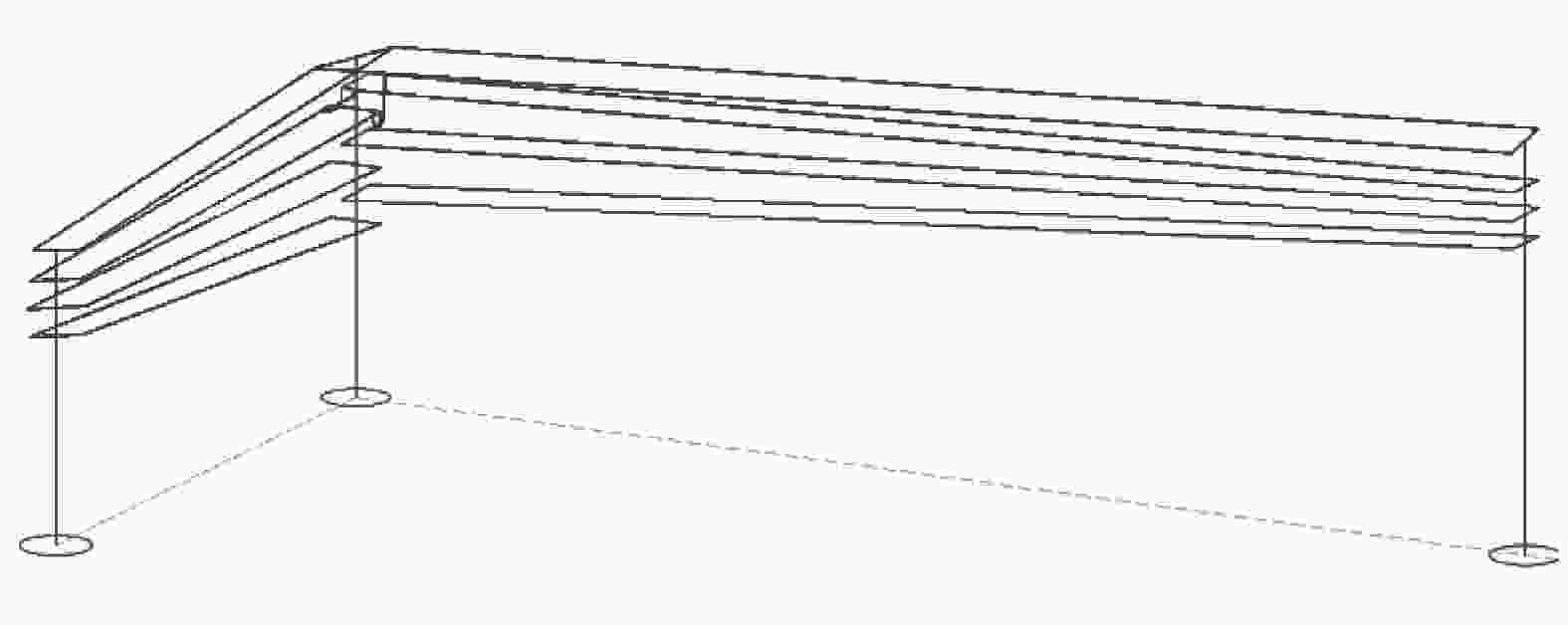
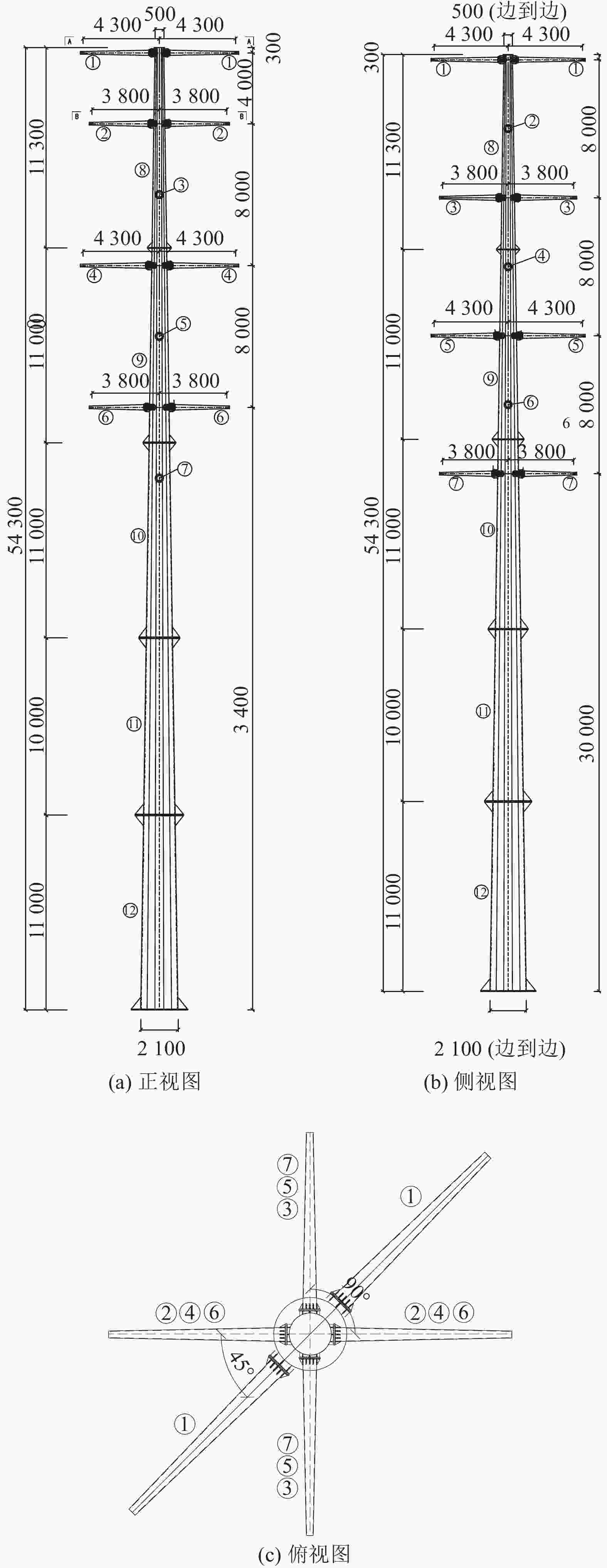
该典型换向分支杆塔体采用正十六边形方管，基础处方管边对边距离为2100 mm，顶部方管边对边的距离为500 mm。杆塔总高54.3m，如图1所示。

图  1  典型换向分支杆设计信息

Figure 1.  Design information of typical diverging branch rod

塔体各分段截面和材料性质以及详细的横担截面参数信息和材料信息如表1所示。7组横担包括1组地线横担和6组导线横担，其中地线横担为45°方向，②④⑥3组导线横担为0°方向，③⑤⑦3组导线横担为90°方向。

该换向分支杆的转向设计及导地线布置如图2所示，设计档距分别为前档距180 m和后档距90 m，线路转角为90°，最大设计风速为29 m/s。

图  2  换向分支杆线路信息示意图

Figure 2.  Information of the line with diverging branch rod

本文有限元分析采用ABAQUS软件，换向分支杆模型的材料本构关系采用理想弹塑性模型，在满足足够计算精度的要求下提高计算效率。所研究输电塔为钢管塔，构件由钢管构成，杆件长度方向尺寸远大于其他2个方向尺寸，可以选用壳单元计算沿构件长度方向的应力变化，因此选用shell188壳单元考虑沿长度方向截面尺寸的改变。单元质量恒定且连续。构件根据长度的不同划分为多个单元。每个单元两端节点有3个方向平动和3个方向转动自由度，应力梯度计算方法为二次插值方法。输电塔杆塔的壳单元有限元模型如图3所示。

图  3  换向分支杆壳单元有限元模型

Figure 3.  Finite element model of diverging branch rod

塔身结构的边界条件为通过嵌固方式（Encastre）约束塔腿节点，符合实际工程中输电塔结构与混凝土基础共同浇筑以及与高强螺栓的连接方式。此外，建模的过程中由于换向分支杆塔身不同塔段之间以及塔身和横担之间均采用法兰连接，可以视为固结，因此在节点处理上模型中的节点均设置为固结。杆塔总质量为62765.8 kg，分割有限元单元总数为37229，节点总数为37977。

模态分析是研究结构的动态特性、振动分析和动态优化的常用方法。文中对换向分支杆进行模态分析， 如表2所示，该典型换向分支杆的模态主要以弯曲模态为主，由于导线横担的对称布置以及地线横担布置在45°方向，结构的前四阶模态以对称轴方向的一阶和二阶弯曲为主，其中一阶弯曲的频率在0.80～0.81 Hz附近，更容易发生一阶弯曲。

换向分支杆壳单元模型在网格划分后单元数目较多，进行动力分析时存在着计算时间长、计算效率低的问题。而梁单元模型早已被证明可以用于输电线路的建模，但针对换向分支杆的特点需要解决2个问题：（1）附加钢管以及法兰的重量；（2）如何采用梁单元模拟变截面的正多边形钢管。

首先考虑到同一横担的附加钢管基本在同一高度处，而风振系数则主要随高度进行变化。本研究将附加钢管的重量简化到横担上，杆身法兰及法兰加劲板等附属连接装备采用与附加钢管同样的方法进行简化，通过改变横担的材料密度，将附加钢管的质量平均分配，使结构动力特性保持一致。然后针对变截面钢管采用多段模拟的形式进行处理，如54.3 m的塔身部位按1 m分段，共分成55段，每段的截面取其平均高度处对应的钢管截面，而横担则按0.5 m分段，截面的取法与塔身钢管一致。选用B31梁单元进行建模，简化梁单元有限元模型如图4所示。

图  4  换向分支杆简化梁单元有限元模型

Figure 4.  Finite element model of diverging branch rod with beam elements

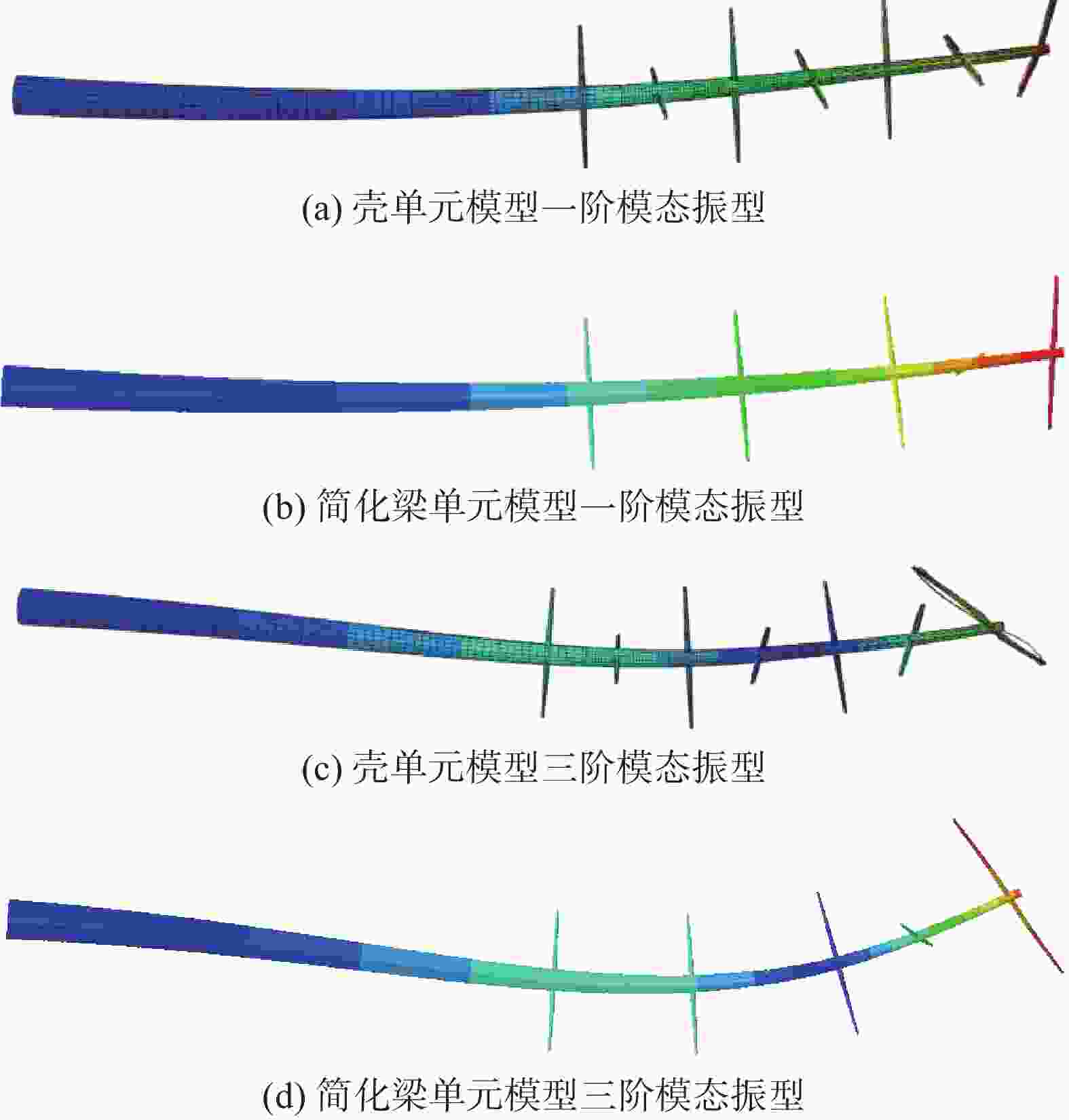
对简化梁单元进行模态分析，与壳单元模态分析的频率对比结果如表2所示，一阶和三阶模态形状的云图对比如图5所示。简化模型前四阶模态的最大误差为0.87%，可以忽略。而结构的一阶振型与壳单元模型一致，均为45°方向的半波弯曲。而三阶振型均为45°方向的S形的二阶弯曲。从振动模态和振动频率的角度，可以看出简化梁单元模型可准确反映换向分支杆的动力特性，可以用于后续的动力响应分析。

图  5  简化模型一阶和三阶模态振型对比

Figure 5.  Comparison of the first and third-order mode shape of the simplified model

考虑到上海地区强风大多为台风导致，而相关研究认为用对数律描述平均风剖面规律与台风实际观测结果更加吻合^[18-19]，因此本文采用对数律描述输电塔中各节点的风速时程曲线，其表达式为：

式中：

$ \kappa $ ——Von Karman常数，一般取为0.4；

$ {{\textit z}_0} $ ——地面粗糙长度（m），根据不同地貌取不同值，但一般大于地面障碍物高度1/10，其物理含义为风速等于0的高度；

$ {u_*} $——剪切波速（m/s），反映地面障碍物对气流的摩阻效应，其值可根据标准高度$ {{\textit z}_{\mathrm{r}}} $及该处的平均风速$ {\overline U _{\mathrm{r}}} $计算。

脉动风是由气流中的湍流产生的，所以在计算分析所关注的时间段内可以认为脉动风是基于平均风的平稳各态历经随机过程，其均值为0。本文选用Kaimal谱作为后续随机风场模拟的基础风谱。因为换向分支杆的高度为54.3 m，需要考虑高度对风场能量分布的影响，而Kaimal谱的自变量中考虑了高度，其表达式如下所示

式中：

n ——涡旋的自然频率（Hz）；

W(z) ——z高度处的平均风速（m/s）。

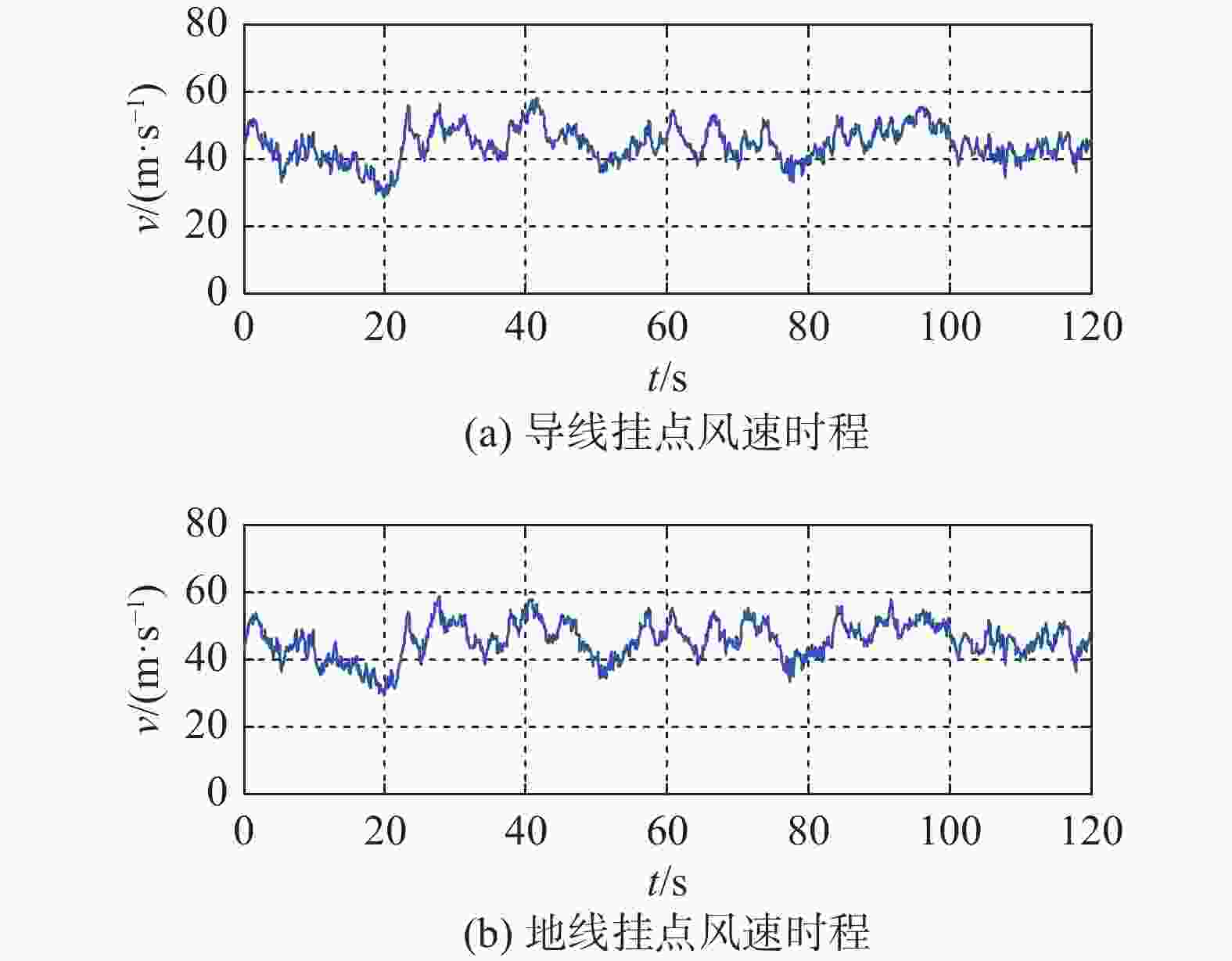
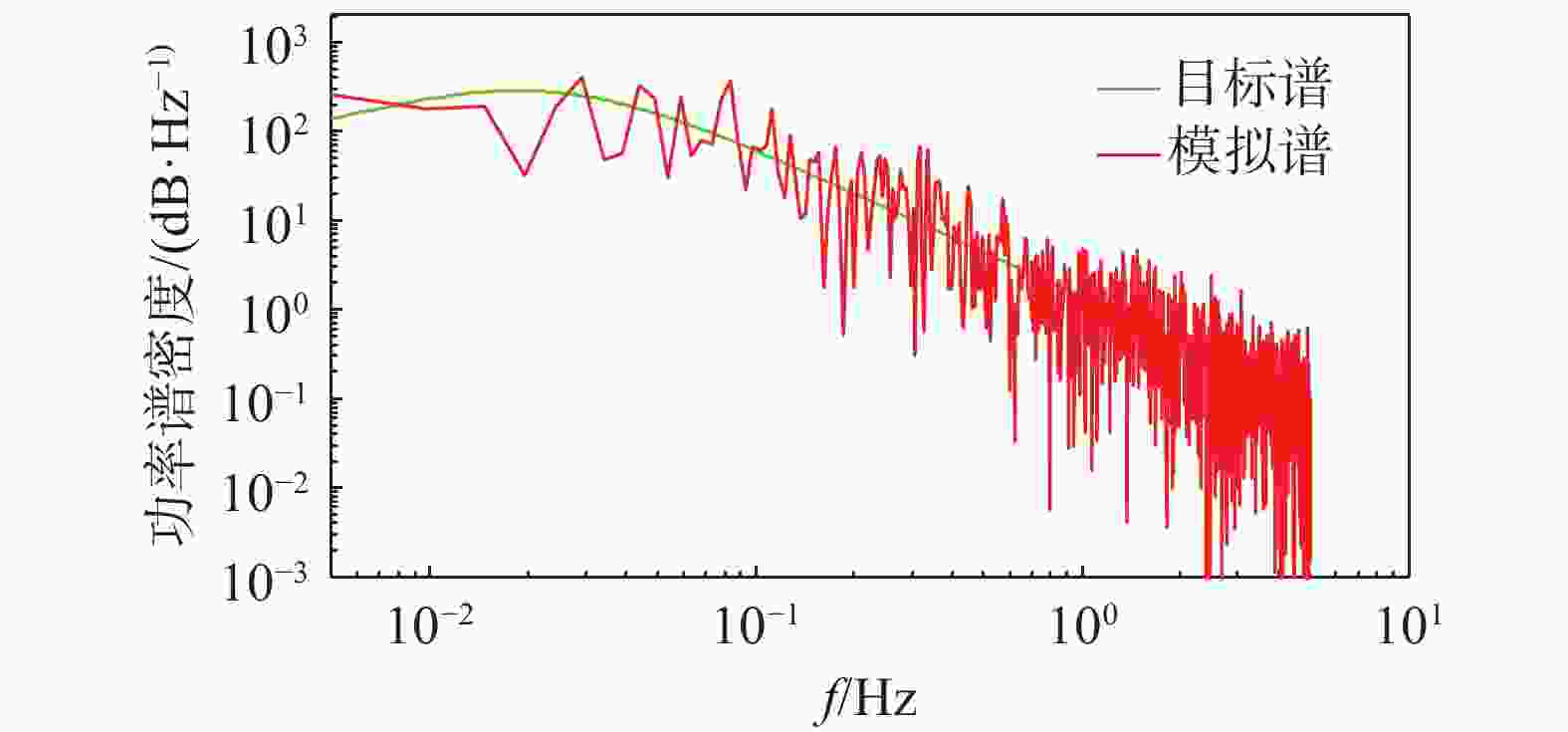
在随机傅里叶谱^[20]的基础上，模拟换向分支杆的随机风场，场地类别为B类，地面粗糙长度为0.05 m。换向分支杆分为12个塔段或组件，每个塔段或组件计算中点位置处的脉动风速。导、地线则以挂点处计算脉动风速。取采样频率为10 Hz，即dt=0.1 s，总时长为120 s。以29 m/s基本风速为例，得到的导、地线挂线点风速时程如图6所示。对应的功率谱如图7所示。

图  6  导、地线风速时程图

Figure 6.  Wind speed time history diagram for conductor and ground lines

图  7  换向分支杆顶功率谱

Figure 7.  Power spectral density at the top of the diverging branch rod

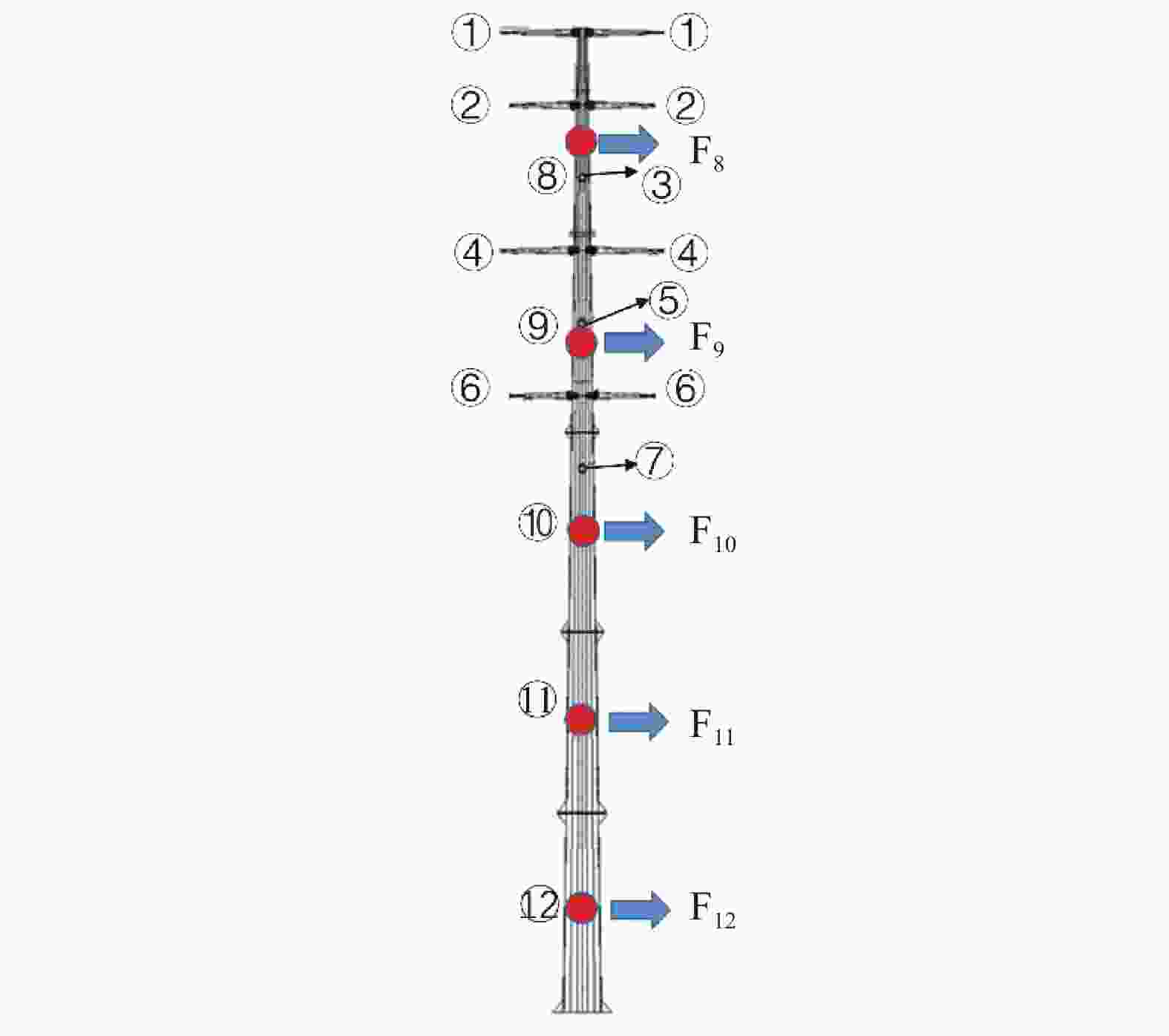
在得到风速时程后按规范^[21]规定将风荷载施加到换向分支杆节点上。风荷载激励均采用集中力施加的方式。每段的动力风荷载通过第3.1节动力风场模拟中的理论计算后以集中力的形式施加到塔段的中间节点上。因为模型采用简化梁单元，每个塔段被简化为不同截面的梁单元的直线，对塔段中部位置的梁单元进行打断，将风荷载施加到这个位置，如图8所示。其次，针对导线和绝缘子串荷载，其施加方式与塔身风荷载类似，将导线和绝缘子串荷载通过动力风场模拟获得后以集中力的形式施加到挂线点处，风荷载施加方向为垂直横担方向，重力荷载的施加方向为竖直向下。针对不同风攻角下风荷载的分配原则，本文参考《架空输电线路荷载规范》（GB5154－2018）^[21]中表4.2.10（角度风吹时风荷载分配表）进行分配。

图  8  塔身风荷载施加位置

Figure 8.  Applied location of wind load in the tower

在风荷载作用下，输电塔的位移响应可以通过功率谱分析，识别出其主要振动频率及对应的能量峰值。90°风向角下的响应功率谱如图9所示。在输电塔的位移功率谱中，第一个高幅值频率为0.81 Hz，对应的幅值为0.48，说明在该频率下，结构的振动响应最为显著。这一现象可以解释为输电塔在风荷载作用下，主要的振动模式集中在一阶和二阶振型，这与结构的固有频率相匹配。第二个高幅值频率的频率为2.64 Hz，对应的幅值为0.016。这表明在该频率下，结构的振动响应相对较小，对应为三阶和四阶振型。尽管三阶和四阶振型的存在对整体结构的动态响应有一定影响，但其能量贡献相对较小。

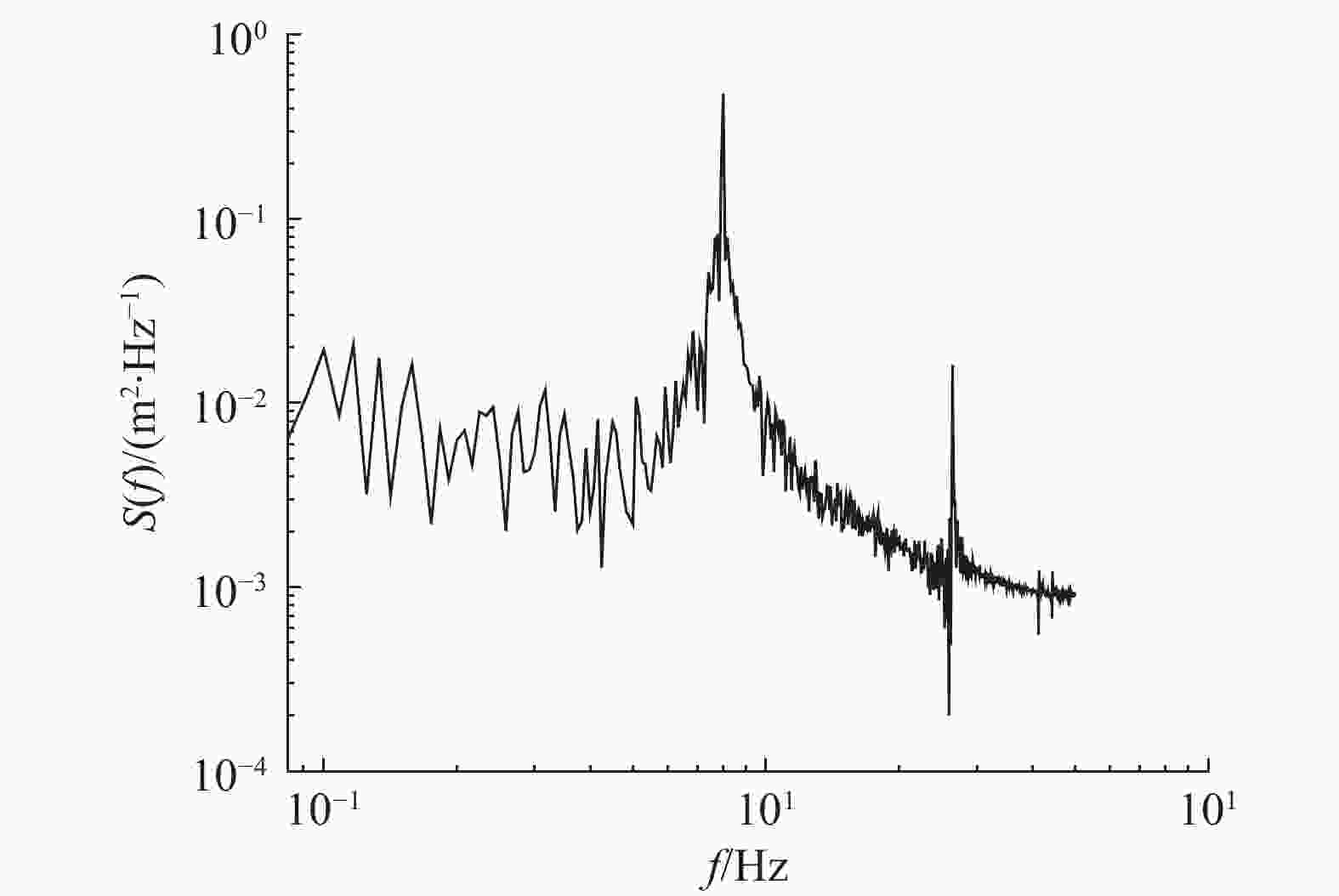
图  9  塔身顶点顺风向位移功率谱

Figure 9.  Power spectral density at the top of the diverging branch rod along the wind direction

塔身顶点顺风向位移响应如图10所示，可以看出塔顶节点的位移随风荷载脉动，其均值为0.405 m，最大位移响应为1.184 m。横担端点的位移响应和塔顶节点基本相同，这说明90°风向角下地线横担并没有明显的扭转响应，且风荷载作用下横担的变形也较小，位移响应主要由顺风向弯曲控制，这与功率谱中第一峰值的位置对应弯曲变形一致。

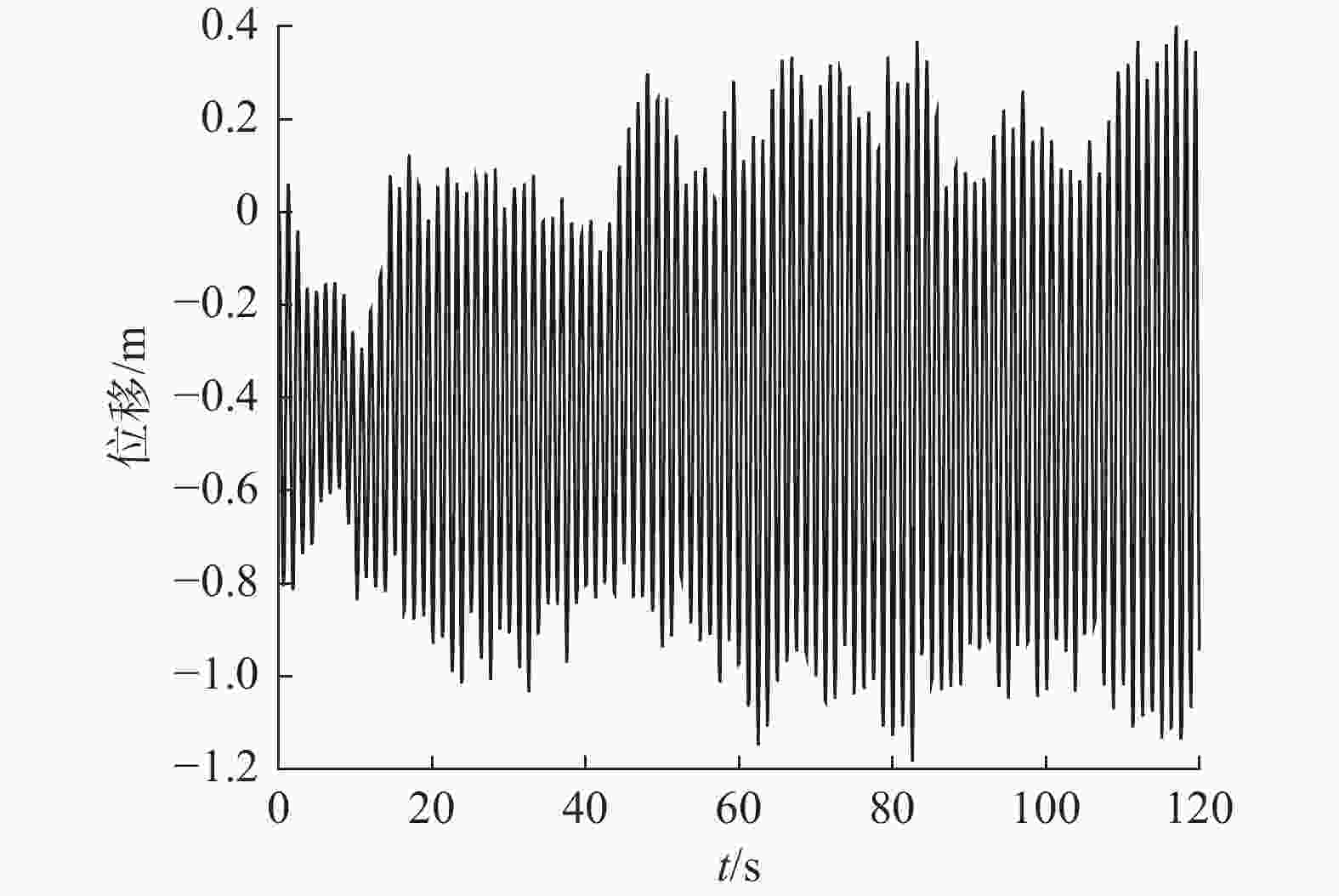
图  10  90°风向角下塔身顶点顺风向位移响应

Figure 10.  Power spectral density at the top of the diverging branch rod perpendicular to the wind direction

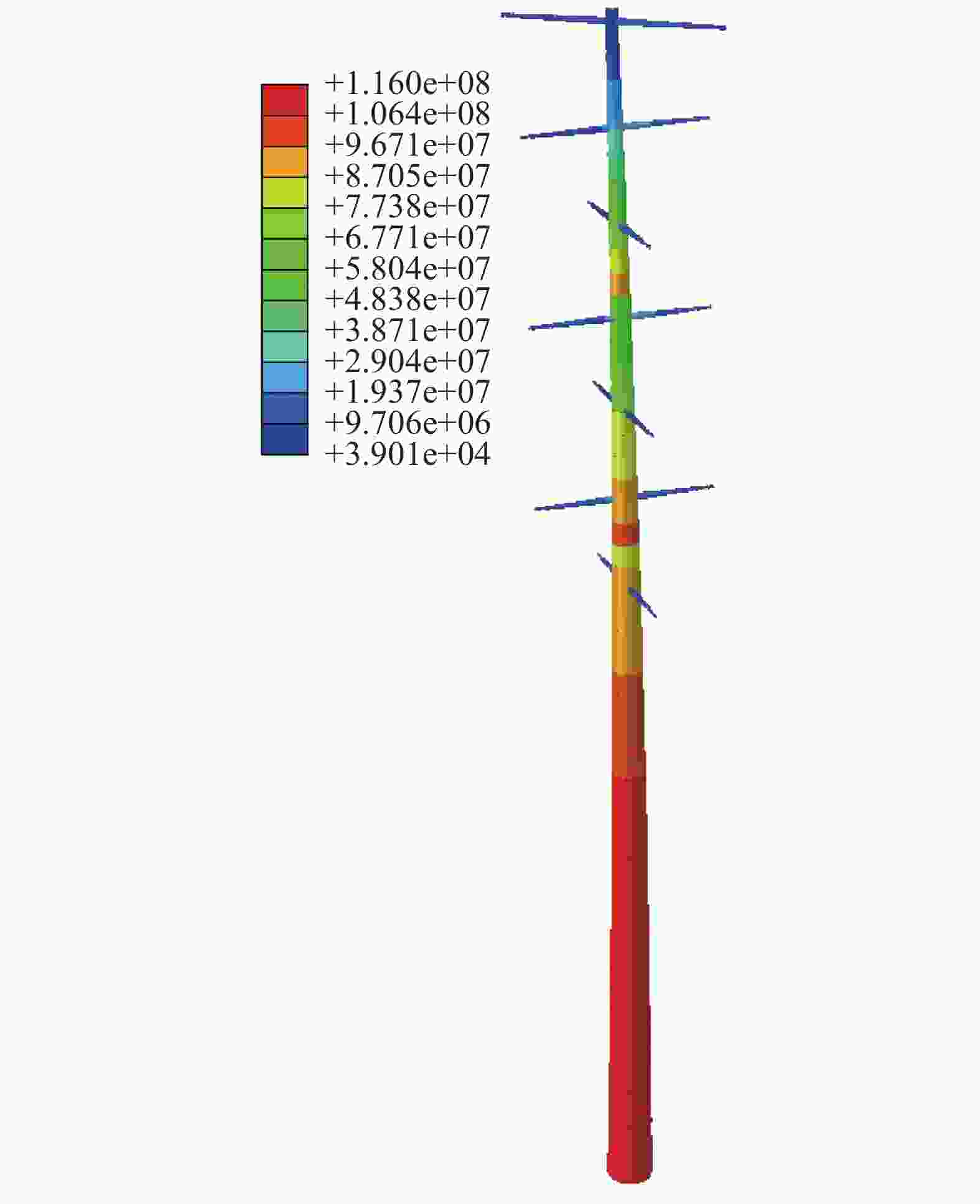
选取90°风向角下塔顶位移最大时刻，其Mises应力分布情况如图11所示，从图中可以看出90°风向角下，应力响应最大的位置在塔身底部，其最大应力为116.00 MPa。

图  11  90°风向角下换向分支杆Mises应力图

Figure 11.  Mises stress of the diverging branch rod under the wind perpendicular to the wind direction

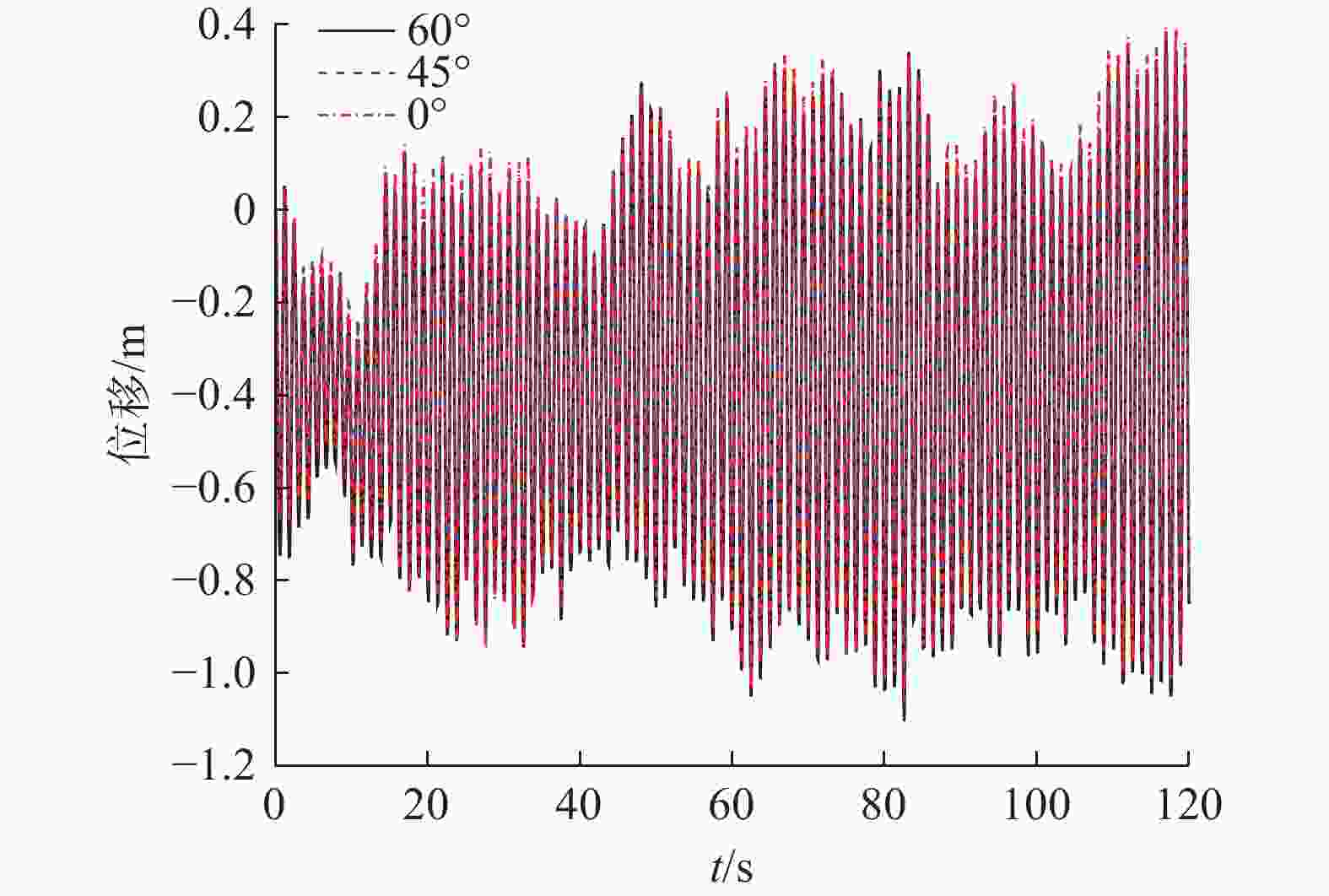
60°、45°和0°风向角下塔身顶点的位移响应如图12所示，可以看出不同风向角下振动响应均相似，响应趋势与风向角无关。最大位移随着风向角靠近45°逐渐减小，而60°对应的最大位移则明显大于0°。不同风向角下的结构Mises应力图如图13所示，可以看出45°风向角下的应力响应最大，60°风向角次之，0°风向角最小。

图  12  3种风向角下塔身顶点位移响应对比

Figure 12.  The displacements at the top of rod under three different wind directions

图  13  3种风向角下换向分支杆Mises应力对比图

Figure 13.  The Mises stresses of the rod under three different wind directions

通过对换向分支杆风振响应的研究，可以全面了解换向分支杆在不同风向角下的动力响应特征，确定结构的薄弱位置，并提出相应的设计优化和加固建议。这对于提升输电塔的抗风能力，确保其在强风作用下的安全稳定运行具有重要意义。

如图14所示，在不同风向下，输电塔的最大风振位移表现出显著差异：在90°风向下塔顶最大位移最大，为1.164 m，60°风向下次之为1.079 m，0°风向下为1.047 m，45°风向下最小为0.868 m。这表明从最大塔顶位移看，90°风攻角为塔顶位移最危险的角度。随着风攻角减小到45°，塔顶位移逐渐减小；而风攻角从45°减小到0°，塔顶位移则逐渐增大。此现象反映了导线的风荷载作用引起了塔顶位移的变化，由于两侧档距的差距，90°风攻角下的位移响应明显大于0°风攻角下的位移响应，而斜向风即45°风攻角下导线的荷载相比最低，因此塔顶位移最小。

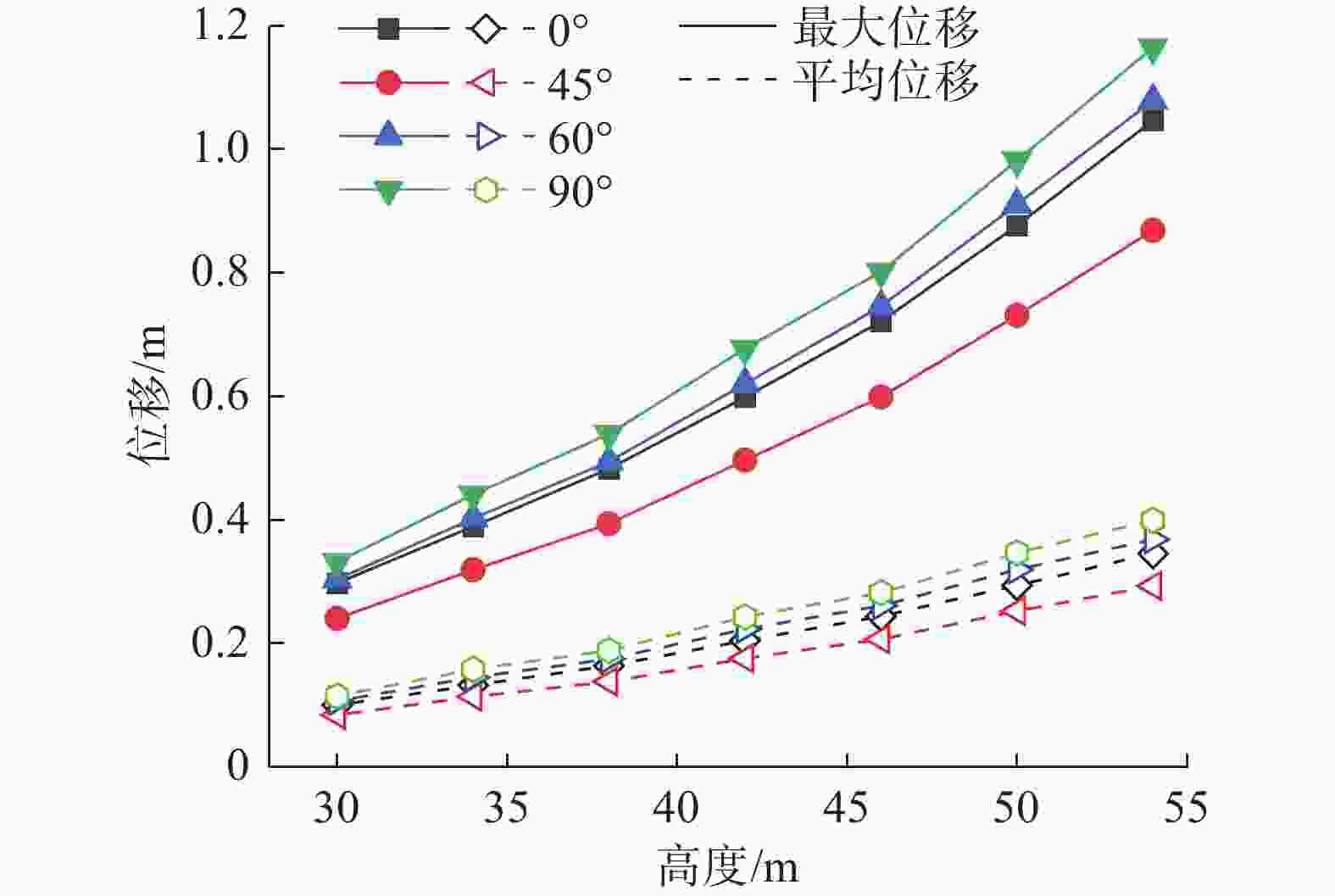
图  14  不同风向角下顶部位移响应对比

Figure 14.  Comparison of displacements at the top of the rods at different wind angles

对于平均风振位移的影响，在不同风向下，输电塔的平均风振位移表现出一定差异。90°风攻角下平均位移为0.399 m，而随着风向角度的减小，塔顶平均位移减小到0.368 m（60°风攻角）及0.293 m（45°风攻角），而风攻角从45°减小到0°，位移增大到0.346 m。从平均位移的角度看，其变化趋势和塔顶最大位移相似，说明风场中平均风和脉动风的作用效果在不同风攻角下基本相同。结构的平均位移与导线的荷载直接相关，因此90°风攻角为塔顶位移最危险的风向角。

通过对比不同风向下的最大风振位移和平均风振位移，分析不同风向下的风振特性，可以看出90°横向风影响最大。这是由于横向风直接作用于塔的侧面和档距较大的导地线，产生较大的风压，导致更大的振动。倾斜风如60°和45°次之，60°风向下的振动位移次高，表明倾斜风（接近横向）对塔的影响也较大。45°风向下的振动位移最低，是因为该风向下导地线的风荷载最小。0°风攻角下的影响仅大于45°，这是因为0°风攻角作用下导地线的档距远远低于90°时的档距，因此风振响应较小。

不同风向角下换向分支杆的应力和位移如表3所示，可以看出0°风向角对应顺风方向，风力直接作用在塔的正面。虽然最大应力较低，但最大塔顶位移较大，说明在正面风力作用下，整体位移较明显。应力较低则是因为风的方向和不平衡张力作用方向相反，作用力进行部分抵消，降低了根部应力。45°风向角对应斜风方向，风力同时作用在塔的侧面和正面。最大应力显著增大，发生在塔身根部，表明斜风对塔身的应力集中效应明显。60°风向角对应较大的斜风方向，最大应力较45°有所减少，但仍较高，发生在塔身根部。此风向角下最大塔顶位移有所增加，表明此角度下塔顶振动显著。90°风向角对应横风方向，最大应力最高，发生在塔身根部，表明横风对塔身的应力影响最为显著，此时最大塔顶位移也最大，表明横风引起的整体振动最剧烈。

对比不同风向角下的最大应力和对应部位可以发现，在0°风向角下最大应力为22.41 MPa，出现在地线横担根部。而在45°、60°和90°风向角下最大应力分别为86.69 MPa、54.32 MPa和116.00 MPa，出现在塔身根部。这说明从应力的角度上看，塔身根部相较于其他部位更危险。对于塔身根部的应力，由于工程设计允许的最大应力110.00 MPa，90°风攻角下其实际应力已经超过了设计允许应力，而其他风攻角下均未超过工程设计中该段允许最大应力。因此，90°风攻角为结构应力响应最大的角度。

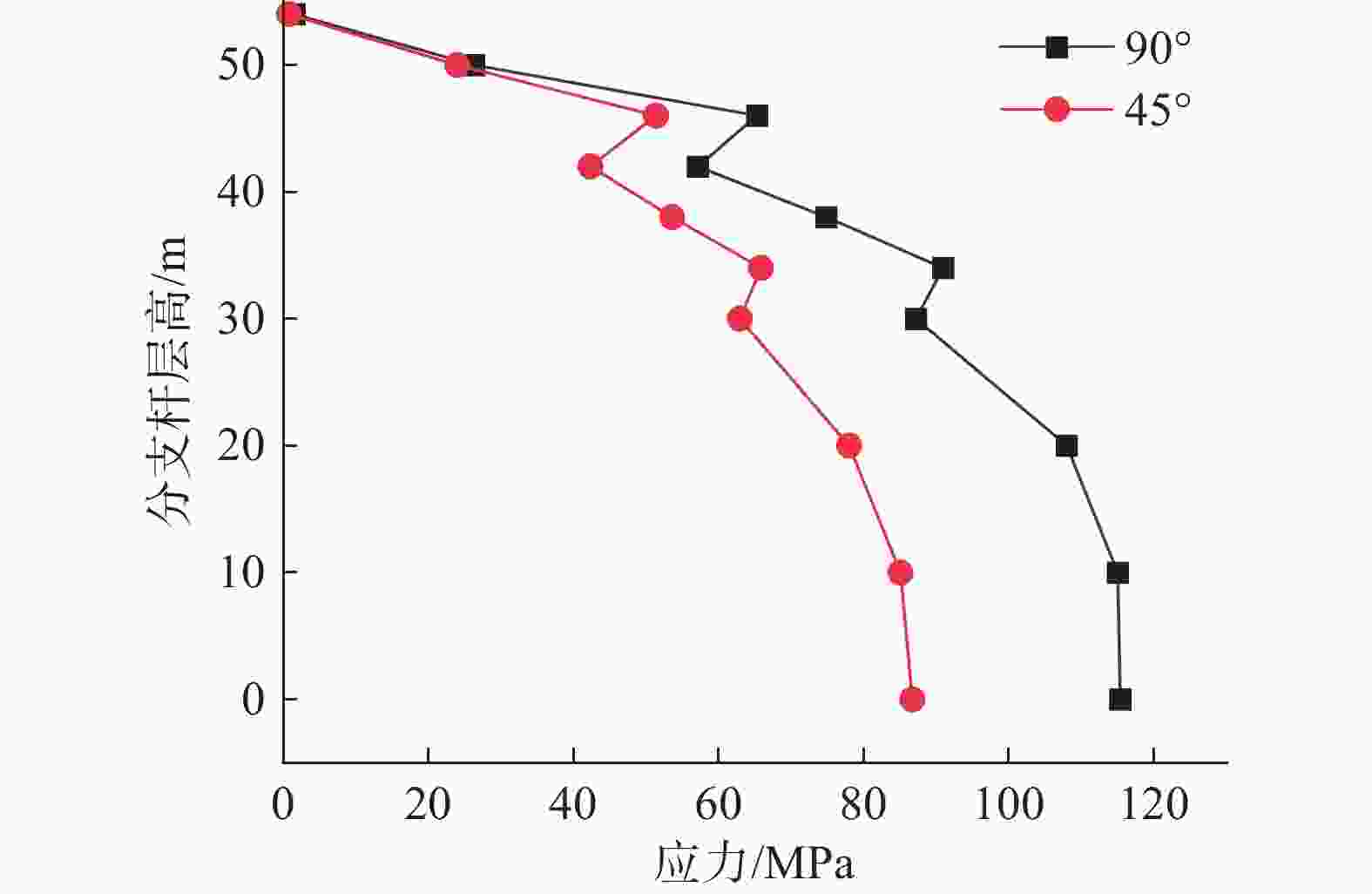
通过对比不同风向角下的最大和平均塔顶位移，可以得出以下结论：随着风向逐渐从垂线路方向（0°和90°）过渡到斜向风方向，塔顶的最大位移和平均风振位移均会减小。由于90°方向对应的线路档距（180 m）大于0°方向对应的线路档距（90 m），所以最大位移较高。根据《高耸结构设计规定》，对于以风荷载为主的荷载标准组合作用下，其水平位移角限值为1/50，而该典型换向分支杆的总高为54.3 m,对应的水平位移值为1.086 m，本文90°风向角下换向分支杆顶部位移超过限值，塔顶位移应为其设计中的控制因素。在实际工程应用中，针对已建设的换向分支杆可以考虑采用一定的加固措施来减小最大塔顶位移；而针对计划建设的换向分支杆，可以考虑减小档距或增大截面来避免最大位移超限。另外，从分析中可得，90°大风工况为最危险工况，而45°和90°风向角下应力响应均较大，因此绘制2种风向角下主材应力随高度变化的趋势如图15所示。

图  15  不同风向角下主材应力随高度变化

Figure 15.  The stress of main bars with height at different wind angles

在90°风向角下，输电塔的应力分布随高度变化呈现出一定的规律性：塔身根部（0 ～30 m）：应力最高，0 m高度处最大应力为115.35 MPa，10 m高度处为115.00 MPa，20 m高度处为107.99 MPa。而在横担对应处出现了一定的主材应力增大现象，此现象是由于横担上的风荷载导致横担根部的弯矩较大，因此主材的应力得到了一定的增大。在45°风向角下，输电塔的应力分布也表现出类似的规律性，但整体应力水平低于90°风向角。

分析不同风向角下的应力分布，可知塔身根部是最薄弱环节，不论是90°还是45°风向角，塔身根部（0～20 m）都是应力最高的部位，特别是在90°风向角下，最大应力达115.35 MPa。由于塔身根部支撑整个结构，受力集中且复杂，易发生破坏，应当在设计中关注强度指标。此外，对于与风向垂直的横担部位，风荷载将引起法兰连接处的较大弯矩，易造成主材应力增大，且由于风荷载为反复荷载，设计中需关注此处法兰连接的疲劳问题。

本文通过建立典型换向分支杆有限元模型并进行不同风向角下的风振响应分析，得到以下结论：

1）基于梁单元提出的换向分支杆简化有限元模型与壳单元模型具有相同的振动特征和近似的振动频率，证明了简化梁单元模型反映换向分支杆动力性能的有效性。

2）换向分支杆在风荷载作用下，主要的振动模式集中在一阶和二阶弯曲振型。换向分支杆结构的平均位移与导线的荷载直接相关，90°风向角为结构基于塔顶位移考虑的最不利工况。

3）90°风向角下，换向分支杆最大应力发生在塔身根部，表明横风对塔身的应力影响最为显著。此工况下最大塔顶位移达到最大且超过限值，因此换向分支杆的设计控制参数为塔顶位移。

4）在设计风速29 m/s不同风向角下，换向分支杆的稳定性满足要求，但是塔顶位移超过限值，已建设的应进行加固，计划建设的可考虑减小档距或增大截面以避免位移超限。