-
近年来，我国核电技术实现重大突破，自主创新和国产化水平显著提升，为全球核电安全与发展贡献了中国智慧[1-3]。堆芯安全是研发先进反应堆物理系统的首要出发点，燃料包壳则是堆芯安全的重要一环。核燃料包壳长时间工作在高温高压及强中子辐照环境中，保持包壳的结构完整性对于反应堆的安全运行非常重要[4]。FeCrAl合金以其优异的高温力学性能与抗辐照损伤能力成为耐事故核燃料包壳的候选替代材料[5-7]。核燃料包壳作为反应堆的核心结构材料，在长期服役过程中会发生高温蠕变、辐照蠕变现象，导致材料机械性能降低，严重影响核能安全。因此，耐事故燃料包壳用FeCrAl合金的蠕变性能对评价该材料性能至关重要。近年来，国内外学者对FeCrAl合金的热蠕变性能进行了一些试验和模拟研究。在试验研究方面，研究学者主要针对中高温和低应力条件下FeCrAl合金的热蠕变性能和变形机理进行了深入探讨。E. Arzt等[8]对FeCrAl合金的热蠕变性能进行了系统深入的研究，讨论了蠕变速率随应力的变化规律。J. Bessona等[9]研究发现，温度在1 073～1 173 K之间，应力低于25 MPa，FeCrAl合金的热蠕变速率更适合用Sellars-Tegart定律表示，而不是Norton定律。Kamikawa等[10]研究了在1 273 K时不同应力条件下FeCrAl合金的蠕变速率，进一步提出蠕变应力对应力因子的影响规律。应力区间20～160 MPa，高应力条件下应力因子n大致为20，中应力条件下减小到2左右。Yano等[11]研究发现在
1273 K以上的超高温下，添加Zr的FeCrAl合金薄壁管的抗拉强度和延伸率均高于未添加Zr的薄壁管。Gussev等[12]开展的原位爆管试验表明，在失水事故工况下几种核级FeCrAl合金应力因子n的变化区间为2.9～4.5。随着计算机模拟技术的发展，国内外学者利用分子动力学（Molecular Dynamics，MD）模拟研究了纳米晶体Cu[13]，Ni[14]，MgY合金[15]，NiZr合金[16]和FeNiCr合金[17]的高温蠕变行为，并得出蠕变本构参数随温度与应力的变化规律。Meraj等[18]模拟了具有双峰晶粒结构的纳米晶Ni的蠕变行为，并对不同蠕变阶段的微观结构演变进行了分析。结果表明，在细晶粒尺寸和分布相同的情况下，增大粗晶尺寸有利于提高双峰纳米晶Ni的高温抗蠕变性能。Pal[16]等人研究发现相比于纳米晶Ni和Zr随机分布的NiZr合金，晶界局部弥散Zr的纳米晶NiZr合金表现出更优异的抗蠕变性能，且抗蠕变性能随Zr原子体积分数的增加而逐渐增强。Zhao等人[19]研究了温度、应力和晶粒尺寸对纳米晶TiAl合金高温蠕变性能及机制的影响。研究发现，温度与应力越高或者晶粒尺寸越小，稳态阶段蠕变速率越大，蠕变过程进入第三阶段越迅速。此外，MD方法已成功地应用于纳米晶体Cu，Pd[20]和Si[21]的晶界扩散蠕变以及多种纳米级金属的塑性变形研究[22-23]。本文作者在前期开展了不同蠕变条件下FeCrAl合金热蠕变性能的模拟研究[24]，揭示了该合金高温蠕变速率及变形机理随温度、应力和晶粒尺寸等参数的演化规律。
中子辐照经济代价高昂、时间周期长且强活化，使得核能结构材料的辐照性能试验研究面临众多挑战。目前对核能材料辐照损伤行为的研究主要集中在微观尺度上。研究表明[25]，核能材料的中子辐照损伤主要起源于晶格原子的移位级联。载能中子将其绝大部分能量传递给晶格原子以激发碰撞级联，产生大量自间隙子和空位，这些点缺陷复合、聚集及与晶界等缺陷陷阱相互作用，最终演化造成材料微观结构变化与宏观力学性能退化。近年来，众多学者运用MD方法对材料辐照级联碰撞行为开展了系列研究，取得了一定进展。Zhang等人[26]和Sahi等人[27]分别模拟计算了α-Fe纳米线和α-Fe单晶的级联碰撞过程，分析了不同温度和中子辐照条件下点缺陷的空间分布及随时间的演化规律。Carlos等[28]研究了辐照级联过程对α-Fe晶界结构的影响。Igor等人[29]和Wong等人[30]研究指出，相比于纯α-Fe体系，由于Cr的加入FeCr合金表现出更高的抗辐照性能。随后，Malerba和Terentyevd等人[31-32]研究了FeCr合金体系的辐照损伤行为，结果表明，间隙原子团簇中存在的Cr会对由间隙原子组成的位错环的运动造成阻碍。FeCrAl合金是近年来提出的一种新型核燃料包壳材料，与FeCr合金体系相比，Al的加入使其具有更高的力学性能[33]。Ye等人[34]利用LAMMPS软件对FeCrAl合金体系的辐照级联过程进行了模拟分析，研究发现，与α-Fe相比，FeCrAl合金中Cr和Al的存在会导致稳定阶段残存的点缺陷数量增多，但降低了缺陷演化过程中形成的点缺陷团簇数。目前，针对高温-辐照条件下FeCrAl合金蠕变性能的研究仍然相对匮乏。基于此，本文对FeCrAl合金的热蠕变和辐照蠕变微观变形行为进行了模拟研究，探讨了温度、应力和辐照剂量率等参数对稳态蠕变速率的影响，进一步对蠕变本构方程的关键参数进行了深入的分析。
-
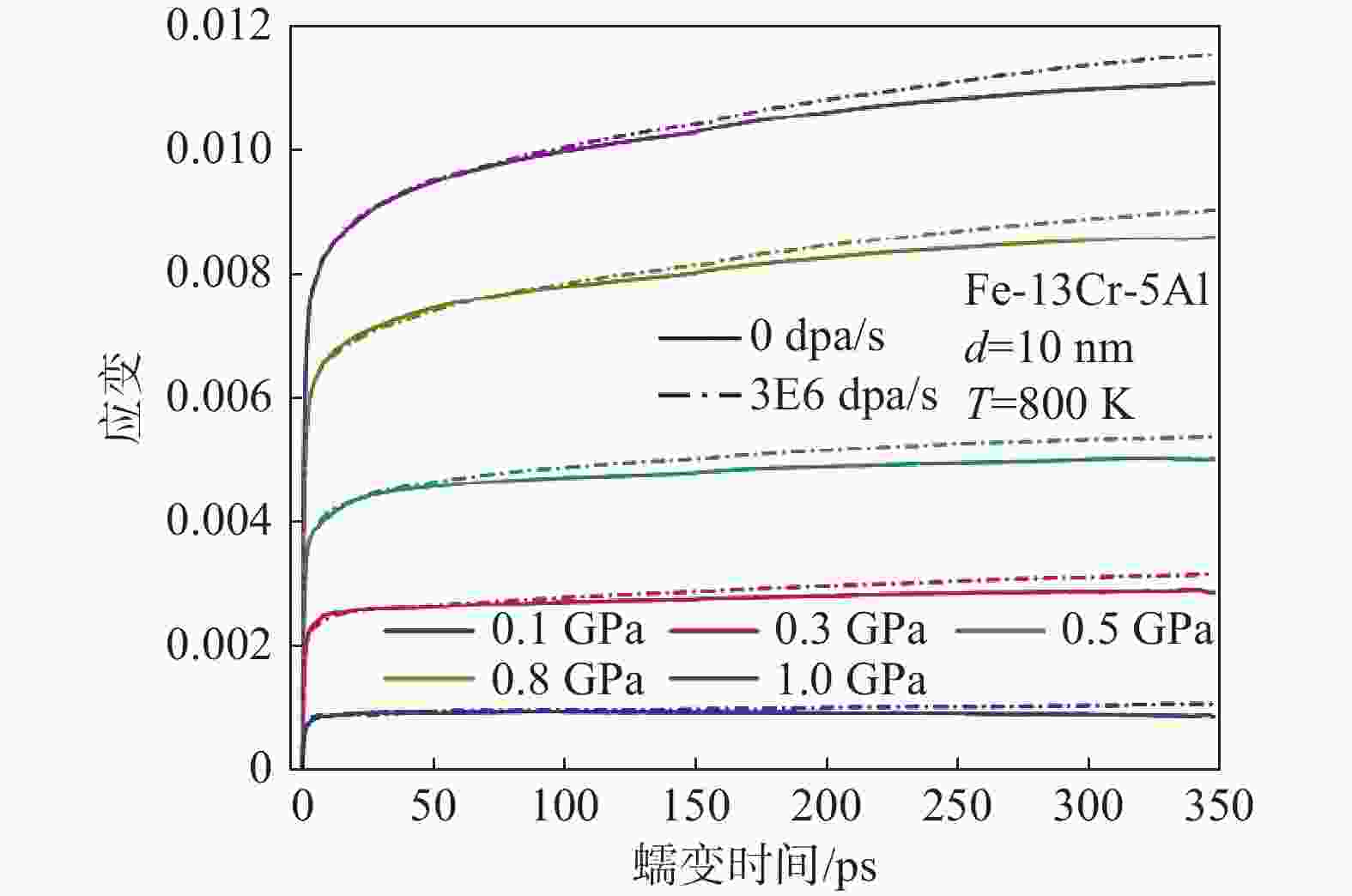
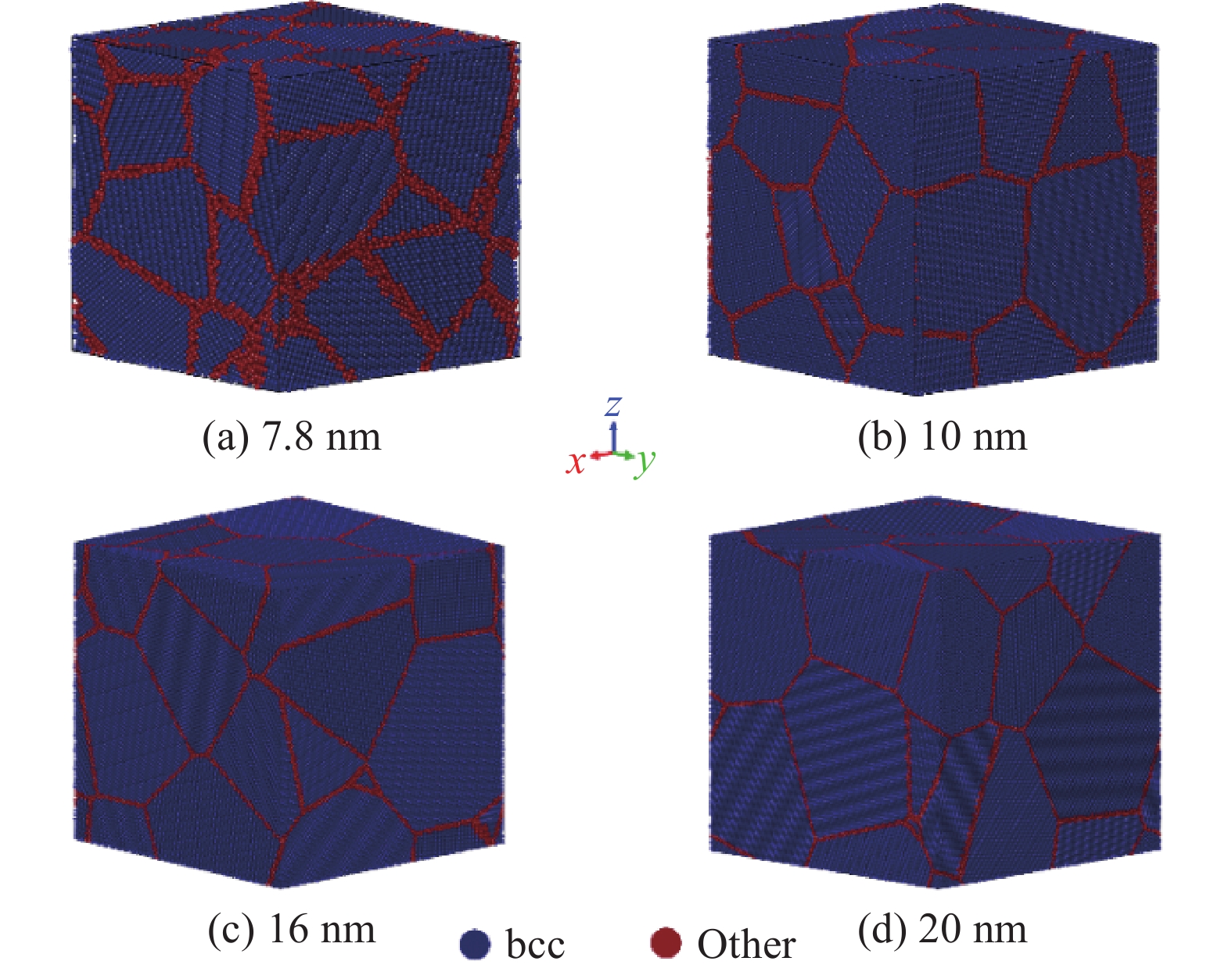
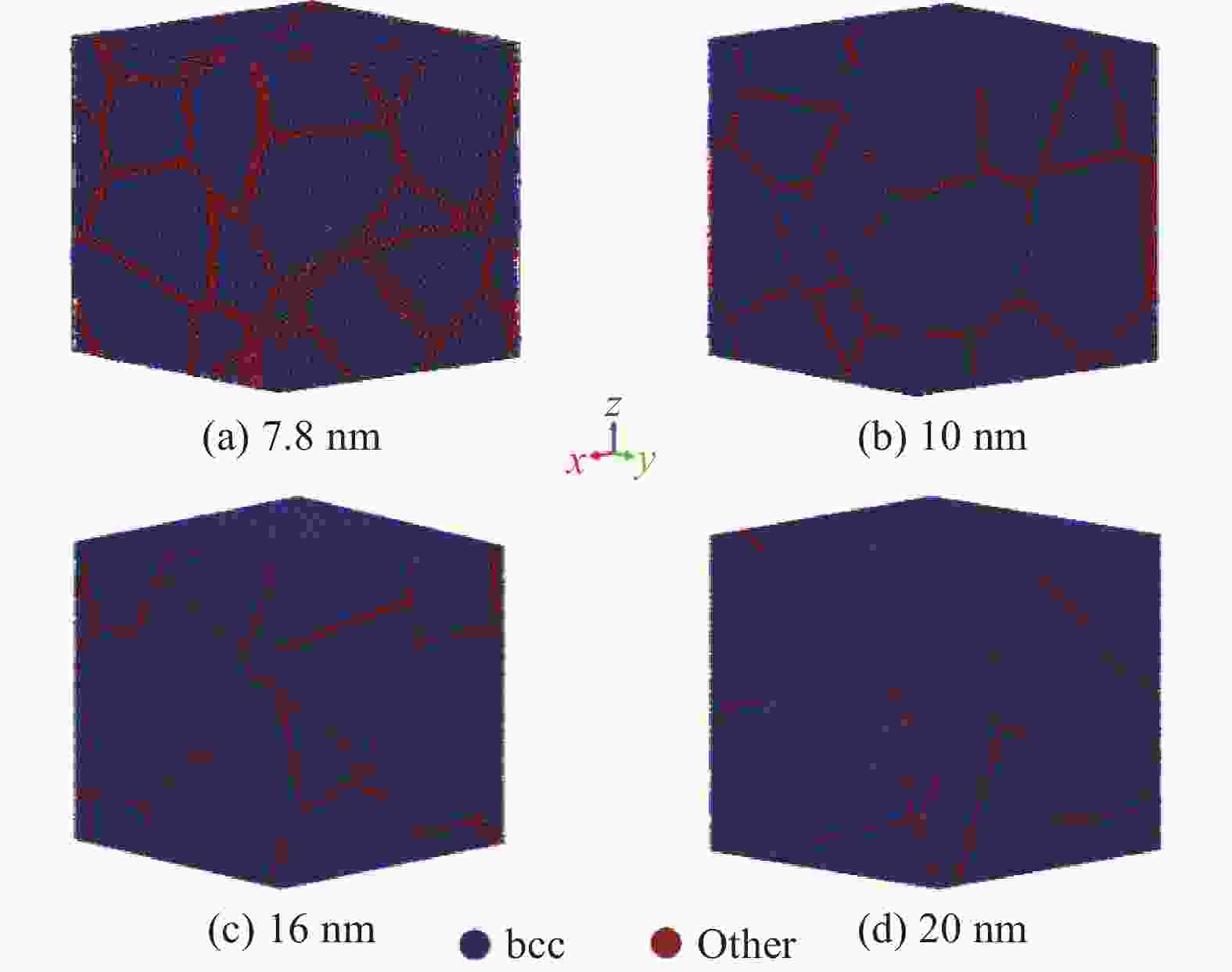
本文采用Atomsk[35]晶体建模软件，基于泰森多边形镶嵌法建立了晶粒尺寸区间为7.8～20 nm的FeCrAl合金纳米晶体模型，如图1所示。为了更好地展示计算模型的晶界和晶内区域，体心立方（Body-Centered Cubic，BCC）结构的原子以蓝色表示，其他结构（other）原子则以红色表示。所构建的模拟体系为正方体盒子，晶粒取向随机分布。表1列出了不同晶粒尺寸的FeCrAl合金纳米晶体计算模型参数。Yamamoto等人[5]基于对轻水堆燃料包壳用FeCrAl基合金材料的综合性能评估，确定出质量分数为13%的Cr和5%的Al为最佳成分配比。本文中所有样品的合金组分均设定为Fe-13Cr-5Al（wt%）。由于Cr和Al溶质原子均具有较低的空位形成能，FeCrAl合金通常以Fe基体心立方（bcc）置换固溶体的形式存在[36-37]。基于此，本文利用Python语言编程，通过在bcc结构的α-Fe基体中随机掺杂一定质量分数的Cr和Al，建立了Fe13Cr5Al合金样品的计算模型。
图 1 FeCrAl合金晶体模型
Figure 1. The models of FeCrAl samples
表 1 FeCrAl合金晶体模型参数
Table 1. Model parameters of FeCrAl samples.
晶粒尺寸d /nm 7.8 10 16 20 晶粒数目/个 12 12 8 8 原子数目/105 4.8 10.1 27.8 54.3 模拟盒子尺寸/nm 17.9 22.9 32.0 40.0 -
本文采用MD模拟软件LAMMPS[38]，基于Liao等人[39]开发的FeCrAl合金原子间相互作用EAM/FS势函数，对上述构建的FeCrAl合金纳米晶进行热蠕变与辐照蠕变微观模拟计算。在蠕变模拟计算前，采用共轭梯度法对晶体模型进行能量最小化计算，得到稳定初始构型。随后，相继采用NVT系综和NPT系综对模拟体系进行弛豫，弛豫时间为600～
3500 ps，时间步长0.001 ps。弛豫结束后，在NPT系综下对晶体模型进行蠕变变形模拟，以负压代替拉应力的方式在y轴施加0.1～2.0 GPa的蠕变应力，蠕变温度区间600～1 200 K。表2详细地列出了本文中使用的蠕变模拟参数。表 2 蠕变模拟参数
Table 2. Creep simulation parameters
晶粒尺寸d /nm 7.8 10 16 20 NVT/NPT弛豫时间/ps 600 1 000 2 500 3 500 蠕变温度T /K 600, 800, 1 000, 1 200 蠕变应力σ /GPa 0.1, 0.3, 0.5, 0.8, 1.0, 1.2, 1.5, 1.8, 2.0 辐照剂量率ϕ /dpa/s 0, 1E6, 2E6, 3E6, 4E6, 5E6, 6E6 辐照对蠕变过程的影响，主要表现为晶格原子的级联碰撞导致晶体内部产生高浓度的点缺陷及缺陷团簇，这些缺陷在高温蠕变过程扩散、复合和演化，对材料蠕变行为产生重要影响[34]。在辐照、热、外应力等作用下，点缺陷随时间演化造成材料力学性能退化。本文为了实现辐照蠕变过程模拟，在蠕变计算期间每间隔30 ps，依据辐照剂量率参数，在模型中随机引入相同数量的空位和自间隙原子。其中，剂量率区间0～6E6 dpa/s，蠕变模拟时间350 ps。模拟体系在3个方向均采用周期性边界条件。
-
鉴于稳态蠕变阶段持续时间较长，在总蠕变寿命中占比相对较高，通常采用稳态阶段的蠕变变形规律描述材料的蠕变特性。高温-辐照条件下FeCrAl合金的总蠕变速率为热蠕变速率与辐照蠕变速率的总和：
$$ \dot \varepsilon = {\dot \varepsilon _{{\text{th}}}} + {\dot \varepsilon _{{\text{ir}}}} $$ (1) 式中：
${\dot \varepsilon _{{\text{th}}}}$ ——热蠕变速率（s−1）；
${\dot \varepsilon _{{\text{ir}}}}$ ——辐照蠕变速率（s−1）。
Mukherjee和Bird等人[40]提出了热蠕变稳态阶段的蠕变本构方程，定义了热蠕变速率与温度、应力、晶粒尺寸以及材料本身性质之间的关系式[41]：
$$ {\dot \varepsilon _{{\text{th}}}} = \frac{{{A_{{\text{th}}}}{D_0}G{\text{b}}}}{{{{\text{k}}_{\text{B}}}T}}{\left( {\frac{{\text{b}}}{d}} \right)^p}{\left( {\frac{\sigma }{G}} \right)^{{n_{{\text{th}}}}}}exp\left( { - \frac{{{Q_{\text{c}}}}}{{{{\text{k}}_{\text{B}}}T}}} \right) $$ (2) 式中:
Ath ——热蠕变常数；
D0 ——扩散系数（m2/s）；
G ——剪切模量（MPa）；
b ——柏氏矢量（m）；
kB ——玻尔兹曼常数8.62×10−5（eV/K）；
T ——温度（K）；
Σ ——应力（MPa）；
d ——晶粒直径（m）；
Qc ——热蠕变激活能（eV）；
P ——热蠕变晶粒因子；
nth ——热蠕变应力因子。
辐照蠕变稳态阶段的蠕变速率与辐照剂量率ϕ和应力σ之间的关系遵循下式：
$$ {\dot \varepsilon _{{\text{ir}}}} = {A_{{\text{ir}}}}{\phi ^m}{\sigma ^{{n_{{\text{ir}}}}}} $$ (3) 式中：
ϕ ——辐照剂量率（dpa/s）；
Air ——辐照蠕变常数（MPa−1·dpa−1）；
m ——辐照剂量率因子；
nir ——辐照蠕变应力因子。
此外，nth和nir分别根据式（4）和式（5）计算得出：
$$ {n_{{\text{th}}}} = \frac{{\partial \log {{\dot \varepsilon }_{{\text{th}}}}}}{{\partial \log \sigma }} $$ (4) $$ {n_{{\text{ir}}}} = \frac{{\partial \log {{\dot \varepsilon }_{{\text{ir}}}}}}{{\partial \log \sigma }} $$ (5) -
通过比对不同蠕变条件下FeCrAl合金的蠕变变形曲线，探讨了温度、应力、辐照剂量率和晶粒尺寸等参数对蠕变速率的影响规律。不同温度条件下，辐照剂量率对蠕变曲线的影响规律如图2所示。图中可以看出，0～50 ps，蠕变速率随时间不断减少，即减速蠕变阶段或称蠕变第一阶段，之后蠕变速率保持不变，蠕变进入稳态蠕变阶段或称蠕变第二阶段。随着温度和辐照剂量率升高，FeCrAl合金的稳态蠕变速率不断增加。此外，随着温度的上升，蠕变速率随剂量率的增长速度逐渐加快。这可以解释如下：温度上升加快了晶格原子、空位及间隙原子扩散过程，使得晶界扩散和晶格扩散速率增加。另一方面，高温环境下提供了克服位错运动障碍的能量，最终导致蠕变变形量和变形速率增加。
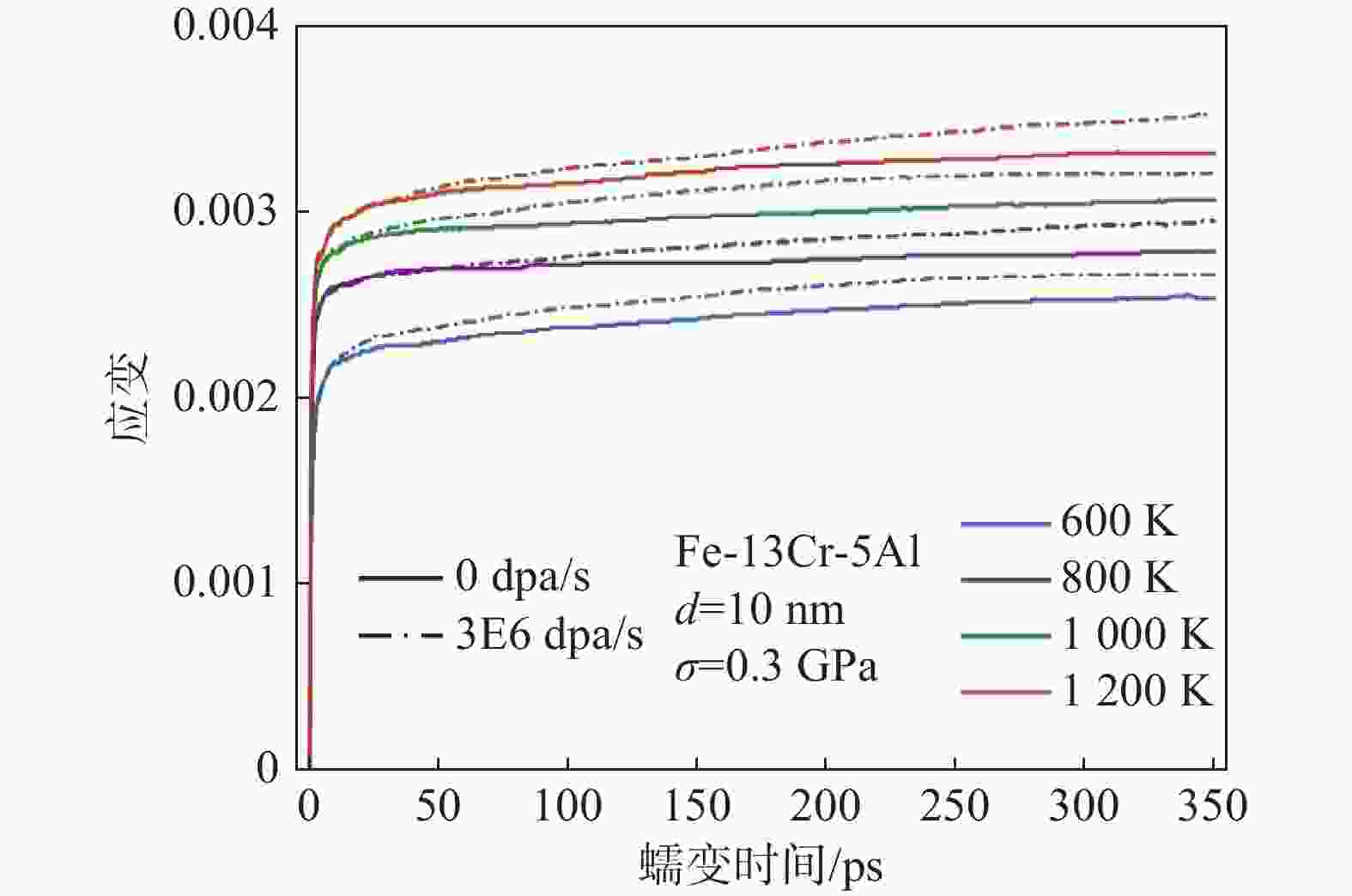
图 2 不同温度条件下辐照剂量率对蠕变曲线的影响
Figure 2. Creep curves under different temperatures and irradiation dose rates
图3是不同蠕变应力条件下，辐照剂量率对蠕变曲线的影响规律。图中可知，蠕变速率随着应力与剂量率升高而显著增加。随着蠕变应力的提高，蠕变速率随剂量率的增长速度逐渐加快。分析原因如下：在恒定的应力作用下，沿特定位错方向（相当于应力施加方向）辐照点缺陷产生不对等吸收，造成晶粒沿某个方向的生长即晶格膨胀，且晶界上会产生应力，导致材料强度下降和晶界断裂。随着蠕变应力的升高，辐照点缺陷非均匀吸收所引起的晶粒各向异性生长与晶界应力不断增加，蠕变变形量随之增加。
图 3 不同应力条件下辐照剂量率对蠕变曲线的影响
Figure 3. Creep curves under different stresses and irradiation dose rates
图4给出的不同蠕变时刻位错缺陷空间分布结果显示，晶体模型的刃位错密度明显高于螺位错，且随着蠕变过程的进行，刃位错数量不断减少。在蠕变外应力作用下，较大塑性变形下材料内部的空位浓度增加，刃位错攀移过程加快，柏氏矢量方向相反的刃型位错相遇会抵消，导致刃位错密度降低。图4还显示，随着蠕变过程的进行，位错总体密度也呈现不断下降的趋势。这是因为，在较高的外应力作用下，位错能够克服周围晶格阻力，位错会发生滑移和攀移运动，且位错运动速度随应力的增大而增大。此外，晶体模型的位错主要位于晶界区域，运动的位错更容易被晶界吸收而发生湮灭，使其密度不断降低。值得一提，晶界区域作为辐照产生点缺陷重要的源和阱，在高温和外应力作用下既可以释放大量的点缺陷，还有效吸收、捕获和湮灭辐照产生的点缺陷，以降低其能量。这说明外应力条件下，位错运动加快且位错密度有所降低。应力加载方向的位错运动速度与位错密度差异均会影响晶界和位错对辐照引入点缺陷的吸收效率，进而导致蠕变变形量发生改变。
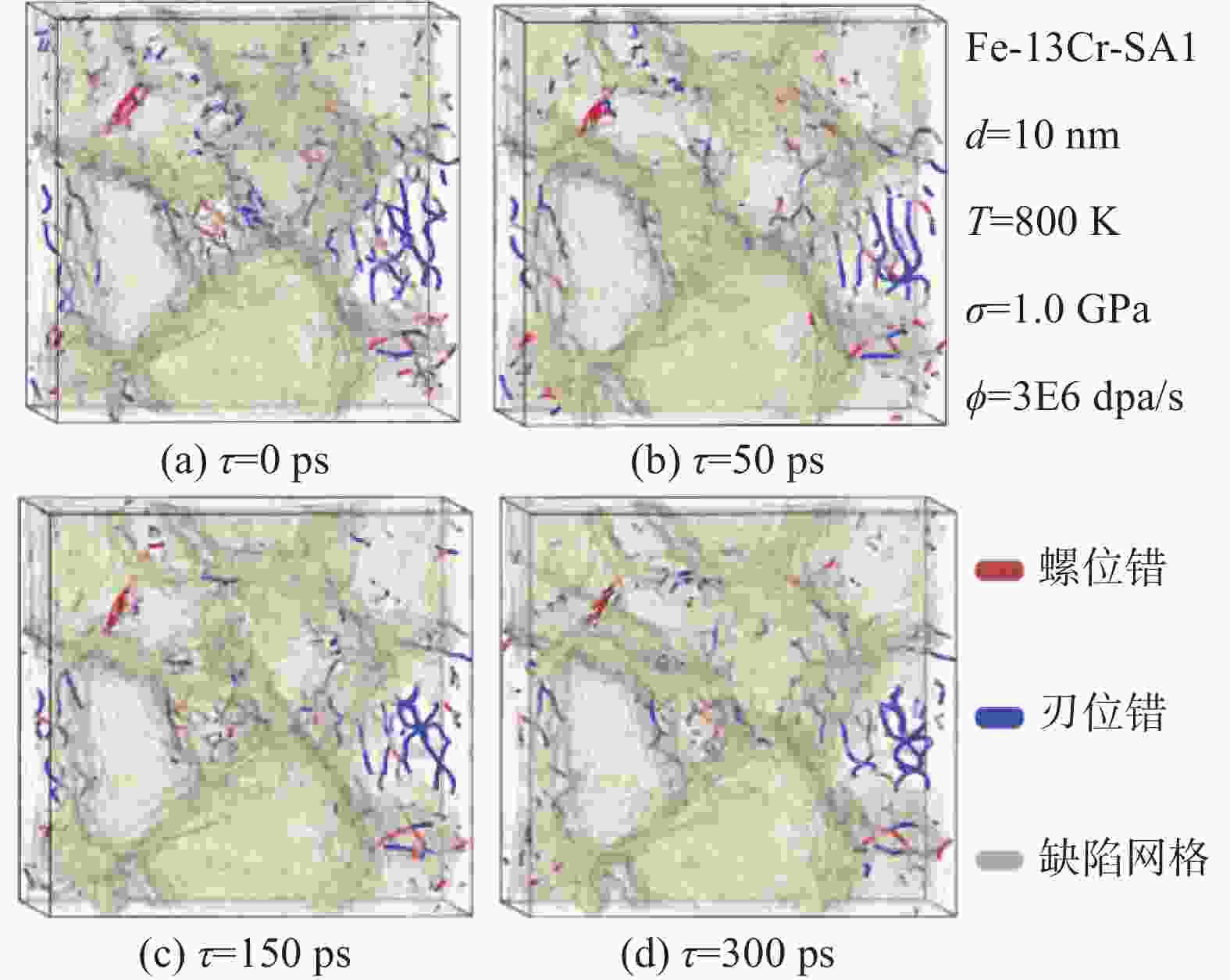
图 4 温度800 K应力1.0 GPa蠕变经历不同时长后晶体位错缺陷空间分布
Figure 4. Distribution of dislocations at different creep time (a) 0 ps, (b) 50 ps, (c) 150 ps, and (d) 300 ps at 800 K and 1.0 GPa
图5展示了不同晶粒尺寸条件下，辐照剂量率对蠕变曲线的影响规律。从图中可知，随着晶粒尺寸的增加，FeCrAl合金的稳态蠕变速率明显降低。对于纳米晶体材料而言，晶界作为重要的组元占有很大的体积分数，这使得空位、空位团和自间隙原子等点缺陷明显增多。随着晶粒尺寸的增加，晶界体积分数大幅度减少，晶体缺陷密度随之降低，使得材料的力学性能得到提高。这也能够从某种程度上解释FeCrAl合金纳米晶的蠕变速率随晶粒尺寸增加逐渐降低的原因。图5中还可以看出，随着晶粒尺寸的增加，蠕变速率随剂量率的增长速度明显加快。分析其原因如下：材料受中子辐照后产生了大量的自间隙子与空位，这些点缺陷在扩散、迁移过程中，通过与位错、晶界、空洞等相互作用发生复合、聚集和湮灭[42]。Zinkle等人[43]研究指出，晶界作为缺陷势阱能够显著地捕获、消除和吸收点缺陷，又称缺陷耗尽区。这表明辐照点缺陷从其产生处开始扩散，终止于缺陷势阱。随着晶粒尺寸的增加，晶界体积分数大幅度减少，使得点缺陷迁移过程中被晶界捕获、吸收的几率明显降低，辐照剂量率对蠕变速率的影响随之增加。
图 5 不同晶粒尺寸条件下辐照剂量率对蠕变曲线的影响
Figure 5. Creep curves under different grain sizes and irradiation dose rates
-
本文根据FeCrAl合金的蠕变速率随温度、应力和辐照剂量率等参数的变化规律，总结得出不同高温-中子辐照条件下的热蠕变应力因子nth，辐照蠕变应力因子nir、剂量率因子m和辐照蠕变常数Air。图6是晶粒尺寸为10 nm，不同温度条件下FeCrAl合金的稳态蠕变速率与应力的双对数关系曲线。从图中可以看出，随着蠕变应力升高，热蠕变速率随应力增长速度逐渐加快。应力区间在0.1～2.0 GPa，热蠕变应力因子nth随应力增加由0.9增至2.0左右，其中应力转折点为0.8 GPa。此外，在600～
1200 K的温度区间内，相比于应力，温度对热蠕变应力因子的影响相对较小。在不同的温度与应力条件下，辐照蠕变应力因子的变化幅度较小，nir基本在1.0附近波动。这表明，FeCrAl合金的辐照蠕变速率随应力增加呈线性增长趋势。通过比较不同蠕变条件下的热蠕变速率与辐照蠕变速率，容易得出热蠕变速率明显高于辐照蠕变速率。另一方面，蠕变应力因子n随应力的变化规律与热蠕变应力因子nth基本一致。以上分析可知，高温-辐照条件下FeCrAl合金的蠕变性能主要取决于热蠕变行为，而受辐照蠕变行为的影响相对较小。值得指出，热蠕变速率高于辐照蠕变速率，这一现象与文献报道的模拟结果一致[41]。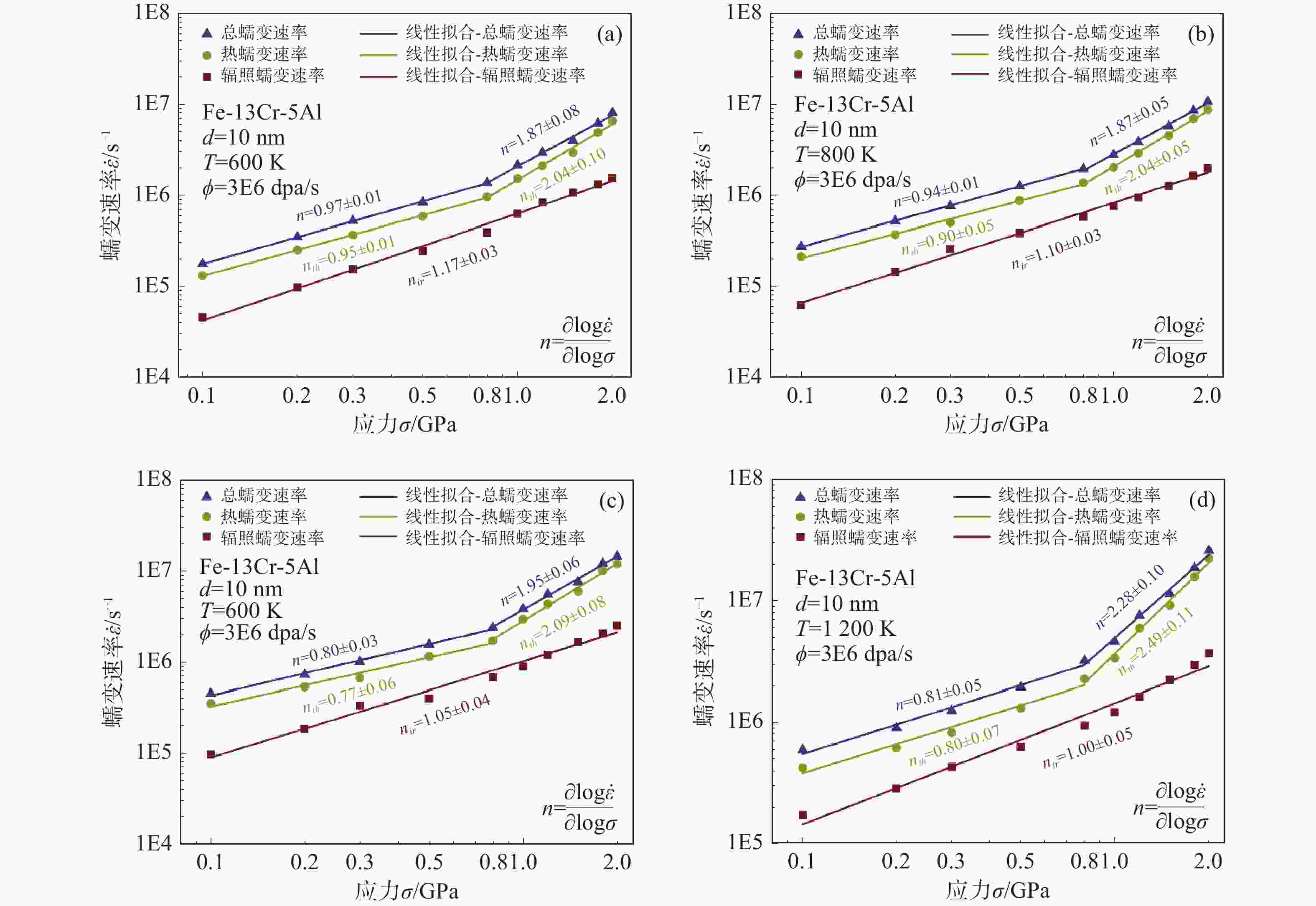
图 6 不同温度条件下蠕变速率与应力的双对数关系曲线
Figure 6. Double-logarithmic plots of the creep rate vs stress in the range of 0.1-2.0 GPa at different temperatures (a) 600 K (b) 800 K (c) 1 000 K (d) 1 200 K
由图6可见，纳米晶FeCrAl样品的热蠕变应力因子nth与通过MD方法获得的纳米晶Ni[14]、Cu[44]和Ti-Al合金[19]的模拟结果相近。国内外针对常见晶体材料的研究表明，应力因子的不同标志着蠕变机制的重要转变[45-49]。因此，通过nth的值可以推断蠕变变形的内在机制：当nth=2时，蠕变主要由晶界滑动引起，nth=1则意味着晶格扩散和晶界扩散成为蠕变变形的主要机制。结合图6可知，在低应力条件下，纳米晶FeCrAl的热蠕变机制主要由扩散蠕变控制。当应力增加到0.8至2.0 GPa时，蠕变机制转变为晶界滑动。这一发现与商用FeCrAl合金的最新实验结果相吻合，该研究指出，随着应力的降低，蠕变机制从传统的位错运动转变为伴随扩散蠕变的晶界滑动[10]。
目前，MD模拟结果与实际商用FeCrAl合金的实验数据相比，呈现出更高的蠕变速率和较低的应力因子。以下是对此现象的阐释：首先，MD模拟的时间步长极为精细，导致其时间尺度通常限于皮秒至纳秒级别。为了加速蠕变过程的早期阶段，模拟中施加了极高的应力，从而导致观测到的高蠕变速率。这一现象在相关文献的模拟研究中也得到了体现和证实[15, 17, 19, 50]。此外，MD模拟的模型尺寸相较于实验样品小了5个数量级，这表明计算模型实际上代表了实验样品的基本单元。因此，模拟中观察到的较高蠕变速率和较低应力因子，从理论模型与实际样品尺寸差异的角度来看，是合理且符合预期的。尽管MD模拟所获得的高蠕变速率不能直接应用于FeCrAl包壳材料在实际工况下的设计，但是纳米晶材料在高温及辐照环境中的蠕变本构参数，可以通过分析稳态蠕变速率与应力、辐照剂量率之间的变化关系来确立。近年来，众多研究者采用MD方法对纳米晶材料在高温条件下的蠕变行为和机理进行了深入研究。基于模拟结果，一些研究者已成功构建了适用于纳米晶金属和合金的蠕变本构模型[15, 17, 19, 50]。
本文进一步研究了不同温度条件下，FeCrAl合金的辐照蠕变速率随剂量率参数的变化规律，如图7所示。从图中可以看出，当蠕变温度和应力保持恒定，随着辐照剂量率的增加，FeCrAl合金的辐照蠕变速率呈线性增长趋势。不同蠕变温度条件下，辐照蠕变速率随剂量率增加呈线性增长这一变化特征，也表明了辐照蠕变本构方程的剂量率因子m大致为1。根据辐照蠕变速率与剂量率的线性拟合斜率值k，本文进一步推断得出辐照蠕变常数Air，见图7。从图中可知，随着蠕变温度的升高，辐照蠕变常数Air逐渐增加。当温度从600 K上升至
1200 K，Air由2.77×10−4增加至4.76×10−4。这表明，随着温度的上升，辐照蠕变速率随剂量率的增长速度明显加快，即辐照蠕变速率对中子辐照剂量的敏感性逐渐增强。基于以上，温度与应力升高加快了该合金的辐照蠕变过程。综合图6与图7可以得出，高温-中子辐照条件下FeCrAl合金的热蠕变速率明显高于辐照蠕变速率，蠕变性能主要取决于热蠕变行为，受辐照蠕变行为的影响相对较小。随着蠕变应力升高，热蠕变应力因子由0.9增至2.0左右，其中应力转折点为0.8 GPa。相比于应力，蠕变温度对热蠕变应力因子的影响相对较小。在不同的温度与应力条件下，辐照蠕变应力因子的变化幅度较小，nir基本在1.0附近波动。当蠕变温度和应力保持恒定，辐照蠕变速率随着剂量率增加呈线性增长规律，即剂量率因子m大致为1.0。随着温度的上升，辐照蠕变速率随剂量率的线性增长速度逐渐增大，辐照蠕变常数Air随之增加。这意味着热蠕变与辐照蠕变之间存在显著的相互作用，两者相互增强，大幅提升了材料蠕变损伤的严重程度。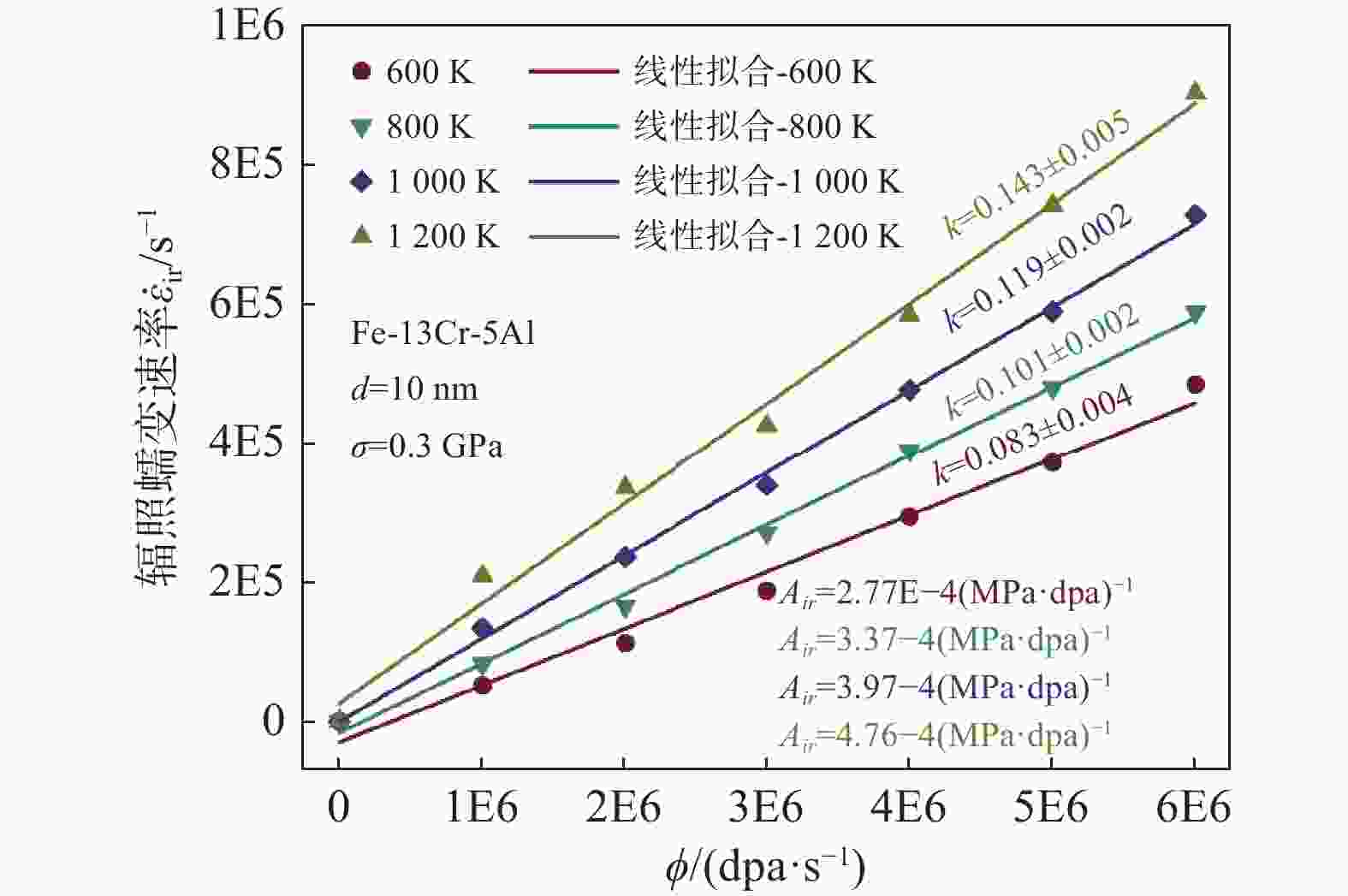
图 7 不同温度条件下辐照蠕变速率与剂量率的关系曲线
Figure 7. Plots of the irradiation creep rate vs dose rate at different temperatures
本文拟合得到的FeCrAl合金高温-辐照蠕变本构方程中的nir和m值与美国橡树岭国家实验室（Oak Ridge National Laboratory，ORNL）的堆内实验结果相一致[7, 41]。基于他们的堆内实验数据，FeCrAl包壳的辐照蠕变剂量率因子m和应力因子nir均等于1.0。值得一提，在纳米晶Cu样品的MD模拟中也得到了类似的结果[51]。研究发现，辐照剂量率在5×105～6×106 dpa/s范围内，辐照蠕变速率随剂量率增加呈线性增加趋势。在较宽的应力范围内，辐照蠕变速率与所施加的应力也呈线性关系。此外，本文拟合得到的辐照蠕变常数Air与文献中纳米晶Cu样品的模拟结果也非常吻合[51]。研究发现，平均晶粒尺寸为6 nm的纳米晶Cu样品，当温度为300 K，辐照剂量率为3×106 dpa/s，Air约为4.8×10−4 MPa−1dpa−1[51]。如图6所示，对于晶粒尺寸10 nm的纳米晶FeCrAl样品，温度600～
1200 K范围内，Air大致由2.77×10−4 MPa−1dpa−1增至4.76×10−4 MPa−1dpa−1。基于上述结果与讨论，本研究小组将进一步探讨FeCrAl合金的高温-辐照蠕变机制，以为FeCrA包壳的设计和服役期内辐照的影响分析提供支持。 -
本文利用MD方法模拟研究了高温-中子辐照条件下FeCrAl合金的蠕变性能，探讨了温度、应力和辐照剂量率等参数对蠕变速率的影响规律，进一步对蠕变本构方程的关键参数进行了深入的分析。主要得出以下结论：
1）高温-中子辐照条件下FeCrAl合金的热蠕变速率明显高于辐照蠕变速率，蠕变性能主要取决于热蠕变变形行为，受辐照蠕变行为的影响相对较小。随着蠕变温度、应力的升高，或晶粒尺寸的降低，蠕变速率明显增加，且蠕变速率随辐照剂量率的增长速度逐渐加快。
2）随着蠕变应力升高，热蠕变速率随应力增长速度逐渐加快。应力区间在0.1～2.0 GPa，热蠕变应力因子nth随应力增加由0.9增至2.0左右，应力转折点为0.8 GPa。相比于应力，蠕变温度对热蠕变应力因子的影响相对较小。
3）辐照蠕变速率随着剂量率的增加呈线性增长趋势，即剂量率因子m为1.0。在不同的温度与应力条件下，辐照蠕变应力因子的变化幅度较小，nir基本在1.1附近波动。随着温度的上升，辐照蠕变速率随剂量率的线性增长速度逐渐增大，辐照蠕变常数随之增加。
基于分子动力学模拟研究FeCrAl合金高温-辐照蠕变行为
DOI: 10.16516/j.ceec.2024-398
CSTR: 32391.14.j.ceec.2024-398
作者简介:
通讯作者:
Thermal and Irradiation Creep Behavior of FeCrAl Alloy Based on Molecular Dynamics Simulation
-
摘要:
目的 FeCrAl合金以其优良的高温力学性能、抗辐照损伤能力与较高的制备技术成熟度成为耐事故核燃料包壳的候选材料。由于中子辐照代价高、周期长、测试难，该合金的高温-辐照蠕变的相关研究较少。文章研究该合金的高温蠕变和辐照蠕变行为，讨论辐照剂量率、温度及应力等参数对蠕变速率及蠕变本构参数的影响。 方法 通过建立不同晶粒尺寸FeCrAl合金晶体计算模型，采用分子动力学模拟软件LAMMPS，开展了较宽温度、应力和辐照剂量率范围内该合金的蠕变行为模拟。 结果 相比于高温蠕变速率，辐照蠕变速率明显较低。随着蠕变应力升高，高温蠕变速率随应力增长速度逐渐加快，蠕变应力因子由0.9增至2.0左右，其中应力转折点为0.8 GPa。辐照蠕变速率随应力和辐照剂量率的增加呈线性增长趋势，即辐照蠕变应力因子与剂量率因子都接近1.0。随着温度的上升，辐照蠕变速率随剂量率的线性增长速度逐渐增大，辐照蠕变常数随之增加。 结论 高温-辐照条件下FeCrAl合金的蠕变性能主要取决于热蠕变行为，且温度与应力升高加快了该合金的辐照蠕变过程。 Abstract:Objective FeCrAl alloys have shown promise as candidate materials for accident tolerance fuel cladding because of their excellent high-temperature strength, irradiation resistance, and mature fabrication technology. There are fewer studies related to the thermal and irradiation creep of FeCrAl alloys due to the high cost, long cycle time and difficult testing of neutron irradiation. The thermal and irradiation creep behavior of FeCrAl alloys were examined. And, the effects of irradiation dose rate, temperature and stress on the creep rate and parameters of the creep constitutive equations were analyzed. Method The creep simulations were performed on several FeCrAl samples with different grain sizes over a wide range of temperature, stress, and irradiation dose rates, using LAMMPS molecular dynamics simulator. Result The results show that the irradiation creep rate is significantly lower, compared to the thermal creep rate. As stress rises, the thermal creep rate increases exponentially, and the stress exponent increases roughly from 0.9 to 2.0 at the turning point of 0.8 GPa. The irradiation creep rate increases linearly with stress and dose rate, that is, the exponents of both dose rate and stress for irradiation creep are very close to 1.0. Besides, higher temperatures accelerates the linear increase of irradiation creep rate with dose rate, and the irradiation creep pre-factor becomes larger. Conclusion The creep of FeCrAl alloys under conditions of high temperature and irradiation is mainly attributed to the thermal creep behavior. Higher temperatures and stresses accelerate the irradiation creep process. -
Key words:
- irradiation creep /
- high-temperature creep /
- fuel cladding /
- molecular dynamic
-
图 2 不同温度条件下辐照剂量率对蠕变曲线的影响
Fig. 2 Creep curves under different temperatures and irradiation dose rates
图 3 不同应力条件下辐照剂量率对蠕变曲线的影响
Fig. 3 Creep curves under different stresses and irradiation dose rates
图 4 温度800 K应力1.0 GPa蠕变经历不同时长后晶体位错缺陷空间分布
Fig. 4 Distribution of dislocations at different creep time (a) 0 ps, (b) 50 ps, (c) 150 ps, and (d) 300 ps at 800 K and 1.0 GPa
图 5 不同晶粒尺寸条件下辐照剂量率对蠕变曲线的影响
Fig. 5 Creep curves under different grain sizes and irradiation dose rates
图 6 不同温度条件下蠕变速率与应力的双对数关系曲线
Fig. 6 Double-logarithmic plots of the creep rate vs stress in the range of 0.1-2.0 GPa at different temperatures (a) 600 K (b) 800 K (c) 1 000 K (d) 1 200 K
图 7 不同温度条件下辐照蠕变速率与剂量率的关系曲线
Fig. 7 Plots of the irradiation creep rate vs dose rate at different temperatures
表 1 FeCrAl合金晶体模型参数
Tab. 1. Model parameters of FeCrAl samples.
晶粒尺寸d /nm 7.8 10 16 20 晶粒数目/个 12 12 8 8 原子数目/105 4.8 10.1 27.8 54.3 模拟盒子尺寸/nm 17.9 22.9 32.0 40.0 
下载: 导出CSV
表 2 蠕变模拟参数
Tab. 2. Creep simulation parameters
晶粒尺寸d /nm 7.8 10 16 20 NVT/NPT弛豫时间/ps 600 1 000 2 500 3 500 蠕变温度T /K 600, 800, 1 000, 1 200 蠕变应力σ /GPa 0.1, 0.3, 0.5, 0.8, 1.0, 1.2, 1.5, 1.8, 2.0 辐照剂量率ϕ /dpa/s 0, 1E6, 2E6, 3E6, 4E6, 5E6, 6E6
下载: 导出CSV
-
[1] 高鹏. 华龙一号安全重要压力变送器设备鉴定研究 [J]. 南方能源建设, 2022, 9(2): 107-112. DOI: 10.16516/j.gedi.issn2095-8676.2022.02.015. GAO P. Research on equipment qualification for pressure transmitter important to safety of HPR1000 [J]. Southern energy construction, 2022, 9(2): 107-112. DOI: 10.16516/j.gedi.issn2095-8676.2022.02.015. [2] 雷川, 程鹏, 张智军. 高温气冷堆示范工程反应堆保护系统调试工具研发与应用 [J]. 南方能源建设, 2023, 10(6): 153-159. DOI: 10.16516/j.gedi.issn2095-8676.2023.06.018. LEI C, CHENG P, ZHANG Z J. R&D and application of commissioning tools for reactor protection system of high-temperature gas-cooled reactor-pebble-bed module [J]. Southern energy construction, 2023, 10(6): 153-159. DOI: 10.16516/j.gedi.issn2095-8676.2023.06.018. [3] 张玉祯, 廖佰凤, 汪静, 等. 压水堆核电站工业供汽系统技术可行性研究 [J]. 南方能源建设, 2022, 9(2): 120-124. DOI: 10.16516/j.gedi.issn2095-8676.2022.02.017. ZHANG Y Z, LIAO B F, WANG J, et al. Feasibility research in the technology for industrial steam supply by PWR nuclear power plant [J]. Southern energy construction, 2022, 9(2): 120-124. DOI: 10.16516/j.gedi.issn2095-8676.2022.02.017. [4] 孙婧, 马秀歌, 陈巧艳. 事故后安全壳内环境条件计算分析 [J]. 南方能源建设, 2015, 2(4): 53-56. DOI: 10.16516/j.gedi.issn2095-8676.2015.04.008. SUN J, MA X G, CHEN Q Y. Computational analysis of environment condition inside containment after accident [J]. Southern energy construction, 2015, 2(4): 53-56. DOI: 10.16516/j.gedi.issn2095-8676.2015.04.008. [5] YAMAMOTO Y, PINT B A, TERRANI K A, et al. Development and property evaluation of nuclear grade wrought FeCrAl fuel cladding for light water reactors [J]. Journal of nuclear materials, 2015, 467: 703-716. DOI: 10.1016/j.jnucmat.2015.10.019. [6] DRYEPONDT S, UNOCIC K A, HOELZER D T, et al. Development of low-Cr ODS FeCrAl alloys for accident-tolerant fuel cladding [J]. Journal of nuclear materials, 2018, 501: 59-71. DOI: 10.1016/j.jnucmat.2017.12.035. [7] QIU B W, WANG J, DENG Y B, et al. A review on thermohydraulic and mechanical-physical properties of SiC, FeCrAl and Ti3SiC2 for ATF cladding [J]. Nuclear engineering and technology, 2020, 52(1): 1-13. DOI: 10.1016/j.net.2019.07.030. [8] ARTZ E. Creep of dispersion strengthened materials: a critical assessment [J]. Res mechanica, 1991, 31: 399-453. DOI: 10.22028/D291-23975. [9] BÉRARD P, BARTOUT J D, REYTIER M, et al. Viscoplastic behavior of a FeCrAl alloy for high temperature steam electrolysis (HTSE) sealing applications between 700°C and 900°C [J]. Materials science and engineering A, 2011, 528(12): 4092-4097. DOI: 10.1016/j.msea.2011.01.050. [10] KAMIKAWA R, UKAI S, KASAI S, et al. Cooperative grain boundary sliding in creep deformation of FeCrAl-ODS steels at high temperature and low strain rate [J]. Journal of nuclear materials, 2018, 511: 591-597. DOI: 10.1016/j.jnucmat.2018.04.050. [11] YANO Y, TANNO T, OKA H, et al. Ultra-high temperature tensile properties of ODS steel claddings under severe accident conditions [J]. Journal of nuclear materials, 2017, 487: 229-237. DOI: 10.1016/j.jnucmat.2017.02.021. [12] GUSSEV M N, BYUN T S, YAMAMOTO Y, et al. In-situ tube burst testing and high-temperature deformation behavior of candidate materials for accident tolerant fuel cladding [J]. Journal of nuclear materials, 2015, 466: 417-425. DOI: 10.1016/j.jnucmat.2015.08.030. [13] WANG Y J, ISHII A, OGATA S. Grain size dependence of creep in nanocrystalline copper by molecular dynamics [J]. Materials transactions, 2012, 53(1): 156-160. DOI: 10.2320/matertrans.MD201122. [14] NIE K, WU W P, ZHANG X L, et al. Molecular dynamics study on the grain size, temperature, and stress dependence of creep behavior in nanocrystalline nickel [J]. Journal of materials science, 2017, 52(4): 2180-2191. DOI: 10.1007/s10853-016-0506-3. [15] BHATIA M A, MATHAUDHU S N, SOLANKI K N. Atomic-scale investigation of creep behavior in nanocrystalline Mg and Mg-Y alloys [J]. Acta materialia, 2015, 99: 382-391. DOI: 10.1016/j.actamat.2015.07.068. [16] PAL S, MERAJ M, DENG C. Effect of Zr addition on creep properties of ultra-fine grained nanocrystalline Ni studied by molecular dynamics simulations [J]. Computational materials science, 2017, 126: 382-392. DOI: 10.1016/j.commatsci.2016.10.013. [17] PAL S, MERAJ M. Structural evaluation and deformation features of interface of joint between nano-crystalline Fe-Ni-Cr alloy and nano-crystalline Ni during creep process [J]. Materials & design, 2016, 108: 168-182. DOI: 10.1016/j.matdes.2016.06.086. [18] MERAJ M, PAL S. Nano-scale simulation based study of creep behavior of bimodal nanocrystalline face centered cubic metal [J]. Journal of molecular modeling, 2017, 23(11): 309. DOI: 10.1007/s00894-017-3481-y. [19] ZHAO F, ZHANG J, HE C W, et al. Molecular dynamics simulation on creep behavior of nanocrystalline TiAl alloy [J]. Nanomaterials, 2020, 10(9): 1693. DOI: 10.3390/nano10091693. [20] YAMAKOV V, WOLF D, PHILLPOT S R, et al. Grain-boundary diffusion creep in nanocrystalline palladium by molecular-dynamics simulation [J]. Acta materialia, 2002, 50(1): 61-73. DOI: 10.1016/S1359-6454(01)00329-9. [21] KEBLINSKI P, WOLF D, GLEITER H. Molecular-dynamics simulation of grain-boundary diffusion creep [J]. Interface science, 1998, 6(3): 205-212. DOI: 10.1023/A:1008664218857. [22] YAMAKOV V, WOLF D, PHILLPOT S R, et al. Deformation-mechanism map for nanocrystalline metals by molecular-dynamics simulation [J]. Nature materials, 2004, 3(1): 43-47. DOI: 10.1038/nmat1035. [23] ZHANG F, LIU Z, ZHOU J Q. Molecular dynamics simulation of micro-mechanical deformations in polycrystalline copper with bimodal structures [J]. Materials letters, 2016, 183: 261-264. DOI: 10.1016/j.matlet.2016.07.122. [24] YAO H, YE T Z, YU W S, et al. Atomic-scale investigation of creep behavior and deformation mechanism in nanocrystalline FeCrAl alloys [J]. Materials & design, 2021, 206: 109766. DOI: 10.1016/j.matdes.2021.109766. [25] 郁金南. 材料辐照效应 [M]. 北京: 化学工业出版社, 2007: 32-137. YU J N. Radiation effects of materials [M]. Beijing: Chemical Industry Press, 2007: 132-137. [26] ZHANG M, PENG W X, ZHANG H L, et al. The effect of PKA directions on the primary radiation damage in the alpha iron nanowires [J]. Materials chemistry and physics, 2019, 232: 16-22. DOI: 10.1016/j.matchemphys.2019.04.038. [27] SAHI Q U A, KIM Y S. Primary radiation damage characterization of α-iron under irradiation temperature for various PKA energies [J]. Materials research express, 2018, 5(4): 046518. DOI: 10.1088/2053-1591/aabb6f. [28] CAMPAÑÁ C, BOYLE K P, MILLER R E. Grain boundary motion assisted via radiation cascades in bcc Fe [J]. Physical review B, 2008, 78(13): 134114. DOI: 10.1103/PhysRevB.78.134114. [29] ABRIKOSOV I A, PONOMAREVA A V, BARANNIKOVA S A, et al. Multiscale approach to theoretical simulations of materials for nuclear energy applications: Fe-Cr and Zr-based alloys [J]. MRS online proceedings library, 2013, 1514(1): 3-14. DOI: 10.1557/opl.2013.43. [30] WONG K L, LEE H J, SHIM J H, et al. Multiscale modeling of point defect interactions in Fe–Cr alloys [J]. Journal of nuclear materials, 2009, 386-388: 227-230. DOI: 10.1016/j.jnucmat.2008.12.092. [31] MALERBA L, TERENTYEV D, OLSSON P, et al. Molecular dynamics simulation of displacement cascades in Fe-Cr alloys [J]. Journal of nuclear materials, 2004, 329-333: 1156-1160. DOI: 10.1016/j.jnucmat.2004.04.270. [32] TERENTYEV D, MALERBA L, BARASHEV A V. On the correlation between self-interstitial cluster diffusivity and irradiation-induced swelling in Fe-Cr alloys [J]. Philosophical magazine letters, 2005, 85(11): 587-594. DOI: 10.1080/09500830500383563. [33] EDMONDSON P D, BRIGGS S A, Y. YAMAMOTO N, et al. Irradiation-enhanced α′ precipitation in model FeCrAl alloys [J]. Scripta materialia, 2016, 116: 112-116. DOI: 10.1016/j.scriptamat.2016.02.002. [34] YE T Z, YAO H, WU Y W, et al. Primary radiation damage characteristics in displacement cascades of FeCrAl alloys [J]. Journal of nuclear materials, 2021, 549: 152909. DOI: 10.1016/j.jnucmat.2021.152909. [35] HIREL P. Atomsk: A tool for manipulating and converting atomic data files [J]. Computer physics communications, 2015, 197: 212-219. DOI: 10.1016/j.cpc.2015.07.012. [36] AGHAMIRI S M S, SOWA T, UKAI S, et al. Microstructure and texture evolution and ring-tensile properties of recrystallized FeCrAl ODS cladding tubes [J]. Materials science and engineering: A, 2020, 771: 138636. DOI: 10.1016/j.msea.2019.138636. [37] AMARA H, FU C C, SOISSON R, et al. Aluminum and vacancies in α-iron: Dissolution, diffusion, and clustering [J]. Physical review B, 2010, 81(17): 174101. DOI: 10.1103/PhysRevB.81.174101. [38] PLIMPTON, STEVE, THOMPSON, et al. Molecular dynamics simulations from SNL's large-scale atomic/molecular massively parallel simulator (LAMMPS) [J]. 2011. (查阅网上资料, 未找到本条文献信息, 请确认) [39] LIAO X C, GONG H F, CHEN Y C, et al. Interatomic potentials and defect properties of Fe–Cr–Al alloys [J]. Journal of nuclear materials, 2020, 541: 152421. DOI: 10.1016/j.jnucmat.2020.152421. [40] MUKHERJEE A K, BIRD J E, DORN J E. Experimental correlations for high-temperature creep [J]. ASM transactions quarterly, 1969, 62(1): 155. [41] SWEET R T, GEORGE N M, MALDONADO G I, et al. Fuel performance simulation of iron-chrome-aluminum (FeCrAl) cladding during steady-state LWR operation [J]. Nuclear engineering and design, 2018, 328: 10-26. DOI: 10.1016/j.nucengdes.2017.11.043. [42] KWON J, KIM W, HONG J H. Comparison of the primary damage states in iron and nickel by molecular dynamics simulations [J]. Radiation Effects and Defects in Solids, 2006, 161(4): 207-218. DOI: 10.1080/10420150600704013. [43] ZINKLE S J. Microstructure of ion irradiated ceramic insulators [J]. Nuclear instruments and methods in physics research section B: beam interactions with materials and atoms, 1994, 91(1/4): 234-246. DOI: 10.1016/0168-583X(94)96224-3. [44] WANG Y J, ISHII A, OGATA S. Transition of creep mechanism in nanocrystalline metals [J]. Physical review B, 2011, 84(22): 224102. DOI: 10.1103/PhysRevB.84.224102. [45] NABBARRO F R N. Deformation of crystals by motion of single ions [R]. London: Physical Society, 1948: 1-19. [46] HERRING C. Diffusional viscosity of a polycrystalline solid [J]. Journal of applied physics, 1950, 21(5): 437-445. DOI: 10.1063/1.1699681. [47] COBLE R L. A model for boundary diffusion controlled creep in polycrystalline materials [J]. Journal of applied physics, 1963, 34(6): 1679-1682. DOI: 10.1063/1.1702656. [48] GIFKINS R C. Diffusional creep mechanisms [J]. Journal of the American ceramic society, 1968, 51(2): 69-72. DOI: 10.1111/j.1151-2916.1968.tb11838.x. [49] LÜTHY H, WHITE R A, SHERBY O D. Grain boundary sliding and deformation mechanism maps [J]. Materials science and engineering, 1979, 39(2): 211-216. DOI: 10.1016/0025-5416(79)90060-0. [50] PAL S, REDDY K V, SPEAROT D E. Zr segregation in Ni-Zr alloy: implication on deformation mechanism during shear loading and bending creep [J]. Journal of materials science, 2020, 55(14): 6172-6186. DOI: 10.1007/s10853-020-04411-1. [51] ASHKENAZY Y, AVERBACK R S. Irradiation induced grain boundary flow-a new creep mechanism at the nanoscale [J]. Nano letters, 2012, 12(8): 4084-4089. DOI: 10.1021/nl301554k. -
图(7) / 表 (2)
计量
- 文章访问数: 26
- HTML全文浏览量: 13
- PDF下载量: 0
- 被引次数: 0
