-
大力发展新能源,实现能源生产向新能源转型,是我国经济与能源可持续发展的必然选择,提高新能源接入比例也将成为我国电力系统发展的主要任务和核心目标之一[1-2]。但是,高比例新能源发电和大量新型负荷采用电力电子装置接入系统,系统与源、荷之间的接口将呈现高度电力电子化特征,使得未来新型电力系统在扰动后的动态响应和频率调节过程呈现出与传统系统迥然不同的特征[3-6]。
与常规同步发电机组不同,通过电力电子接口接入系统的风电、光伏等新能源发电装置基本不具备惯性支撑能力:出于风机叶片安全和经济性的考虑,基于常规控制的风电机组较少提供扰动瞬间降低电网频率波动的惯量响应;而光伏发电的可控性及储能性能微弱,与系统频率完全解耦,不考虑特定控制措施则无法进行惯量响应[5];而直流输电虽然具备功率调整能力,但是通常不考虑其在扰动后瞬间的惯量响应。
在负荷侧,电力电子接口的非线性负荷比例也在持续提升,如充电桩、变频电机等。此类负荷的频率响应与传统异步机有极大的差异,受控电力电子接口的负荷在各类约束范围内几乎不响应频率变化,无法为系统提供惯量支撑[7-10]。
源、荷侧与电网接口的电力电子化趋势使电力系统呈现出了越来越明显的低惯量特征[1-2]。近年来,国内外多个新能源渗透率较高的电网发生了频率跌落事故,如英国的“8.9”停电事故、澳大利亚南部电网解列事故,锦苏直流闭锁导致华东电网的频率跌落事故等[4]。
因此,文章首先从传统电力系统惯量运动方程及传统发电机的扰动动态过程出发探讨同步发电机的惯量支撑作用,进一步定性分析了新能源发电替代传统同步发电机后的系统惯量缺失机理,结合国内外的研究成果提出了电力系统惯量的简易评估指标和评估流程,并结合一个实际的省级电网2025-2060年的新能源发电投资和接入规划进行了惯量变化趋势的评估,为未来电力系统在扰动后的频率控制策略和功率调节规划提供指导建议。
-
对于传统电力系统,因扰动产生有功功率不平衡后,各同步发电机由于内电势相位和幅值不能突变,使得转子旋转过程中储存的动能会瞬时分担不平衡功率[9-11]。从能量守恒的角度,转子动能通过转子的加、减速过程转化为电磁功率,分担系统总的不平衡功率,从而保持与原动机输入机械功率一致,直至协同系统一、二次调频过程实现频率的稳定。此过程为传统同步机惯量响应过程,其实质反映的就是物理学中物体对运动状态变化的抵抗过程,因此利用惯量来衡量这一能力的大小[12-13]。
不考虑扰动瞬间产生的不同地区间的频率波动偏差,设频率为全系统一致,则扰动后系统的整体频率变化过程如式(1)所示[2]:
$$ 2\displaystyle \sum\limits_{i = 1}^N {{H_i}\dfrac{{{\mathrm{d}}\Delta f(t)}}{{{\mathrm{d}}t}}} = - \Delta {P_{\mathrm{d}}}(t) $$ (1) 式中:
$ \Delta {P_{\mathrm{d}}}(t) $ ——系统扰动所产生的不平衡功率,大于0表示出力突降或负荷突增,小于0表示负荷突降或出力突增;
$ \dfrac{{{\mathrm{d}}\Delta f(t)}}{{{\mathrm{d}}t}} $ ——t时刻的频率变化率;
Hi ——第i台发电机的惯性常数;
N ——同步发电机的台数。
式(1)中可以看到,对于扰动瞬间t0时刻,相同的功率扰动下,影响频率变化率的关键在于系统中的所有发电机的总惯量$ \displaystyle \sum\limits_{i = 1}^N {{H_i}} $。
-
定性分析可知,承担不平衡功率的机组数量越多,则系统频率稳定性越好。然而,由于新能源发电单元中大量采用电力电子接口接入系统,丧失了传统同步机通过转子动能承担扰动瞬间不平衡电磁功率的能力,而在后续频率控制过程中又由于新能源发电控制策略的特点,使其难以提供相应的支撑功率,因此式(1)中的N实质上变为了系统中传统同步机数目[14]。
因此,随着大量新能源发电对传统同步机出力的替代作用,系统中运行状态的同步机数目大幅度减少,增加了单台同步机分担的扰动功率,使得频率波动幅度增大。此外,当新能源发电单元在频率超预期下降过程中,由于控制策略或安全因素,可能导致集群新能源发电退出,进一步增大了不平衡功率,就可能导致频率崩溃事故[15]。
针对这一问题,通过逆变器控制策略来模拟同步机惯量响应特性的虚拟同步机技术(Virtual Synchronous Generator, VSG)成为研究热点,使得新能源发电单元也能够承担一定的惯量支撑能力[16-18]。此外,新能源电站配置的储能资源,也可以采用VSG技术提供惯量响应阶段的惯量支撑能力,但上述技术手段目前尚未得到广泛的工程应用,因此,目前电网规划和运行方式编制中涉及频率稳定性分析的工作中,对系统惯量支撑能力的评估通常也不考虑VSG提供的惯量支撑能力。
-
通常,利用惯性常数H来衡量传统机组的惯量大小,表达式如式(2)所示,为额定转速时机组转子动能与额定容量的比值,单位为s。
$$ H = \dfrac{{{E_{\mathrm{k}}}}}{{{S_{\mathrm{B}}}}} = \dfrac{{J\omega _{\mathrm{m}}^2}}{{2{S_{\mathrm{B}}}}} $$ (2) 由上式可知,在机组额定容量SB,机械角速度ωm不变的情况下,转子的转动惯量J、惯性常数H和机组动能Ek等价。
目前国内外描述大系统惯量水平使用较广泛的指标本质上是等价的[19-20],如系统总动能,系统惯性常数等。而评估高比例新能源接入系统惯量水平时,国内外往往使用更为简易的非同步发电瞬时渗透率(System Non-Synchronous Penetration)指标,即SNSP,见式(3):
$$ {R_{{\mathrm{SNSP}}}} = \dfrac{{{P_{{\mathrm{NG}}}} + {P_{{\mathrm{DC}}- {\mathrm{import}}}}}}{{{P_{\mathrm{L}}} + {P_{{\mathrm{export}}}}}}\times 100\text{%} $$ (3) 式中:
RSNSP ——系统非同步发电渗透率;
PNG ——本地新能源机组发电量;
PDC−import ——直流馈入本地的功率量;
PL ——本地负荷量;
Pexport ——本地送出功率。
若系统不含直流馈入,且不考虑新能源机组虚拟惯量,RSNSP与系统中新能源出力占运行机组总额定容量的比例相等,但在进行扰动后频率波动幅度的研究时,这一指标缺乏直观的物理意义,因此在考察大系统在稳定导则规定的扰动下维持频率稳定的能力时,更常见的评估指标为系统动能和系统惯性常数[14]。
对于含高比例新能源发电的系统来说,若不考虑新能源机组虚拟惯量,系统总动能计算如式(4)所示:
$$ {E_{\mathrm{k}}} = \displaystyle \sum\limits_{i = 1}^N {{H_{{\mathrm{G}}i}}{S_{ {\mathrm{G}}i}}} $$ (4) 式中:
Ek ——系统总动能(MW·s);
HGi、SGi ——第i台运行中同步发电机的惯性常数和额定容量;
N ——投运同步发电机的总数。
系统惯性常数为式(5)所示:
$$ {H_{{\mathrm{sys}}}} = \dfrac{{{E_{\mathrm{k}}}}}{{{S_{ {\mathrm{TB}}}}}} $$ (5) 式中:
Hsys ——系统惯性常数(s);
STB ——系统总发电容量(MW)。
-
不同的电力系统对惯性评估的要求是不同的。当系统规模比较稳定时,运行人员关注的是新能源出力替代比例提高后,系统惯量水平是否满足频率稳定的要求。此时,现有机组参数一般可通过实验获取,系统运行方式基本确定,因此可以获得较为准确的惯量水平。对于快速扩张的或规划态系统,由于缺乏准确的典型运行场景,且机组参数难以确定,故而规划和运行人员关注的是随着新能源出力比例增大时的系统惯量是否进入惯量偏小的敏感区。
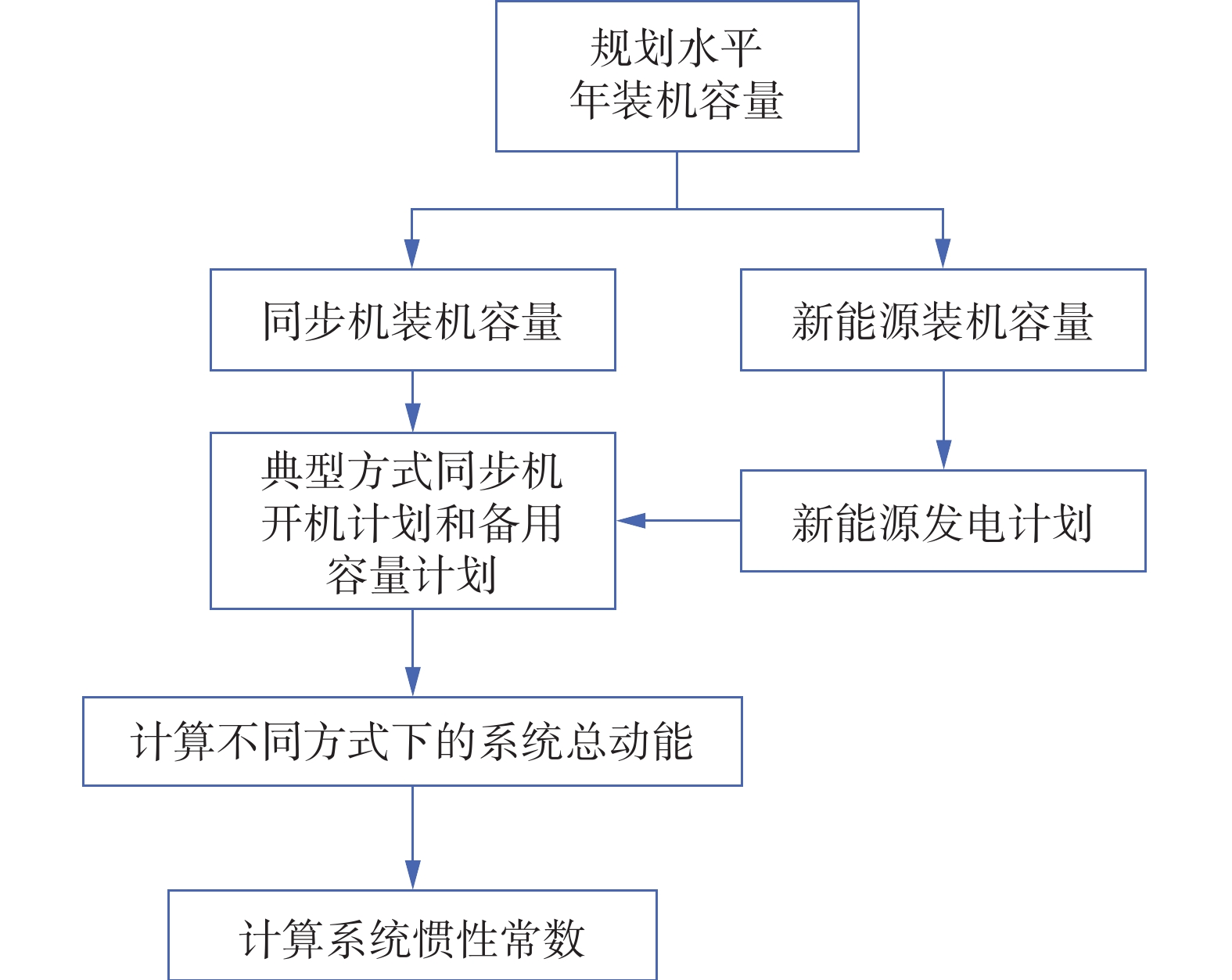
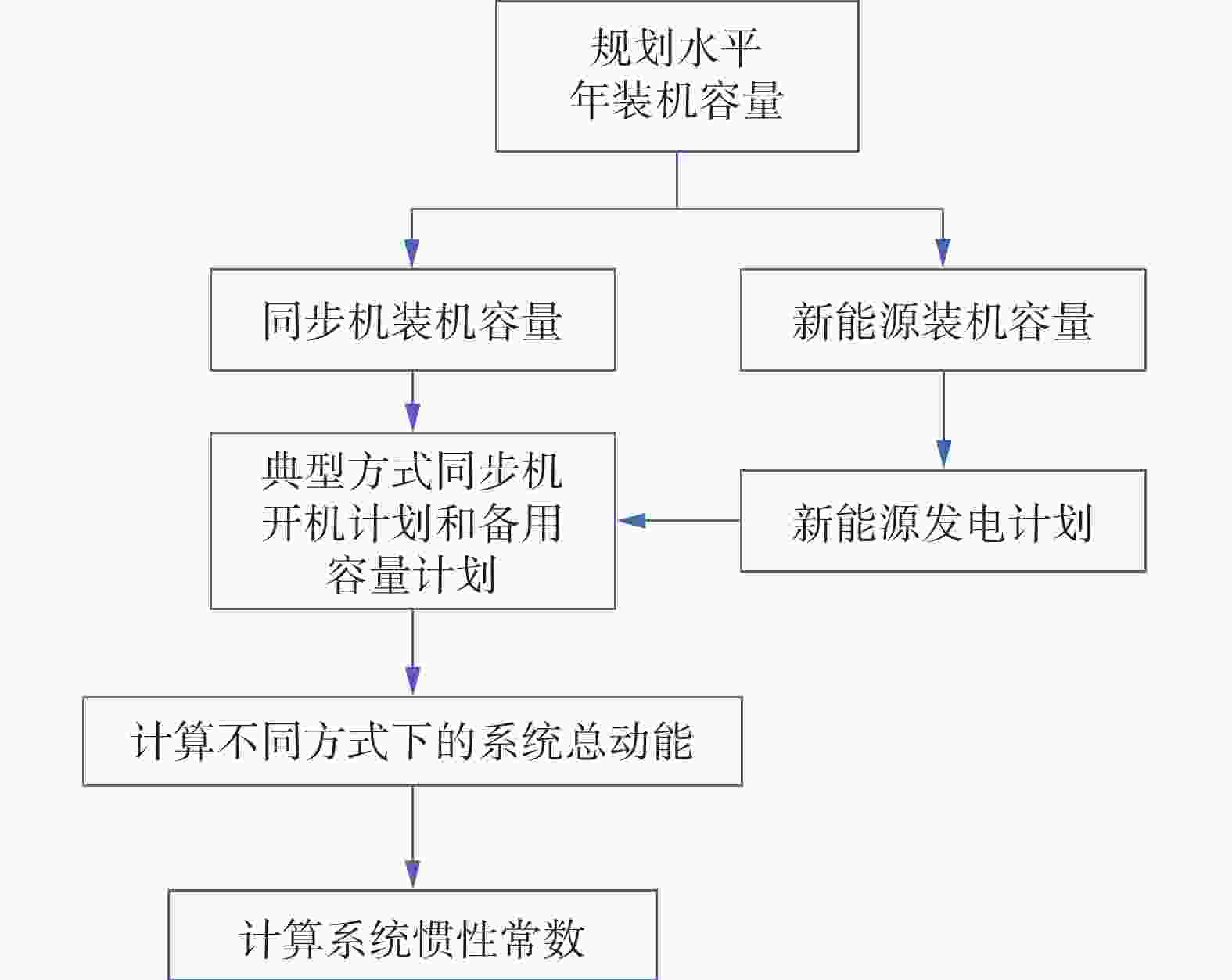
目前,虚拟惯量控制尚未广泛应用,系统总惯量可以看作只由同步机开机状态决定,因此基于新能源出力替代比例[7],利用系统规划和调峰计划方案的统计,可估计得到不同新能源出力比例下,不同运行方式下的同步机开机数目和机组总容量,从而根据机组平均惯性常数评估系统惯量范围。评估流程如图1所示。
Step 1:确定相应规划水平年待评估系统的总规模。
Step 2:基于规划方案计算同步机装机容量和新能源装机容量。
Step 3:根据调频调峰规划,估算不同典型运行方式同步机开机情况。
Step 4:根据式(4)计算总动能,出于数据获取的方便,可以根据不同类别机组的平均惯性常数估算系统的总动能。
Step 5:根据式(5)计算系统惯性常数。
需要注意的是,由于调频调峰方案的不确定性较大,使得Step 3中的同步机开机情况难以准确获得,因此对于规划态系统,往往只能评估其惯量水平的范围。
-
以某省级电网为研究对象,结合该省级电网的电源投资和开发情况,基于系统总动能和系统惯性常数指标对某省级电网2025-2060年间的惯量水平进行评估。
-
基础参数来自于该省级电网BPA数据,在此基础上进行适当简化。由于目前新能源发电尚未广泛应用虚拟惯量技术,因此风、光发电等新能源场站和外部直流馈入可以忽略其惯量支撑,因此在实际惯量估算中,仅考虑同步机惯量进行。
该省2025-2060年新能源和直流馈入工程的规划建设方案,如表1所示。
表 1 某省2025-2060年电源装机情况
Table 1. Installed capacity of power sources in a province from 2025 to
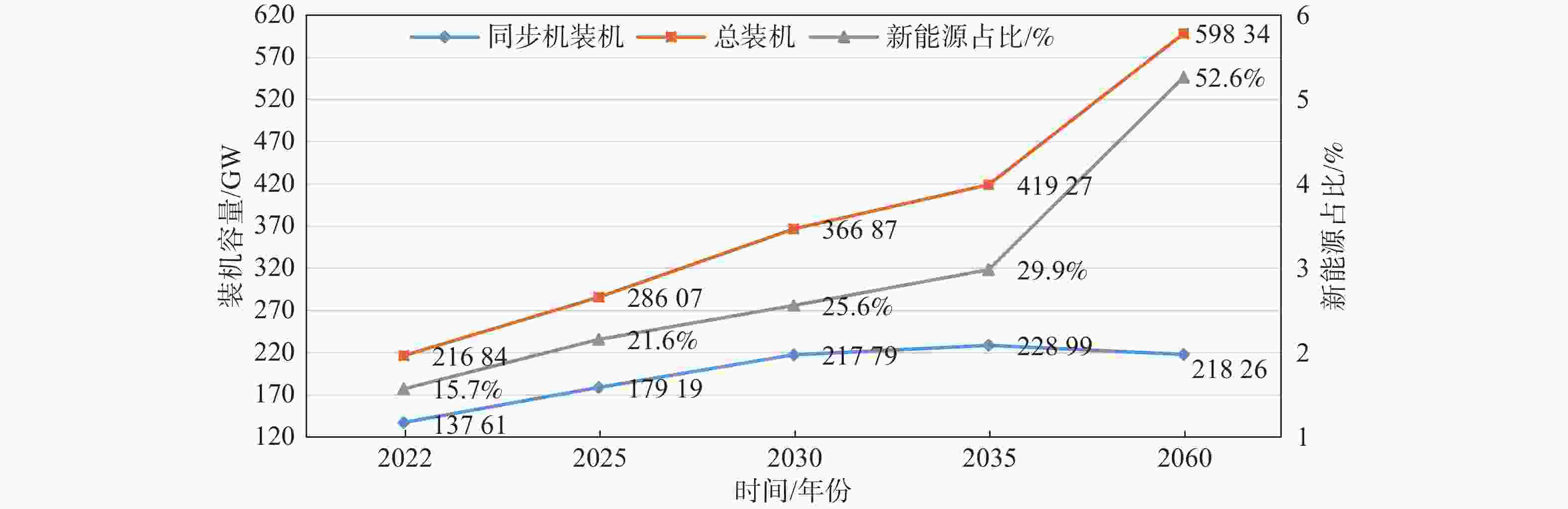
2060 电源类型 2025年 2030年 2035年 2060年 装机/GW 占比/% 装机/GW 占比/% 装机/GW 占比/% 装机/GW 占比/% 水电 9.26 3.24 9.26 2.52 9.26 2.21 9.26 1.55 抽水蓄能 9.68 3.38 15.88 4.33 22.08 5.27 40.00 6.69 煤电 91.12 31.85 99.12 27.02 99.12 23.64 64.00 10.70 气电 50.59 17.68 67.69 18.45 67.69 16.14 55.00 9.19 核电 18.54 6.48 25.84 7.04 30.84 7.36 50.00 8.36 新能源 58.80 20.55 88.00 23.99 117.20 27.95 295.00 49.30 储能 3.00 1.05 6.00 1.64 8.00 1.91 20.00 3.34 直流馈入 45.08 15.76 55.08 15.01 65.08 15.52 65.08 10.88 合计 286.07 100.00 366.87 100.00 419.27 100.00 598.34 100.00 从表1中可以看出,该省新能源及储能装机容量和比例逐年上升,到2035年左右达到30%,2060年渗透率超过50%,处于向高比例新能源系统的过渡期。从同步机总装机容量来看,该系统2035年之前一直处于增长期,而在2035年之后则进入下降周期。新能源比例、同步机容量及系统总容量的变化趋势,如图2所示。
-
基于该省实际数据调研,同步机平均惯性时间常数为10 s,因此对应的惯性常数H=TJ/2取为5 s。根据同步机装机容量,即表1中1~5行机组装机容量的总和,按照式(4)和式(5)测算其机组全开的总动能和惯性常数如表2所示。
表 2 某省电网2020-2035年总装机惯量水平评估
Table 2. Evaluation of total installed capacity and inertia level of a provincial power grid from 2020 to 2035
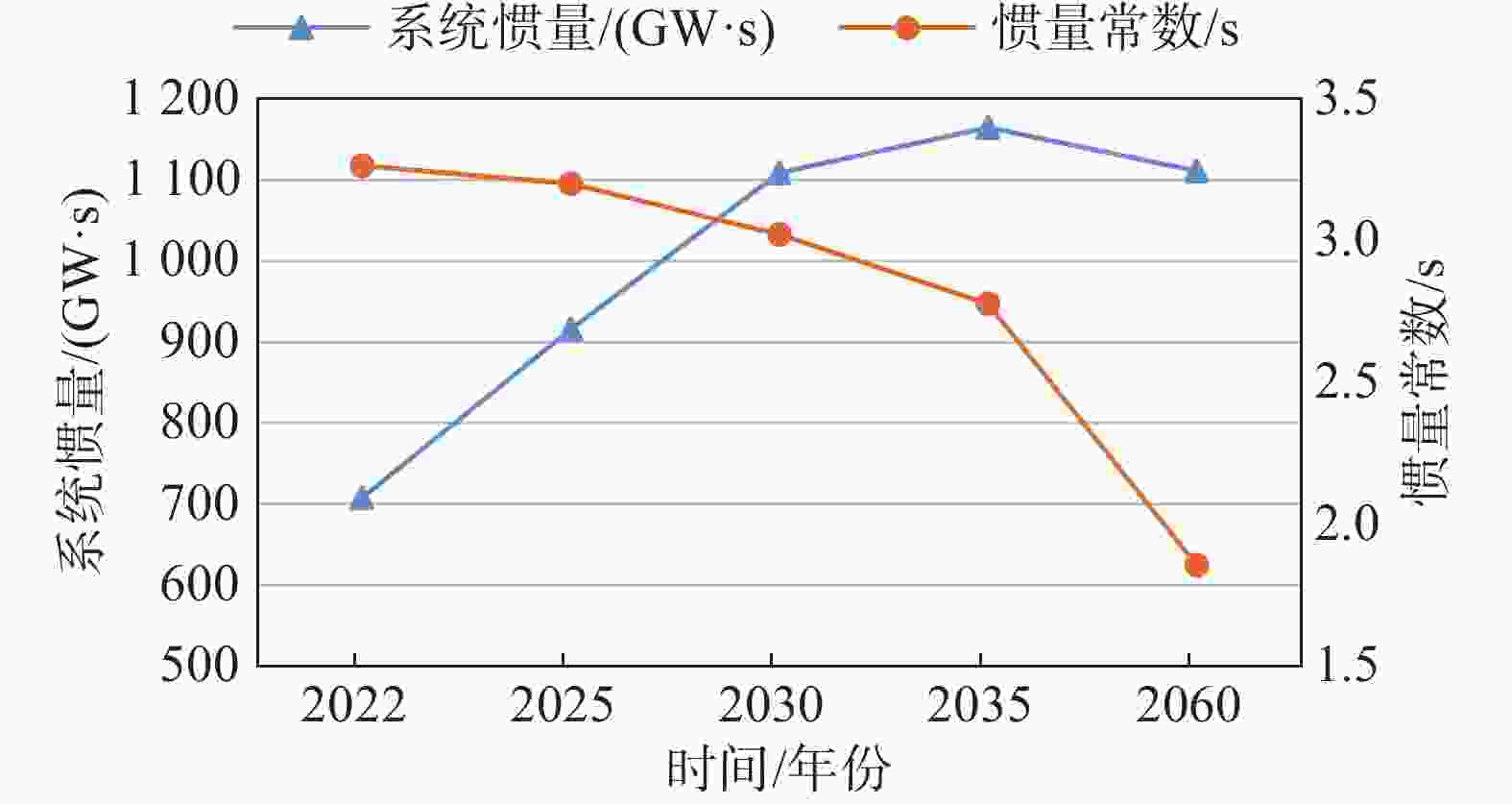
参数 2025年 2030年 2035年 2060年 装机容量/GW 286.07 366.87 419.27 598.34 系统惯量/(GW·s) 915.95 1 108.95 1 164.95 1 111.30 系统惯量常数/s 3.20 3.02 2.77 1.85 从系统装机容量角度进行的惯量水平评估可看出,虽然新能源装机容量在快速增大,但是由于2035年之前该系统同步机装机总容量仍然在逐年上升,因此系统惯量潜力在2035年之前也是逐步上升的,因此在同样的大扰动下系统的频率控制能够满足系统频率安全控制要求。
但是2035-2060年间,煤电、气电总计退出48 GW装机容量,而主要由风电、光伏出力及外省直流输电实现发电能力的替代,因此导致系统的整体惯量逐渐降低。同时系统规模扩大、新能源装机比例的提升,使得全系统惯量常数大幅度下降,如图3所示。依据文献[21]对主要电网惯量水平的测算及频率响应的仿真分析,当系统惯量常数低于3 s时,系统将进入惯量不足的状态,需要在规划过程中考虑惯量因素带来的备用比例和储备。
-
实际系统实时运行过程中惯量水平与系统同步机开机状况密切相关,因此对电网的惯量水平评估还要考虑实际运行方式下的新能源出力比例以及具备同步惯量的同步机、储能等支撑电源的投运状态。
由于未来风-光发电难以准确估算,因此风光发电的实际出力按照历史统计的风-光最高出力水平估算,结合发电时间的特征进行估算。通常该省最大负荷夏季日间出现,最小负荷冬季夜间出现,因此计算中不同类型电源出力设定为:最大负荷下,海上风电最大出力设定为装机容量65%,陆上风电设定为装机容量60%,光伏出力设定为装机容量80%,大发同时系数取0.8,其余负荷及旋转备用容量由同步机出力承担。最小负荷下,海上风电设定为装机容量的85%,陆上风电设定为装机容量的50%,光伏出力设为0,同时系数取0.8,其余负荷及旋转备用由同步机出力承担。根据该省2025-2035年旋转备用容量规划,设定了系统典型大、小方式下运行中的同步机出力,按照式(4)、式(5)估算了2025-2035年不同运行方式下的系统惯量和惯性常数。该省级电网2025-2035年典型运行方式惯量水平评估结果如表3所示。
表 3 该电网2025-2035年典型运行方式惯量水平评估
Table 3. Evaluation of inertia level for typical operation modes of the grid from 2025 to 2035
运行方式 参数 2025年 2030年 2035年 典型大方式 负荷/GW 184.00 207.09 221.09 同步机出力/GW 125.68 124.43 123.91 旋转备用/GW 10.80 12.18 13.02 外部直流/GW 38.00 48.00 48.00 新能源出力/GW 31.12 46.84 62.20 系统惯量/(GW·s) 628.40 622.15 619.55 系统惯量常数/s 3.42 3.00 2.80 典型小方式 负荷/GW 119.61 136.68 145.92 同步机出力/GW 95.97 96.08 93.54 新能源出力/GW 15.44 27.40 41.40 系统惯量/(GW·s) 479.85 480.40 467.70 系统惯量常数/s 4.01 3.51 3.21 从典型运行方式下该省电网惯量水平来看,在不考虑新能源机组惯量支撑能力时,系统的总体惯量常数在2030年之前不会低于3 s,但是2035年大方式下,由于新能源出力的替代明显,因此系统的总体惯性时间常数进入到新能源接入的敏感发展期。
结合系统的总体惯量指标来看,2030年前,无论是大方式还是小方式系统的总体惯量是在上升阶段,因此考虑到该省电网功率断面稳定性校核时断面功率缺额基本不变的场景,系统频率波动能够满足电网安全稳定运行要求。但是2030年后,随着系统规模的增大,系统的总体惯量反而逐渐下降,惯量常数下降趋势更为明显,会导致某些运行方式下惯量常数可能低于3 s,因此在运行方式安排过程中可以通过综合考虑同步机低负荷运行方式,以便更多的同步机容量进入备用,且限制直流线路的输电容量。
需要说明的是,这里的测算仅考虑了该电网本地电源及外来直流输电功率,但是由于整个大区电网内部结构相对紧密,耦合了外部水、火同步机电源后系统的惯量水平会进一步提升,因此整体来看,目前的同步机规模和备用容量能够满足该电网在2035年前的系统调频和惯量支撑的需求。
-
随着对惯量问题认识的深入以及装备技术的进步,配置储能的新能源场站参与惯量控制已经进入学者和从业专家的视野,并提出了不同的惯量支撑控制方案,其中,虚拟同步机控制技术(VSG)得到了广泛的关注。虚拟同步机就是通过电力电子接口的控制策略实现类似于同步机控制的接口,在系统扰动时提供虚拟惯量从而使得系统的惯量保持在合理的水平。目前,虚拟同步机技术的理论体系已基本成型,但是达到什么样的惯性支撑水平与系统的储能容量配置和运行过程中的SOC运行参数密切相关,在进行惯量水平评估时不宜设定过高。依据算例省份新能源场站的“10%装机容量运行1 h”的储能配置要求,假定VSG控制能够完全模拟储能装置等容量同步机的惯量响应,由于储能装置在SOC设定时通常考虑参与调频调峰运行,能够满足秒级时间尺度的惯量响应储能要求,因此在计算过程中新能源场站的惯量(场站总动能)设为同容量同步发电机惯量的1/10,则设定惯性常数H=0.5 s,按照式(4)和式(5)和表3中的同步机和新能源场站出力,重新估算该电网典型大、小运行方式下的总惯量水平和系统惯量常数,如表4所示。
表 4 计及新能源惯量支撑的电网惯量水平评估
Table 4. Evaluation of grid inertia level considering new energy inertia support
参数 2025年 2030年 2035年 典型大方式系统惯量/(GW·s) 643.96 645.57 650.65 典型大方式系统惯量常数/s 3.50 3.12 2.94 典型小方式系统惯量/(GW·s) 487.57 494.10 488.40 典型小方式系统惯量常数/s 4.08 3.62 3.35 从表4中可以看出,当新能源机组参与惯量支撑控制后,系统的总惯量水平有了较大提升,在2030年前,系统的整体惯性常数大于3 s,能够满足惯量支撑的需求。虽然2035年典型大方式下,系统惯量常数低于3 s,但注意式(4)中SGi的物理意义为运行中的同步机额定容量,而表4中的总动能是利用实际同步机出力计算而得到的。经测算,在运行方式安排中增加2.1 GW同步机装机容量处于运行状态即可使惯性常数提升至3 s,因此考虑只需部分机组的低负荷运行方式,使更多机组处于运行状态,即可保证2035年的惯量水平满足要求。
-
频率问题正在成为我国电力系统低碳化转型过程中所面临的重要挑战,高比例电力电子接口对电力系统有功频率控制的影响异常深远。不管是在发电端还是负荷端,越来越多电力电子接口设备的接入,对未来新型电力系统的频率稳定都会有愈发明显的影响。
本文分析了新能源通过电力电子接口接入电力系统后的惯量缺失机理,进一步讨论了评估电力系统惯量的常用指标和流程,并通过某省级电网2025-2060年的装机容量变化趋势,探讨了该电网与频率控制关系密切的系统总动能、系统惯性常数的发展趋势。评估结果表明基于当前规划方案,该系统在2035年之前惯量支撑能力充足,但是2035年之后,随着火电、气电机组退役规模快速增大,新能源出力替代的加速,系统开始呈现惯量水平不足的问题,需要着重在运行方式中考虑同步机的旋转备用及调峰容量,并通过部分机组的低负荷运行方式,保持并网同步发电机的总装机容量。此外,新能源的虚拟同步机控制策略的实用化进程,对于未来大规模新能源接入后的系统惯量支撑能力有极为重要的作用。
Mechanism of Inertia Loss and Evaluation of Inertia Level in Power Systems with Large Scale New Energy Access
-
摘要:
目的 为满足我国“30、60”的碳达峰、碳中和目标,大量风电、光伏等新能源发电通过变流器接口接入系统,以替代燃煤同步机组出力,极大地影响了电力系统惯量及相应的频率动态特性。 方法 首先分析传统电力系统惯量运动方程及传统发电机扰动后的惯量响应阶段的功频动态过程,再定性讨论了大规模新能源接入后的系统惯性缺失机理。 结果 讨论了国内外常用的集中惯性评价指标,阐述了用系统的总动能和惯性常数作为电网惯性评价指标的依据。 结论 结合某省级电网的新能源开发和消纳的规划,对该省级电网的惯量水平进行了工程化评估,提出了相应的惯量提升建议。 Abstract:Introduction In order to meet the national goals of "30·60" - peak carbon emissions by 2030 and achieving carbon neutrality by 2060 , an influx of new energy sources such as wind and photovoltaic power is integrated into the system via converter interfaces and progressively supplants coal-fired synchronous generators, significantly impacting the power system's inertia characteristics and the associated frequency dynamic characteristics.Method Firstly, the study reviewed the inertia equation of motion for traditional power systems, and the power-frequency dynamic process during the inertia response phase following a disturbance in traditional generators, and then qualitatively discussed the mechanism of system inertia loss due to the extensive integration of new energy sources. Result The study considers evaluation indicators used at home and abroad for broadly recognized centralized inertia, and elucidates the reason for employing the system's total kinetic energy and inertia constant as the inertia evaluation indicators for the power grid. Conclusion Combined with the planning of new energy development and consumption of a provincial power grid, an engineering evaluation of the grid's inertia level is carried out, and the corresponding suggestions for inertia improvement are put forward. -
Key words:
- new energy generation /
- power system inertia /
- frequency /
- inertia constant
-
表 1 某省2025-2060年电源装机情况
Tab. 1. Installed capacity of power sources in a province from 2025 to
2060 电源类型 2025年 2030年 2035年 2060年 装机/GW 占比/% 装机/GW 占比/% 装机/GW 占比/% 装机/GW 占比/% 水电 9.26 3.24 9.26 2.52 9.26 2.21 9.26 1.55 抽水蓄能 9.68 3.38 15.88 4.33 22.08 5.27 40.00 6.69 煤电 91.12 31.85 99.12 27.02 99.12 23.64 64.00 10.70 气电 50.59 17.68 67.69 18.45 67.69 16.14 55.00 9.19 核电 18.54 6.48 25.84 7.04 30.84 7.36 50.00 8.36 新能源 58.80 20.55 88.00 23.99 117.20 27.95 295.00 49.30 储能 3.00 1.05 6.00 1.64 8.00 1.91 20.00 3.34 直流馈入 45.08 15.76 55.08 15.01 65.08 15.52 65.08 10.88 合计 286.07 100.00 366.87 100.00 419.27 100.00 598.34 100.00 表 2 某省电网2020-2035年总装机惯量水平评估
Tab. 2. Evaluation of total installed capacity and inertia level of a provincial power grid from 2020 to 2035
参数 2025年 2030年 2035年 2060年 装机容量/GW 286.07 366.87 419.27 598.34 系统惯量/(GW·s) 915.95 1 108.95 1 164.95 1 111.30 系统惯量常数/s 3.20 3.02 2.77 1.85 表 3 该电网2025-2035年典型运行方式惯量水平评估
Tab. 3. Evaluation of inertia level for typical operation modes of the grid from 2025 to 2035
运行方式 参数 2025年 2030年 2035年 典型大方式 负荷/GW 184.00 207.09 221.09 同步机出力/GW 125.68 124.43 123.91 旋转备用/GW 10.80 12.18 13.02 外部直流/GW 38.00 48.00 48.00 新能源出力/GW 31.12 46.84 62.20 系统惯量/(GW·s) 628.40 622.15 619.55 系统惯量常数/s 3.42 3.00 2.80 典型小方式 负荷/GW 119.61 136.68 145.92 同步机出力/GW 95.97 96.08 93.54 新能源出力/GW 15.44 27.40 41.40 系统惯量/(GW·s) 479.85 480.40 467.70 系统惯量常数/s 4.01 3.51 3.21 表 4 计及新能源惯量支撑的电网惯量水平评估
Tab. 4. Evaluation of grid inertia level considering new energy inertia support
参数 2025年 2030年 2035年 典型大方式系统惯量/(GW·s) 643.96 645.57 650.65 典型大方式系统惯量常数/s 3.50 3.12 2.94 典型小方式系统惯量/(GW·s) 487.57 494.10 488.40 典型小方式系统惯量常数/s 4.08 3.62 3.35 -
[1] 孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究 [J]. 中国电机工程学报, 2020, 40(16): 5179-5191. DOI: 10.13334/j.0258-8013.pcsee.200493. SUN H D, WANG B C, LI W F, et al. Research on inertia system of frequency response for power system with high penetration electronics [J]. Proceedings of the CSEE, 2020, 40(16): 5179-5191. DOI: 10.13334/j.0258-8013.pcsee.200493. [2] 张子扬, 张宁, 杜尔顺, 等. 双高电力系统频率安全问题评述及其应对措施 [J]. 中国电机工程学报, 2022, 42(1): 1-24. DOI: 10.13334/j.0258-8013.pcsee.211425. ZHANG Z Y, ZHANG N, DU E S, et al. Review and countermeasures on frequency security issues of power systems with high shares of renewables and power electronics [J]. Proceedings of the CSEE, 2022, 42(1): 1-24. DOI: 10.13334/j.0258-8013.pcsee.211425. [3] 陈国平, 李明节, 许涛, 等. 关于新能源发展的技术瓶颈研究 [J]. 中国电机工程学报, 2017, 37(1): 20-26. DOI: 10.13334/j.0258-8013.pcsee.161892. CHEN G P, LI M J, XU T, et al. Study on technical bottleneck of new energy development [J]. Proceedings of the CSEE, 2017, 37(1): 20-26. DOI: 10.13334/j.0258-8013.pcsee.161892. [4] 秦晓辉, 苏丽宁, 迟永宁, 等. 大电网中虚拟同步发电机惯量支撑与一次调频功能定位辨析 [J]. 电力系统自动化, 2018, 42(9): 36-43. DOI: 10.7500/AEPS20171122007. QIN X H, SU L N, CHI Y N, et al. Functional orientation discrimination of inertia support and primary frequency regulation of virtual synchronous generator in large power grid [J]. Automation of electric power systems, 2018, 42(9): 36-43. DOI: 10.7500/AEPS20171122007. [5] 鲁宗相, 汤海雁, 乔颖, 等. 电力电子接口对电力系统频率控制的影响综述 [J]. 中国电力, 2018, 51(1): 51-58. DOI: 10.11930/j.issn.1004-9649.201711236. LU Z X, TANG H Y, QIAO Y, et al. The impact of power electronics interfaces on power system frequency control: a review [J]. Electric power, 2018, 51(1): 51-58. DOI: 10.11930/j.issn.1004-9649.201711236. [6] 申家锴, 李卫东, 李正文, 等. 计及一次调频死区与限幅的高比例风电电力系统机组组合 [J]. 电网技术, 2022, 46(4): 1326-1334. DOI: 10.13335/j.1000-3673.pst.2021.2283. SHEN J K, LI W D, LI Z W, et al. Unit commitment of power system with high proportion of wind power considering the deadband and limiter of primary frequency response [J]. Power system technology, 2022, 46(4): 1326-1334. DOI: 10.13335/j.1000-3673.pst.2021.2283. [7] 张谦, 周林, 周雒维, 等. 计及电动汽车充放电静态频率特性的负荷频率控制 [J]. 电力系统自动化, 2014, 38(16): 74-80. DOI: 10.7500/AEPS20131210005. ZHANG Q, ZHOU L, ZHOU L W, et al. Load frequency control considering charging and discharging static frequency characteristics of electric vehicles [J]. Automation of electric power systems, 2014, 38(16): 74-80. DOI: 10.7500/AEPS20131210005. [8] O'SULLIVAN J, ROGERS A, FLYNN D, et al. Studying the maximum instantaneous non-synchronous generation in an island system-frequency stability challenges in Ireland [J]. IEEE transactions on power systems, 2014, 29(6): 2943-2951. DOI: 10.1109/TPWRS.2014.2316974. [9] 安琪. 新形势下构建能源技术创新体系思路与措施 [J]. 中国能源, 2020, 42(11): 40-43. DOI: 10.3969/j.issn.1003-2355.2020.11.009. AN Q. Policy frame and measures for constructing an energy technology innovation system under the new situation [J]. Energy of China, 2020, 42(11): 40-43. DOI: 10.3969/j.issn.1003-2355.2020.11.009. [10] 康重庆, 姚良忠. 高比例可再生能源电力系统的关键科学问题与理论研究框架 [J]. 电力系统自动化, 2017, 41(9): 2-11. DOI: 10.7500/AEPS20170120004. KANG C Q, YAO L Z. Key scientific issues and theoretical research framework for power systems with high proportion of renewable energy [J]. Automation of electric power systems, 2017, 41(9): 2-11. DOI: 10.7500/AEPS20170120004. [11] 中国电力企业联合会. 中国电力行业年度发展报告2020 [M]. 北京: 中国建材工业出版社, 2020. China Electricity Council. Annual development report of China's power industry [M]. Beijing: China Building Materials Press, 2020. [12] 国家发展和改革委员会能源研究所. 中国2050高比例可再生能源发展情景暨路径研究 [R]. 北京: 国家发展和改革委员会能源研究所, 2015. Energy Research Institute of the National Development and Reform Commission. China 2050 high renewable energy penetration scenario and roadmap study [R]. Beijing: Energy Research Institute of the National Development and Reform Commission, 2015. [13] 谭雪, 刘俊, 郑宽, 等. 新一轮能源革命下中国电网发展趋势和定位分析 [J]. 中国电力, 2018, 51(8): 49-55. DOI: 10.11930/j.issn.1004-9649.201805061. TAN X, LIU J, ZHENG K, et al. Research on tendency and positioning of power grid development in the new round energy revolution [J]. Electric power, 2018, 51(8): 49-55. DOI: 10.11930/j.issn.1004-9649.201805061. [14] 任凯奇, 张东英, 黄越辉, 等. 基于新能源出力比例的大规模系统惯量估计 [J]. 电网技术, 2022, 46(4): 1307-1315. DOI: 10.13335/j.1000-3673.pst.2021.0643. REN K Q, ZHANG D Y, HUANG Y H, et al. Large-scale system inertia estimation based on new energy output ratio [J]. Power system technology, 2022, 46(4): 1307-1315. DOI: 10.13335/j.1000-3673.pst.2021.0643. [15] GUERRERO J M, VASQUEZ J C, MATAS J, et al. Hierarchical control of droop-controlled AC and DC microgrids-A general approach toward standardization [J]. IEEE transactions on industrial electronics, 2011, 58(1): 158-172. DOI: 10.1109/TIE.2010.2066534. [16] ZHONG Q C, WEISS G. Synchronverters: inverters that mimic synchronous generators [J]. IEEE transactions on industrial electronics, 2011, 58(4): 1259-1267. DOI: 10.1109/TIE.2010.2048839. [17] 李清, 陈斌, 徐志华, 等. 虚拟同步发电机及其在混合微电网中的应用 [J]. 电力电子技术, 2018, 52(4): 27-30. LI Q, CHEN B, XU Z H, et al. VSG technology and its application in hybrid micro-grid [J]. Power electronics, 2018, 52(4): 27-30. [18] ZHANG W Y, CANTARELLAS A M, ROCABERT J, et al. Synchronous power controller with flexible droop characteristics for renewable power generation systems [J]. IEEE transactions on sustainable energy, 2016, 7(4): 1572-1582. DOI: 10.1109/TSTE.2016.2565059. [19] ASHABANI M, FREIJEDO F D, GOLESTAN S, et al. Inducverters: PLL-less converters with auto-synchronization and emulated inertia capability [J]. IEEE transactions on smart grid, 2016, 7(3): 1660-1674. DOI: 10.1109/TSG.2015.2468600. [20] BLAABJERG F, TEODORESCU R, LISERRE M, et al. Overview of control and grid synchronization for distributed power generation systems [J]. IEEE transactions on industrial electronics, 2006, 53(5): 1398-1409. DOI: 10.1109/TIE.2006.881997. [21] 曹炜, 张甜, 傅业盛, 等. 同步调相机增强电力系统惯性和改善频率响应的研究与应用 [J]. 电力系统自动化, 2020, 44(3): 1-10. DOI: 10.7500/AEPS20190429015. CAO W, ZHANG T, FU Y S, et al. Research and application for increasing inertia and improving frequency response of power system by using synchronous condenser [J]. Automation of electric power systems, 2020, 44(3): 1-10. DOI: 10.7500/AEPS20190429015. -




 下载:
下载: