-
区域综合能源系统（RIES）在提高社会能源利用效率、促进可再生能源规模化开发、保证能源供应安全、实现中国节能减排与碳中和目标等方面具有重要意义[1-3]。而RIES的多能流耦合特性决定了系统在设计和运行中需要同时面临来自供能侧和用户侧的问题[4-5]。随着智能电网的发展和能源市场化改革进一步推进，用户侧也被积极鼓励参与到能源系统优化中[6-7]。在RIES中实施需求响应是传统电力系统需求响应在RIES中的进一步延伸与拓展，强调电[8-9]、热[10-11]等多类型灵活性负荷资源的协同管理，进一步丰富了用户的响应方式与响应潜力。
为了降低系统运行成本、提高能源利用效率、减少弃风弃光现象，越来越多的国内外学者将需求响应机制引入到RIES中，从经济效益、系统能效和可再生能源消纳等角度研究了考虑需求响应的RIES经济运行与优化调度。文献[12]建立了综合考虑价格型需求响应和激励性需求响应的RIES容量配置优化模型，案例证明了需求响应使得系统和用户在经济效益上达到了双赢。文献[13]在考虑碳排放权交易方案和大气污染控制要求的基础上引入价格型需求响应机制，建立了考虑RIES的环境效益和经济成本的多目标优化模型。文献[14]以电价和热价作为需求响应信号引导终端用户参与需求响应，算例结果表明电热负荷参与需求响应可有效降低RIES的总运行成本，提高了光热资源的利用率。文献[15]基于碳交易阶梯型奖惩机制和电-热-气需求响应模式，建立以总成本最低为目标的氢能综合能源系统低碳运行优化模型，实现了RIES经济、低碳、高效运行。文献[16]将需求响应和碳捕集设备整合为电力等效虚拟储能，并参与电力系统削峰填谷，提高了RIES经济性和风能利用率。文献[17]在用户侧引入传统需求响应策略，并与生产侧的热电联供实现耦合，在提高系统经济性和清洁性的同时，使生产侧设备出力更加灵活可靠。文献[18]在RIES中需求响应和引入阶梯式碳交易机制，并建立生命周期评估方法构建以碳交易成本、购能成本和弃风成本之和最小为目标的运行优化模型，大幅度的提升了系统清洁性和运行灵活性。文献[19]分析各类型综合需求响应的多时间尺度特性，根据用户用能特征制定了对应的需求响应策略和以经济性最优为目标的RIES运行优化模型，充分发挥了供能设备的日内调度潜力。文献[20]根据不同时间尺度，设计了一种基于氢储能和需求响应的RIES双层框架，可以在减少用户用能成本，增加新能源消纳率的同时，降低供能设备功率失衡风险。文献[21]通过对用户用能行为进行需求响应的精细化建模，提出一种考虑需求响应的综合能源系统日前优化调度方法。案例结果表明需求响应可以优化用户负荷曲线，提高综合能源系统的经济性和运行能效。
综上所述，需求响应能有效降低系统运行成本，促进绿色能源消纳，改善能源调峰体系，是一种可行的灵活性负荷资源管理手段。然而现有研究往往聚焦于电、热负荷等方面，需求响应数学模型不够精确，并且缺少对冷负荷在内的多种灵活性负荷的整体研究。同时在评价体系的构建上，现有模型大多以系统供能侧运行成本为目标函数，未能兼顾供能侧与用户侧的经济利益，减弱了供需双方之间灵活性负荷资源统一配置的能力和协同优化的潜力。同时在评价体系的构建上，现有模型大多以系统供能侧运行成本为目标函数，未能兼顾供能侧与用户侧双方的经济效益，影响系统供需双方间的交互作用和协同优化潜力。
为了解决上述问题，文章根据不同用户的用能特点和需求响应潜力，将参与需求响应的灵活性负荷资源划分为可平移负荷、可调度负荷以及可削减负荷，对应不同的需求响应策略。然后基于RIES中多种异质能流的耦合特性和用户侧灵活性负荷的响应潜力，以供需双方的经济效益、电负荷峰谷比以及碳排放量等综合评价指标最优为目标函数，建立了考虑冷热电灵活性需求响应的RIES运行优化模型，并将其分为用户侧需求响应模块和供能侧能量流动模块，以实现能源系统供能侧和用户侧协同优化。最后选取中国广州某工业园区进行案例分析，得到负荷需求响应方案和各能源网络的优化结果，并通过对比需求响应前后各评价指标，从而验证所建模型的合理性和实用性。
-
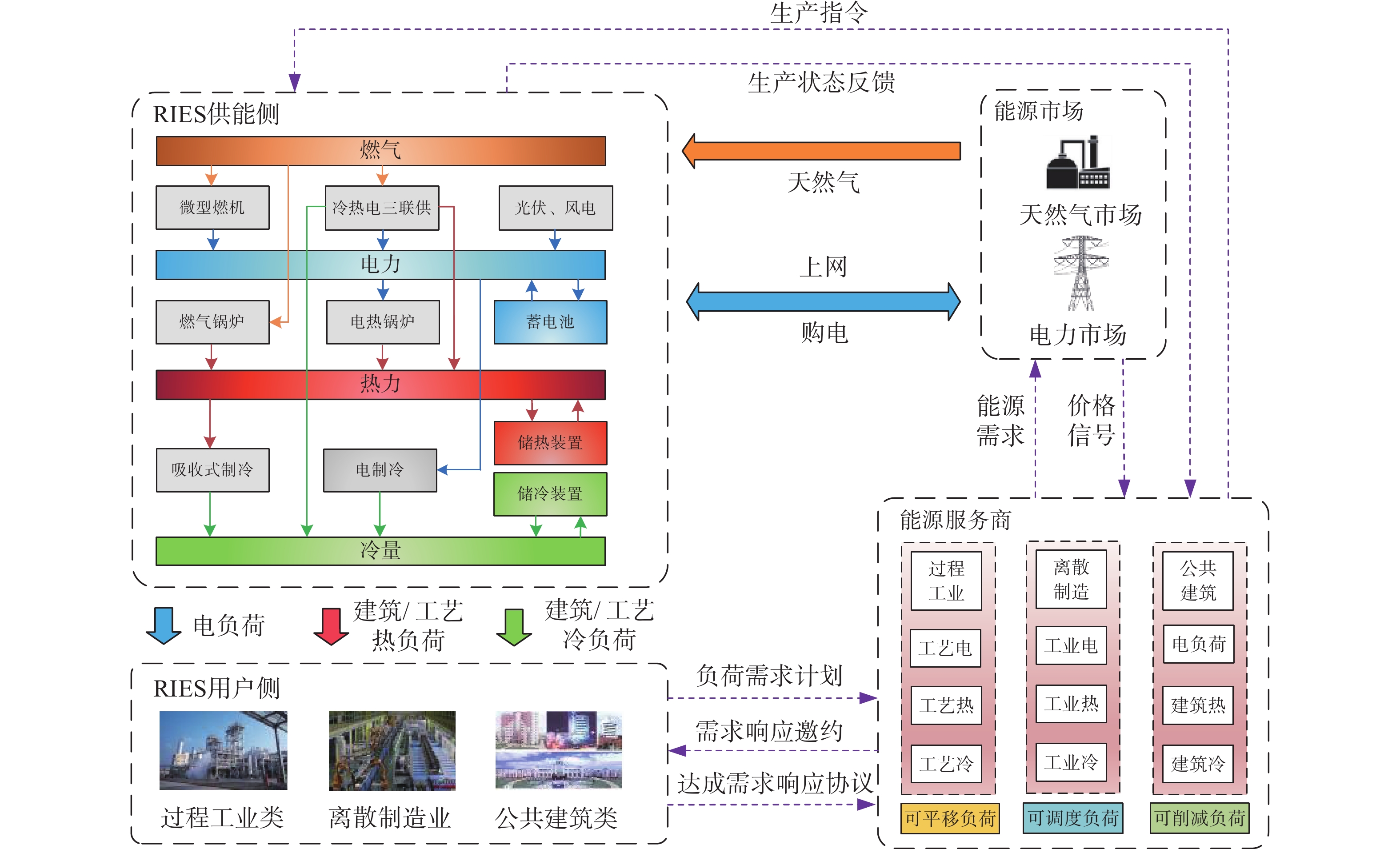
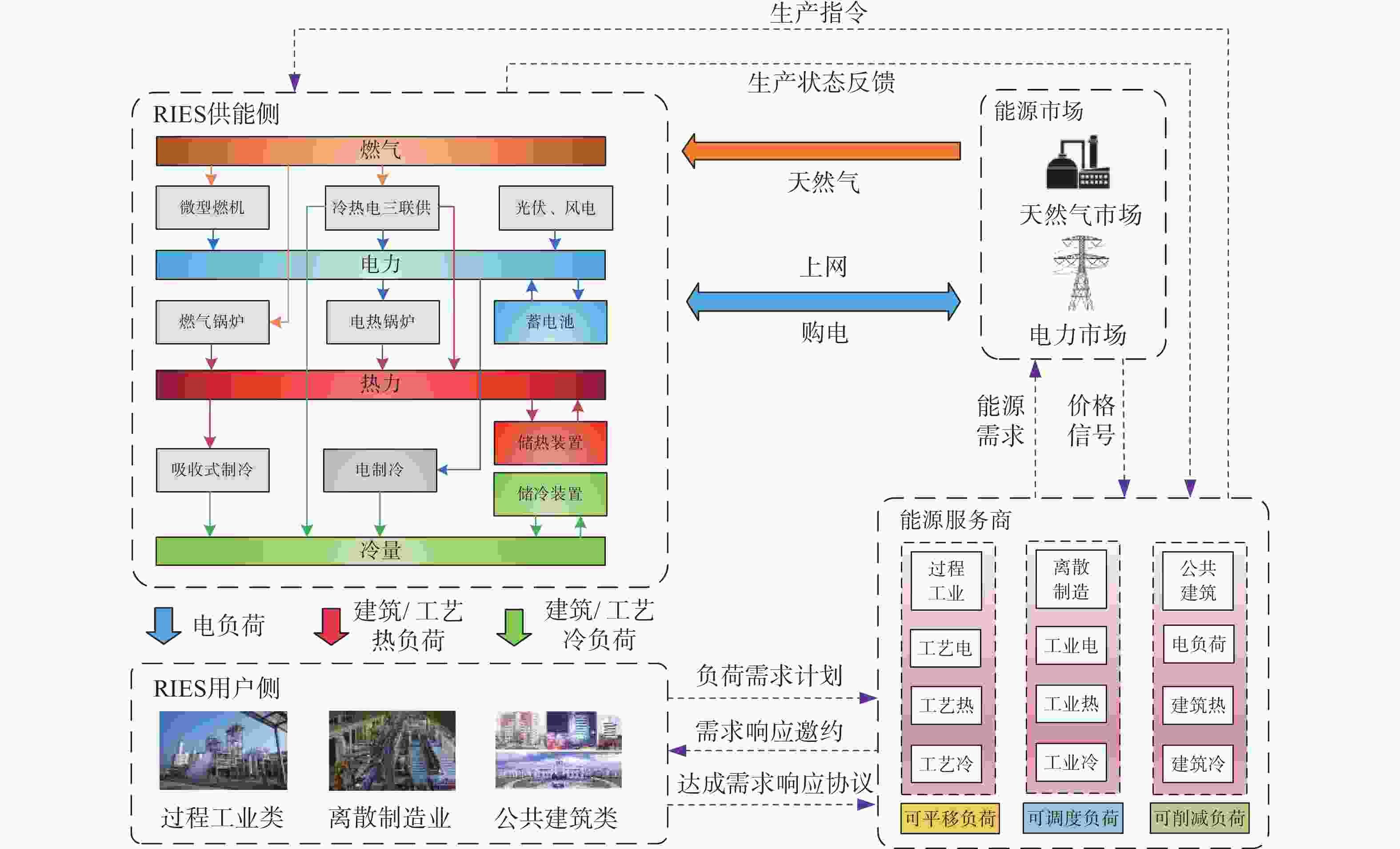
RIES以CCHP机组为核心，将原有独立的天然气系统、电力系统、热力系统和供冷系统相耦合，扩大了可再生能源的消费空间，可为用户提供冷、热、电、汽等多种形式的能量[22-24]，因此RIES设备种类繁多，运行特性复杂。文章提出的RIES需求响应机制结构框架如图1所示，首先，用户将冷热电负荷需求整合为负荷需求计划上报给能源服务商；其次，能源服务商根据能源市场反馈的市场价格信号或负荷需求计划，决定系统需要实施需求响应，则对用户发出需求响应邀约；然后，能源服务商和用户经过协商决定参与需求响应的用户类型和对应的冷热电灵活性负荷量、需求响应经济补偿机制，并形成需求响应协议；最后，能源服务商基于需求响应协议向RIES供能侧发出生产指令，让RIES个能源设备稳定、高效地供能。
图 1 RIES需求响应机制结构框架
Figure 1. Structure of RIES demand response mechanism
-
选择能源供给侧和用户侧的经济效益，电力负荷峰谷比和碳排放量作为评价指标，以充分发挥需求响应在提高系统经济效益和节能减排的优势。在权衡各评价指标的重要性后，目标函数F由各评价指标与其相应权重系数的乘积之和构成如式（1）所示：
$$ \min F = {f_1}\frac{{{C_{{\text{t,A}}}}}}{{{C_{{\text{t,B}}}}}} + {f_2}\frac{{{C_{{\text{d,A}}}}}}{{{C_{{\text{d,B}}}}}} + {f_3}\frac{{{\mathrm{C}}{{\mathrm{E}}_{\text{A}}}}}{{{\mathrm{C}}{{\mathrm{E}}_{\text{B}}}}} + {f_4}\frac{{{\mathrm{EL}}{{\mathrm{R}}_{\text{A}}}}}{{{\mathrm{EL}}{{\mathrm{R}}_{\text{B}}}}} $$ (1) 式中：
$ {C_{{\text{t,B}}}} $、$ {C_{{\text{t,A}}}} $ ——响应前后RIES的年总成本（元）；
$ {C_{{\text{d,B}}}} $、$ {C_{{\text{d,A}}}} $ ——响应前后用户的年能源交易成本（元）；
$ {\mathrm{C}}{{\mathrm{E}}_{\text{B}}} $、$ {\mathrm{C}}{{\mathrm{E}}_{\text{A}}} $ ——响应前后RIES的年碳排放量（t）；
$ {\mathrm{EL}}{{\mathrm{R}}_{\text{B}}} $、$ {\mathrm{EL}}{{\mathrm{R}}_{\text{A}}} $ ——响应前后RIES的电负荷峰谷比；
${f_1}$、$ {f_2} $、$ {f_3} $、$ {f_4} $ ——各评价指标的权重。
上式（1）中
$$ {C_{\text{t}}} = {C_{{\text{inv}}}} + {C_{\text{o}}} + {C_{\text{m}}} + {C_{\text{e}}} $$ (2) $$ {C_{{\text{inv}}}} = \frac{{I{{\left( {1 + I} \right)}^N}}}{{{{\left( {1 + I} \right)}^N} - 1}}\left( {\mathop \sum \limits_j {\mathrm{CA}}{{\mathrm{P}}_j} \cdot {\mathrm{IN}}{{\mathrm{V}}_j}} \right) $$ (3) $$ {C_{\text{o}}} = \mathop \sum \limits_i \left( {{C_{{\text{ng}},i}} \cdot {G_{{\text{ng}},i}} + {C_{{\text{e}},i}} \cdot {E_{{\text{e}},i}} - {C_{{\text{sell}},i}} \cdot {E_{{\text{sell}},i}}} \right) $$ (4) $$ {C_{\text{m}}} = \mathop \sum \limits_i \left( {\mathop \sum \limits_j {P_{j,i}} M_j} \right) \Delta T $$ (5) $$ {C_{\text{d}}} = {C_{{\text{trade}}}} - {C_{\text{e}}} $$ (6) $$ C_\text{E} = \mathop \sum \limits_i \left( {{G_{{\text{ng}},i}} {\rho _{{\text{ng}}}} + {E_{{\text{e}},i}} {\rho _{\text{e}}}} \right) $$ (7) $$ {\mathrm{ELR}} = {\text{max}}\left( {{\mathrm{EL}}} \right)/{\text{min}}\left( {{\mathrm{EL}}} \right) $$ (8) 式中：
$ {C_{{\text{inv}}}} $、${C_{\text{o}}}$、${C_{\text{m}}}$——能源系统的年投资成本、年运行成本及年维护成本（元）；
${C_{\text{e}\;}}$ ——能源系统对用户参与需求响应的经济补偿（元）；
$ C_{{\mathrm{trade}}} $ ——用户购买能源的成本（元）；
$C_{\mathrm{E}}$ ——用户购买能源的成本（元）；
I ——折旧率；
N ——机组的使用年限，（年）；
$ {{{\mathrm{CAP}}}}_{{j}} $、$ {{{\mathrm{INV}}}}_{{j}} $ ——设备j的额定容量与单位投资成本，（元）；
$ {{G}}_{\mathrm{n}\mathrm{g},{i}} $、$ {{E}}_{\mathrm{e},{i}} $ ——i时刻天然气与电的消耗量（m3、kWh）；
$ {{C}}_{\mathrm{n}\mathrm{g},{i}\;} $、$ {{C}}_{\mathrm{e},{i}} $ ——i时刻的天然气价与电价（元/m3、元/kWh）；
$ {{C}}_{\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{l},{i}} $、$ {{E}}_{\mathrm{s}\mathrm{e}\mathrm{l}\mathrm{l},{i}} $ ——i时刻的上网电价与上网电量（元/kWh、kWh）；
$ {{P}}_{{j},{i}\;} $ ——i时刻设备j的出功（kWh）；
$ {{M}}_{{j}} $ ——设备j的单位维护成本（元/年）；
$ {\mathrm{\rho }}_{\mathrm{n}\mathrm{g}} $、$ {\mathrm{\rho }}_{\mathrm{e}} $ ——天然气与网电的CO2排放因子（t/m3、t/kWh）；
$ {\mathrm{EL}} $ ——运行日电负荷（kWh）。
-
根据能源需求响应潜力和用户用能特性的不同，参与需求响应的用户侧冷热电灵活性负荷可分为可平移负荷、可调度负荷和可削减负荷，对应不同的响应策略。因此，用户侧需求响应模型分为可平移负荷模型、可调度负荷模型和可削减负荷模型。此外，还需建立需求响应的经济补偿模型，研究需求响应对供给侧和用户侧经济性的影响。
-
由于食品厂、医药厂等过程工业类用户通常是持续生产，不能将原本的工程流程拆分开来，违背实际用能方式，因此可平移负荷不能以1 h为单位进行需求响应，而是具体通过调整过程工业类用户相关生产工序，或改变生产班制，将原本在用能高峰期的某几个小时的生产负荷整体转移到用能压力较小时段的相同时长内，从而实现工艺负荷的整体平移。过程工业类用户工艺用电负荷平移如式（9）所示。
$$ {D}_{\text{tran}}^{\text{pe}} = {D}_{\text{o}}^{\text{pe}}\text{ } {\displaystyle \sum }_{j=1}^{24}{X}_{i,j} $$ (9) 式中：
$ D_{{\text{tran}}}^{{\text{pe}}} $ ——过程工业类用户电负荷平移后的负荷时序，是形式为[0, 0, 0, e1, e2, e3, … , en, 0, 0, 0]的1×24矩阵，且e1=e2=…= en=1；
$ {X_{i,j}} $ ——负荷平移的自变量，形式为[0, 0, 0, 0, 1, 0, 0, …]T，且该变量中只有一个1，代表负荷平移小时数；
$ D_{\text{o}}^{{\text{pe}}} $ ——原始的负荷时序。
过程工业类用户的工艺冷、热负荷随该生产流程内的电负荷参与需求响应，如式（10）所示。
$$ D_{{\text{tran}}}^{{\text{pc}}} = D_{{\text{tran}}}^{{\text{ph}}} = D_{{\text{tran}}}^{{\text{pe}}} $$ (10) 式中：
$ D_{{\text{tran}}}^{{\text{pc}}} $、$D_{{\text{tran}}}^{{\text{ph}}}$ ——过程工业类用户工艺冷负荷与工艺热负荷平移后的负荷时序。
工业用户参与需求响应后的负荷需求量如式（11）所示。
$$ U_{{\text{tran}},i}^m = D_{{\text{tran}}}^m U_{{\text{pro}},i}^m + U_{{\text{o}},i}^m $$ (11) 式中：
$U_{{\text{tran}},i}^m$、$U_{{\text{pro}},i}^m$、$U_{{\text{o}},i}^m$ ——过程工业用户i时刻m类负荷平移后的负荷需求量（kWh），m类可平移的负荷需求量（kWh）和m类不可平移负荷需求量（kwh），$ m \in \{ {\text{pe,ph,pc}}\} $，pe代表用电负荷、ph代表用热负荷、pc代表用冷负荷。
-
提出的可调度负荷模型是将离散制造类用户（如电子设备厂、 汽车制造厂等）在用能高峰段内某几个小时的灵活性负荷资源集中分配到用能压力较小时段的某一个小时内。参与需求响应后，用户在i时刻的$ n $类负荷总需求量如式（12）所示。
$$ {U}_{\text{disp},i}^{n}=\text{ }{U}_{\text{o},i}^{n}+{\sigma }_{\text{a},i}{U}_{\text{a},i}^{n}-{\sigma }_{\text{s},i}{U}_{\text{s},i}^{n} $$ (12) 式中：
$U_{{\text{disp}},i}^n$、$U_{{\text{o}},i}^n$ ——公共类用户i时刻n类负荷调度后和原有的负荷需求量（kWh）；
${\sigma _{{\text{a}},i}}$、${\sigma _{{\text{s}},i}}$ ——$ n $类负荷i时刻接收和转出的状态，为0-1变量；
$U_{{\text{a}},i}^n$、$U_{{\text{s}},i}^n$ ——用户i时刻可接收和可转出的n类可调度负荷量（kWh），$ n \in \{ {\text{de,\;dh,\;dc}}\} $，de代表工业用电，dh代表工业用热、dc代表工业用冷。
逐时负荷调度量不能大于可调度负荷转出或接收的总量，因此需满足以下约束：
$$ U_{{\text{s}},i}^n \leqslant U_{{\text{s}},i}^{n,{\text{t}}} $$ (13) $$ U_{{\text{a}},i}^n \leqslant U_{{\text{a}},i}^{n,{\text{t}}} $$ (14) 式中：
$U_{{\text{s}},i}^{n,{\text{t}}}$、$U_{{\text{a}},i}^{n,{\text{t}}}$ ——用户i时刻可转出和可接收的n类可调度负荷总量（kWh、kWh）。
可调度负荷在全天内的转出和接受的总量应当相等，如式（15）所示。此外， 任意时刻的可调度负荷只能存在转出和接受中的一种工作状态，如式（16）所示。
$$ \sum {\sigma _{{\text{s}},i}U_{{\text{s}},i}^n} - \sum{} {\sigma _{{\text{a}},i}}U_{{\text{a}},i}^n = 0 $$ (15) $$ {\sigma _{{\text{s}},i}} {\sigma _{{\text{a}},i}} = 0 $$ (16) -
由建立的可平移负荷和可调度负荷的数学模型可知，上述两种负荷参与需求响应前后负荷总量保持不变。而可削减负荷则是在负荷高峰时段内直接削减用户负荷，改变负荷曲线。相较于过程工业类和离散制造业类用户的负荷总量和生产息息相关，难以直接削减负荷的特点，行政部门、医疗机构等公共类用户的用能时间更加灵活，用能品质相对较低，具有更大的灵活性负荷削减潜力，所以RIES中可削减负荷适用于用户负荷需求中的公共建筑用电负荷和温控负荷。经过负荷削减后，用户在i时刻的p类负荷总需求量如式（17）所示：
$$ {U}_{\text{cut},i}^{p}=\text{ }{U}_{\text{o},i}^{p}-{\phi }_{\text{s},i}{U}_{\text{r},i}^{p} $$ (17) 式中：
$ U_{{\text{cut}},i}^p $、$ U_{r,i}^p $ ——用户i时刻n类可削减负荷和可削减的负荷需求量（kWh、kWh）；
$ {\varphi _{{\text{s}},i}} $ ——负荷削减率。$ p \in \{ {\text{e,\;h,\;c}}\} $，e代表建筑用电，h代表建筑用热、c代表建筑用冷。
-
经济补偿模型主要考虑了供能侧经济补偿对用户需求响应的引导作用。
对于可平移负荷，其单位负荷平移补偿$ {\mathrm{E}}{{\mathrm{C}}_{{\text{tran}},\;i}}$与平移的负荷总量有关：
$$ {C_{{\text{ec,\;tran}}}} = \sum (U_{{\text{tran}},\;i}^m {\mathrm{E}}{{\mathrm{C}}_{{\text{tran}},\;i}}) $$ (18) 式中：
${C_{{\text{ec,\;tran}}}}$ ——用户进行负荷平移需要的补偿（元/kWh）。
可调度负荷的单位负荷调度补偿与调度的时刻和负荷总量有关：
$$ {C_{{\text{ec,\;disp}}}} = \sum \left( {{\sigma _{{{a}},\;i}} L_{{\text{a}},\;i}^n {\mathrm{EC}}_{{\text{disp}},\;i}^{\text{a}} + {\sigma _{{{s}},\;i}} L_{{\text{s}},\;i}^n {\mathrm{EC}}_{{\text{disp}},\;i}^{\text{s}}} \right) $$ (19) 式中：
${C_{{\text{ec,\;disp}}}}$ ——用户参与需求响应的负荷调度补偿（元/kWh）；
${\mathrm{EC}}_{{\text{disp}},\;i}^{\text{a}}$、$ {\mathrm{EC}}_{{\text{disp}},\;i}^{\text{s}}$ ——i时刻用户接收负荷与转出负荷的单位负荷调度补偿（元/kWh）。
可削减负荷的单位负荷平移补偿$ {\mathrm{E}}{{\mathrm{C}}_{{{{\mathrm{cut}},}i}}}$与削减的负荷总量有关：
$$ {C_{{\text{ec,\;cut}}}} = \sum (U_{{\text{r,}\;i}}^n {\mathrm{E}}{{\mathrm{C}}_{{\text{cut,}\;i}}}) $$ (20) $$ E{C_{{\text{cut,}}\;i}} = {{a}} + {{b}} {\varphi _{{\text{s}},\;i}} + {{c}} \varphi _{s,\;i}^2 + {{d}} \varphi _{s,\;i}^3 $$ (21) 式中：
$ {C_{{\text{ec,\;cut}}}} $ ——用户进行负荷削减所需提供的补偿金额（元/kWh）；
$ {\mathrm{E}}{{\mathrm{C}}_{{\text{cut,}}\;\;i}} $ ——i时刻单位负荷削减补偿，该值与负荷削减率有关（元/kWh）；
a、b、c、d ——常数。
则：
$$ {C_{{\text{ec}}}} = {C_{{\text{ec,tran}}}} + {C_{{\text{ec,disp}}}} + {C_{{\text{ec,cut}}}} $$ (22) -
供能侧能量流动过程包括经历了能源生产、能源转换以及能源储放共3个环节。
能源生产过程中，以天然气为一次能源的能源生产设备数学模型如式（23）～（25）所示。
$$ {H_{{\text{GT}},i}} = {\alpha _{{\text{GT}}}} {E_{{\text{GT}},i}} $$ (23) $$ {E_{{\text{GT}},i}} = {x_{{\text{GT}},i}} {P_{{\text{GT}}}} \Delta {{T}} $$ (24) $$ {G_{{\text{ng}},i}} = {E_{{\text{GT}},{{i}}}}/({{{r}}_{{\text{ng}}}} {{{\eta}}_{{\text{GT}}}}) + {P_{{\text{GB}},i}} \Delta {{T}}/\left( {{{{r}}_{{\text{ng}}}} {{{\eta}}_{{\text{GB}}}}} \right) $$ (25) 式中：
${E_{{\text{GT}},i}}$、${H_{{\text{GT}},i}}$、${x_{{\text{GT}},i}}$ ——燃气轮机i时刻的发电量，产热量与运行负荷率（kWh、kWh、%）；
${P_{{\text{GT\;}}}}$ ——燃气轮机额定发电功率（kW）；
${\alpha _{{\text{GT\;}}}}$ ——燃气轮机的热电比；
${G_{{\text{ng}},i\;}}$ ——能源系统i时刻消耗的天然气量（m3）；
$ {{r}}_{\mathrm{n}\mathrm{g}} $ ——天然气的热值（kWh/m3）；
$ {\mathrm{\eta }}_{\mathrm{G}\mathrm{T}} $、$ {\mathrm{\eta }}_{\mathrm{G}\mathrm{B}} $ ——燃气轮机的电转换效率与燃气锅炉的热转换效率；
${P_{{\text{GB}},i}}$ ——燃气锅炉i时刻的产热功率（kW）。
以可再生能源为一次能源的能源生产设备数学模型如式（26）～（28）所示：
$$ {E_{{\mathrm{PV}},i}} = {H_{{\mathrm{A}},i}} {P_{{\text{AZ}}}} {{K}} \Delta {{T}}/{{{E}}_{\text{s}}} $$ (26) $$ {H_{{\text{PH}},i}} = {I_{{\text{t}},i}}{A_{\text{c}}}{{\eta}_{{\text{PH}}}}\left( {1 - {{\eta}_{\text{L}}}} \right)\Delta {{T}} $$ (27) $$ {E}_{{\mathrm{WT}},i}=\left\{ {\begin{array}{c}{P}_{\text{WT}} \dfrac{{v}_{i}-{{v}}^{{{\mathrm{in}}}}}{{{v}}^{0}-{v}^{{{\mathrm{in}}}}} \Delta T,{{v}}^{\text{in}}\leqslant {\nu }_{i} < {{v}}^{0}\\ {P}_{\text{WT}} \Delta T,{{v}}^{0}\leqslant {\nu }_{i}\end{array}} \right. $$ (28) 式中：
${E_{{\mathrm{PV}},i}}$、${H_{{\text{PH}},i}}$ ——光伏设备和太阳能集热器i时刻的发电量和产热量（kWh）；
${H_{{\mathrm{A}},i}}$ ——i时刻的水平面太阳能辐照量（kW/m2）；
${P_{{\text{AZ}\;\;}}}$ ——光伏设备安装容量（kW）；
${{{E}}_{\text{s}\;\;}}$ ——辐照度（kW/m2）；
$ {K}_{\;} $ ——光伏设备综合效率系数；
${I_{{\text{t}},i}}$ ——i时刻的太阳能辐照强度（kW/m2）；
${A_{\text{c}}}$ ——吸热板总面积（m2）；
$ {\mathrm{\eta }}_{\mathrm{P}\mathrm{H}\;} $ ——太阳能集热系统热效率；
${\eta _{\text{L}}}$ ——太阳能集热系统管道热损率；
${P_{{\text{WT}\;}}}$ ——风力发电机的额定发电功率（kW）；
${v_i}$ ——i时刻的实际风速（m/s）；
${{{\nu }}^{{\text{in}}}}$、${{\nu }^0}$ ——风力发电机的切入风速和额定风速（m/s、m/s）；
${E_{{\mathrm{WT}},i}}$ ——i时刻风力发电机的发电量(kWh)。
能源生产环节输出的电、热能流经能源转换及储放环节，得到终端能源的过程可用下列公式表示。其中，能源储存设备间各能流的转换关系如式（29）所示：
$$ \Delta {\mathrm{E}}{{\mathrm{S}}_{{\text{n}},i}} = \left( {P_{{\text{n}},i}^{{\text{cha}}} \theta _{\text{n}}^{{\text{cha}}} {{\eta}}_{\text{n}}^{{\text{cha}}} - P_{{\text{n}},i}^{{\text{dis}}} \theta _{\text{n}}^{{\text{dis}}} / {\eta}_{\text{n}}^{{\text{dis}}}} \right) \Delta {{T}} $$ (29) 式中：
$\Delta {\mathrm{E}}{{\mathrm{S}}_{{\text{n}},i}}$ ——某时间段内储能设备的净储能量，包括蓄电设备、蓄热设备、蓄冷设备（kWh）；
$P_{{\text{n}},i}^{{\text{cha}}}$、$P_{{\text{n}},i}^{{\text{dis}}}$ ——i时刻储能设备的蓄能功率和放能功率（kW）；
$\theta _{\text{n}}^{{\text{cha}}}$、$ {\mathrm{\theta }}_{\mathrm{n}}^{\mathrm{d}\mathrm{i}\mathrm{s}} $ ——i时刻储能设备的蓄能状态和放能状态，为0～1变量；
$ {\mathrm{\eta }}_{\mathrm{n}}^{\mathrm{c}\mathrm{h}\mathrm{a}} $、$ {\mathrm{\eta }}_{\mathrm{n}}^{\mathrm{d}\mathrm{i}\mathrm{s}} $ ——储能设备的蓄能效率和放能效率。
RIES输出至终端的能源如式（30）～（34）所示：
$$ U_i^{\text{e}} = {E_{{\text{GT}},i}} + {E_{{\text{PV}},i}} + {E_{{\text{WT}},i}} + {E_{{\text{grid}},i}} - {E_{{\text{sell}},i}} - {E_{{\text{EC}},i}} - {E_{{\text{EL}},i}} - \Delta {\mathrm{E}}{{\mathrm{S}}_{{\text{e}},i}} $$ (30) $$ U_i^{\text{c}} = {E_{{\text{EC}},i}}{{\delta}_{{\text{EC}},{\text{i}}}}{\text{CO}}{{\text{P}}_{{\text{EC}}}} + {H_{{\text{GT}},i}}{{\delta}_{{\text{AC}},i}}{{\eta}_{{\text{WHB}}}}{\text{CO}}{{\text{P}}_{{\text{AC}}}} - \Delta {\mathrm{E}}{{\mathrm{S}}_{{\text{c}},i}} $$ (31) $$ U_i^{{\text{pc}}} + U_i^{{\text{dc}}} = {E_{{\text{EC}},i}}\left( {1 - {{\beta}_{{\text{EC}},{{i}}}}} \right){\text{CO}}{{\text{P}}_{{\text{EC}}}} $$ (32) $$ U_i^{\text{h}} = {H_{{\text{EL}},i}} + {H_{{\text{PL}},i}} + {H_{{\text{GT}},i}}{{\delta}_{{\text{HX}},i}}{{\eta}_{{\text{WHB}}}}{{\eta}_{{\text{HX}}}} - \Delta {\mathrm{E}}{{\mathrm{S}}_{{\text{h}},i}} $$ (33) $$ U_i^{{\text{ph}}} + U_i^{{\text{dh}}} = {H_{{\text{GT}},i}}{{\eta}_{{\text{WHB}}}}{{\delta}_{{\text{tech}},i}} + {P_{{\text{GB}},i}}\Delta {{T}} $$ (34) 式中：
$U_i^{\text{e}}$、$U_i^{\text{c}}$、$U_i^{{\text{pc}}}$、$U_i^{{\text{dc}}}$、$U_i^{\text{h}}$、$U_i^{{\text{ph}}}$、$U_i^{{\text{dh}}}$ ——i时刻RIES的电、建筑用冷、过程工业用冷、离散制造用冷、生活热水、过程工业用热、离散制造用热终端能源输出量（kWh）；
${E_{{\text{grid}},i}}$ ——i时刻RIES的网电购买量(kWh)；
${E_{{\text{EC}},i}}$、${E_{{\text{EL}},i}}$——i时刻电制冷机组和电热锅炉消耗的电量(kWh)；
$ {{\delta }}_{\mathrm{E}\mathrm{C},{i}} $ ——i时刻电制冷机组产生的终端建筑用冷负荷量占电制冷机组总产冷量的比例；
$ {{\delta }}_{\mathrm{A}\mathrm{C},{i}} $、$ {{\delta }}_{\mathrm{H}\mathrm{X},{i}} $、$ {{\delta }}_{\mathrm{t}\mathrm{e}\mathrm{c}\mathrm{h},{i}} $——i时刻余热锅炉输至吸收式制冷机组，换热器及终端工艺用户的热量占余热锅炉总产热量的比例；
$ {\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{E}\mathrm{C}} $、$ {\mathrm{C}\mathrm{O}\mathrm{P}}_{\mathrm{A}\mathrm{C}} $ ——电制冷机组与吸收式制冷机组的制冷性能系数；
${H_{{\text{EL}},i}}$ ——i时刻电热锅炉的产热量（kW）；
$ {{\eta }}_{\mathrm{W}\mathrm{H}\mathrm{B}} $、$ {{\eta }}_{\mathrm{H}\mathrm{X}} $——余热锅炉与换热器的效率。
-
该RIES优化模型还应包括以下约束：
1) 储能设备运行状态约束，如式（35）～（37）所示。
$$ 0 \leqslant P_{p,i}^{{\text{cha}}} \leqslant {{x}}_{p,{\text{cha}}}^{{\text{max}}} {\mathrm{E}}{{\mathrm{S}}_p} $$ (35) $$ 0 \leqslant P_{p,i}^{{\text{dis}}} \leqslant {{x}}_{p,{\text{dis}}}^{{\text{max}}} {\mathrm{E}}{{\mathrm{S}}_p} $$ (36) $$ \theta _{{{p}},i}^{{\text{cha}}} \theta _{n,i}^{{\text{dis}}} = 0 $$ (37) 式中：
${{x}}_{n,{\text{cha}}}^{{\text{max}}}$ ——储能功率的上限系数；
${{x}}_{n,{\text{dis}\;}}^{{\text{max}}}$ ——放能功率的上限系数。
2) RIES各能流匹配约束：
电负荷平衡约束
$$ U_i^{\text{e}} \geqslant U_{{\text{tran}},i}^{\text{e}} + U_{{\text{disp}},i}^{\text{e}} + U_{{\text{cut}},i}^{\text{e}} $$ (38) 冷负荷平衡约束
$$ U_i^{{\text{pc}}} \geqslant U_{{\text{tran}},i}^{{\text{pc}}} $$ (39) $$ U_i^{{\text{dc}}} \geqslant U_{{\text{disp}},i}^{{\text{dc}}} $$ (40) $$ U_i^{\text{c}} \geqslant U_{{\text{cut}},i}^{\text{c}} $$ (41) 热负荷平衡约束
$$ U_i^{{\text{ph}}} \geqslant U_{{\text{tran}},i}^{{\text{ph}}} $$ (42) $$ U_i^{{\text{dh}}} \geqslant U_{{\text{disp}},i}^{{\text{dh}}} $$ (43) $$ U_i^{\text{h}} \geqslant U_{{\text{cut}},i}^{\text{h}} $$ (44) -
该模型属于混合整数非线性规划模型，使用传统的遗传算法求解则收敛速度慢、收敛精度差。在MATLAB环境下选用的混合差分遗传算法[24]采用实数编码产生初始种群，避免了传统遗传算法采用二进制编码过于复杂的缺点。同时，在求解过程中通过差分算法中的交叉、变异、选择等操作，可以增加种群多样性，具有搜索空间大、求解速度快、收敛精度高等特点。模型求解首先在用户侧需求响应模型中，可获得满足需求响应约束条件下需求响应方案及用户侧逐时负荷，并作为供能侧能量流动模型的输入。然后基于目标函数和约束条件对模型进行求解寻优，直到目标函数实现最优时可得到RIES的用户侧需求响应策略、各设备最佳装机容量以及运行策略。
-
选取位于中国南方某一需求响应潜力丰富的综合性工业园区为研究案例，该园区包括工业企业、公共建筑、商业建筑等多种用户类型，终端用能覆盖面较广且用能需求多样。从园区全年中选取1个典型日来研究园区内终端用户冷热电负荷的用能特征，如图2所示。
图 2 工业园区典型日终端负荷需求
Figure 2. Terminal load demand of industrial park in typical day
从图2可以看出，园区16:00峰值用电需求达到18.63 MW，典型日用电负荷峰谷比为3.13。同时，典型日内园区冷负荷和电负荷的波动规律相似，冷负荷在15:00需求达到15.64 MW，峰谷差为12.76 MW。而热负荷存在较长时间的用能高峰，12:00－18:00负荷均在20 MW以上，峰谷差为14.47 MW。
-
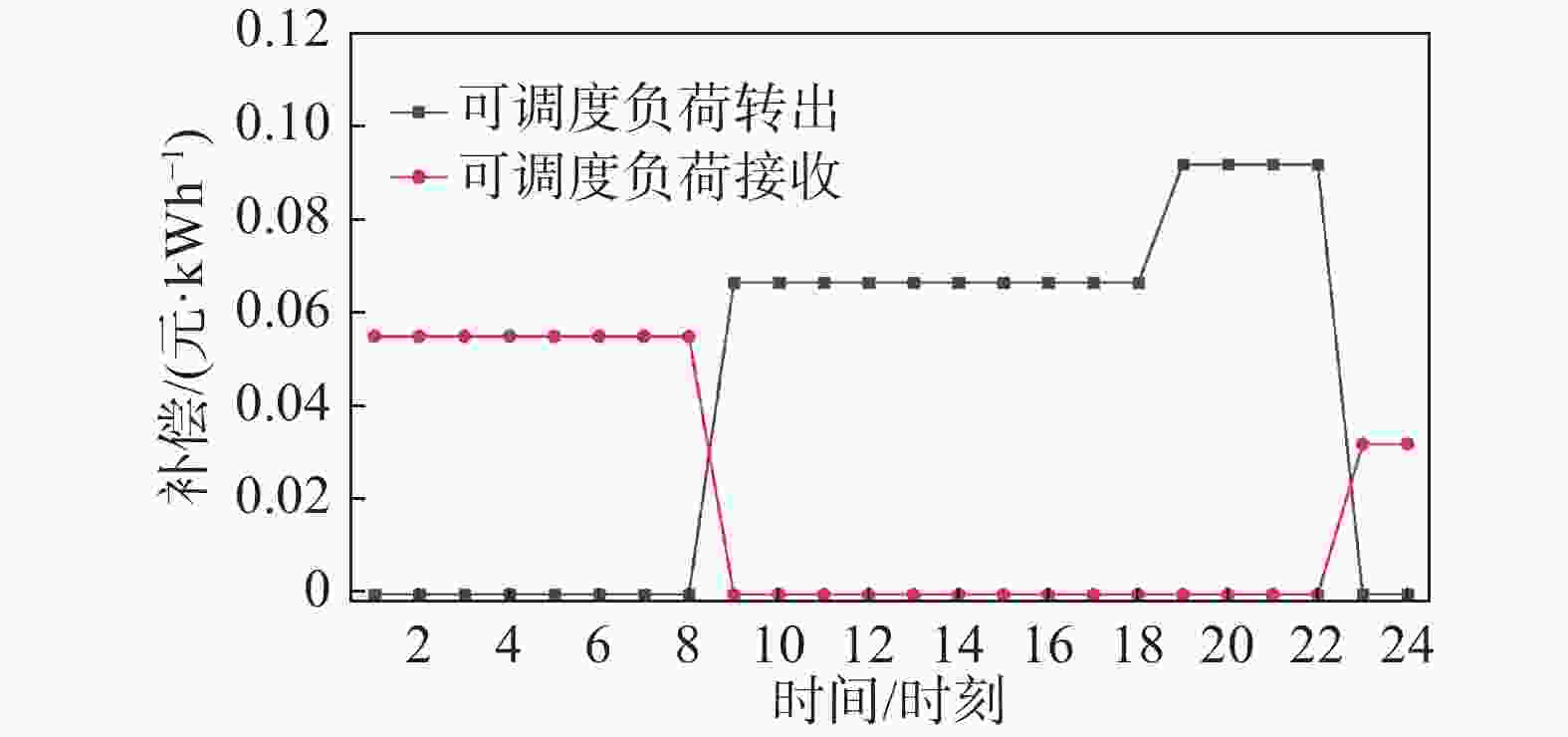
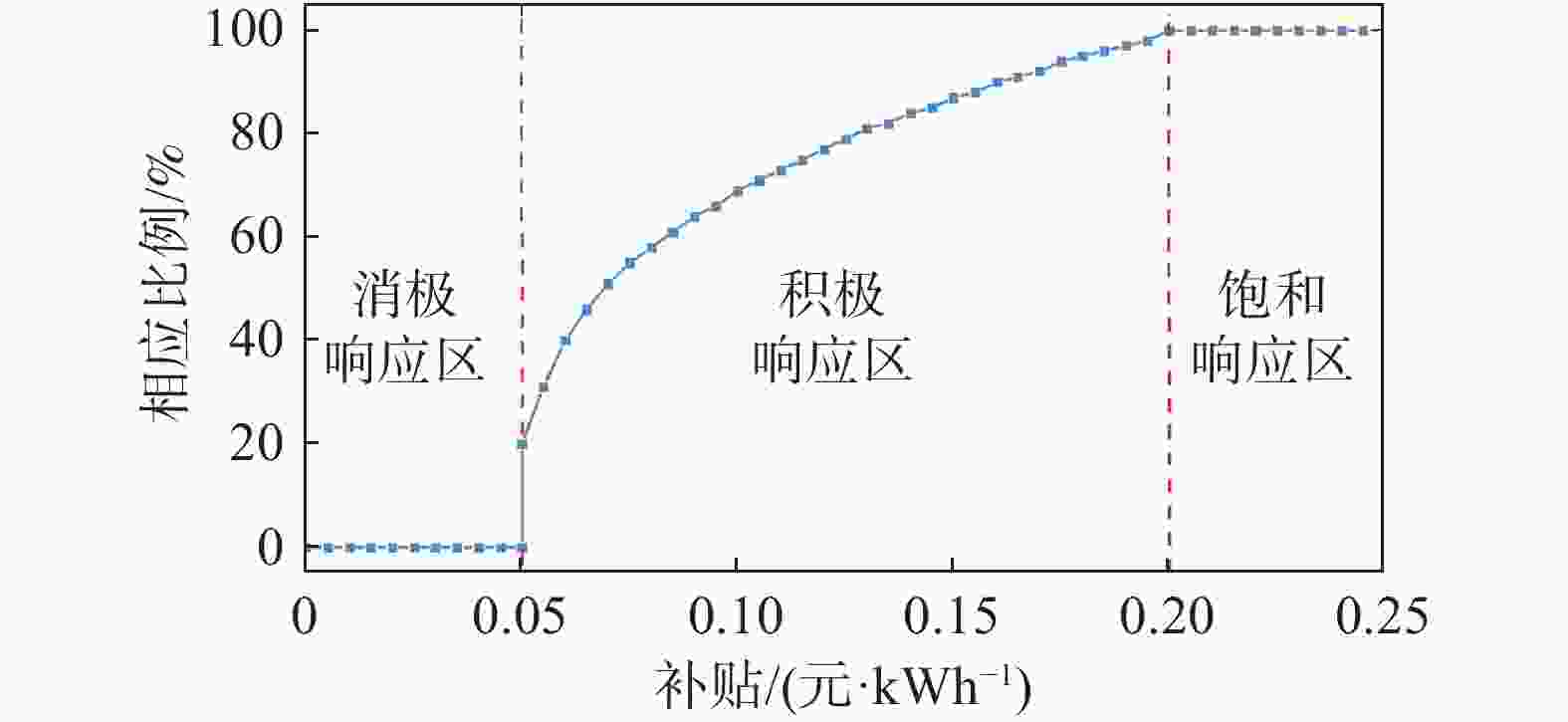
本案例参考分时电价机制制定可平移负荷的经济补偿方案，该园区过程工业单位负荷补偿金额如表1所示。该园区中离散制造业生产用能负荷可以调度，不同时段的接收和转出补偿价格如图3所示。在实际需求响应实施过程中，由于人们对室内建筑供冷和生活热水温度变化敏感程度高，不易改变用户生活习惯，所以只对公共类建筑用电削减进行讨论，如图4所示。在构建的综合评价体系的基础上利用层次分析法[25]，邀请行业领域专家、技术人员和用户代表使用数字1～9作为评分区间，对目标函数中各评价指标两两之间的重要性进行评分和排序，并建立判断矩阵。当判断矩阵的一致性检验结果小于0.1时，判断矩阵的特征值即为各个评价指标的权重因子。同时综合衡量用户参与需求响应的积极性，通过层次分析法确定案例中各个评价指标的权重因子分别为0.5，0.3，0.1，0.1。
表 1 可平移负荷的经济补偿机制
Table 1. The economic compensation mechanism of shiftable load
时段 工艺用电/
（元·kwh−1）工艺冷/
（元·kwh−1）工艺蒸汽/
（元·kwh−1）谷段 0:00～8:00 0.070 0.018 0.020 高峰 8:00～12:00 0.038 0.015 0.015 平段 12:00～18:00 0.050 0.016 0.018 22:00～24:00 0.050 0.016 0.018 尖段 18:00～22:00 0.000 0.000 0.000 
图 3 可调度负荷的经济补偿机制
Figure 3. Economic compensation mechanism of dispatchable load
图 4 可削减电负荷的经济补偿机制
Figure 4. Economic compensation mechanism of reducible load
-
根据所建立的模型和能源设备相关参数[21]，采用混合差分遗传算法求得RIES负荷需求响应策略如图5（a）所示。工业用户某段工艺流程的电负荷比需求响应实施前平移了12 h，由12:00-18:00平移至24:00-次日6:00，负荷的使用顺序和数量均没有发生改变。公共建筑用户14:00-18:00的可调度电负荷数量集中起来，转移至7:00。工艺冷负荷和工艺热负荷与电负荷拥有相同的需求响应调度时序，如图5（b），图5（c）所示。通过需求响应前后的对比可以看出，在需求响应的过程中可平移负荷和可调度负荷实现了用能曲线的削峰填谷，可削减负荷直接降低了高峰期内的用电负荷，使得各时段的用能负荷尽可能趋于一致。
图 5 RIES负荷需求响应策略
Figure 5. RIES demand response strategy
-
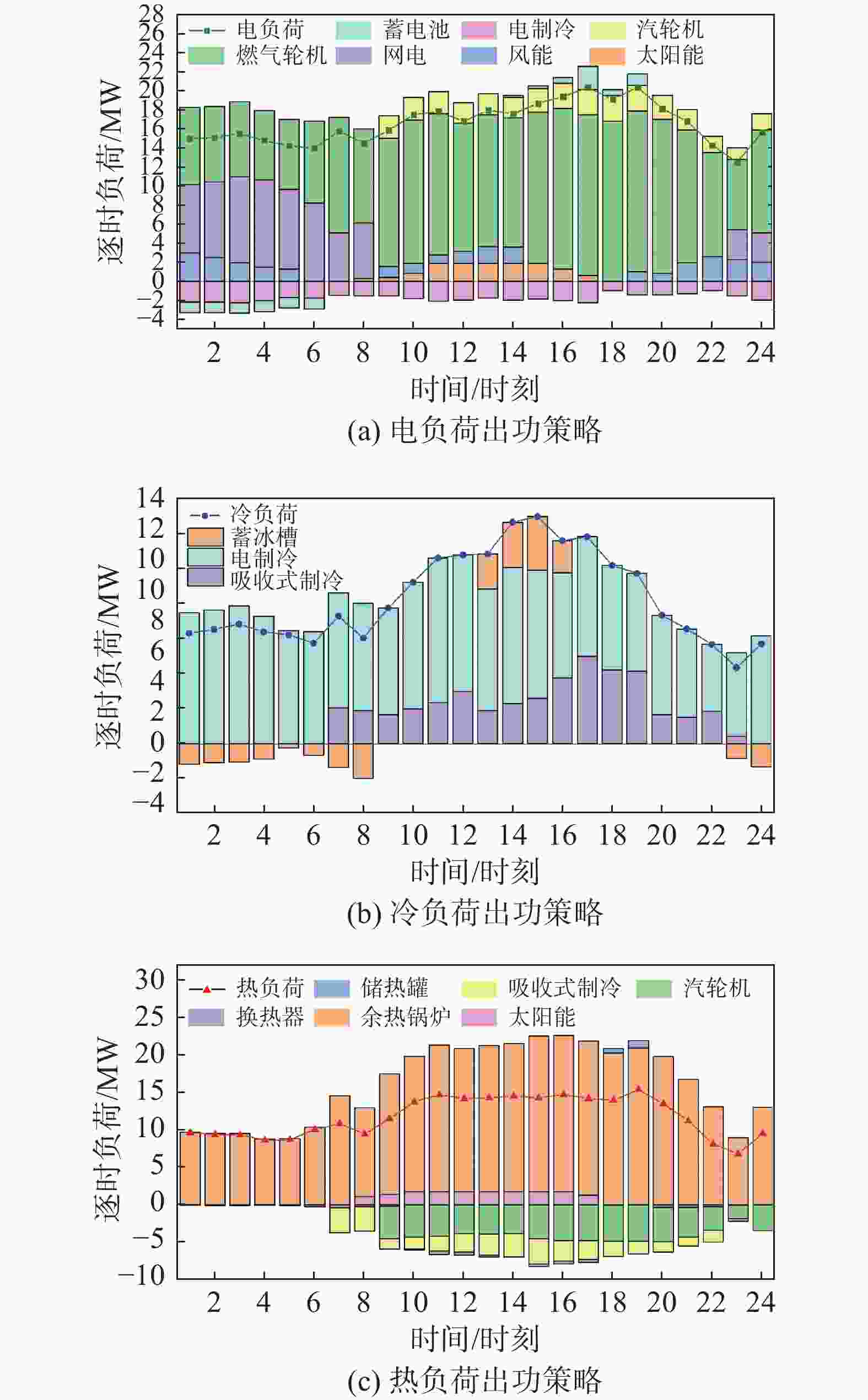
考虑冷热电负荷需求响应的RIES的安装方案和最优逐时运行策略分别如表2和图6所示。
表 2 各技术设备装机方案
Table 2. Installation scheme of various technical equipment
技术设备 额定容量/MW 燃气轮机 11.40 风力发电机 2.64 光伏电池 2.13 太阳能集热器 1.71 汽轮机 3.38 电制冷 8.16 余热锅炉 22.13 吸收式制冷 3.38 蓄电池 1.85 储热罐 0.73 蓄冷箱 3.73 
图 6 工业园区逐时运行策略
Figure 6. Hourly operation strategy of industrial park
从图6中可以看出，需求响应后用电、用冷负荷分布较为均衡，1:00-8:00和21:00-24:00电力负荷需求由燃气轮机、风电和网电共同满足。同时，由于夜间电价较低，电蓄冰装置通过购买便宜的网电制冰并储存起来从而转移能源压力，这一时期的冷负荷需求全部由电制冷机组提供。9:00-22:00，用电和冷负荷需求处于较高时段并存在用能高峰期，这一时期用电需求通过燃气轮机、风力发电和太阳能发电满足，用冷负荷需求主要由电制冷和吸收式冷水机组提供，用冷高峰期不足的冷负荷由夜间储存的冷负荷来满足。但是，用户侧的用热负荷曲线不同于典型日的用电负荷和用冷负荷，因此设备的能量输出特性也不同。1:00-7:00和23:00-24:00，余热锅炉在耗热低谷期间提供热量。在用户热负荷高峰期8:00-17:00，系统负荷由太阳能集热器、余热锅炉和换热器满足，同时有部分蒸汽进行吸收式制冷，多余的热量储存在储热罐中。17:00-21:00，用户热负荷逐渐降低，系统部分热负荷由白天蓄热箱储存的热量补充。通过分析典型日的供需形势，考虑冷热电负荷需求响应的RIES兼顾经济性、负荷峰谷差和碳排放，尽可能利用廉价的电网电力和清洁的可再生能源，合理运行储能设备，有效缓解了冷热电负荷供需匹配的矛盾。
-
表3显示了冷热电负荷需求响应前后RIES的各评价指标对比。需求响应后的电负荷峰谷差减小29.7%，极大地提高了供电稳定性。在经济性方面，需求响应分别节约能源供给侧投资成本和用户侧购能成本405万元、638万元，同时能源系统可减少碳排放1 345 t。实施需求响应在减小负荷峰谷差、降低碳排放的基础上，保证了RIES供需双方的经济效益。
表 3 需求响应前后RIES各评价指标的对比
Table 3. Comparison of RIES evaluation indexes before and after demand response
评价指标 总成本/
万元碳排放量/t 电负荷峰谷比 用户侧购能
成本/万元需求响应前 10 938 60 762 3.13 12 572 需求响应后 10 533 59 417 2.20 11 934 -
文章依据能量流动关系与供需平衡约束，建立了以年总成本、电负荷峰谷比、用户购能成本和碳排放量等评价指标最优为目标函数的考虑冷热电负荷需求响应的区域综合能源系统优化模型。该优化模型包括需求响应模块和能量流动模块，并将冷热电灵活性负荷资源按照负荷类型和用能特点分为可平移负荷、可调度负荷和可削减负荷，对应不同的需求响应策略。
通过选取某工业园进行案例分析，与未考虑需求响应的能源系统相比，实施冷热电负荷需求响应的RIES总成本降低了3.70%，电负荷峰谷比降低了29.7%，用户购能成本节省5.07%，碳排放量减少了2.21%，验证了所建模型的可行性和实用性。
模型结果表明通过可平移、可调度负荷的削峰填谷以及可削减负荷的辅助削峰，RIES实施需求响应使得用户用能曲线变得均衡平缓，有利于提高供需双方的经济效益，协同优化RIES装机规模和运行策略。
Optimization of Regional Integrated Energy System Operation Considering Flexible Load Demand Response for Cooling, Heating and Power
-
摘要:
目的 随着能源领域改革的不断深入，引入市场因素引导下的需求响应机制已经成为区域综合能源系统（RIES）发展的必然趋势。 方法 基于RIES中多种能流的耦合特性，同时根据用户的用能特点和需求响应潜力，将参与多种灵活性负荷资源划分为可平移负荷、可调度负荷以及可削减负荷，建立了考虑冷热电灵活性负荷需求响应的RIES运行优化模型。模型以供需双方的经济效益、电负荷峰谷比以及碳排放量等综合评价指标为优化目标，求解得到负荷需求响应方案和各能源网络的优化结果。 结果 算例结果表明，需求响应使RIES的总成本降低了3.70%，电负荷峰谷比降低了29.7%。 结论 验证了文章所建模型的可行性和实用性。 Abstract:Introduction As the reform in the energy sector continues to deepen, the introduction of a demand response mechanisms guided by market factors have become an inevitable trend in the development of regional integrated energy system (RIES). Method Based on the coupling characteristics of multiple energy flows in RIES, three different flexible loads were divided according to the demand response potential and user energy consumption characteristics, which were shiftable load, dispatchable load and reducible load. Finally, a RIES operation optimization model was established considering the flexible load demand response for cooling, heating and power. The load demand response plan and the optimization results of each energy network are obtained by using the economic benefits of both supply and demand sides, the peak and valley values of electricity load, and the values of carbon emissions as the optimization objective of the model. Result The results indicate that demand response reduces the total cost of RIES by 3.70% and the peak to valley ratio of electricity load by 29.7%. Conclusion The feasibility and practicality of the proposed model are verified in this paper. -
Key words:
- regional integrated energy system /
- demand response /
- peak load shifting /
- operation strategy /
- load
-
表 1 可平移负荷的经济补偿机制
Tab. 1. The economic compensation mechanism of shiftable load
时段 工艺用电/
（元·kwh−1）工艺冷/
（元·kwh−1）工艺蒸汽/
（元·kwh−1）谷段 0:00～8:00 0.070 0.018 0.020 高峰 8:00～12:00 0.038 0.015 0.015 平段 12:00～18:00 0.050 0.016 0.018 22:00～24:00 0.050 0.016 0.018 尖段 18:00～22:00 0.000 0.000 0.000 
下载: 导出CSV
表 2 各技术设备装机方案
Tab. 2. Installation scheme of various technical equipment
技术设备 额定容量/MW 燃气轮机 11.40 风力发电机 2.64 光伏电池 2.13 太阳能集热器 1.71 汽轮机 3.38 电制冷 8.16 余热锅炉 22.13 吸收式制冷 3.38 蓄电池 1.85 储热罐 0.73 蓄冷箱 3.73
下载: 导出CSV
表 3 需求响应前后RIES各评价指标的对比
Tab. 3. Comparison of RIES evaluation indexes before and after demand response
评价指标 总成本/
万元碳排放量/t 电负荷峰谷比 用户侧购能
成本/万元需求响应前 10 938 60 762 3.13 12 572 需求响应后 10 533 59 417 2.20 11 934
下载: 导出CSV
-
[1] 张沈习, 王丹阳, 程浩忠, 等. 双碳目标下低碳综合能源系统规划关键技术及挑战 [J]. 电力系统自动化, 2022, 46(8): 189-207. DOI: 10.7500/AEPS20210703002. ZHANG S X, WANG D Y, CHENG H Z, et al. Key technologies and challenges of low-carbon integrated energy system planning for carbon emission peak and carbon neutrality [J]. Automation of electric power systems, 2022, 46(8): 189-207. DOI: 10.7500/AEPS20210703002. [2] 蔡绍宽. 双碳目标的挑战与电力结构调整趋势展望 [J]. 南方能源建设, 2021, 8(3): 8-17. DOI: 10.16516/j.gedi.issn2095-8676.2021.03.002. CAI S K. Challenges and prospects for the trends of power structure adjustment under the goal of carbon peak and neutrality [J]. Southern energy construction, 2021, 8(3): 8-17. DOI: 10.16516/j.gedi.issn2095-8676.2021.03.002. [3] 贠保记, 张恩硕, 张 国, 等. 考虑综合需求响应与“双碳”机制的综合能源系统优化运行 [J]. 电力系统保护与控制, 2022, 50(22): 11-19. DOI: 10.19783/j.cnki.pspc.220621. YUN B J, ZHANG E S, ZHANG G, et al. Optimal operation of an integrated energy system considering integrated demand response and a "dual carbon" mechanism [J]. Power system protection and control, 2022, 50(22): 11-19. DOI: 10.19783/j.cnki.pspc.220621. [4] 胡程平, 范明, 刘艾旺, 等. 考虑云储能的多区互联综合能源系统规划 [J]. 发电技术, 2024, 45(4): 641-650. DOI: 10.12096/j.2096-4528.pgt.23057. HU C P, FAN M, LIU A X, et al. Multi-area interconnected integrated energy system planning considering cloud energy storage [J]. Power generation technology, 2024, 45(4): 641-650. DOI: 10.12096/j.2096-4528.pgt.23057. [5] 李鹏, 吴迪凡, 李雨薇, 等. 基于综合需求响应和主从博弈的多微网综合能源系统优化调度策略 [J]. 中国电机工程学报, 2021, 41(4): 1307-1321. DOI: 10.13334/j.0258-8013.pcsee.201845. LI P, WU D F, LI Y W, et al. Optimal dispatch of multi-microgrids integrated energy system based on integrated demand response and stackelberg game [J]. Proceedings of the CSEE, 2021, 41(4): 1307-1321. DOI: 10.13334/j.0258-8013.pcsee.201845. [6] 罗志斌, 孙潇, 孙翔, 等. 氢能与储能耦合发展的机遇与挑战 [J]. 南方能源建设, 2022, 9(4): 24-31. DOI: 10.16516/j.gedi.issn2095-8676.2022.04.003. LUO Z B, SUN X, SUN X, et al. The coupling development of hydrogen and energy storage technology: opportunities and challenges [J]. Southern energy construction, 2022, 9(4): 24-31. DOI: 10.16516/j.gedi.issn2095-8676.2022.04.003. [7] 亢猛, 钟祎勍, 石鑫, 等. 计及负荷供给可靠性的园区综合能源系统两阶段优化方法研究 [J]. 发电技术, 2023, 44(1): 25-35. DOI: 10.12096/j.2096-4528.pgt.21110. KANG M, ZHONG Y Q, SHI X, et al. Research on two-stage optimization approach of community integrated energy system considering load supply reliability [J]. Power generation technology, 2023, 44(1): 25-35. DOI: 10.12096/j.2096-4528.pgt.21110. [8] 董帅, 王杉, 李昊, 等. 考虑网络特性的综合能源系统多时间尺度调度方法 [J]. 山东电力技术, 2023, 50(6): 20-26. DOI: 10.20097/j.cnki.issn1007-9904.2023.06.004. DONG S, WANG S, LI H, et al. Multi-time scale scheduling method for integrated energy system considering network characteristics [J]. Shandong electric power, 2023, 50(6): 20-26. DOI: 10.20097/j.cnki.issn1007-9904.2023.06.004. [9] 孟明, 商聪, 马思源, 等. 基于区块链的综合能源系统低碳优化调度研究 [J]. 华北电力大学学报, 2023, 50(3): 67-80. DOI: 10.3969/j.ISSN.1007-2691.2023.03.07. MENG M, SHANG C, MA S Y, et al. Research on low-carbon scheduling of integrated energy system based on blockchain technology [J]. Journal of North China Electric Power University, 2023, 50(3): 67-80. DOI: 10.3969/j.ISSN.1007-2691.2023.03.07. [10] 侯慧, 戈翔迪, 吴细秀, 等. 运行与规划协同的电热氢联供系统最优容量配置研究 [J]. 电力系统保护与控制, 2022, 50(24): 144-151. DOI: 10.19783/j.cnki.pspc.220314. HOU H, GE X D, WU X X, et al. Optimal capacity allocation of an electricity heat hydrogen cogeneration system based on coordinated operation and planning [J]. Power system protection and control, 2022, 50(24): 144-151. DOI: 10.19783/j.cnki.pspc.220314. [11] 董亮, 黄励, 刘万根, 等. 电—热综合能源系统多目标优化 [J]. 电气自动化, 2023, 45(4): 54-56. DOI: 10.3969/j.issn.1000-3886.2023.04.017. DONG L, HANG L, LIU W G, et al. Multi-objective optimization of electric-thermal integrated energy system [J]. Electrical automation, 2023, 45(4): 54-56. DOI: 10.3969/j.issn.1000-3886.2023.04.017. [12] XIANG Y, CAI H H, GU C H, et al. Cost-benefit analysis of integrated energy system planning considering demand response [J]. Energy, 2020, 192: 116632. DOI: 10.1016/j.energy.2019.116632. [13] HE L C, LU Z G, GENG L J, et al. Environmental economic dispatch of integrated regional energy system considering integrated demand response [J]. International journal of electrical power & energy systems, 2020, 116: 105525. DOI: 10.1016/j.ijepes.2019.105525. [14] JIANG P, DONG J, HUANG H. Optimal integrated demand response scheduling in regional integrated energy system with concentrating solar power [J]. Applied thermal engineering, 2020, 166: 114754. DOI: 10.1016/j.applthermaleng.2019.114754. [15] 吴佩隆, 王维庆, 樊小朝, 等. 考虑氢负荷与综合需求响应的天然气制氢的园区综合能源系统优化配置 [J]. 现代电子技术, 2023, 46(7): 135-142. DOI: 10.16652/j.issn.1004-373x.2023.07.025. WU P L, WANG W Q, FAN X C, et al. Optimal configuration of industrial PIES for natural gas hydrogen production considering hydrogen load and comprehensive demand response [J]. Modern electronics technique, 2023, 46(7): 135-142. DOI: 10.16652/j.issn.1004-373x.2023.07.025. [16] 赵扉, 胡程平, 施云辉. 考虑温控负荷需求响应的电热联合系统多阶段鲁棒调度方法 [J]. 电力需求侧管理, 2022, 24(5): 15-21. DOI: 10.3969/j.issn.1009-1831.2022.05.004. ZHAO F, HU C P, SHI Y H. Multi-stage robust dispatch of integrated electric and heating system considering demand response of thermostatically controlled load [J]. Power demand side management, 2022, 24(5): 15-21. DOI: 10.3969/j.issn.1009-1831.2022.05.004. [17] 李东东, 王啸林, 沈运帷, 等. 考虑多重不确定性的含需求响应及电碳交易的虚拟电厂优化调度策略 [J]. 电力自动化设备, 2023, 43(5): 210-217, 251. DOI: 10.16081/j.epae.202303024. LI D D, WANG X L, SHEN Y W, et al. Optimal scheduling strategy of virtual power plant with demand response and electricity-carbon trading considering multiple uncertainties [J]. Electric power automation equipment, 2023, 43(5): 210-217, 251. DOI: 10.16081/j.epae.202303024. [18] 王凌云, 徐健哲, 李世春, 等. 考虑电-气-热需求响应和阶梯式碳交易的综合能源系统低碳经济调度 [J]. 智慧电力, 2022, 50(9): 45-52. DOI: 10.3969/j.issn.1673-7598.2022.09.008. WANG L Y, XU J Z, LI S C, et al. Low carbon economic dispatch of integrated energy system considering electricity-gas-heat demand response and tiered carbon trading [J]. Smart power, 2022, 50(9): 45-52. DOI: 10.3969/j.issn.1673-7598.2022.09.008. [19] 刘至纯, 李华强, 王俊翔, 等. 基于多时间尺度综合需求响应策略的综合能源系统优化运行 [J]. 电力建设, 2022, 43(9): 54-65. DOI: 10.12204/j.issn.1000-7229.2022.09.006. LIU Z C, LI H Q, WANG J X, et al. Optimal operation of integrated energy system based on multi-time scale integrated demand response strategy [J]. Electric power construction, 2022, 43(9): 54-65. DOI: 10.12204/j.issn.1000-7229.2022.09.006. [20] 吕智林, 易佳奇, 刘泉, 等. 含氢能利用和需求响应的综合能源系统低碳优化 [J]. 电力系统及其自动化学报, 2023, 35(7): 10-19. DOI: 10.19635/j.cnki.csu-epsa.001116. LÜ Z L, YI J Q, LIU Q, et al. Low-carbon optimization of integrated energy system with hydrogen energy utilization and demand response [J]. Proceedings of the CSU-EPSA, 2023, 35(7): 10-19. DOI: 10.19635/j.cnki.csu-epsa.001116. [21] 曹彬, 吕干云, 王楠, 等. 综合能源系统优化调度下的需求响应研究与应用 [J]. 电力需求侧管理, 2021, 23(4): 45-50. DOI: 10.3969/j.issn.1009-1831.2021.04.009. CAO B, LÜ G Y, WANG N, et al. Research and application of demand response based on optimal scheduling of integrated energy system [J]. Power demand side management, 2021, 23(4): 45-50. DOI: 10.3969/j.issn.1009-1831.2021.04.009. [22] 熊文, 刘育权, 苏万煌, 等. 考虑多能互补的区域综合能源系统多种储能优化配置 [J]. 电力自动化设备, 2019, 39(1): 118-126. DOI: 10.16081/j.issn.1006-6047.2019.01.018. XIONG W, LIU Y Q, SU W H, et al. Optimal configuration of multi-energy storage in regional integrated energy system considering multi-energy complementation [J]. Electric power automation equipment, 2019, 39(1): 118-126. DOI: 10.16081/j.issn.1006-6047.2019.01.018. [23] 杨海柱, 李梦龙, 江昭阳, 等. 考虑需求侧电热气负荷响应的区域综合能源系统优化运行 [J]. 电力系统保护与控制, 2020, 48(10): 30-37. DOI: 10.19783/j.cnki.pspc.190774. YANG H Z, LI M L, JIANG Z Y, et al. Optimal operation of regional integrated energy system considering demand side electricity heat and natural-gas loads response [J]. Power system protection and control, 2020, 48(10): 30-37. DOI: 10.19783/j.cnki.pspc.190774. [24] 李自成, 张赛, 王后能, 等. 基于混合差分遗传算法的Bouc-Wen迟滞模型辨识策略 [J]. 控制与决策, 2021, 36(2): 371-378. DOI: 10.13195/j.kzyjc.2019.0663. LI Z C, ZHANG S, WANG H N, et al. Bouc-Wen hysteresis model identification strategy based on hybrid differential genetic algorithm [J]. Control and decision, 2021, 36(2): 371-378. DOI: 10.13195/j.kzyjc.2019.0663. [25] 王海宁, 王正莹, 慕子煜, 等. 基于层次分析法的EPC总承包物资采购评标权重选取 [J]. 电力勘测设计, 2022(6): 1-5. DOI: 10.13500/j.dlkcsj.issn1671-9913.2022.06.001. WANG H N, WANG Z Y, MU Z Y, et al. Selection of evaluation weight of EPC material procurement based on AHP [J]. Electric power survey & design, 2022(6): 1-5. DOI: 10.13500/j.dlkcsj.issn1671-9913.2022.06.001. -
图(6) / 表 (3)
计量
- 文章访问数: 197
- HTML全文浏览量: 106
- PDF下载量: 12
- 被引次数: 0
