环境问题和化石燃料储量的减少使得当今能源系统正向可持续发展方向转变^[1]，近年来，基于可再生能源的各种发电技术得到了飞速发展。其中，风力发电技术作为一种可再生能源，因其诸多优势得到了广泛的研究和应用^[2]。特别是在沿海经济发达地区，聚集了大量电力负荷，但该类区域通常缺乏煤炭资源，土地资源宝贵，且人口密集，对环境要求较高，因此，开发海上风力发电已成为这些地区一种高效的新能源发电方法。然而，由于电网吸收能力弱、距主要陆地距离远、海上风资源和环境条件复杂等诸多不利因素，海上风力发电系统的运行和维护面临着严峻挑战。

针对这一问题，国内外学者提出了许多方法来解决海上风电场的稳定、安全、可靠和经济运行等问题。杨康等^[3]提出了一种基于风功率预测器的海上风机恒定功率控制方法，该方法充分考虑了荷电状态、充放电速率以及使用寿命等运行约束，以抑制风力发电的强波动性；张小莲^[4]提出了一种基于荷电状态和可变滤波器时间常数的改进海上风机恒定功率控制方法；吴晓刚^[5]研究了考虑高风电穿透率和爬坡率约束的运行可靠性和能效评估方法；张浩博^[6]提出了一种基于多智能体系统的分布式储能系统优化调度方法，该方法旨在实现发电和负荷平衡，以最大化其成本和能源效率等多个目标；张磊和于会群^[7-8]研究了风不确定性下的海上风电场经济调度模型。已有研究成果表明，大部分都未从受端电网运行稳定的角度，考虑海上风电与电池储能系统的协调控制机理，特别是在台风期间是海上风电场一方提升自身收益，但又需考虑突然脱网对受端电压电压频率的不稳定影响，因此，构建合理有效的海上风电与储能系统协调控制方法是未来海上风电场友好接入的关键因素。

为了实现台风期间海上风电友好接入，考虑到氢储能具有储存效率高、排放低和应用广泛等优点，本文提出了一种海上风电场与氢气管理系统之间的协同控制方法。台风临近时期，电池储能系统可在正常运行下最大限度地利用风能发电，并在台风过境期间作为海上风电的备用电源，以减小其对受端电网的不利影响，有效平移海上风电输出的波动性。本文首先详细介绍了海上风电场与氢能系统的物理建模方法及控制模型，并根据台风期间说明了二者之间的协同控制策略。最后，通过仿真验证了所提方法使海上风电场能够更灵活且友好地满足台风期间的并网运行。此外，氢储能系统可在正常运行下最大限度地利用风能发电，并在台风期间作为海上风电的备用电源，以减小其对受端电网的不利影响。

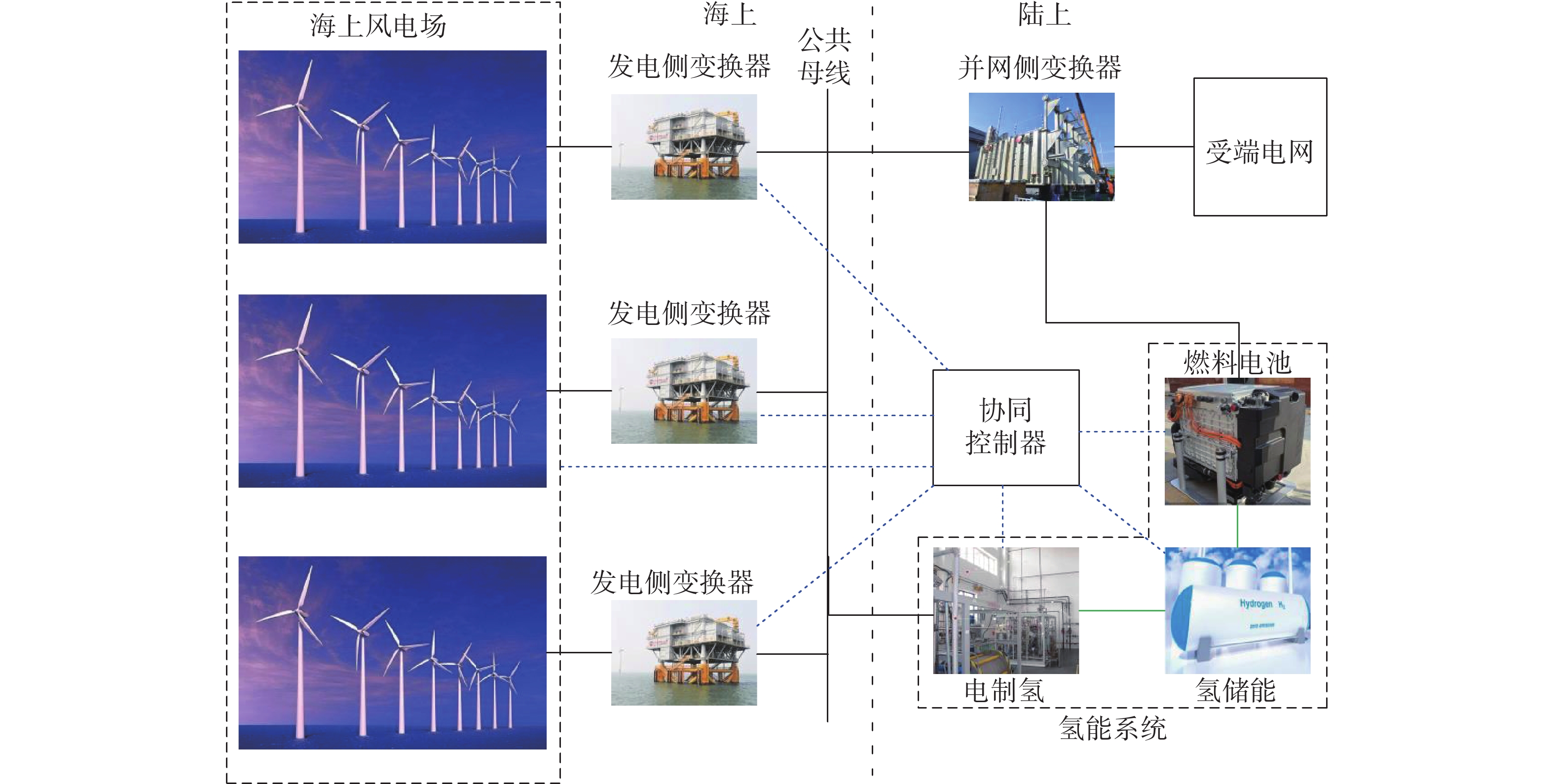
如图1所示，本文研究对象主要由海上风电场、氢能系统（其包括电制氢、氢储能和燃料电池（Fuel Cell，FC）等设备）、发电侧和并网侧变换器和本地负载组成。本地负载主要为负责风力发电机的监控系统（L_c）、偏航系统（L_y）、变桨系统（L_p）和其他负载（L_o）。图中黑色实线表示电能传输路径，绿色实线表示氢能传输路径，蓝色虚线表示信息传输和控制信号。考虑到安装氢能系统的可行性和水的可用性，氢能系统安装在近海陆上。氢能系统的电气接口连接到风电场输出的公共母线。当风电场输出的功率超过电网所需的功率时，氢能系统内的电制氢激活以吸收多余的电能并产生氢气。另一方面，如果电网需求超过风力发电场的输出功率，燃料电池将提供额外的电能。

图  1  含氢能系统的海上风电场机构示意图

Figure 1.  Schematic diagram of offshore wind farm with hydrogen energy system

含氢能系统海上风电场的运行目标有2个：（1）海上风电场连接到主网（即并网模式），氢储能可在风力发电缩减期间充电，并在此期间之后放电，因此，海上风电场的发电量增加了。在这种情况下，海上风电场尝试在最大功率点跟踪（Maximum Power Point Tracking，MPPT）模式下工作，氢能系统将根据运行条件进行充电或放电；（2）海上风电场的运行环境恶劣，特别是台风天气将严重影响风机的安全。为了确保海上风机的安全，有必要在台风来临时改变偏航角，以将台风对风机的影响降至最低。然而，由于台风期间海上风电场将与电网断开（即在电网断开模式下），风机将停止发电，导致偏航电机失去其工作功率，无法改变叶片的方向，此外，风电场的停运使得受端电网出现供需平衡问题，由于传统柴油发电机启动到最大功率输出无法瞬时完成，使得受端电网可能出现大量停电现象。而安装在近海陆地的氢能系统可主动提供频率支撑，以确保在传统发电机组输出功率爬升时，系统供需平衡。

如图1所示，在风力发电机、氢能系统和受端电网的接口之间，需要大量功率变换器。背靠背式功率变换器通常配备永磁同步发电机（Permanent Magnet Synchronous Generator，PMSG），为风力发电机提供变速运行。同样，功率转换也适用于海上风电的高压直流输电系统。发电机侧功率变换器的作用是调节涡轮转矩，控制风力机采集，并将风力机的电能输送到海上交流母线。另一方面，海上高压直流输电（High Voltage DC，HVDC）电源变换器是将交流电源转换为HVDC形式，然后输送到受端电网。氢能系统侧的功率变换器是为了平衡风力供应和电网需求之间的有功功率平衡。

1）海上风机控制模型

风轮叶片从风中捕获能量并将其转换为旋转动能，然后机械能通过机械传动系统传输到发电机，通过发电机转化为磁场能，最后转化为电能。根据贝茨定律^[9]，风转子可以从风中提取的最大功率可表示为：

式中：

${P_{\rm{m}}}$ ——风轮的最大机械功率（W）；

$ \rho $ ——空气密度（kg/m³）；

R ——风轮叶片的半径（m）；

v ——风速（m/s）；

C_p ——风机的功率系数，其中$ {C_{\rm{p}}}{\text{ = }}f(\lambda ,\alpha ) $；

λ ——叶尖速比，$\lambda = {\omega _{\rm{m}}}R/v$；

${\omega _{\rm{m}}}$ ——风轮的机械角速度（rad/s）；

$ \alpha $ ——俯仰角（°）。

根据Betz极限（风机可从气流中提取的功率的理论极限），$ {C_{\rm{p}}} $的最大值为16/27$ \approx $0.593。考虑到空气涡流损失，实际值较小。

风机的输出功率是风速的非线性函数^[10-11]，主要由风机轮毂处的实际风速和风机的输出功率特性决定，如发电机、转子、齿轮箱和逆变器的运行效率^[12-13]。变桨距风机的输出功率特性可由以下几个参数决定：如v_ci、v_cr和v_co分别为切入风速、稳态风速和切出风速，P_r是额定输出功率。最常用简化线性公式来描述通用风机的输出功率^[14]：

式中：

${P_{\rm{e}}}(v)$——相对于风速v的风机的输出功率（W）。

对于可变桨距的风机，$ {P_{\rm{x}}} = {P_{\rm{r}}} $，对于固定螺距风力涡轮机，$ {P_{\rm{x}}} $可表示为：

式中：

P_co——v=v_co时风机的输出功率（W）。

本文将采用上述模型计算理论输出功率。

2）HVDC侧AC-DC/DC-AC的功率变换控制

HVDC侧AC-DC/DC-AC的功率变换器的主要任务是将交流电源整流到直流传输线路^[15-16]。若不考虑转换损失，传输风能为：

高压直流交流侧输出的有功功率和无功功率为：

假定${v_{{\rm{PC}}{{\rm{C}}_{\rm{d}}}}} = 0$，${v_{{\rm{PC}}{{\rm{C}}_{\rm{q}}}}} = \left| {{V_{{\rm{grid}}}}} \right|$。

式中：

$ \left| {{V_{{\rm{grid}}}}} \right| $ ——高压侧受端电网的电压幅值（p.u.）；

${v_{{\rm{PC}}{{\rm{C}}_{\rm{q}}}}}$、${v_{{\rm{PC}}{{\rm{C}}_{\rm{d}}}}}$ ——电网侧d轴和q轴转换到高压侧的等效电压（p.u.）；

${i_{{{\rm{G}}_{\rm{q}}}}}$、${i_{{{\rm{G}}_{\rm{d}}}}}$ ——DC-AC逆变器d轴和q轴等效电流（p.u.）。为维持电网侧电压，其控制为：

式中：

$ Q_{{\text{grid}}}^ * $——电网侧无功功率需求（Var）。

另一方面，$ {i_{{{\rm{G}}_{\rm{d}}}}} $可以通过PI调节器适当控制以稳定直流侧电压。

3）氢能系统的控制模型

氢能系统由一组电解槽、燃料电池和储氢罐组成^[17-18]。当风电场输出的电力超过电网需求时，电解槽将多余的电能产生氢气，然后储存在储罐中。当风力不足以支持电网要求时，燃料电池将储箱中储存的氢气用于补偿不足的功率。考虑到氢能系统运行的可行性和效率，本文中所有的电解槽和燃料电池都采用恒流运行模式。此外，本文还增加了一个超级电容器组，以缓冲来自风力的瞬态功率。

电制氢设备可用经验电流-电压关系来建模^[19]，其可表示为：

式中：

${U_{{\rm{cell}}}}$ ——单个电解槽电压（V）；

${U_{{\rm{rev}}}}$ ——可逆电解槽电压（V）；

r ——某工作温度下电解液欧姆电阻参数（Ω）；

${A_{{\rm{el}}}}$ ——电极面积（m²）；

${I_{{\rm{el}}}}$ ——电解槽电流（A）；

s、t ——电极过电压参数。

产氢量与电池中循环的电流成正比。法拉第效率（$ {\eta _F} $）定义为电解槽中实际产生的氢气量与理论最大值之间的比值：

式中：

$ {f_1} $、$ {f_2} $——法拉第效率参数。

利用法拉第效率，可计算出产氢量：

式中：

${m_{{\rm{H}}_2}}$ ——产氢量（mol/s）；

${S_{{\rm{cell}}}}$ ——每堆电解槽单元数；

$ z $ ——每摩尔水转移电子的摩尔数；

$ F $ ——法拉第常数（96 485 C/mol）。

电解槽电压为：

式中：

${V_{{\rm{el}}}}$——电解槽堆叠电压（V）。

电制氢装置的控制方框图如图2所示，电制氢设备产生的氢气需要储存起来，目前最常用储氢装置是高压气罐^[20]。使用合适的材料和尺寸，气态氢的储存可以在一个封闭的系统中进行，因此氢气可以在长时间内无损失地储存。

图  2  电制氢装置的控制方框图

Figure 2.  Block diagram of the control of electric hydrogen production plant

此外，罐内的氢气压力可作为测量氢气量的一种方法，储氢罐压力由范德华方程可得：

式中：

${p_{{\rm{sto}}}}$ ——储罐压力（atm）；

${R_{{\rm{gas}}}}$ ——通用气体常数0.082 06 atm·L/(mol·K)；

${T_{{\rm{sto}}}}$ ——储罐温度（K）；

${V_{{\rm{sto}}}}$ ——储罐体积（L）；

${m_{{\rm{sto}}}}$ ——储罐氢气消耗（mol）；

${p_{{\rm{tank}}}}$ ——储罐初始压力（atm）。

本文所提方法中，氢气作为压缩气体储存在储存罐中。电解槽或燃料电池的开关取决于储罐的电量状态。储氢罐的荷电状态${\rm{SOC}}_{\rm{H}}$（State of Charge）可表示为：

式中：

${p_{{\rm{st}}{{\rm{o}}_{\max }}}}$——储氢罐最大压力（atm）。

${{\rm{SOC}}_{\rm{H}}}$作为操作电解槽（充气）或燃料电池（放电）的参考值，其取值范围为（0,1）。

为了避免过充氢或深度放电，并保持氢能系统的必要备用容量，应特别注意将${{\rm{SOC}}_{\rm{H}}}$调节在适当的工作范围内。本文从0~1将整个${{\rm{SOC}}_{\rm{H}}}$范围分为五个子区间，其中，${{\rm{SOC}}}_{{\rm{H}}，\rm{max}}$为${{\rm{SOC}}_{\rm{H}}}$的最大工作极限，通常设置为略小于氢储能的允许最大${{\rm{SOC}}}_{{\rm{H}}，\rm{max}}$以避免过充；${{{\rm{SOC}}}}_{{\rm{H}}，\rm{min}}$为SOC_H的最小工作极限，通常设置为略大于氢储能的允许最小${{\rm{SOC}}}_{{\rm{H}}，\mathrm{min}}$以避免深度放电。在并网模式和电网断开模式下，氢储能的${{\rm{SOC}}_{\rm{H}}}$均允许在规定范围${{\rm{SOC}}_{{\rm{H}},{\rm{ref}}}}$内，在电网断开模式下的紧急情况下，${{\rm{SOC}}_{\rm{H}}}$允许在紧急范围内。${{\rm{SOC}}_{{\rm{H}},\;{\rm{ref}}}}$是并网模式下稳定经济运行的参考${{\rm{SOC}}_{\rm{H}}}$。在任何情况下SOC_H均不能大于${{\rm{SOC}}}_{{\rm{H}}，\rm{max}}$或小于${{\rm{SOC}}}_{{\rm{H}}，\rm{min}}$，以防止氢储能因过度充氢或深度放电而损坏。根据这些限制设置开关规则来控制电制氢设备或燃料电池的激活（ON）和关闭（OFF）。

单燃料电池电压课表为：

式中：

${E_{{\rm{nernest}}}}$——电池可逆电压（V）；

${V_{{\rm{act}}}}$ ——激活超电势；

${V_{{\rm{ohmic}}}}$ ——欧姆超电势；

${V_{{\rm{con}}}}$ ——浓差超电势。

${V_{{\rm{act}}}}$、${V_{{\rm{con}}}}$和${V_{{\rm{ohmic}}}}$与燃料电池电流有关。假设燃料电池的输出是电流控制的，多个单电池单元串联堆叠以增加功率输出。该单元数的堆叠电压为：

由于FC需要氢气发电，因此FC输出电流的控制应与氢量相关：

式中：

${m_{{{\rm{H}}_{2{\rm{use}}}}}}$ ——耗氢量（mol/s）；

${m_{{{\rm{O}}_{2{\rm{use}}}}}}$ ——耗氧量（mol/s）；

$ F $ ——法拉第常数（96 485 ℃）。

本例中FC的控制是根据所需要的功率来设置FC电流，该模型将计算氢气储罐的氢气消耗量。

超级电容器又称电双层电容器，具有双层结构来充放电能量。由于不涉及电化学反应，超级电容器的可逆性比任何二次电池都快得多。超级电容器储能由串联和并联连接的电池组合组成，以实现所需的系统电压和电容额定值。一个堆叠中串联单元的数量由所需的最大电压决定。因此，超级电容电压为：

由并联堆栈数决定的整体超级电容器组电流：

式中：

${I_{\rm{t}}}$——堆叠单元的端口电流。

通过改变总支路电流可以控制流入超级电容器的功率：

超级电容器的电荷状态（SOC_sc）可表示为：

式中：

${V_{{\rm{SC}}\min }}$、${V_{{\rm{SC}}\max }}$——超级电容器的最小电压和最大电压（V）。

被控电流（I_t）的输入和输出会改变$ {V_{{\rm{SC}}}} $，进而改变$ {{\rm{SOC}}_{{\rm{SC}}}} $。

风电场一般由风电场监督控制系统控制，该系统为每台风力机设置有功功率指令。在大多数运行期间，海上风机以MPPT运行，以最大限度地获取风能。当台风期间出现功率不平衡时，氢能系统对风电场输出功率与受端电网负荷需求之间的不平衡功率进行补偿。然而，即使氢能系统在大多数情况下可以发挥这一作用，也可能有一些氢能系统要么是因为储存罐是空的或满的，要么是整个HMS正在进行维护而无法正常运行。此时，风电场监督控制系统应控制海上风电改变其输出功率以满足电网要求。通常，含氢能系统的海上风电场以并网模式工作，捕捉风能、发电并通过输电系统提供负荷。当台风来临时，它将切换到电网断开模式，以保护海上风电机组免受安全事故的影响，此外还要通过储能释放有功，给予受端电网功率再平衡时间。为了满足这一运行要求，本文设计了1种台风期间海上风电与氢能系统的协同控制方法，台风期间海上风电与氢能系统的协同控制协调控制图如图3所示。

图  3  海上风电和氢能系统的协同控制图

Figure 3.  Collaborative control diagram of offshore wind power and hydrogen energy system

在非功率限制运行的情况下，海上风电以MPPT模式工作，最大限度地捕获风能，BESS根据其SOC是否存在任何台风警报信息进行充电或放电。当没有台风警报信息时，BESS将以预定的适当功率P_dis放电，直到其SOC达到SOC_low。当有台风警报信息时，BESS将以预定的适当功率P_ch充电，直到其SOC达到SOC_high，以便在电网断开模式下独立向本地电力负荷供电，协同控制流程图如图4所示。

图  4  台风期间海上风电与氢能系统的协同控制流程图

Figure 4.  Collaborative control flow chart of offshore wind power and hydrogen energy system during typhoon

由图4可知，在正常运行条件下电网调度中心为海上风电与氢能系统设置有功功率指令$P_{{\rm{grid}}}^ *$和无功功率指令$Q_{{\rm{grid}}}^ *$。HVDC有功功率${P_{{\rm{HVDC}}}}$、无功功率输出${Q_{{\rm{HVDC}}}}$和氢能系统的有功功率输出${P_{\rm{H}}}$协调，使整个系统输出（风电场加上氢能系统）尽可能地跟踪和接近受端电网负荷需求（$P_{{\rm{grid}}}^ *$和$Q_{{\rm{grid}}}^ *$）。当$Q_{{\rm{grid}}}$控制时，陆上HVDC有功功率输出为：

当发生台风极端天气时，氢能系统可平衡${P_{{\rm{HVDC}}}}$和$P_{{\rm{grid}}}^ *$的有功功率差。其具体控制为：

式中：

$P_{\rm{H}}^ *$——氢能系统输出功率的参考值（W）。

电解槽、燃料电池和超级电容器系统的有功功率命令分别为：

式中：

$ P_{{\text{EL}}}^ * $、$ P_{{\text{FC}}}^ * $——电解槽和燃料电池的恒功率（W）。

在台风条件下，电解槽吸收的多余功率范围取决于氢荷电状态（${{\rm{SOC}}_{\rm{H}}}$）以及电解槽额定功率。当由于这些原因，多余的风电不能被电解槽完全吸收时，应对风电功率进行限制。在这方面，应指导风力涡轮机增加其桨距角，以减少功率采集（减载）。当需要约束风电场功率时，控制系统将设置风电场功率为：

其中$ {P_{{\text{Hlim}}}} $为电解槽组可使用的最大功率限制。若储氢满，则设为0。然后分配到每个风机。一般情况下，风速越大，风力机的分配系数加权越高。给定风速下，每台风力机的分配因子可表示为：

式中：

$W({V_\text{ω} })$ ——各级风速的权重因子；

$N({V_\text{ω} })$ ——风电场内以该风速运行的风力机数。

因此，式（25）中分母的总和包括所有可用的风机。利用分配因子，各风力发电机设定点为：

由此，得到发电机侧电磁转矩为：

式中：

P ——磁极数；

${\omega _{\rm{r}}}$ ——风力机电转子转速（rad/s）。

台风来临时，海上风电场与主电网断开，风机逐渐关闭。氢能系统负责确保发电和消耗（本地负荷）之间在任何时刻的功率平衡，此外，还要保障受端电网的有功平衡，对于交流电力系统，发电和负载之间的功率平衡表示为恒定的电压幅值和频率。频率控制器通过调节氢能系统的输出有功功率将频率保持在给定参考值f_ref，例如50 Hz，电压调节器通过调节氢能系统的输出无功功率将电压幅值U保持在给定参考值U_ref。有功和无功功率的参考值，即P_ref和Q_ref，关键是如何确定这两个功率参考值以保持电压和频率恒定。

本文设计了本地自适应模糊推理系统，实时调整氢能系统的有功无功功率输出，以消除海上风电场逐步脱网对受端电网电压频率的影响。与PI控制技术相比，自适应模糊控制技术具有灵活性强、鲁棒性好、适用于工程应用等优点。所提自适应模糊推理系统共有2个输入量和1个输出量，输入量分别为受端电网的电压偏差和频率偏差，输出为BESS的有功无功输出。模糊推理系统的基本控制原理为：（1）将$ \Delta f $和$ \Delta U $通过模糊化转化为模糊变量；（2）模糊器是利用隶属函数提取有效的信息。本文选择三角形隶属度函数以满足快速调整需求。电压误差和频率误差的三角形隶属函数图如图5所示。

图  5  电压偏差和频率偏差的三角形隶属函数图

Figure 5.  Triangular membership function diagram of voltage deviation and frequency deviation

由图5可知，每个隶属度函数都定义了自己的权重，并给出了语言变量。语言变量进入模糊推理系统（FIS）。FIS中定义的规则库可以给出推理结果。例如，电压误差NB和误差率NB可以得到模糊输出NB。最后，在去模糊化后，得到非模糊输出。此外，本文针对模糊推理系统还设计了自适应规则调整因子$ \alpha $，使控制器能够基于$ \Delta f $和$ \Delta U $自动调整模糊规则，以提高控制器的性能。自适应律描述为：

不同$ \alpha $值会产生不同的控制规则。

为了验证所提方法的有效性，本文以广东某实际海上风电场为仿真对象，在Matlab中通过仿真测试了所提方法在台风条件下的控制效果。该风电场采用的直驱风机，额定容量为10 MW。表1为海上风电与氢能系统的相关参数。

1）海上风电机组含减载控制

台风来临前夕时，海上风速通常较高，此时，海上风电通常以MPPT模式运行，而氢能系统可用来调节台风引起大风条件下的功率平衡。根据刚才提到的运行原理，最终控制目标是使含氢能系统的海上风电场功率输出负荷遵从受端电网的有功和无功需求。本文采用通过风力减载控制以解决氢能过充问题。风电场在运行过程中可能发生超过受端电网负载需求或氢储能较慢时，风电场减载控制将减少其输出以遵循电网指令。图6为台风前夕含氢能系统海上风电场的风电场出力、氢储能SOC和受端电网有功需求图。

图  6  台风前夕含氢能系统海上风电场的风电场出力、氢储能SOC和受端电网有功需求图

Figure 6.  Diagram of wind farm output, hydrogen energy storage SOC and active power demand of the receiving-end grid for the offshore wind farm with hydrogen energy system before typhoon

由图6可知，在1 000 s左右，储氢罐已满，控制系统开始降低风电场输出以跟踪受端电网的有功需求。因为没有多余的能量产生，超级电容器组的SOC不再达到上限水平。因此，在整个测试期间，受端电网实际有功需求与实时需求重合。

2）氢储能存氢不足时

为了验证所提系统中氢气耗尽对受端电网运行的影响。图7为氢气不足时受端电网有功、无功和风电场功率输出图。图8为氢能系统的SOC图。

图  7  氢气不足时受端电网有功和风电场功率输出图

Figure 7.  Diagram of active power of receiving-end grid and power output of wind farm when hydrogen is insufficient

图  8  氢能系统的SOC图

Figure 8.  SOC diagram of hydrogen energy system

从图7(a)可以看出，1 000 s后风电功率低于受端电网功率需求。由于风电场和氢能系统都不能完全支持电网有功功率。

图8(a)和图8(b)分别为电解槽/燃料电池系统和超级电容器系统的功率。在最初三分之二的总运营期间，氢能系统在风力发电和电网需求之间保持平衡。后来，由于氢气耗尽，平衡机制被关闭。从图8(c)和图8(d)可以看到储氢和超级电容器的SOC下降到最低水平。

当台风来袭时，海上风电场逐步关闭，造成的功率缺额由氢能系统提供。图9为海上风电在台风条件下的输出特性图，其截止风速为20 m/s。

图  9  台风条件下海上风电的输出曲线

Figure 9.  Output curve of offshore wind power under typhoon conditions

由图9可知，海上风电在25 min内从额定值降至零。图10为风-储综合系统的聚合功率输出，以及储能系统的功率与能量。

图  10  海上风电与BESS平抑效果图

Figure 10.  Smoothing effect of offshore wind power and BESS

图10结果表明，储能系统对风电功率波动的平抑效果明显。在台风过境期间，储能系统能够事先充氢，在发生功率缺额时快速放电（功率为正表示放电），实现风-储综合系统的功率平抑控制，使系统整体的功率输出更接近给定值，降低了其对电网稳定运行的不利影响。在储能出力过程中，其功率与能量均运行于安全范围内。

针对台风期间海上风电场与主网主动断开时，对受端电网造成不利影响。为了实现台风期间海上风电友好接入，考虑到氢储能具有储存效率高、排放低和应用广泛等优点，本文提出了一种海上风电场与氢气管理系统之间的协同控制方法，台风临近时期，电池储能系统可在正常运行下最大限度地利用风能发电，并在台风过境期间作为海上风电的备用电源，以减小其对受端电网的不利影响，有效平移海上风电输出的波动性。首先详细介绍了海上风电场与氢能系统的物理建模方法及控制模型，并根据台风期间说明了二者之间的协同控制策略。最后，通过仿真验证了所提方法使海上风电场能够更灵活且友好地满足台风期间的并网运行。此外，氢储能系统可在正常运行下最大限度地利用风能发电，并在台风期间作为海上风电的备用电源，以减小其对受端电网的不利影响。仿真结果表明，储能系统对风电功率波动的平抑效果明显。在台风过境期间，储能系统能够事先充氢，在发生功率缺额时快速放电，实现风-储综合系统的功率平抑控制，使系统整体的功率输出更接近给定值，降低了其对电网稳定运行的不利影响。在储能出力过程中，其功率与能量均运行于安全范围内。