-
在气候变暖的背景下，随着经济社会的发展，人们对能源需求和依赖程度不断提高，对能源的使用方式和利用效率提出了更高的要求。在风能、太阳能等清洁能源高速发展的今天，电力系统的能源结构发生了巨大变革，加之因提高能源利用效率而引发的电力市场改革不断深入，这些给电网安全运行增加了较大的不确定性，同时带来了新的挑战。然而，由于社会运转速度的不断加快和信息量的膨胀，使准确的用电量预测变得愈加困难[1]。因此，准确开展电网用电量的预测，掌握电网安全运行区间是新形势下电网安全运行的基础[2]。
电网用电量作为电网系统中的一个至关重要的变量，对于指导电力系统规划、运行、控制、稳定都有重大的影响。由于电网系统是一个复杂的、非线性的耦合系统，用电量的时间序列一般也具有非线性、非平稳的特点。传统电力系统短期用电量预测方法主要包括时间序列[3]、回归分析[4]、灰色模型[5]、相似日、负荷求导等；但传统预测方法一般忽略了电网系统具有的随机、突发和混沌等特性，导致预测结果与实际需求有一定的差距。近年来，随着机器学习、深度学习应用领域的拓展，以神经网络、支持向量机[6-8]、小波分析等为代表的机器学习方法[9-10]更多地在短期用电量预测中得到应用。神经网络这种类型的机器学习方法的优势在于：不需要对输入变量做复杂的假设，可以模拟多个变量；利用输入变量在训练过程中，通过学习来抽取和逼近隐含的输入和输出变量之间非线性关系[11]。
由于传统时间序列分析方法要求数据的线性和平稳性，因此，很难得到具有明确物理意义的结果。为有效解决这一问题，Huang等[12]最早提出经验模态分解（Empirical Mode Decomposition, EMD）的方法，可以将复杂的时间序列分解为具有不同特征尺度的时间序列，即本征模函数（Intrinsic Mode Function, IMF），得到的趋势项是一个单调函数或仅有一个极值的函数。但是，由于有些信号具有间歇性，出现模态混合，导致分解出的IMF分量缺乏一定的物理意义。Wu和Huang[13]在EMD方法的基础上，发展了集合经验模态分解（Ensemble Empirical Mode Decomposition, EEMD）对EMD方法进行了改进，在原始信号中加入白噪声并进行多次EMD分解，以消除EMD中存在的模态混合。
EEMD是一种近年来发展的时间上局部的自适应时间序列分析技术，适用于分析非线性、非平稳的时间序列[14]。近年来，国内学者应用EEMD方法开展了有关气候变化的研究工作，如旱涝变化[15]、热带风暴[16]及其影响机制、节气变化[14]、气温[17-18]和降水变化[19]、全球气候模式的模拟研究[20]。同时，EEMD方法在风电场风电功率预测[21-22]、光伏电站短期发电功率预测[23-24]及径流的变化研究[25]中也得到了较好的应用。
近年来，国内学者利用EEMD方法开展电网负荷和电量预测研究[26-27]，并取得了较多有意义的成果，组合预测方法已经被证明是一种可以提高预测精度的有效方法[28-29]。有学者探索了EEMD-BP方法在电网负荷和用电量预测中的应用，研究表明，EEMD-BP组合预测方法比BP预测方法可有效减小预测误差[30]。众多学者的研究表明，用电量受经济发展水平、气象因子、电价、节假日、工农业结构等众多因子的影响[31]，但气象因子的影响尤为显著[32-36]。前人的研究多集中在EEMD与其他方法组合预测对负荷和用电量预测的改进效果，但气象条件在组合预测中对预测精度的影响分析相对较少。因此，在前人研究的基础上，本文利用华中电网某市2017年逐日电量和气象数据，建立了基于EEMD-BP方法的日用电量预测模型，并对模型的回归和预测结果进行分析，以期为改进和完善短期用电量预测方法提供参考和指导。
-
EEMD算法与EMD算法大致相同：给定原始信号x(t)，通过将x(t)引入白噪声，采用EMD算法对引入白噪声的原始信号进行多次分解，将分解后的IMF向量和剩余分量求其平均。EEMD算法基本步骤[25]如下：
1）确定好已初始化的EMD算法迭代次数M和第m次实验和加入白噪声n(t)后的信号y(t)：
$$ y(t)=x(t)+n(t) $$ (1) 2）对y(t)信号进行EMD分解，得出各阶IMF分量和一个剩余分量：
$$ y\left(t\right)=\displaystyle \sum\limits _{i=1}^{m}{c}_{i}+{r}_{n} $$ (2) 3）若m<M时，m＝m+1。重复式（1）、式（2），对原始信号x(t)加入不同白噪声ni(t)后得到各个IMF分量和各个剩余分量。不满足则执行式（4）。加不同白噪声后的信号：
$$ {y}_{i}\left(t\right)=\sum _{j=1}^{m}{c}_{{i},{j}}+{r}_{n} $$ (3) IMF分量ci, m(t)以及剩余分量rn, m(t)分别为：
$$ c_{{i}, {m}({t})}=h_{{j}, {m}({t})}, r_{{n}, {m}({t})}=r_{{n}-1, {~m}({t})}-{c}_{{n}, {m}({t})} $$ 4）经过M次EMD分解，对各阶IMF分量和剩余分量求整体平均值得：
$$ \overline{{{c}}_{{i}}}\left({t}\right)=\displaystyle \sum\limits _{{m}=1}^{{M}}{{c}}_{{i},{m}}\left({t}\right)/{M},\overline{{{r}}_{{n}}}\left({t}\right)=\displaystyle \sum\limits _{{m}=1}^{{M}}{{r}}_{{n},{m}}\left({t}\right)/{M} $$ (4) 输出的$\overline{{{c}}_{{i}}}\left({t}\right)$和$\overline{{{r}}_{{n}}}\left({t}\right)$分别为各阶IMF分量和剩余分量。
BP方法（Back-Propagation）也叫误差反向传播算法，是一种具有3层或3层以上的前馈神经网络，BP神经网络有1个输入层，1个或多个隐含层和1个输出层，上下层之间的各神经元实现全连接，具体算法参考文献[11]的研究。
基于气象因子的EEMD-BP用电量预测模型的研究思路：首先将用电量序列采用EEMD方法进行分解，获得多个本征模函数（IMF）和残差；将本征模函数按高频分量、周期分量及低频分量采用BP神经网络分别构建不同的IMF和残差的预测模型，其中低频分量中叠加气象因子；最后，将BP模型预测的结果进行累加即可得到最终的预测用电量。
本文所用的电力数据为国家电网华中分部调度控制中心提供的华中某市2017年逐日用电量数据。气象数据时段同为2017年，要素包括逐日的平均温度、最高温度、最低温度、降水量、相对湿度、气压、风速等，国家气象观测站包括华中某市下辖的各县（市），数据来源于湖北省气象信息与技术保障中心。最终以各县（市）国家气象观测站不同要素的算术平均表征该市的气象要素值。用电量和气象数据均经过严格的质量控制。
-
以华中某市2017年逐日电网用电量为初始序列，加入该序列标准偏差0.01倍振幅的白噪声进行EMD分解，得到8个IMF，每次都增加同样振幅但数值不同的白噪声序列重复上述过程100次，最后将100次结果相应的IMF各自集合平均得到8个IMF及余项，结果如图1所示。可以看出，频率依次减小，周期逐渐增大，平稳性得到改善。IMF1~IMF2叠加代表随机分量，表现出较强的非平稳性；IMF3~IMF5叠加代表周期分量；IMF6~IMF8及剩余项叠加为趋势分量，平稳性和规律性增强。
Figure 1. Decomposition results of electricity consumption series in 2017
随机分量是分解后高频部分的总和，体现了用电量变化的随机性，该部分很难建立模型进行预测，属于不可预测分量。周期分量反映了用电量周、月、季节为周期变化的分量，在预测中可直接外推，属于稳定分量成分。趋势分量是低频分量的总和，反映了气象因素等慢变相关因素对用电量的影响，该部分属于可预测分量，可以通过建立合适的模型进行预测。
为分析用电量不同频域分量与气象因子的关系，表1给出了气象因子同用电量分解后各IMF及余项的相关系数统计。可以看出，用电量实况值与逐日平均气温、最高气温和最低气温存在显著的正相关，相关系数分别为0.47、0.47和0.45，均通过信度为0.01的显著性检验，与气压存在显著的负相关、相关系数为−0.4；而与降水等级、相对湿度和风速的相关并不明显。
分量类型 序列 平均气温/℃ 最高气温/℃ 最低气温/℃ 降水等级 气压/hPa 相对湿度/% 风速/(m·s−1) — 原始序列 0.47** 0.47** 0.45** −0.10 −0.40** 0 −0.10 高频分量 IMF1 0.06 0.05 0.03 0.00 0.00 0.00 −0.18** IMF2 0.01 0.01 0.00 0.00 0.05 0.00 −0.10 — IMF3 0.22** 0.21** 0.20** −0.10 −0.20** 0.10 0.01 周期分量 IMF4 0.14* 0.15* 0.14* −0.10 −0.20** −0.10 −0.10 IMF5 −0.20** −0.20** −0.30** −0.20** 0.19** −0.40** 0.00 — IMF6 0.33** 0.29** 0.39** 0.07 −0.30** 0.36** 0.04 低频分量 IMF7 0.32** 0.26** 0.37** 0.06 −0.10 0.14* 0.03 IMF8 0.88** 0.86** 0.89** 0.17* −0.80** 0.47** −0.10 — 余项 0.40** 0.42** 0.39** 0.11 −0.60** 0.37** 0.00 注：*表示通过信度为0.01的显著性检验；**表示通过信度为0.001的显著性检验。降水等级分级：无雨为0；0.1～9.9 mm为1；10.0～24.9 mm为2；25.0～49.9 mm为3；50 mm以上为4。 Table 1. Correlation coefficients of meteorological factors with IMF and residuals
高频分量中，IMF1和IMF2分量与各气象因子没有相关关系，仅与风速要素存在明显的负相关。周期分量中IMF3~IMF4与用电量实况序列的特征比较一致，与平均气温、最高气温、最低气温存在正相关，与气压存在负相关，相关系数明显减小，但均通过了显著性检验；与降水等级、相对湿度和风速的关系并不密切。IMF5分量与温度、降水等级、相对湿度呈显著负相关，而与气压呈显著正相关。低频分量IMF6~IMF8和余项除与平均气温、最高气温、最低气温存在显著的正相关、与气压存在显著的负相关之外，与相对湿度也存在明显的正相关，IMF8分量与气象因子的相关关系较其他序列明显提高，相关系数分别为0.88、0.86、0.89、−0.80、0.47，均通过了信度为0.01的显著性检验。因此，在利用EEMD-BP建立预测模型时，选用相关性通过显著性检验的平均气温、最高气温、最低气温、气压和相对湿度这5个气象因子。
-
为检验预测模型的效果，首先对模型的回归效果进行分析。本文所构建的双隐含层BP神经网络模型，输入层为前1天用电量，输出层为当日用电量。BP-QX为叠加气象因子的神经网络模型，输入层除前1天的用电量，还包含了当日的平均气温、最高气温、最低气温、气压和相对湿度，输出层同为当日用电量。
图2给出了利用BP、BP-QX（叠加气象因子）和EEMD-BP、EEMD-BP-QX模型回归用电量序列。可以看出，利用BP、EEMD-BP模型回归得出的用电量序列可较好地拟合原始用电量序列，相关系数为0.94、0.98，但依然存在一定的误差；引进气象因子后，BP-QX、EEMD-BP-QX回归用电量序列与原始序列的相关性有所提高，分别为0.98、0.99，同时误差进一步缩小。
Figure 2. Regression analysis of electricity consumption series
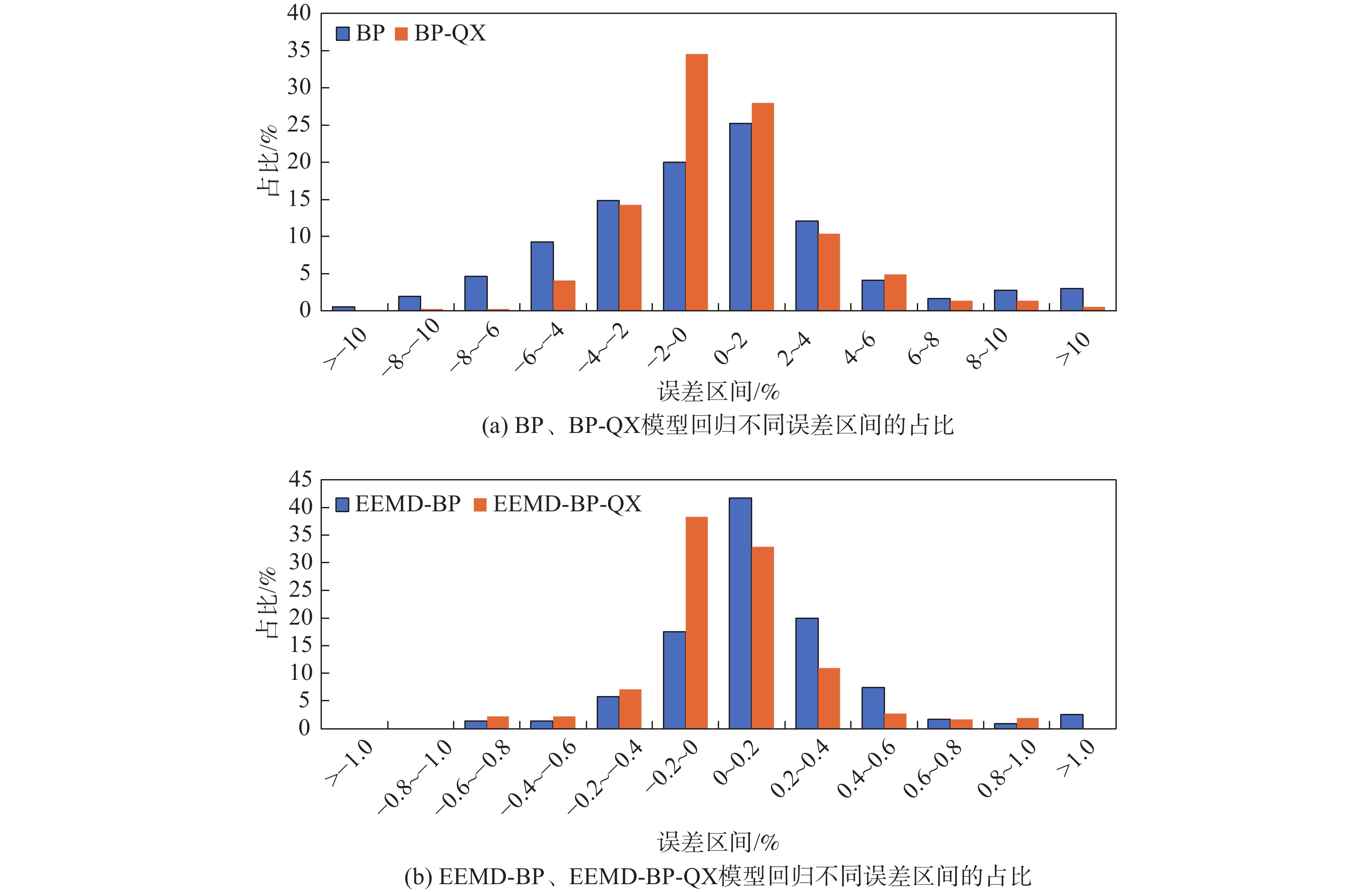
为了进一步分析不同预测方法及其叠加气象因子后回归效果，图3给出了模型回归不同误差区间的占比。利用BP模型回归得出的用电量与原始用电量之间误差在4%以内天数占全年的72.0%，其中误差在2%以内的占比为45.2%；误差在10%以上的占比为3.6%（图3（a））。全年回归用电量的平均绝对误差为3.2%，均方根误差为4.83；其中最大相对误差为27.3%，出现在8月8日。在BP回归模型的基础上，叠加气象因子之后的回归效果得到了改善，误差在4%以内的天数占全年的87.0%，较直接利用BP模型得出的相同误差占比提高了15.0%，其中误差在2%以内的占比提高了17.2%；而误差在10%以上的天数占比减小为0.6%。全年回归用电量的平均绝对误差在2.1%，均方根误差为2.82；其中最大误差为16.3%，出现在1月28日，而8月8日的相对误差减小为0.87%。通过对比发现，引进气象因子后，BP方法模拟得到的用电量有了较为明显的改进，但误差依然较大，很难满足用电量精细化预测的需求。
Figure 3. Proportion of different error intervals in regression analysis
对比发现，利用EEMD-BP方法得出的回归序列与原电量序列的相对误差得到了明显的改进（图3（b））。绝对误差在0.4%之内的天数占全年的88.0%，其中误差在0.2%之内的天数占比为62.2%。绝对误差在1%以上的天数占比为2.4%，绝对偏差为0.22%，均方根误差为0.34，最大相对误差为2.25%。可见，EEMD-BP方法对用电量模拟的精度有了大幅提高，尤其是BP方法中误差较大的6月4日、8月8日、8月12日、8月29日，相对误差由原来的17.8%、27.3%、17.4%、26.2%减小至0.7%、−0.38%、−0.09%、0.12%。
在EEMD-BP方法的基础上，进一步分析了气象因子对用电量预测模型的影响。引进气象因子以后，相对误差有了明显的降低，尤其是在夏季和冬季，因为冬夏两个季节的气象条件对用电量的影响尤为明显。1月28日，EEMD-BP方法预测的用电量相对误差为2.25%，EEMD-BP-QX预测的用电量相对误差减小至1.81%，气象条件对用电量预报模型的影响一直持续到1月30日。绝对偏差、均方根误差和最大相对误差也有一定的减小。可见，气象条件对EEMD-BP用电量预测模型至关重要。
-
通过以上的分析，叠加了气象因子的EEMD-BP方法构建用电量预测模型可以有效地提高预测精度。为进一步分析EEMD-BP以及气象条件对用电量的预测效果，从BP和BP-QX的回归序列中，选取模拟相对误差>10%的日期为预测对象，共计14 d，具体日期选择如表2所示，剩余日期的用电量和气象因子为建模对象。具体方法选取模拟相对误差≤10%的日期构建双隐含层BP神经网络模型，输入层为前1天用电量和当日的平均气温、最高气温、最低气温、气压和相对湿度，输出层为当日用电量；在此神经网络模型的基础上，根据模拟相对误差>10%日期的前1天用电量和当日气象因子作为预报因子，预测当日的用电量。
日期 实际电量/
GWhBP预测电量/
GWh相对误差/
%BP-QX预测电量/
GWh相对误差/
%EEMD-BP预测电量/
GWh相对误差/
%EEMD-BP-QX预测电量/
GWh相对误差/
%0125 17.959 20.757 15.6 20.250 12.80＋ 18.056 0.50 17.997 0.21＋ 0128 15.224 18.406 20.9 18.934 24.30 15.499 1.82 15.361 0.91＋ 0501 18.211 19.224 5.6 17.429 −4.30＋ 18.258 0.22 18.203 −0.04＋ 0530 19.577 18.594 −5.0 19.801 1.10＋ 19.603 0.13 19.618 0.21 0604 18.638 19.492 4.6 19.505 4.60 18.682 0.23 18.673 0.18＋ 0703 25.584 18.857 −26.3 21.902 −14.30＋ 25.528 −0.21 25.597 0.05＋ 0709 20.798 25.535 22.8 21.612 3.90＋ 20.753 −0.22 20.835 0.17＋ 0803 29.987 20.917 −30.2 25.051 −16.50＋ 30.916 3.10 30.042 0.18＋ 0808 23.425 29.566 26.2 22.209 −5.20＋ 23.419 −0.02 23.446 0.09 0812 22.596 23.372 3.4 22.498 −0.43＋ 22.632 0.16 22.589 −0.03＋ 0829 21.084 22.539 6.9 20.607 −2.30＋ 21.037 −0.22 21.104 0.09＋ 0910 19.551 21.176 8.3 20.151 3.10＋ 19.609 0.30 19.603 0.26＋ 1001 16.809 19.468 15.8 19.606 16.60 16.961 0.91 16.884 0.44＋ 注：＋表明叠加气象因子后相对误差减小。 Table 2. Statistics of power forecast (unit: 10 MWh) and relative error (%) by different models
从表2可以看出，利用BP回归模型预测的用电量与实况误差较大，8月3日预测用电量较实际用电量偏少了9071 MWh，8月8日预测电量则偏高了6142 MWh，相对误差范围在−30.2%～26.2%。引进气象因子后，除了1月28日（偏高528 MWh）、10月1日（偏高138 MWh）外，其他日期预测的用电量与实况的误差均有所减小，尤其是7月3日、7月9日、8月3日和8月8日，误差分别减小了3046 MWh、3923 MWh、4134 MWh和4926 MWh，相对误差分别减小了11.9%、18.9%、13.8%和21.0%。
利用EEMD-BP得出了预测误差有了明显的减小，除了1月28日（偏高275 MWh）、8月3日（偏高928 MWh）和10月1日（偏高153 MWh）偏差相对较大外，其他日期预测误差均在100 MWh内，相对误差控制在0.5%以内。引进气象因子后，使得预测电量与实况的误差有了进一步的减小，尤其是8月3日、1月28日，误差分别减小了873 MWh和138 MWh，预测相对误差分别由3.1%减小至0.41%、1.8%减小至0.9%。
为进一步比较不同模型对用电量预测准确率的影响，分析了不同方法之间对预测准确率的影响差异。相对BP模型，BP-QX模型提高幅度在1.34%～5.72%（除1月28日和10月1日）；而7月3日、7月9日、8月3日和8月8日这4日预测准确率提升幅度尤为明显，分别达到16.15%、24.42%、19.76%和28.5%。EEMD-BP较BP和BP-QX而言，用电量的预测准确率均有所提高，1月25日、1月28日、7月3日、7月9日、8月3日、8月8日和10月1日这7天用电量的预测准确率均在10%以上，其中7月3日、7月9日、8月3日和8月8日这4日达到或超过30%。EEMD-BP-QX与EEMD-BP的结果比较类似，用电量的预测均高于BP和BP-QX；除了5月30日和8月8日预测准确率有微弱的减小，其他日期的用电量预测均高于EEMD-BP，其中8月3日和1月28日尤为明显，分别提高了3.01%和0.92%。
-
电力系统海量化数据为用电量特性分析和高精度的预测模型提供了保障，但传统的神经网络预测模型往往由于过拟合问题反而会降低预测准确率[10]。因此，本文在充分考虑气象条件前提下，将EEMD分析方法引入用电量预测研究中，通过频域分解的方法提取不同频率的分解结果与气象数据之间隐含的非线性关系，探究用电量数据深层的变化规律，实现对用电量的精准预测。主要的研究结论如下：
1）用电量与逐日平均气温、最高气温和最低气温存在显著的正相关，相关系数分别为0.47、0.47和0.45，与气压存在显著的负相关、相关系数为−0.4；而与降水等级、相对湿度和风速的相关并不明显。用电量原始序列经EEMD分解后低频分量和余项与平均气温、最高气温、最低气温和相对湿度存在显著的正相关，与气压存在显著的负相关之外。
2）利用BP模型得出的预测电量与实况之间误差在4%以内天数占全年的72.0%，其中误差在2%的占比为45.2%。叠加气象因子之后的BP回归效果得到了改进，误差在4%的天数占全年的87.0%，较直接利用BP模型得出的4%之内相对误差提高了15.0%，其中误差在2%以内的天数提高了17.2%。利用EEMD-BP方法得出的回归序列使得相对误差得到了明显的改进，误差在0.4%之内的天数占全年的88.0%，其中误差在0.2%之内的天数占比为62.2%；引进气象因子后，在相对误差相对较大的日期，预测准确率有了进一步提升，尤其是在夏季和冬季。
3）相对BP模型，BP-QX模型大部分天数的预测准确率均有不同程度的提高，提升幅度最高可达28.5%。EEMD-BP较BP和BP-QX而言，用电量的预测准确率提升幅度均在10%以上，其中部分天数达到或超过30%。在EEMD-BP的基础上，EEMD-BP-QX模型用电量的预测准确率也有一定程度的提升。
通过比较不同模型的模拟精度可以发现，EEMD-BP相较于BP方法，模拟精度得到了较大的提高，可能原因在于利用BP对用电量序列进行预测时存在一定的累积误差。而EEMD可以将原始非平稳电力负荷序列分解成一系列复杂度差异明显的子序列，和原序列相比，这些子序列的局部用电量特性更加明显，更有利于预测[27]。其次，在分解后的低频分量中叠加气象因子对序列进行预测，更有利于提高用电量预测的精度。由于用电量本身的不确定性和复杂性，准确的用电量特性分析和预测模型建立是提高预测精度的关键所在[37]。因此，未来电力系统用电量预测方法的关键在于提高准确性和实时性，以达到智能电网对用电量精细化预测的要求。当然，本文仅利用2017年逐日用电量序列进行建模和检验，用电量序列的长度是本文的短板所在。后期会延长用电量的序列和增加不同的地区，进一步探讨气象因子对用电量预测的影响，以便验证构建的模型在其他年份或地区的适用性和预测精度。
Application of EEMD-BP Method Based on Meteorological Factors in Grid Electricity Consumption Forecast
doi: 10.16516/j.ceec.2024.1.13
- Received Date: 2023-05-15
- Rev Recd Date: 2023-06-16
- Available Online: 2023-09-15
- Publish Date: 2024-01-10
-
Key words:
- ensemble empirical mode decomposition /
- electricity consumption /
- meteorological factors /
- refined forecast /
- regression model
Abstract:
| Citation: | ZHANG Zhen, XIAO Ying, REN Yongjian, et al. Application of EEMD-BP method based on meteorological factors in grid electricity consumption forecast [J]. Southern energy construction, 2024, 11(1): 122-132 doi: 10.16516/j.ceec.2024.1.13
|
DownLoad:
