-
由于传统化石能源的过度开采与使用导致气候变化和环境污染等问题日益严重，使得能源开发转向可再生的绿色能源[1]。作为新型清洁可再生能源，风力发电的发展备受瞩目[2]。随着国内风电技术的进步，风电机组逐渐向大容量、低成本、高可靠性方向发展。主轴轴承是风电机组传动支撑的关键部件[3-4]，其配置选型也迎来相应的挑战，围绕主轴轴承工程应用技术的探讨开始受到行业工程师和专家学者的关注。应用在风机主轴系上的主轴轴承种类多样，且都具有很强的承载能力，包括双列调心滚子轴承、三排柱组合轴承、双列圆锥滚子轴承以及单列圆锥滚子轴承等。
随着风电机组平价时代的到来，在保证质量的前提下，对制造成本提出了越来越高的要求[5]。为了降低风电机组制造成本，随着机组容量的增大，单列圆锥滚子轴承逐渐作为直驱、半直驱和双馈风电机组传动链的主要轴承选型类型。双支撑的单列圆锥滚子轴承，一般采用背对背的安装方式，两轴承具有一定的跨距，可以减少运行过程中两个轴承受载，且增强风机主轴系对风载倾翻力矩的承受能力。相同兆瓦级别的风电机组中，双支撑单列圆锥滚子轴承可以减小轴承尺寸，其中下风向轴承受载较小，可以采用较小的轴承，具有很好的成本优势。
随着国内各风电整机厂技术的进步，关于主轴系以及主轴轴承已经有大量的研究。申屠东华等[6]对大型风电机组传动系统支撑特性进行了分析，详细介绍了单列圆锥滚子轴承支撑轴系的特点。杜静等[7]基于Stribeck计算方法，分析了主轴轴承接触变形，得到了圆锥滚子轴承的接触应力分布。付大鹏等[8]利用Romax软件对风电机组主轴轴承接触应力进行了研究。杨剑飞等[9]通过对双列球面滚子轴承接触应力的求解，分析了主轴轴承载荷、游隙对轴承接触应力的影响。牛宝禛等[10]分析了载荷、转速、润滑脂污染程度对调心滚子轴承疲劳寿命的影响。姜宏伟[11]针对径向游隙对风电调心滚子轴承寿命的影响，得到了轴承最佳的工作游隙。李云峰等[12]针对直驱机组双支撑的单列圆锥滚子轴承，建立了滚动体载荷分布的分析模型，研究了滚动体凸度对轴承接触应力和沟道寿命的影响。董营等[13]对风电圆锥滚子轴承安装工艺进行了研究，保证其合理的安装游隙。肖文等[14]以3 MW机型主轴轴承为对象，分析了游隙变化对双列圆锥滚子轴承承载接触载荷的影响。Zheng等[15]进行了变工况下双列圆锥滚子轴承疲劳寿命研究。章滔等[16]基于非线性弹性接触方程，建立滚子-滚道接触模型，进行了三排圆柱滚子轴承滚子修形方法研究。吕润楠等[17]建立了具有滚道波纹度的双列圆锥滚子轴承动力学计算模型，分析了波纹度波数、幅值对轴承振动特性的影响。采用单列圆锥滚子轴承双支撑的风机主轴系结构，近几年才开始在我国风电行业广泛应用，其游隙的控制至关重要，目前对此结构轴承游隙的研究还相对较少。
文章基于某中速永磁风力发电机组主轴系，开展相关研究。旨在得到不同轴向游隙下，轴承承载区域、轴承滚道寿命、最大接触应力的变化趋势，来确定配对单列圆锥滚子轴承理想轴向工作游隙范围，提高轴承运行的可靠性。
-
单列圆锥滚子轴承具有一定的接触角，可以承受不同方向载荷，具有优秀的承载性能和旋转精度，通常需要配对使用，游隙也需要成对调整。且圆锥滚子轴承对于游隙的要求相当苛刻，游隙调整是否适当，直接关系到轴承最终运行的性能及使用寿命[18]。
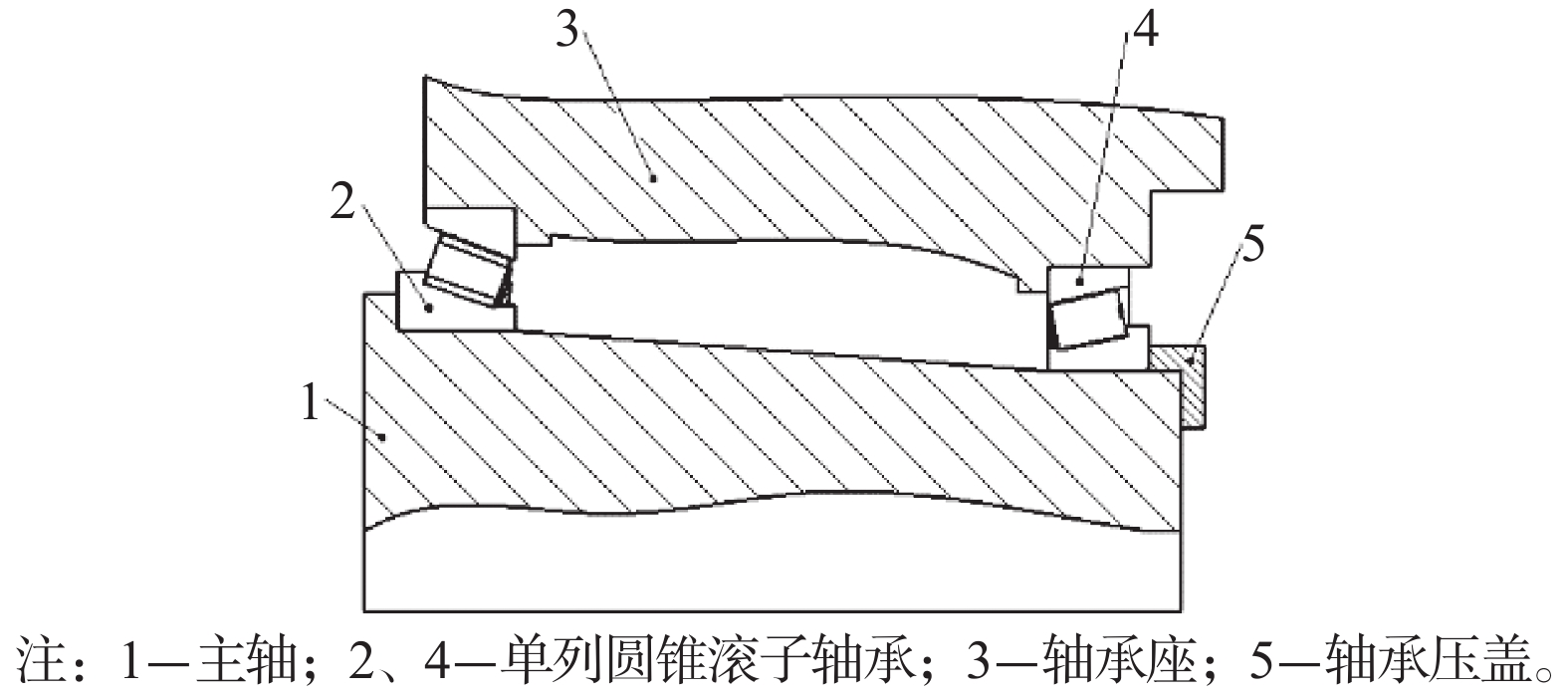
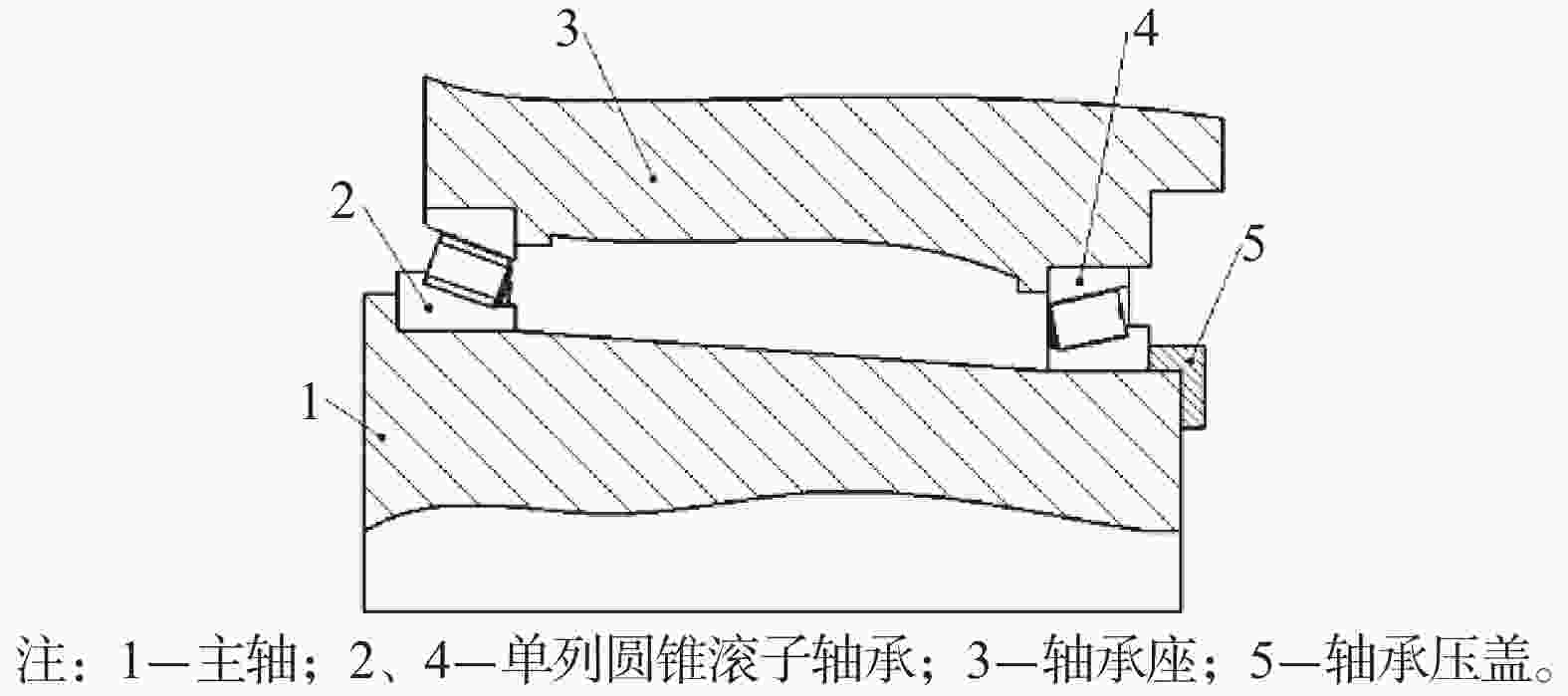
圆锥滚子轴承游隙可以定义为滚动体和滚道之间的轴向间隙，轴向游隙是衡量圆锥滚子轴承的典型游隙，轴向游隙往往决定轴承寿命、噪声及振动等性能[19]。在安装时调整轴向游隙是圆锥滚子轴承的固有优点，对于背对背安装如图1所示，通常用轴承压盖5对轴承内圈轴向位置进行调整，来完成配对轴承装配轴向游隙的调整，保证配对轴承运行时处于理想轴向工作游隙范围内。
Figure 1. Layout diagram of single row tapered roller bearings
由于风力发电机组主轴轴承运行工况低速、重载且复杂多变，为了增加轴承2个有效支撑点的距离，提高系统抗倾翻力矩的能力，单列圆锥滚子轴承采用背靠背装配。适当的预紧有利于提高配对单列圆锥滚子轴承的承载能力[20]，风电主轴系为了提高整个系统的刚性，要求配对轴承运行具有一定的预紧，即要求配对轴承运行时为负游隙。
-
滚动体与沟道接触为有限长线接触，超出了Hertz理论的范畴。有限长接触问题的基本方程为[9]：
$$ \iint_\varOmega {p\left( {x,y} \right)}{\mathrm{d}}x{\mathrm{d}}y = Q $$ (1) $$ \frac{1}{{\text{π} {E'}}}\iint_\varOmega {\frac{{p\left( {{x'},{y'}} \right){\mathrm{d}}{x'}{\mathrm{d}}{y'}}}{{\sqrt {{{\left( {x - {x'}} \right)}^2} + {{\left( {y - {y'}} \right)}^2}} }}} = \delta - z\left( {x,y} \right) $$ (2) 式中：
Ω ——接触区域；
p ——接触应力（MPa）；
Q ——滚动体与沟道的作用力（N）；
$ {E^{'}} $ ——当量弹性模量（MPa）；
$ \delta $ ——滚动体与沟道接触中心弹性趋近量（mm）；
z ——滚动体与沟道接触表面的初始距离（mm）。
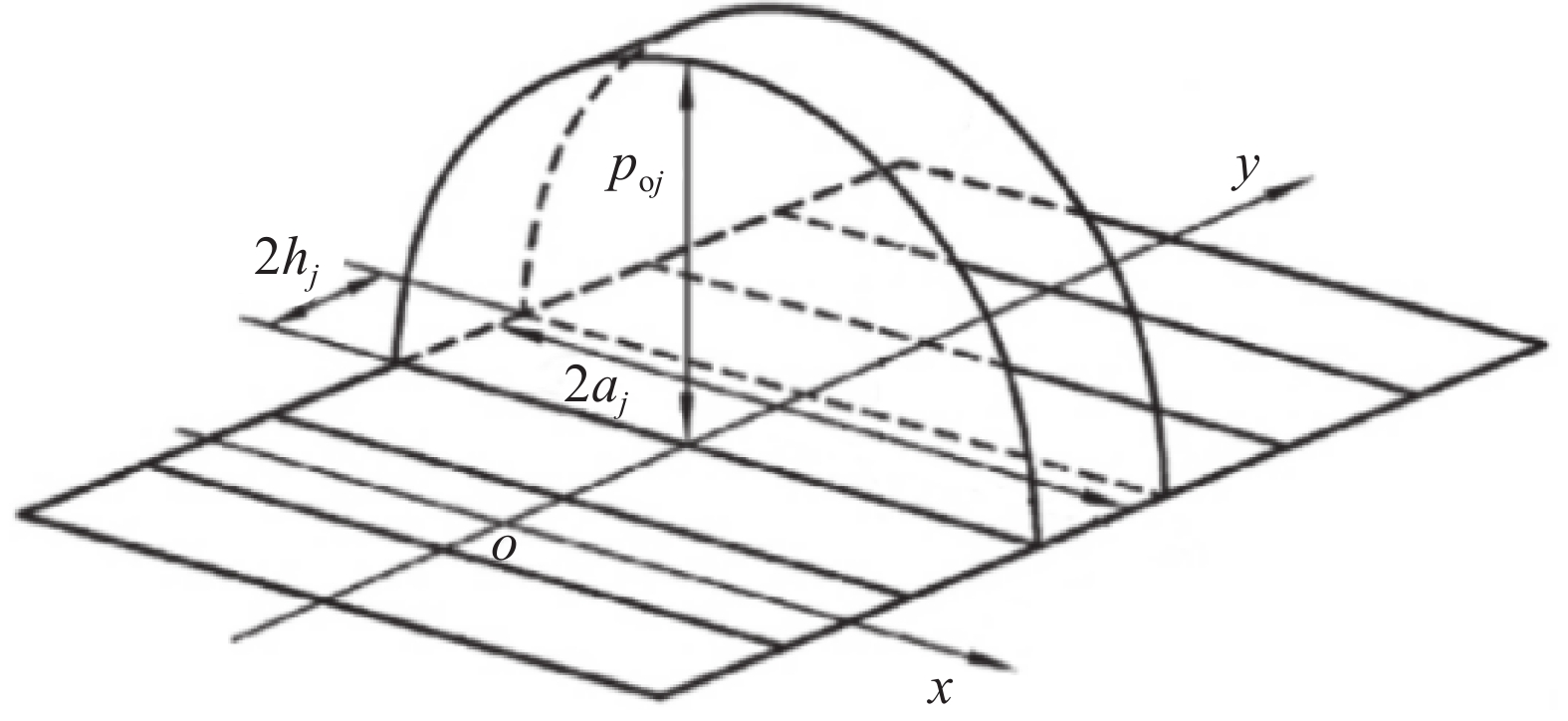
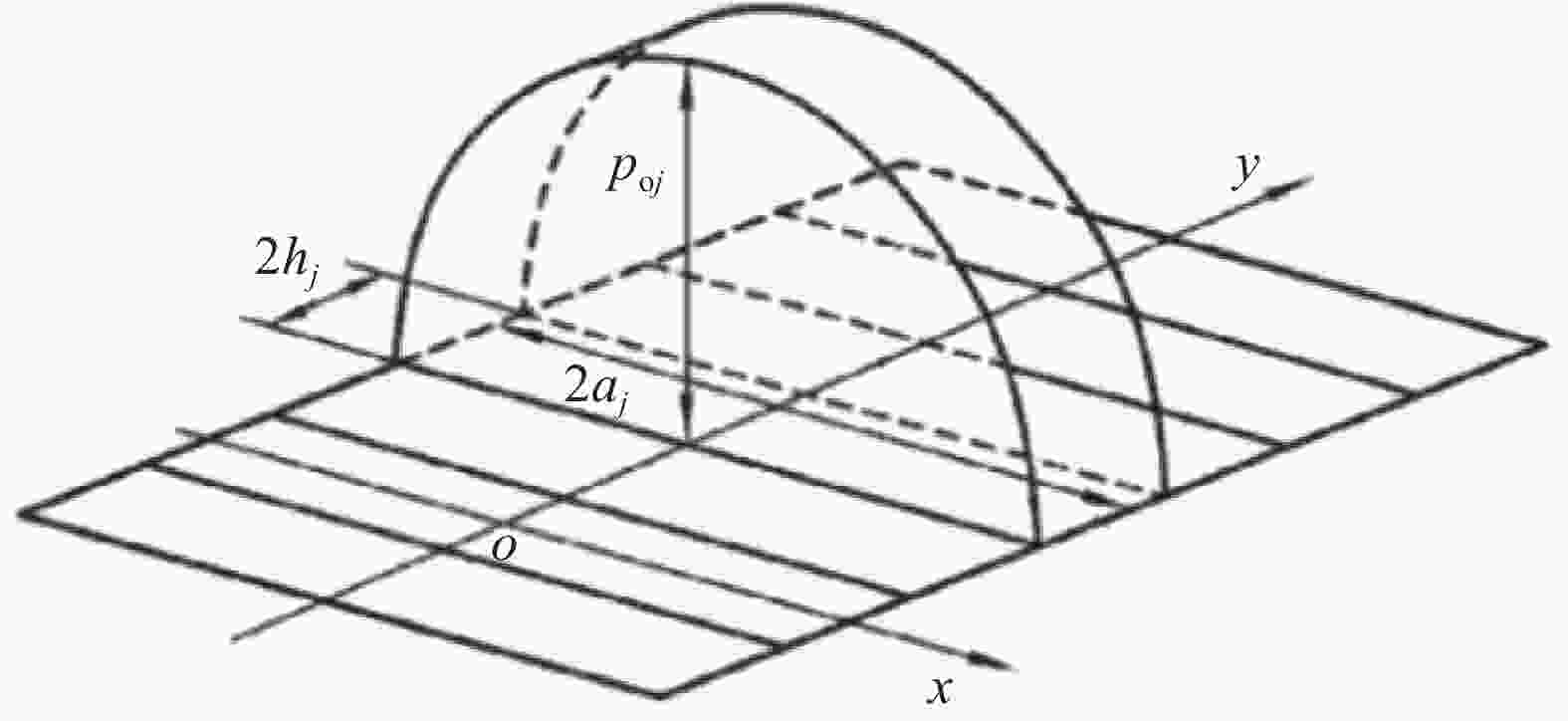
针对滚子与滚道线接触问题，可以采用罗继伟[21]的方法，如图2所示，将接触区域沿滚动体轴向（y轴）分割为n个单元，假定切片区域j内的接触应力pj沿母线方向符合均匀分布，沿x轴为赫兹分布：
Figure 2. Contact area coordinate system
$$ {p_j}\left( {x,y} \right) = {p_{{\mathrm{o}}j}}\sqrt {1 - {{\left( {\frac{x}{{a{}_j}}} \right)}^2}} $$ (3) 式中：
poj ——接触切片j中心处的最大接触应力（MPa）；
2aj、2hj ——接触切片j的长边和短边（mm）。
切片j产生的接触载荷为：
$$ {q_j} = 2{h_j}\int_{ - {a_j}}^{{a_j}} {{p_{{\mathrm{o}}j}}} \sqrt {1 - {{\left( {x/{a_j}} \right)}^2}} {\mathrm{d}}x = \text{π}{a_j}{h_j}{p_{{\mathrm{o}}j}} $$ (4) 柔度系数为：
$$ {D_{ij}} = \int\limits_{ - {a_j}}^{{a_j}} {\int\limits_{{y_j} - {h_j}}^{{y_j} + {h_j}} {\frac{{\sqrt {1 - {{\left( {{x'}/{a_j}} \right)}^2}} }}{{\sqrt {{x'}^2 + {{\left( {{y_i} - {y_j} - {y'}} \right)}^2}} }}} } {\mathrm{d}}{x'}{\mathrm{d}}{y'} $$ (5) 将式（1）、式（2）进行离散化处，可以得到：
$$ Q = \text{π} \sum\limits_{j = 1}^n {a{}_j{h_j}} {p_{{\mathrm{o}}j}} $$ (6) $$ \frac{1}{{\text{π} {E'}}}\sum\limits_{j = 1}^n {{D_{ij}}} {p_{{\mathrm{o}}j}} = \delta - {Z_i}\left( {{y_i}} \right)\;\; \left( {{{i = 1,2,}} \cdots n} \right)$$ (7) 式中：
Zi(yi)——滚动体第i个切片处与沟道表面的初始间距（mm）。
式（6）和式（7）构成了滚子与滚道接触力学模型的方程组，运用数值解法即可得到各切片单元接触应力poj。利用式（3）和式（4）进一步计算得到整个接触区域的应力分布和每个切片的接触载荷。
-
风电主轴承运行工况复杂多变，在进行轴承滚道疲劳寿命计算时，需要考虑润滑、污染、倾斜、轴承工作游隙等因素的影响。所以采用ISO/TS
16281 标准[22]介绍的方法，进行轴承修正参考额定寿命的计算。对应于90%可靠度的基本参考额定寿命为：
$$ {L_{10{\mathrm{r}}}} = {\left\{ {\sum\limits_{k = 1}^{{n_{\mathrm{s}}}} {\left[ {{{\left( {\dfrac{{{q_{{{k}}{\mathrm{ci}}}}}}{{{q_{{{k}}{\mathrm{ei}}}}}}} \right)}^{ - 9/2}} + {{\left( {\dfrac{{{q_{{{k}}{\mathrm{ce}}}}}}{{{q_{{{k}}{\mathrm{ee}}}}}}} \right)}^{ - 9/2}}} \right]} } \right\}^{ - 8/9}} $$ (8) 在基本参考额定寿命的基础上，进行修正得到更符合轴承实际运行的修正参考额定寿命：
$$ \begin{split} &{L_{n{\mathrm{mr}}}} = \\&{a_1}{\left( {\sum\limits_{k = 1}^{{n_{\mathrm{s}}}} {\left\{ {{{\left[ {{a_{{\mathrm{ISO}}}}\left( {\frac{{{e_{\mathrm{C}}}{C_{{\mathrm{ur}}}}}}{{{P_{k{\mathrm{s}}}}}},\kappa } \right)} \right]}^{ - 9/8}}\left[ {{{\left( {\frac{{{q_{k{\mathrm{ci}}}}}}{{{q_{k{\mathrm{ei}}}}}}} \right)}^{ - 9/2}} + {{\left( {\frac{{{q_{k{\mathrm{ce}}}}}}{{{q_{k{\mathrm{ee}}}}}}} \right)}^{ - 9/2}}} \right]} \right\}} } \right)^{ - 8/9}} \end{split} $$ (9) 式中：
$ {a}_{1} $ ——可靠度修正系数；
$ {a}_{\mathrm{I}\mathrm{S}\mathrm{O}} $ ——修正系数；
$ {e}_{\mathrm{C}} $ ——污染系数；
$ {C}_{\mathrm{u}\mathrm{r}} $ ——径向载荷疲劳极限（N）；
$ \kappa $ ——润滑剂黏度比；
$ {P}_{{k}\mathrm{s}} $ ——轴承第k个切片的当量动载荷（N）；
$ {q}_{{k}\mathrm{c}\mathrm{i}} $、$ {q}_{{k}\mathrm{c}\mathrm{e}} $——内圈和外圈某一轴承切片处的基本额定动载荷（N）；
$ {q}_{{k}\mathrm{e}\mathrm{i}} $、$ {q}_{{k}\mathrm{e}\mathrm{e}} $——内圈和外圈某一切片处的当量动载荷（N）。
对于多工况载荷谱，可以分别计算每个工况下的轴承滚道寿命，在运用GL规范介绍方法计算合并修正参考额定寿命为：
$$ {L_{10{\mathrm{mr}}}} = \dfrac{{\displaystyle \sum {{q_i}} }}{{\displaystyle \sum {\dfrac{{{q_i}}}{{{L_{10{\mathrm{mr}}i}}}}} }} $$ (10) 式中：
qi ——第i个载荷等级的分时（h）；
L10mri ——第i个载荷等级的轴承修正参考额定寿命（h）。
-
本文利用精益传动设计软件，进行建模和分析计算。精益传动设计软件可以进行传动系统二维和三维建模，能涵盖整个传动产品设计流程。吸收了国际设计标准规范，不仅可以实现齿轮、轴承、轴等传动部件的分析计算，还可以进行系统NVH、变形、模态以及转子动力学等关键技术的动力学分析计算。支持多任务、多数据快速并行算法，是一款多物理场耦合的大型传动系统设计分析软件。主要面向汽车、风电、船舶、燃机等行业的国产传动系统仿真计算工业软件。
-
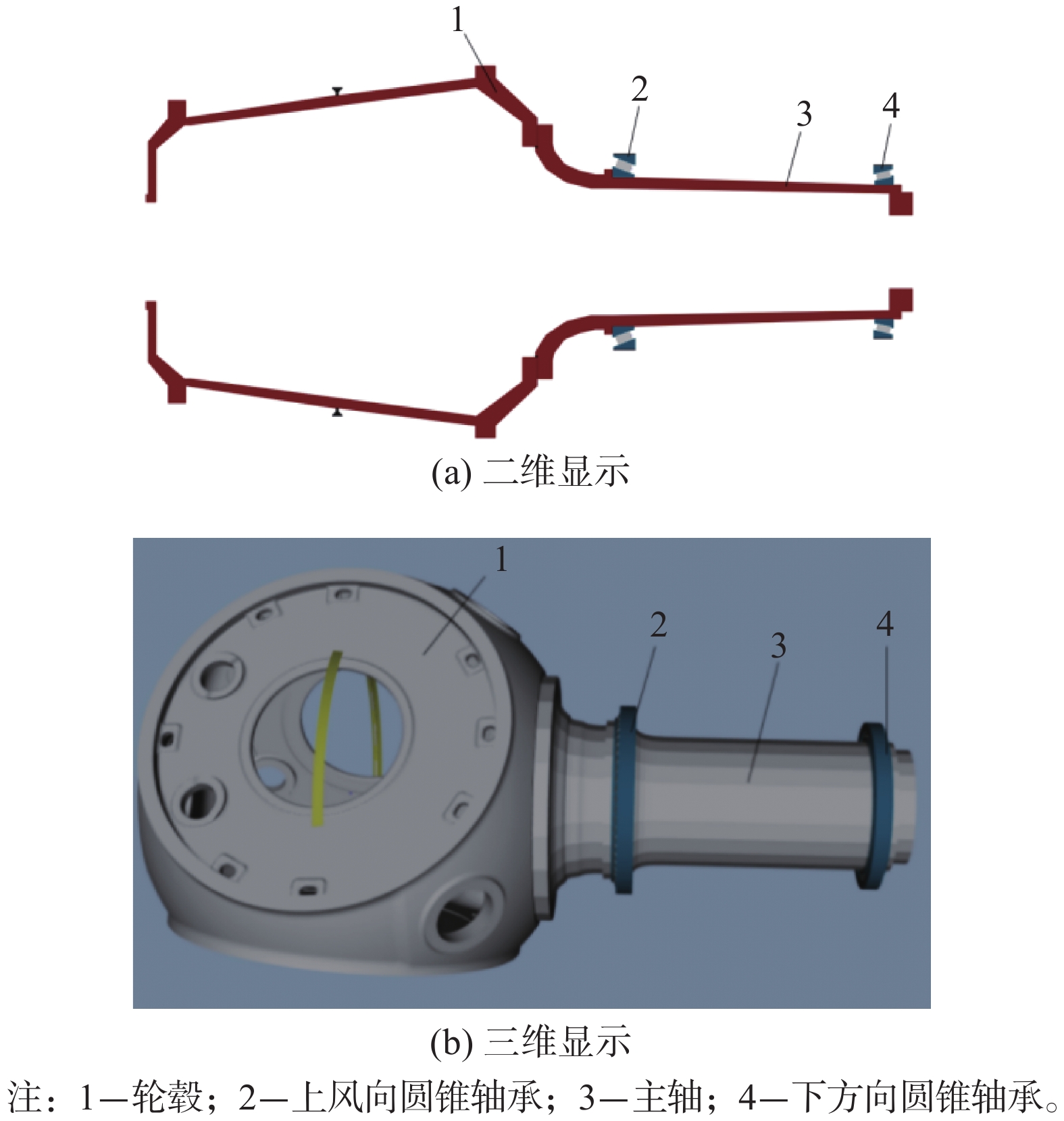
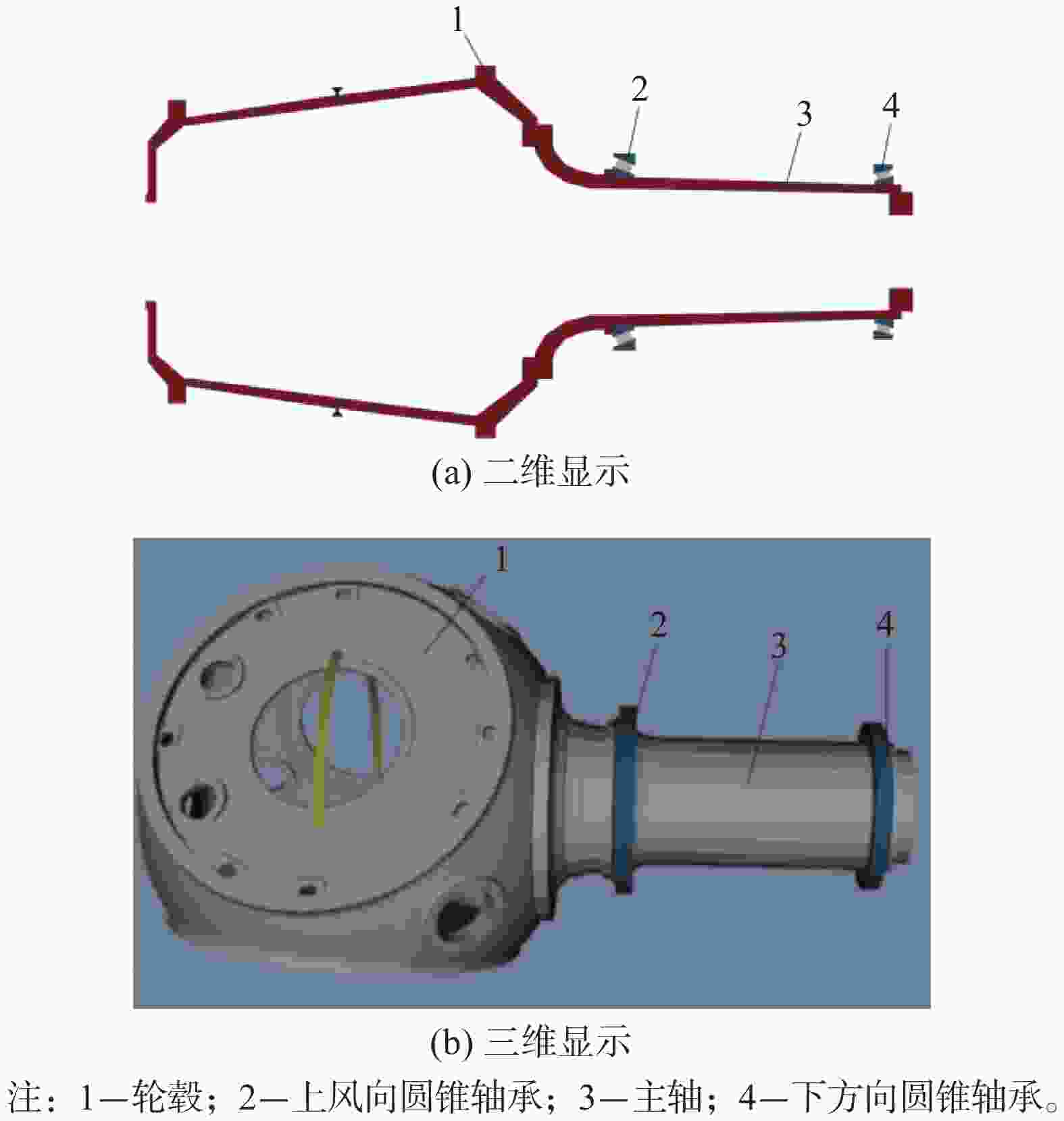
以某风电机组主轴系为例，利用精益传动设计软件，建立了轮毂、主轴、上风向轴承和下风向轴承一体化的分析模型，如图3所示。
Figure 3. Simulation analysis model
其中轮毂和主轴设置好材料属性柔性化处理后导入精益传动设计软件，上下风向轴承可以根据轴承参数在软件中自定义设定添加，材料属性和轴承参数分别如表1和表2所示。轮毂中心施加风机叶轮中心载荷，软件中设置上下风向单列圆锥滚子轴承总轴向游隙，进行仿真分析。
名称 弹性模量/GPa 泊松比 密度/(kg·m−3) 主轴 200 0.30 7 850 轮毂 169 0.28 7 300 Table 1. Material properties
参数 上风向轴承 下风向轴承 内径/mm 1 500 1 350 外径/mm 1 965 1 740 宽度/mm 220 190 重量/kg 1 751 1 153 Table 2. Bearing parameters
-
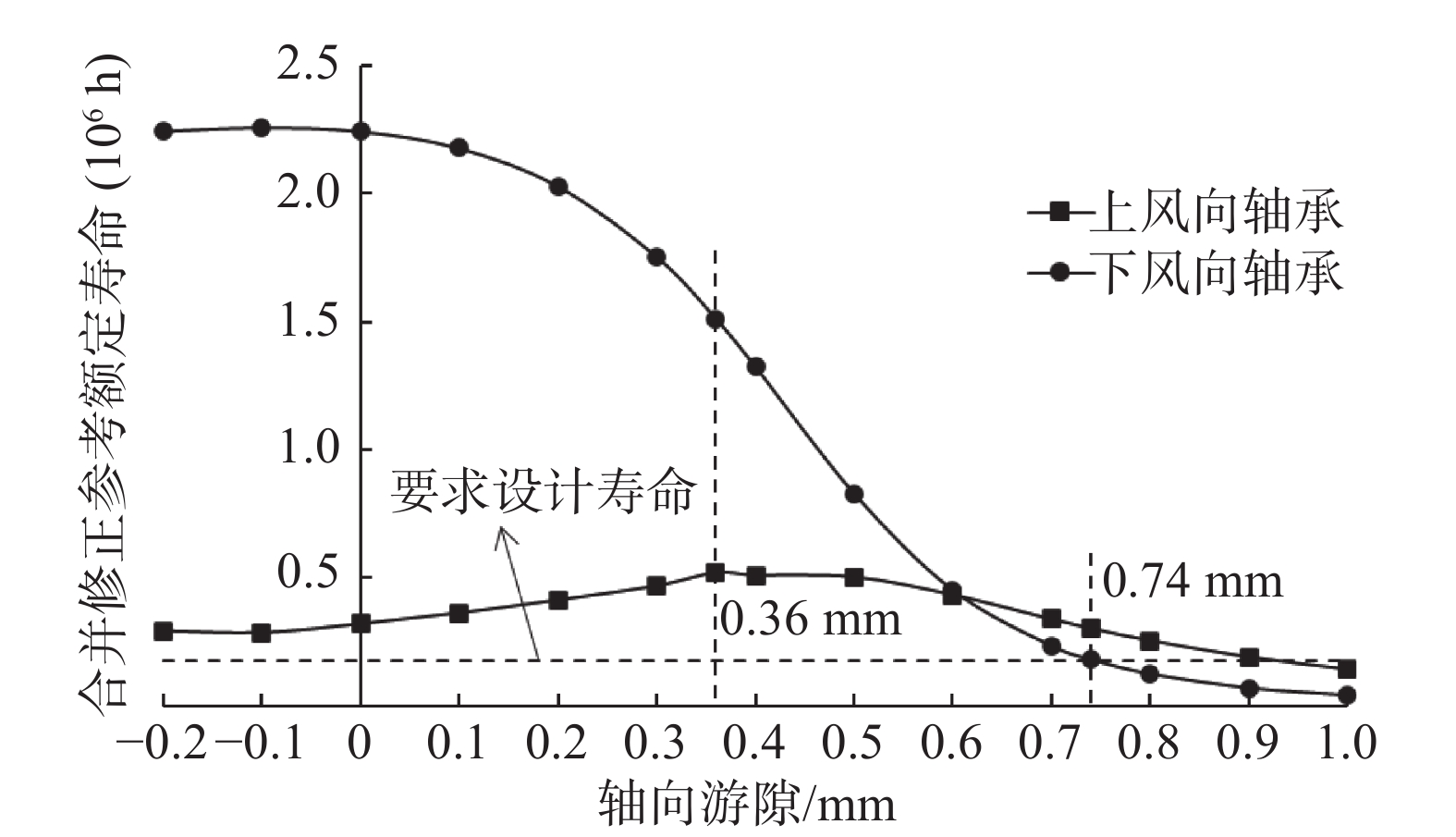
主轴转速为8.8 r/min，采用油润滑，运动粘度为320 mm2/s，应用环境为正常清洁度。通过分析模型的计算，得到了不同轴向游隙下，上下风向轴承的合并修正参考额定寿命、承载区域以及最大接触应力的变化趋势。图4~图6横坐标负数为正游隙，表示轴承间隙；正数为负游隙，表示轴承预紧。
Figure 4. Relationship between clearance and bearing life
Figure 5. Relationship between clearance and load area
Figure 6. Relationship between clearance and maximum contact stress
风电机组疲劳载荷分析形式主要有3种：实时的时间序列、载荷持续分布（LDD）和等效疲劳载荷[23]。主轴轴承滚道疲劳寿命一般采用载荷持续分布进行计算[24]，载荷包含力矩和力在各方向上的分量，即Mx，My，Mz，Fx，Fy，Fz，以及时间和转速。
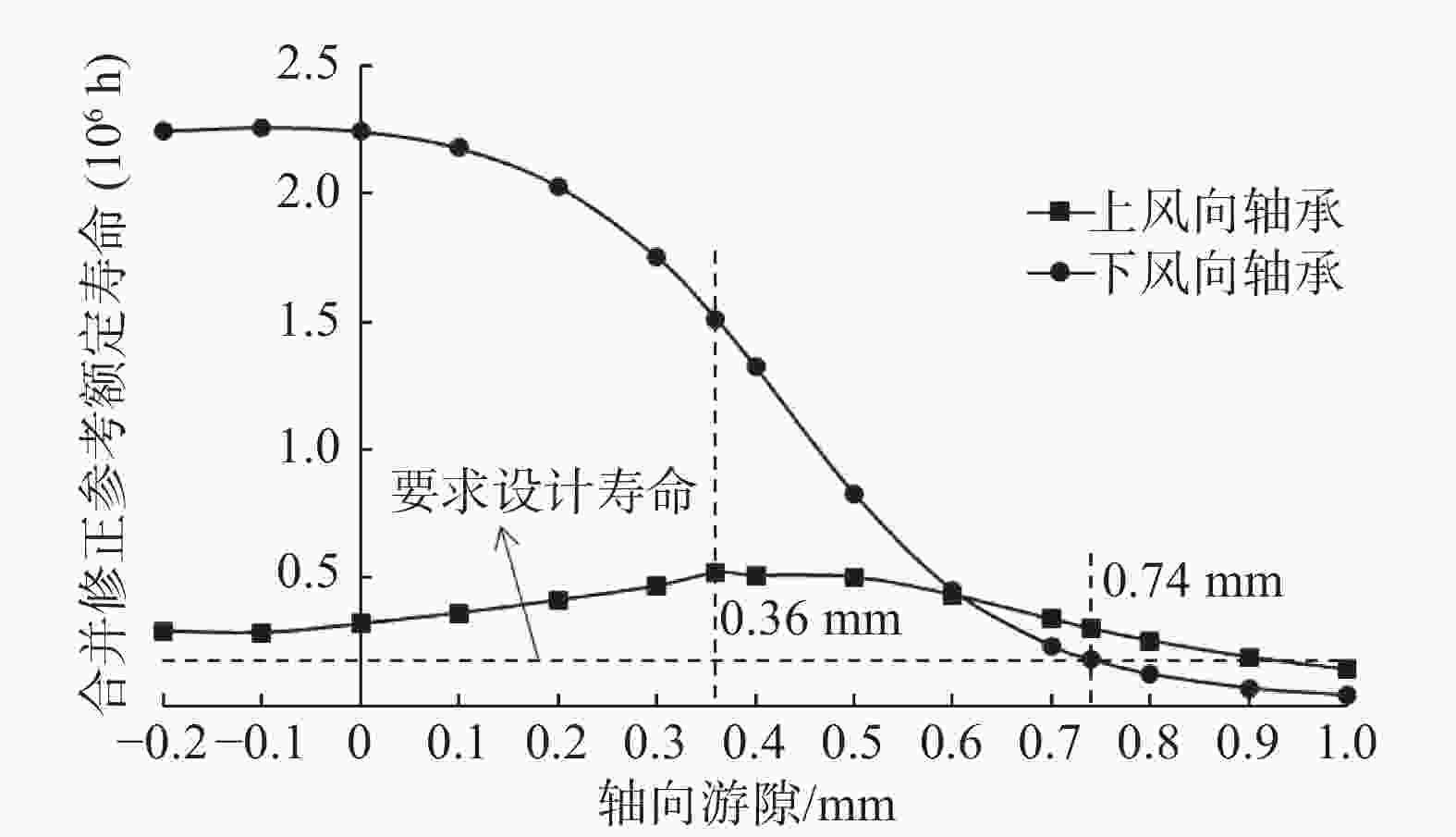
图4为在轮毂中心LDD疲劳载荷下，不同轴向游隙下，轴承滚道合并修正参考额定寿命的变化趋势。随着轴向游隙的减小，上风向轴承滚道寿命先增加后减小，下风向轴承滚道寿命逐渐减小；当轴向游隙为−0.6 mm，上风向轴承和下风向轴承滚道寿命接近；当轴向游隙值小于−0.74 mm时，下风向轴承滚道寿命低于要求设计寿命7 300 d；当轴向游隙为−0.36 mm时，上风向轴承滚道寿命达到最大。因此，上风向轴承和下风向轴承同时满足大于要求设计寿命和轴向工作游隙为负游隙的条件下，合适轴向工作游隙范围为−0.74 mm~0，配对轴承寿命最优轴向工作游隙为−0.36 mm。
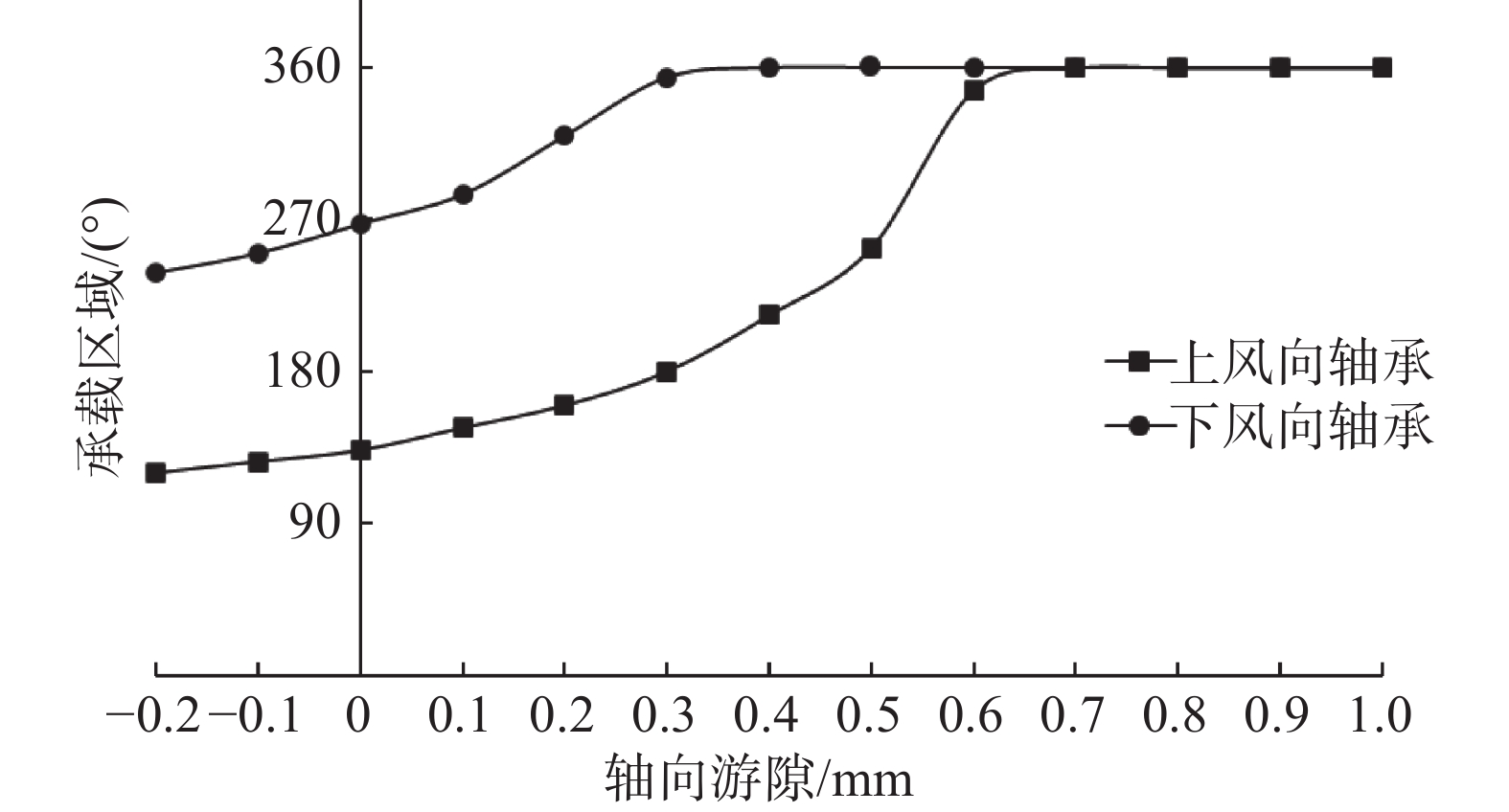
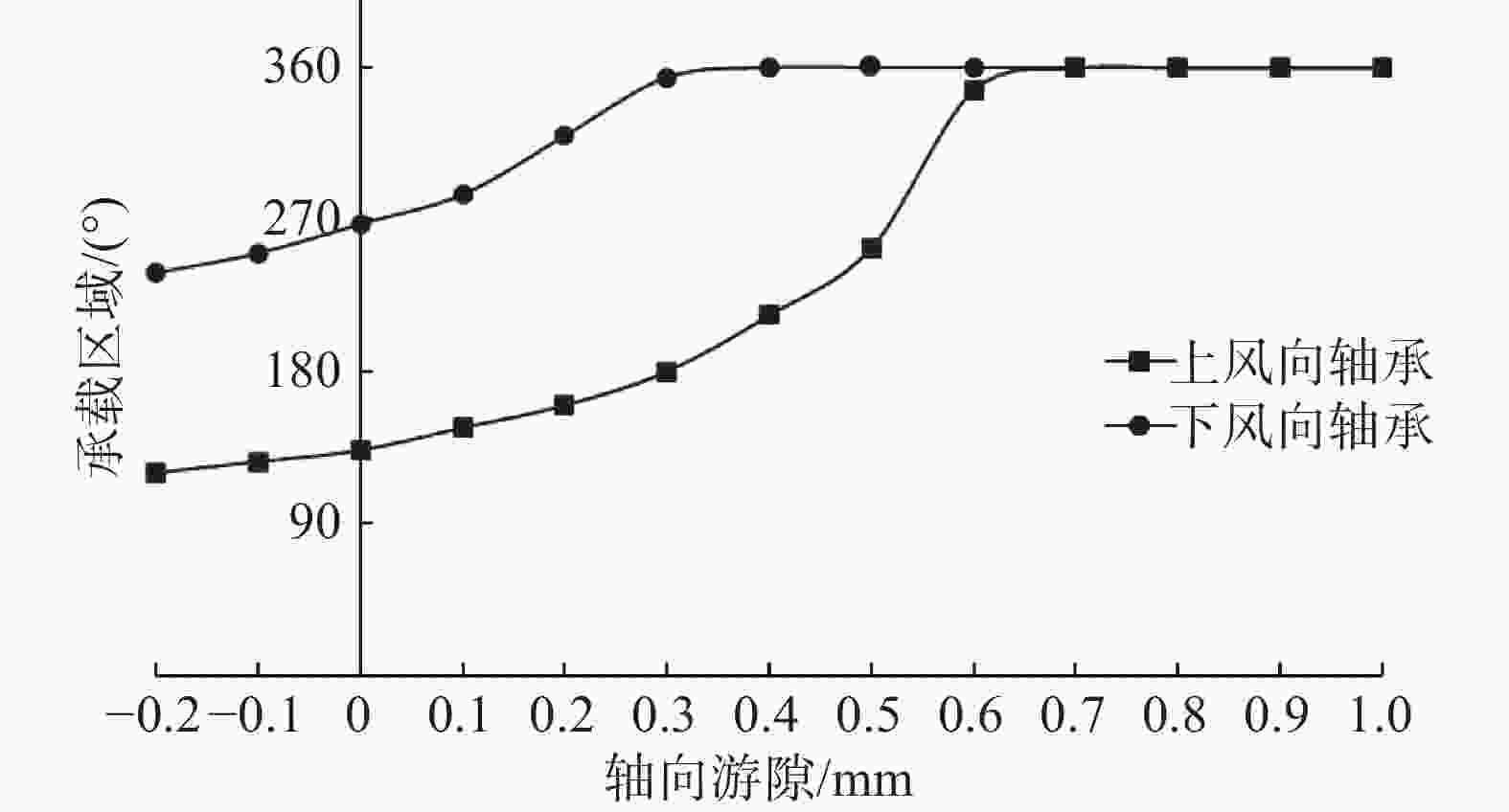
图5为不同轴向游隙下，上风向轴承和下风向轴承承载区的变化。由图可知，随着轴向游隙的减小，上风向轴承和下风向轴承承载区逐渐增大。下风向轴承承载区始终大于180°，有超过一半滚子个数在承载区内。轴向游隙大于−0.3 mm时，上风向轴承承载区小于180°，小于一半滚子个数位于承载区。
为了减少单个滚子的接触应力，风电轴承往往要求至少有一半的滚子位于承载区。上风向轴承和下风向轴承同时满足至少有一半滚子位于承载区的轴向工作游隙范围是−1~−0.3 mm。
综上所述，同时考虑轴向游隙与寿命、承载区的关系，可以得到配对的上风向轴承和下风向轴承理想的轴向工作游隙范围为−0.74~−0.3 mm。
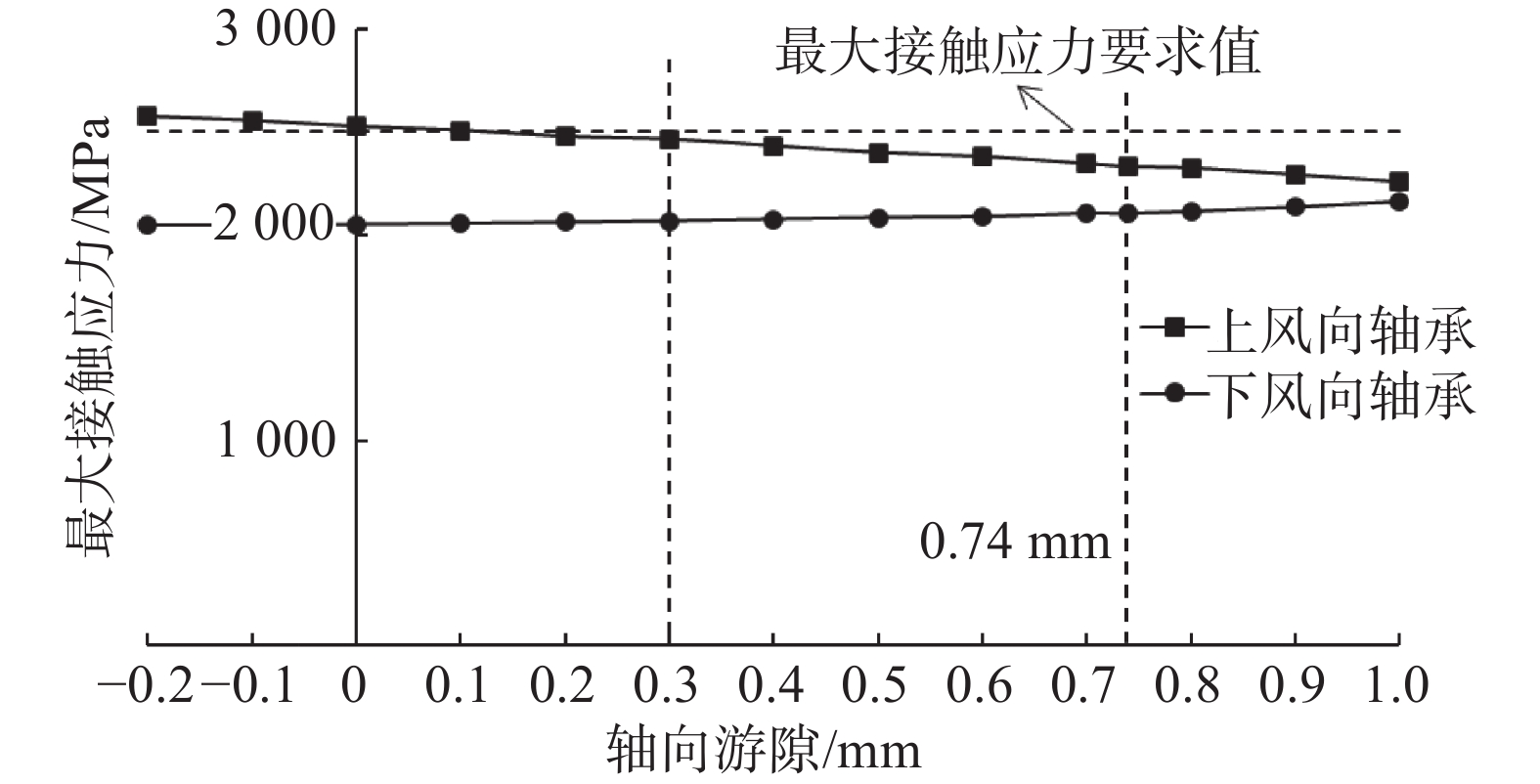
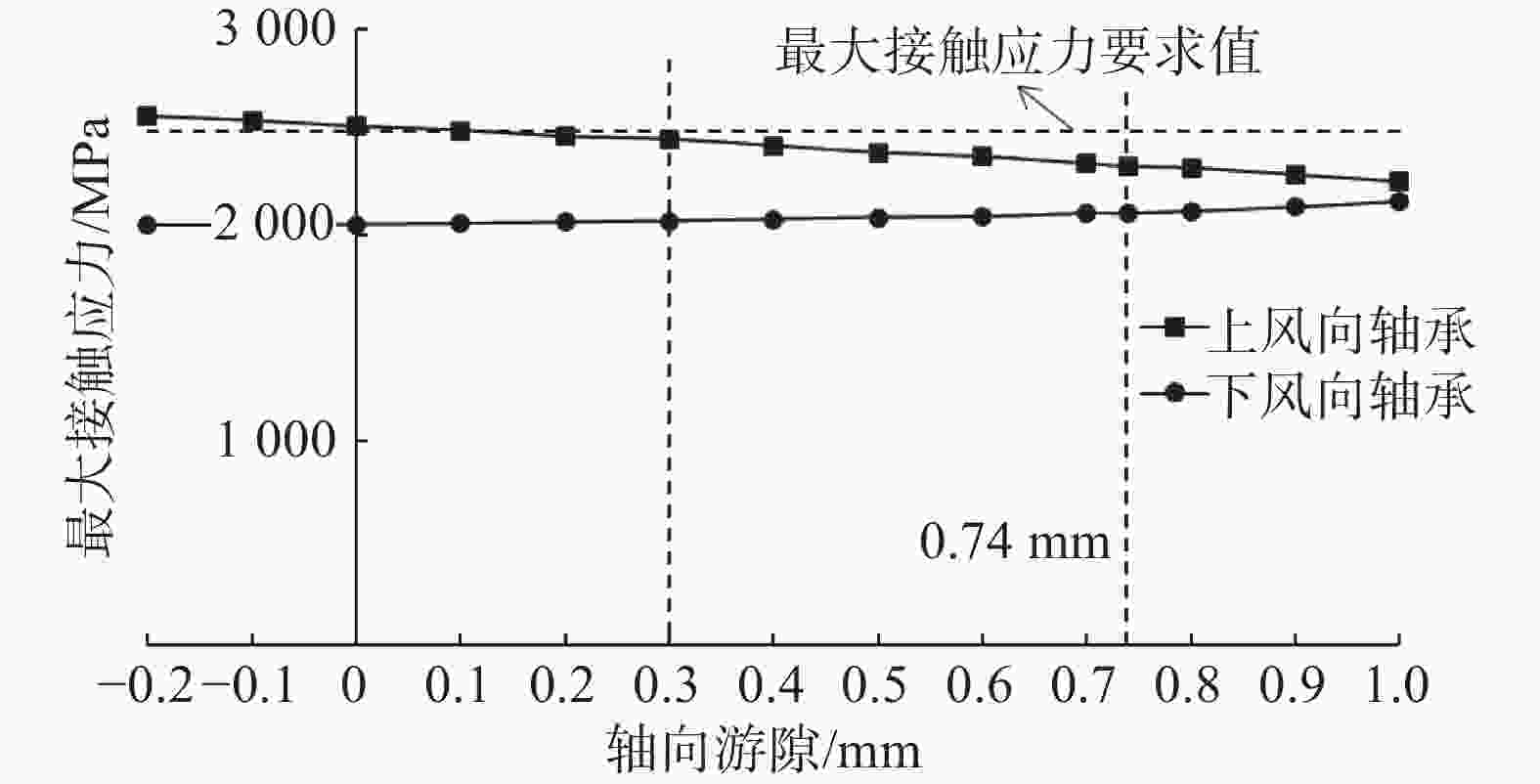
图6为轮毂中心极限载荷下，不同轴向游隙下，上风向轴承和下风向轴承最大接触应力变化。由图可知，随着轴向游隙减小，上风向轴承最大接触应力逐渐减小，下风向轴承最大接触应力逐渐增大；轴向工作游隙−0.74~−0.3 mm范围内，上下风向轴承最大接触应力均小于最大接触应力要求值2 500 MPa。因此，上述轴向工作游隙范围内，上下风向轴承满足极限的设计要求，进一步证明上述轴向工作游隙是合理的。
-
以某中速永磁风力发电机组为例，基于传动系统动力学软件，通过建立轮毂、主轴、上风向轴承和下风向轴承一体化的动力学分析模型，研究了不同轴向游隙下，上下风向轴承滚道寿命、承载区域、接触应力的变化趋势，最终研究得到了该风电机组主轴配对单列圆锥滚子轴承的理想轴向工作游隙范围为−0.74 ~−0.3 mm，并在该游隙范围内，上下风向轴承最大接触应力均小于要求值2 500 MPa。研究结论对轴承和主轴系的可靠运行具有重大意义，为主轴轴承的工作游隙研究确认提供了方法和参考。
Analysis on Operating Clearance of Matched Single Row Tapered Roller Bearings for Wind Turbine Main Shaft
doi: 10.16516/j.ceec.2024.5.12
- Received Date: 2023-05-19
- Rev Recd Date: 2023-07-28
- Available Online: 2024-09-30
- Publish Date: 2024-09-10
-
Key words:
- single row tapered roller bearings /
- axial operating clearance /
- raceway life /
- contact stress
Abstract:
| Citation: | BU Zhongjie, ZHANG Tao, HE Luzhong, et al. Analysis on operating clearance of matched single row tapered roller bearings for wind turbine main shaft [J]. Southern energy construction, 2024, 11(5): 116-122 doi: 10.16516/j.ceec.2024.5.12
|
DownLoad:
