-
低碳能源指能够排放少量或不排放二氧化碳为主的温室气体的能源[1]，如核能和部分可再生能源。随着“双碳”战略实施，我国朝着能源低碳化发展，推进能源转型，对能源效率进行提升，并降低碳排放量。
评价理论可把握系统性能与运行水平[2]。国内外许多学者对低碳经济以及能源综合评价进行研究。赵振宇等[3]基于粗糙集理论筛选指标分析新能源城市发展。许龙等[4]提出可再生能源资源禀赋综合评价指标体系并采用层次分析-熵权-TOPSIS(Technique for Order Preference by Similarity to Ideal Solution)组合法对多能互补系统进行评价。谭伟等[5]对智能电网低碳指标体系进行讨论并提出低碳评价指标。还有一些学者[6-8]从技术、经济、环境和社会等多个方面构建综合评价体系，分析热电联产系统性能和低碳环境等对象。这些评价指标主要关注经济和系统整体性能，缺乏对能源低碳利用针对性评价体系。在推动碳减排工作进程的过程中，需要通过构建低碳利用评价指标体系来把握能源低碳发展方向，更科学客观地了解能源低碳利用的情况。为此，本文章将对目前国内外能源低碳利用评价对象和评价指标进行梳理归纳，建立低碳利用评价指标体系，并对评价模型与方法进行综述。最后对能源低碳利用评价研究进行总结与展望。
-
能源低碳利用评价可分为2种：（1）对具体能源系统进行技术上评价，比如对微能源网、冷热电联供等能源系统进行能效、经济、技术等方面评价；（2）对某个区域能源现状进行评价，多考虑电能占终端能源消费比重、单位GDP的CO2排放等宏观指标。
-
针对能源系统的评价研究中，多能互补能源系统、能源互联网的研究较为丰富。能源系统评价对象和方法如表1所示。从表中可以看出，能源系统评价研究的对象为现有的园区综合能源系统或研究算例中构造的微能源网。
文献 研究对象 评价方法 [9] 企业综合能源系统 使用层次分析法和模糊综合评价理论进行综合评价。 [10] 深圳某园区综合能源系统 考虑绿色低碳因素，采用层次分析法进行评价。 [11] 广州某工业园区综合能源项目 考虑技术与效益两大类指标，顶层指标与中层指标通过下一层的评分与权重分层获得评分。 [12] 园区综合能源系统项目 对定量指标进行计算，对定性指标进行专家评分与模糊处理，通过模糊综合评价方法进行分析。 [13] 我国东南部某工业园区 提出“基于权重向量偏差最小”组合赋权法，综合主观客观赋权方法进行电能替代效果评价。 [14] 多能互补系统 基于矩阵评估理论算法，集成主客观赋权方法进行电能替代综合效益评价。 [15] 北京市某医院综合能源项目 结合层次分析法和熵权法得到组合权重通过灰色关联分析法得到评价结果。 [16] 综合能源系统 通过熵权-TOPSIS法对建立综合能源系统进行评价。 [17] 微能源网 考虑一次能源消耗、投资成本、二氧化碳排放量和供能可靠性构建评价指标并用于对含冷热电联产系统的微能源网进行优化。 Table 1. Energy system assessment
在针对能源系统的评价中，评价对象为工程项目或根据具体情况所配置的能源系统。评价指标多涉及系统技术指标、能源利用效率、环境影响、经济效益等方面。目的为对多模式运行的能源系统进行分析，评估出最优运行模式，或对能源系统经济效益或技术性指标进行评估优势与不足，提供优化方向。
-
针对区域能源评价中，通常针对宏观指标进行考察，从区域能源高质量发展、区域能源绿色发展、区域能源安全等方面进行评价，强调区域总体发展水平。区域能源评价对象和方法如表2所示。从表中可看出，区域能源评价研究的研究对象多为长三角京津冀等区域、中国某省或市的能源发展情况。
文献 研究对象 评价方法 [18] 重庆市 选用DEA(Data envelopment analysis)模型对重庆市能源效率进行评价。 [19] 河南省 针对区域能源绿色发展水平，运用熵值法进行评价。 [20] 中国 筛选得到15个相互关联性弱的评价指标，采用时序加权平均算子得到能源发展质量动态指数。 [21] 中国 构建低碳指标评价体系，使用熵权-TOPSIS分析法进行评价。 [22] 沈阳市 通过工业低碳利用指标体系结合层次分析法进行评价。 [23] 西部地区 构建区域可再生能源发电绩效指标运用DEA模型进行评价。 [24] 中国八大经济区 对八大经济区可持续发展水平进行测度，用TOBIT模型回归识别影响因素。 [25] 长三角地区 构建有内在联系的能源-经济-环境系统评价指标体系，采用层次分析法进行评价。 [26]
[27]京津冀地区、福建省 通过熵权法评价地区能源-经济-环境系统发展水平。 [28]
[29]北京市 使用熵权法与正负理想解逼近TOPSIS法进行评价。 Table 2. Regional energy assessment
在针对区域性能源低碳利用评价中，评价对象为区域性能源发展水平。评价指标主要为绿色低碳程度、能源转型、能源结构、能源综合利用效率等宏观指标。目的为对区域性能源生产与消耗进行低碳利用水平评价，考察出得分较低的指标，用于优化与规划，引导区域性能源朝着绿色低碳高效方向发展。
-
本文将从能源低碳指标、能源利用指标和能源安全指标3个维度，对能源低碳利用评价指标研究现状进行梳理。
评价指标中的统计数据来源主要分为2类：（1）能源系统评价；（2）对区域能源评价。前者通常是在研究算例中得到相关数据，如新能源功率、负荷功率和系统碳排放量等；后者通常在相关统计年鉴、统计公报中获得相关数据。污染物排放量的数据一般通过排放因子进行计算[30-31]。
-
能源低碳指标主要表征研究对象对环境友好程度、对外界环境碳排放与污染物排放程度、对内部低碳能源利用程度。
1)二氧化碳排放量
一次能源消耗过程中二氧化碳总排放量常用计算式（1）为：
$$ {B_1} = a \times {Q_2} + b \times {Q_3} $$ (1) 式中：
$ a $ ——燃煤发电的二氧化碳排放因子(g/kWh)；
$ b $ ——天然气燃烧的二氧化碳排放因子(g/Nm3)；
$ {Q_2} $——燃煤电厂发电量(kWh)；
$ {Q_3} $——燃气机消耗天然气总量(Nm3)。
在区域能源评价中碳排放量普遍采用碳排放系数法[32]，计算式（2）为：
$$ {C_{{\text{C}}{{\text{O}}_{\text{2}}}}} = \frac{{44}}{{12}} \times \sum\limits_{n = 1}^8 {{E_n} \times {e_n} \times {O_n}} $$ (2) 式中：
$ {e_n} $ ——第$ n $种化石能源碳排放系数；
$ {O_n} $ ——第$ n $种能源碳氧化率；
$ {C_{{\text{C}}{{\text{O}}_{\text{2}}}}} $——区域碳排放总量（104 t）；
$ {E_n} $ ——区域第$ n $种化石能源消费量（标准煤）。
2)可再生能源替代率
可再生能源替代率指用可再生能源替代化石燃料提供电能比例。可再生能源装机占比计算式（3）为：
$$ {R_{{\mathrm{re}}}} = \frac{{\displaystyle \sum\limits_r {{W_{{\text{RERR}}}}} }}{{{W_{{\text{all}}}}}} \times 100\% $$ (3) 式中：
$ {R_{{\mathrm{re}}}} $ ——可再生能源替代率；
$ {W_{{\text{RERR}}}} $——可再生能源装机容量(kW)；
$ {W_{{\mathrm{all}}}} $ ——总装机容量(kW)。
3)可再生能源利用率
指需求侧中可再生能源利用量所占能源消耗总量比重[33]，表征研究对象消耗能源过程中对可再生能源利用程度，该指标常用于绿色城市评价、区域能源规划研究[34]。可再生能源利用率计算式（4）为：
$$ {R_{{\text{sum}}}} = \frac{{\displaystyle \sum\limits_r {{W_{{\text{REUR}},r}}} }}{{{E_{{\text{sum}}}}}} \times 100\% $$ (4) 式中：
$ {R_{{\text{sum}}}} $ ——可再生能源产能占比；
$ {W_{{\text{REUR}},r}} $——第$ r $种可再生能源转化成可利用能源形式能量的标准煤当量折算值；
$ {E_{{\text{sum}}}} $ ——能源消耗总量的标准煤当量折算值。
4)可再生能源渗透率
因能源最终作用于终端用户，通常对可再生能源渗透率不考虑每个能量开发利用环节，而主要以终端用户所得能量定义可再生能源渗透率[35]，表示为式（5）：
$$ {\lambda _{{\text{re}}}} = \frac{{\displaystyle \sum\limits_r {{R_{{\text{end}},r}}} }}{{\displaystyle \sum\limits_{{r}} {{R_{{\text{end}},r}} + \displaystyle \sum\limits_u {{U_{{\text{end}},u}}} } }} $$ (5) 式中：
$ {\lambda _{{\text{re}}}} $ ——可再生能源渗透率；
$ {R_{{\text{end}},r}} $ ——第$ r $种可再生能源最终被终端用户利用的能量(kWh)；
$ {U_{{\text{end}},u}} $ ——终端用户所得第$ u $种非可再生能源能量(kWh)。
5)人均二氧化碳排放量
人均碳排放量作为一个重要的低碳指标，用于表征区域内人均所产生碳排放量[36]，计算式（6）为：
$$ {\lambda _{{\text{CP}}}} = \frac{{{C_{{\text{C}}{{\text{O}}_{\text{2}}}}}}}{{{E_{{\text{TP}}}}}} $$ (6) 式中：
$ {\lambda _{{\text{CP}}}} $ ——人均二氧化碳排放量(t/人)；
$ {C_{{\text{C}}{{\text{O}}_{\text{2}}}}} $ ——二氧化碳排放总量(t)；
$ {E_{{\text{TP}}}} $ ——总人口数。
6)减排率
减排率用于表征有效节约能量，在能源系统研究里常指二氧化碳减排量程度，计算式（7）为：
$$ {\lambda _{{\text{RR}}}} = \frac{{\Delta E}}{{{E_{{\text{ml}}}}}} \times 100\% $$ (7) 式中：
$ {\lambda _{{\text{RR}}}} $ ——减排率；
$ \Delta E $ ——研究对象能源系统相比常规能源系统在输出相同冷热电量所产生二氧化碳减排量(t)；
$ {E_{{\text{ml}}}} $ ——常规系统二氧化碳理论排放量(t)。
-
能源利用指标主要表征研究对象对能源利用效率、通过消耗能源对经济效益带来的影响、节能减排效率等。
1)一次能源综合利用率
一次能源利用率指能源输出总量与一次能源消耗总量之比[37-38]。该指标通常运用于提供“冷-热-电”能源系统评价，计算式（8）为：
$$ {P_{{\text{PEU}}}} = \frac{{{Q_{\text{e}}} + {Q_{\text{c}}} + {Q_{\text{h}}}}}{{{Q_{\text{1}}}}} \times 100\% $$ (8) 式中：
$ {P_{{\text{PEU}}}} $ ——一次能源综合利用率；
$ {Q_{\text{1}}} $ ——一次能源消耗量(kWh)；
$ {Q_{\text{e}}} $ ——供电量(kWh)；
$ {Q_{\text{c}}} $ ——供冷量(kWh)；
$ {Q_{\text{h}}} $ ——供热量(kWh)。
2)节能率
能源节能率[39]用于表征能源系统对标准煤消耗的节约程度，计算式（9）为：
$$ \lambda _{{\text{save}}}^{} = \frac{{Q_{{\text{ref}}}^{} - Q_{{\text{exa}}}^{}}}{{Q_{{\text{ref}}}^{}}} \times 100\% $$ (9) 式中：
$ {Q_{{\text{ref}}}} $ ——常规系统一次能源消耗量(标准煤);
$ {Q_{{\text{exa}}}} $ ——研究对象系统一次能源消耗量(标准煤)；
$ {\lambda _{{\text{save}}}} $ ——研究对象系统节能率。
3) 单位碳排放能源消费量
单位碳排放能源消费量表征单位能源消费量的碳排放量，可表示为式（10）：
$$ {\lambda _{{\text{CI}}}} = \frac{{{C_{{\text{C}}{{\text{O}}_{\text{2}}}}}}}{{{E_{{\text{sum}}}}}} $$ (10) 式中：
$ {\lambda _{{\text{CI}}}} $ ——单位碳排放能源消费量；
$ {C_{{\text{C}}{{\text{O}}_{\text{2}}}}} $ ——二氧化碳排放总量(t)；
$ {E_{{\text{sum}}}} $ ——能源消耗总量(t/标准煤)。
4) 碳强度
碳强度为单位GDP的二氧化碳排放量[40]，其计算式（11）为：
$$ \lambda _{{\text{EI}}}^{} = \frac{{{C_{{\text{GDP}}}}}}{{{C_{{\text{C}}{{\text{O}}_{\text{2}}}}}}} \times 100\% $$ (11) 式中：
$ {\lambda _{{\text{EI}}}} $ ——碳强度；
$ {C_{{\text{C}}{{\text{O}}_{\text{2}}}}} $ ——二氧化碳排放量(t)；
$ {C_{{\text{GDP}}}} $ ——区域GDP总额(元)。
-
能源安全指标主要表征研究对象对外能源依赖程度或供能的可靠性。
1)能源缺供总量
系统供能缺额定义为能源缺供总量，该指标越小则可靠性越高，该供能指提供冷能、热能、电能等[11]，表示为计算式（12）：
$$ {\mathrm{EN}}{{\mathrm{S}}_{\text{e}}} = \sum {\left( {\int_{{t_{\mathrm{s}}}}^{{t_{\mathrm{e}}}} {{p_{{\text{load}}}}} {\text{d}}t} \right)} $$ (12) 式中：
$ {\mathrm{EN}}{{\mathrm{S}}_{\text{e}}} $ ——系统能源缺供总量(kWh)；
$ {p_{{\text{load}}}} $ ——停止供能事故期间用户负荷需求预测曲线；
$ {t_{\text{s}}} $、$ {t_{\text{e}}} $ ——为停供事故起始时刻和结束时刻。
2)供能可靠率
供能可靠率指系统在实际运行过程中供能时间占比[41]，实际供能时间占比越大，则系统供能可靠性越高，表示为计算式（13）～式（14）：
$$ {\mathrm{SAT}} = \frac{{{T_{{\text{actu}}}}}}{{{T_{{\text{need}}}}}} \times 100\% $$ (13) $$ {T_{{\text{actu}}}} = {T_{{\text{need}}}} - \sum {{t_{{{{\mathrm{bla}},i}}}}} $$ (14) 式中：
$ {T_{{\text{actu}}}} $ ——用户实际年用能小时数(h);
$ {T_{{\text{need}}}} $ ——用户需求年用能小时数(h)；
$ {\mathrm{SAT}} $ ——年供能可靠率；
$ {t_{{\text{bla,}}i}} $ ——用户$ i $在全年供能故障总时长(h)。
3)系统平均故障停电时间
系统平均故障停电时间用于评估区域能源系统中电能可靠性。其定义为在一定时间内单个用户平均停电时间的期望[42]或单次停电的平均持续时间期望。表示为计算式（15）～式（16）：
$$ {T_{{\text{CAIDI}}}} = \frac{{{T_{{\text{user\_all}}}}}}{{{n_{{\mathrm{user}}}}}} $$ (15) $$ {T_{{\text{SAIDI}}}} = \frac{{{T_{{\text{user\_all}}}}}}{{{n_{{\text{ef}}}}}} $$ (16) 式中：
$ {T_{{\text{CAIDI}}}} $ ——用户平均停电时间(h)；
$ {T_{{\text{user\_all}}}} $ ——用户停电时间总和(h)；
$ {n_{{\text{user}}}} $ ——用户总数；
$ {T_{{\text{SAIDI}}}} $ ——系统平均停电持续时间(h)；
$ {n_{{\mathrm{ef}}}} $ ——系统停电总次数。
4)能源自给率
能源自给率表征区域能源生产满足消费的程度。能源自给率高，外依赖性小[43]。能源自给率表示为计算式（17）：
$$ {\lambda _{{\text{ES}}}} = \frac{{{E_{{\text{P1}}}} - {E_{{\text{OP}}}}}}{{{E_{{\text{EC}}}}}} $$ (17) 式中：
$ {\lambda _{{\text{ES}}}} $ ——能源自给率；
$ {E_{{\text{P1}}}} $ ——一次能源生产量(标准煤)；
$ {E_{{\text{OP}}}} $ ——对外能源输送量(标准煤)；
$ {E_{{\text{EC}}}} $ ——能源消费总量(标准煤)。
此外，能源自给率的计算通常不计对外能源输送量，表示为计算式（18）：
$$ {\lambda _{{\text{ES}}}} = \frac{{{E_{{\text{P1}}}}}}{{{E_{{\text{EC}}}}}} $$ (18) -
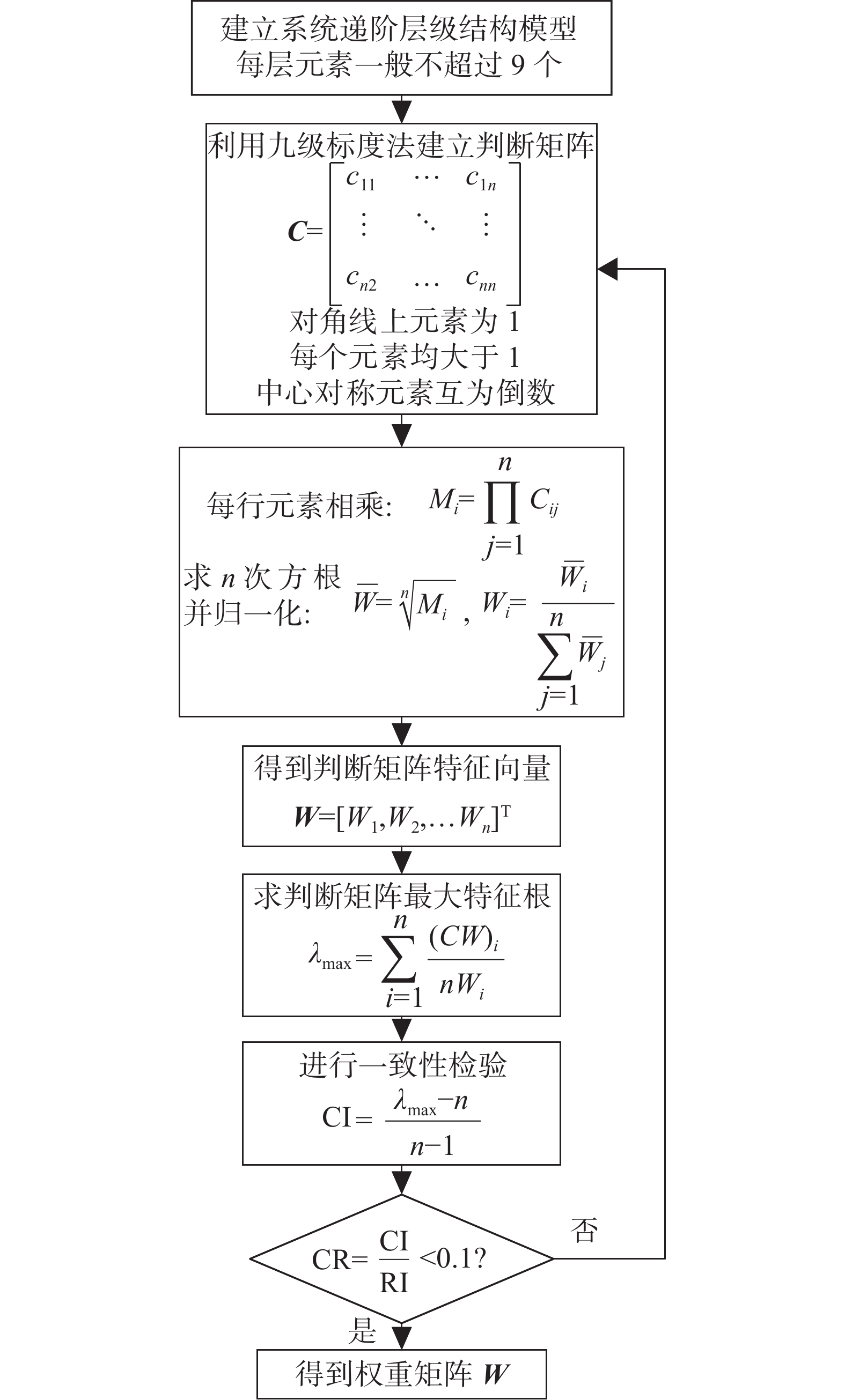
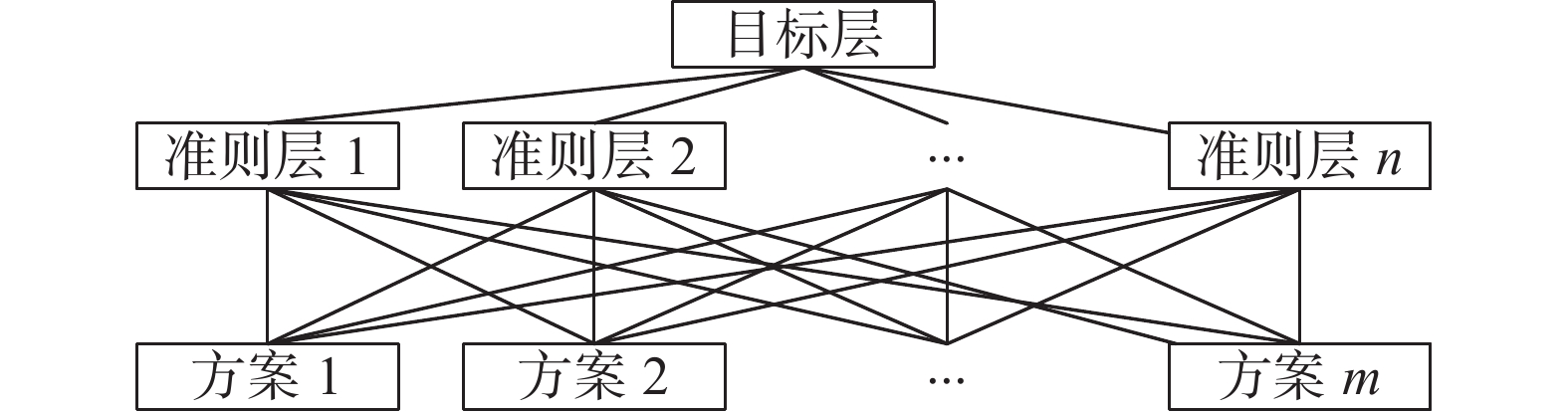
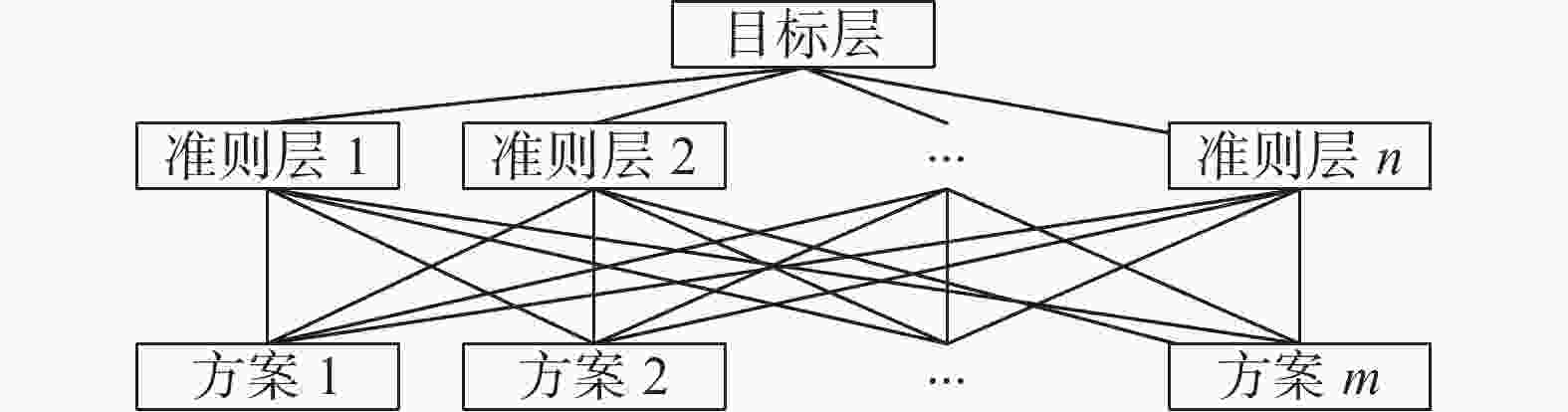
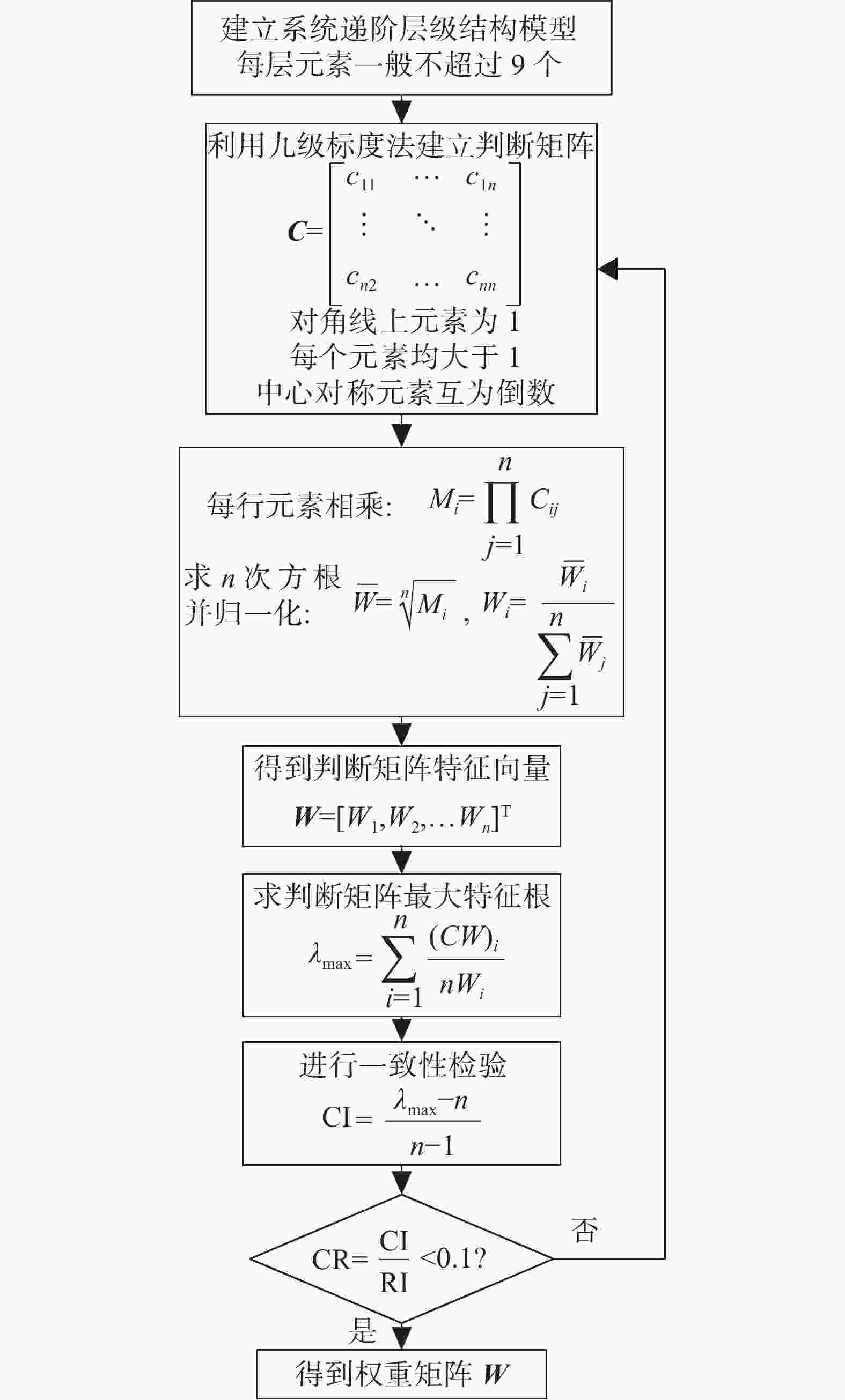
层次分析法适用于多目标并且包含定量定性问题，常用于对评价指标进行主观赋权，具有灵活、系统且简洁的特性[44]。层次分析法将评价系统分为如图1所示的层次结构。层次分析法的步骤如图2所示。
Figure 1. Hierarchy
步骤1和步骤2中，利用表3所示9级标度法对中同层中不同元素进行两两比较并构造判断矩阵。步骤3和步骤4求解了判别矩阵的权重向量，图2采用的是几何平均法。判别矩阵需要进行一致性检验，步骤5求取了最大特征根并在步骤6和步骤7进行一致性检验。其中，$ {\mathrm{CI}} $为一致性指标，$ {\mathrm{CI}} $越接近0越具有满意的一致性，$ {\mathrm{CI}} $越大，不一致性越严重。为了衡量$ {\mathrm{CI}} $的大小引入随机一致性指标$ {\mathrm{RI}} $。$ {\mathrm{RI}} $和判断矩阵的阶数$ n $有关，阶数越大，出现一致性随机偏离的可能性越大。$ {\mathrm{RI}} $取值如表4所示。最后通过判断一致性比率$ {\mathrm{CR}} $是否小于0.1判断是否有满意的一致性。判别矩阵的权重向量求解有多种方法。除几何平均法，还有特征向量法、和积法、幂乘法等[45]。
标度值 标度含义 1 i元素比j元素同等重要 3 i元素比j元素稍微重要 5 i元素比j元素明显重要 7 i元素比j元素强烈重要 9 i元素比j元素极端重要 2，4，6，8 上述相邻判断的中间标度值 倒数 若i元素对于j元素的标度值为aij，
则j元素对于i元素的标度值为ajiTable 3. Definition of the scale of the judgment matrix
Figure 2. The steps of analytic hierarchy process
n RI 1 0 2 0 3 0.52 4 0.89 5 1.12 6 1.24 7 1.36 8 1.41 9 1.46 Table 4. Average random consistency index
在区域能源低碳评价研究中，大部分研究对低碳技术、环境指标、能耗强度等指标赋予较大的权重，一方面反映了相关指标是区域能源低碳评价的关键，一方面反映了主观赋权法中决策者对低碳指标的偏好。区域能源低碳评价研究中通常需要从不同维度建立评价指标体系，且每个维度具有多个评价指标，层次分析法能够通过建立一个层次结构将众多指标进行排序，并通过9级标度法体现各种指标间的重要程度。层次分析法能够对区域能源状况进行总体把握，也能对各指标进行具体反映。层次分析法在能源低碳利用评价研究中具有较好的适应性，其构建层次结构的方法也常与其他评价方法结合。
-
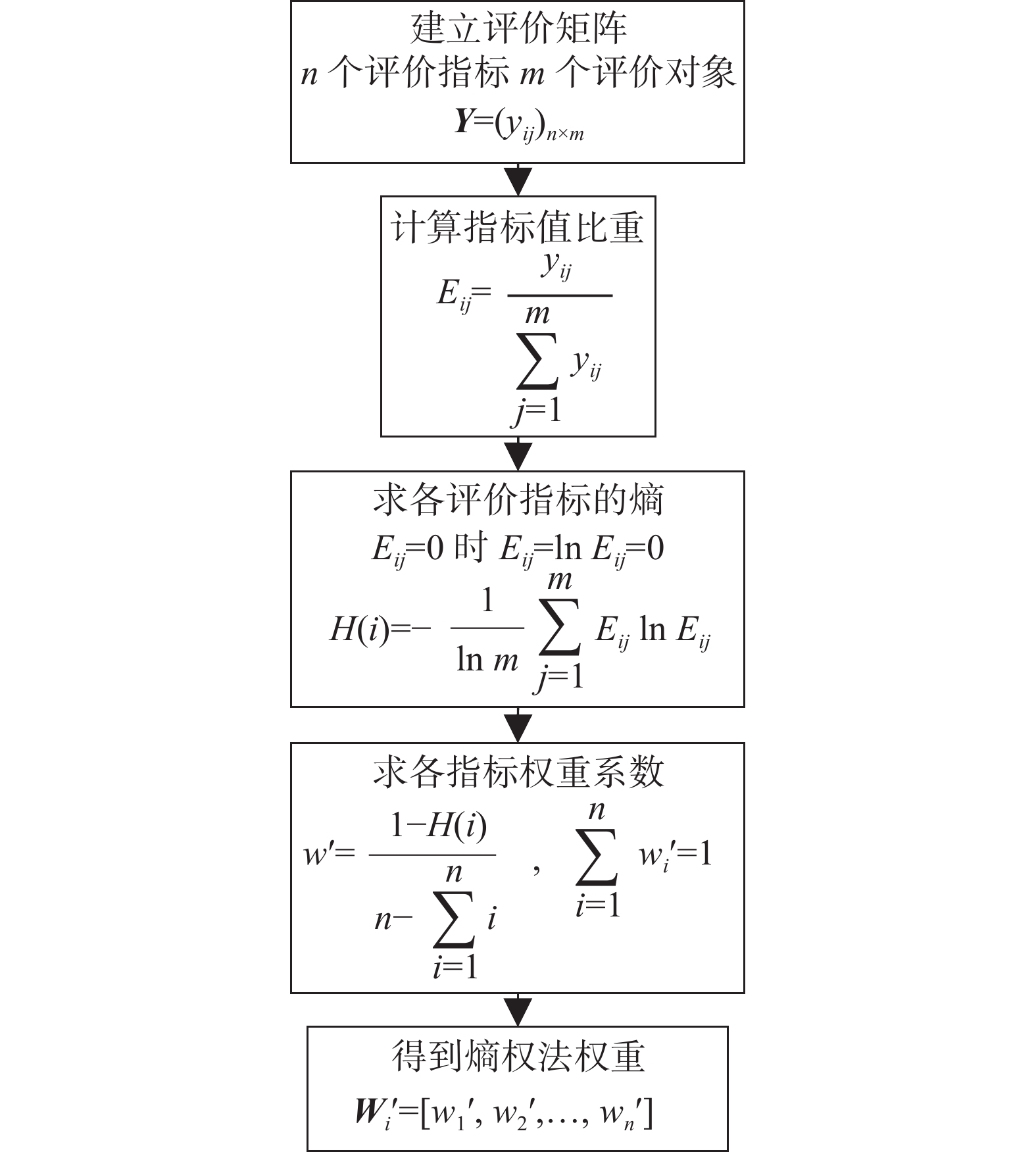
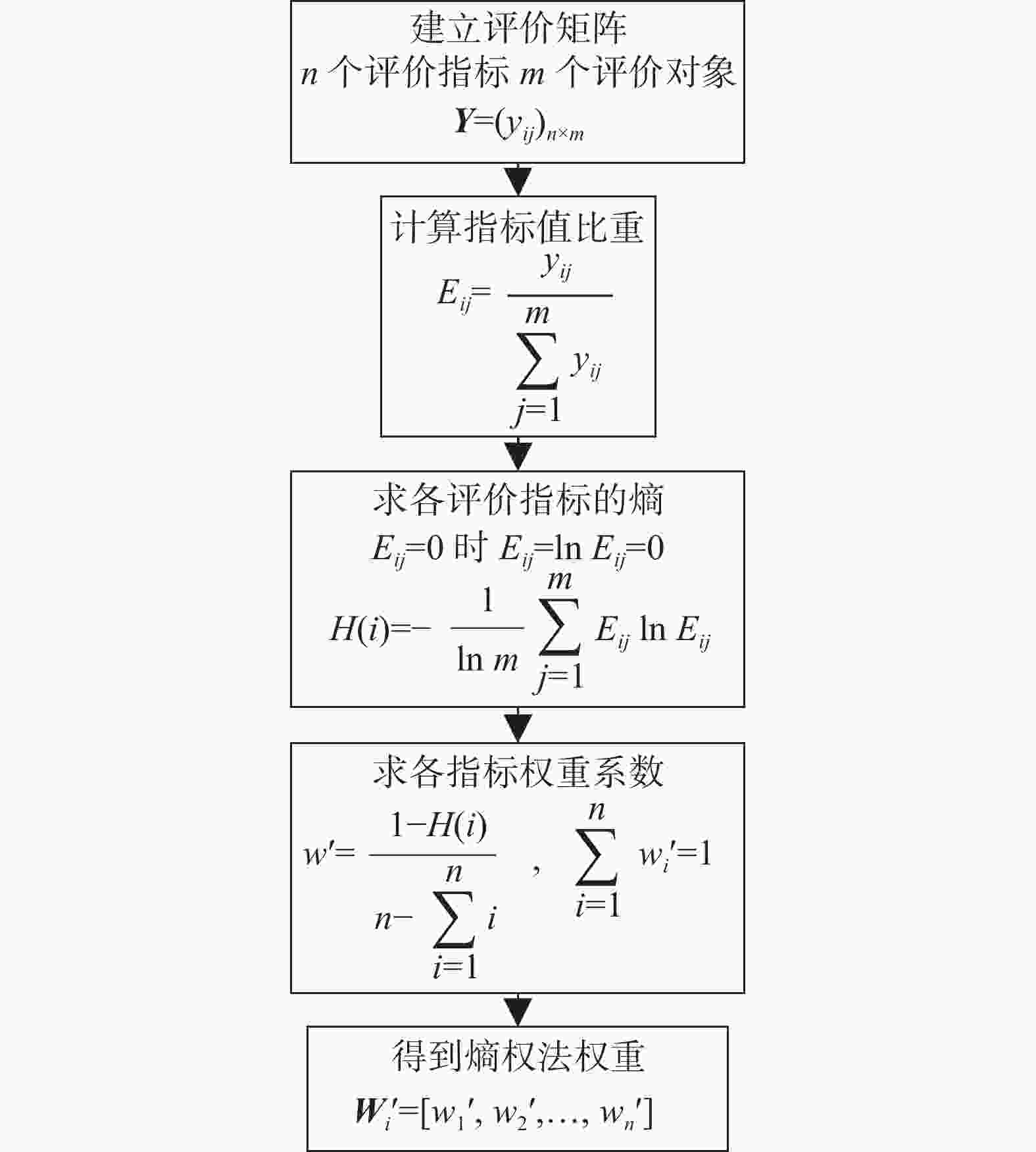
熵权法依据各指标包含信息量进行客观赋权。指标熵值越小，则表明指标变异程度大，提供信息量多，在综合评价体系中重要程度越大。因而该指标权重也应该越大[46-48]。
熵权法步骤如图3所示。在图3中，熵权法首先在步骤1建立评价矩阵，其中$ {y_{ij}} $为无量纲化的指标。在步骤2计算出每个指标值的比重后，步骤3进行了指标信息熵的计算。最后步骤4对各指标权重进行计算并得到权重向量。
Figure 3. The steps of entropy weight method
熵权法应用于能源低碳利用评价研究时，需要有足够的样本数据用于计算。因而在采用熵权法的评价研究中，相关评价指标如单位GDP电耗、人均碳排放量、工业SO2排放量等数据来源多为各类官方统计年鉴，以此保证样本数据量满足熵权法的适用要求。熵权法避免了赋权过程中主观性带来的不利影响，其通过数据本身包含信息量来决定权值，对数据变化情况较为敏感。该方法不需要建立层次结构，其计算方法较为简便易于操作，但有时需要面临计算量大的问题。同时在进行能源低碳利用评价研究时，需要根据实际情况对评价指标的重要程度进行判断，而熵权法仅根据数据的信息熵进行赋权，有时不能反映指标的实际重要程度。
-
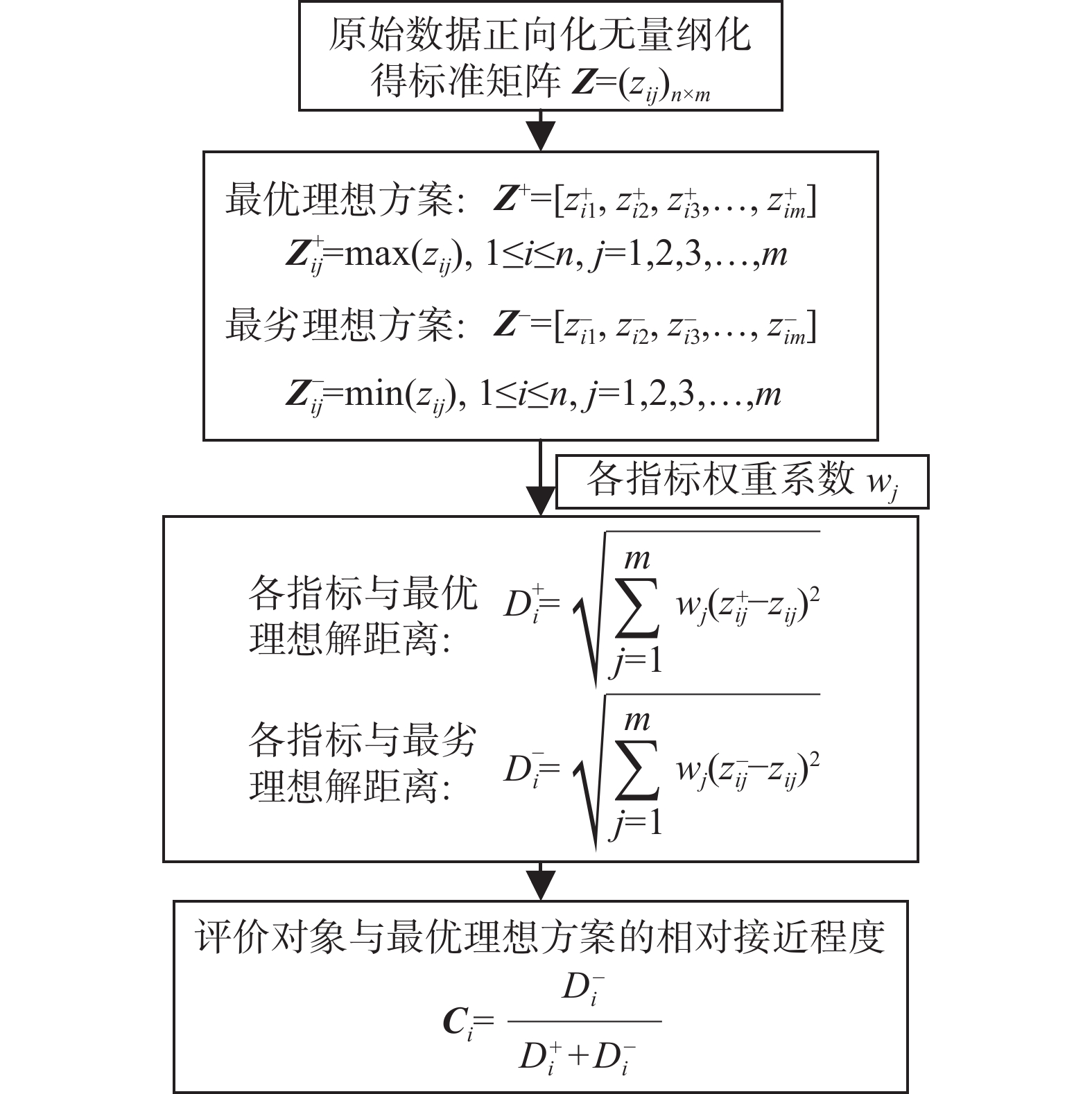
TOPSIS法属于一种统计分析方法，其具体步骤如图4所示。步骤1构造标准矩阵后，步骤2计算出最优与最劣理想方案，步骤3计算出各指标与最优最劣理想解的距离,步骤4计算评价对象与最优理想方案的相对接近程度。
Figure 4. Steps of TOPSIS method
该方法构造最优理想解和最劣理想解，以理想解相对距离作为决策判据，对现有评价对象进行排序与评价。该方法常配合层次分析法、专家打分法和熵权法[49-50]确定指标权重。该方法通过计算各指标与最优最劣理想解距离，将得分进行归一化并排序，数值越大，表明更优。
TOPSIS法常用于能源转型过程中的发展成效评价、低碳经济评价和低碳竞争力评价。该方法可通过指标历年数据，计算出最优方案贴近度$ {C_i} $的历年值，以此来反映在能源转型过程中低碳发展水平的变化。该方法也可通过构建层次系统，如分为低碳经济指标、低碳能耗指标、低碳环境指标等准则层指标，并计算各准则层指标的发展水平变化趋势，并结合能源低碳利用的发展水平总体趋势，对比分析各指标对整体发展水平的影响程度。
-
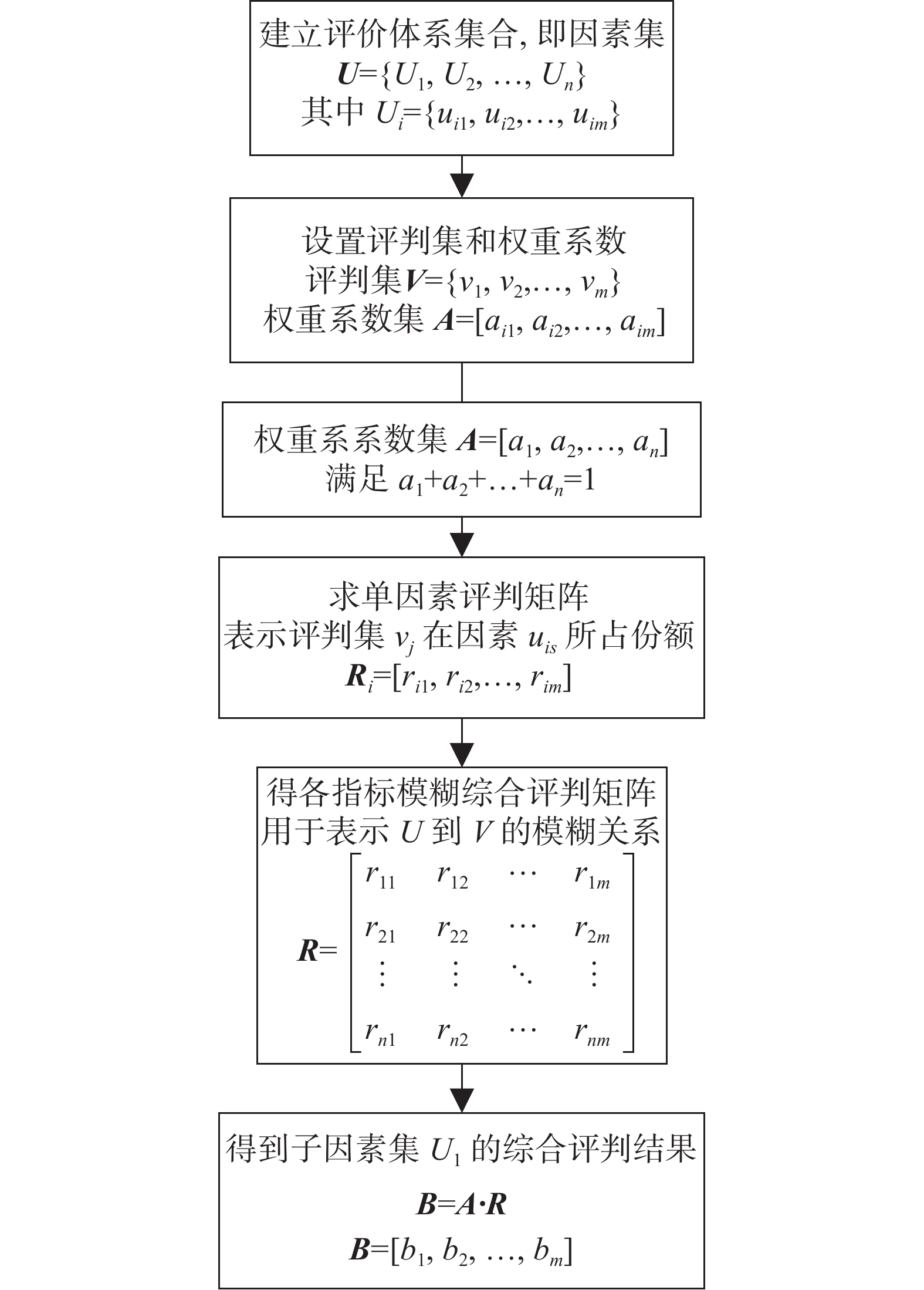
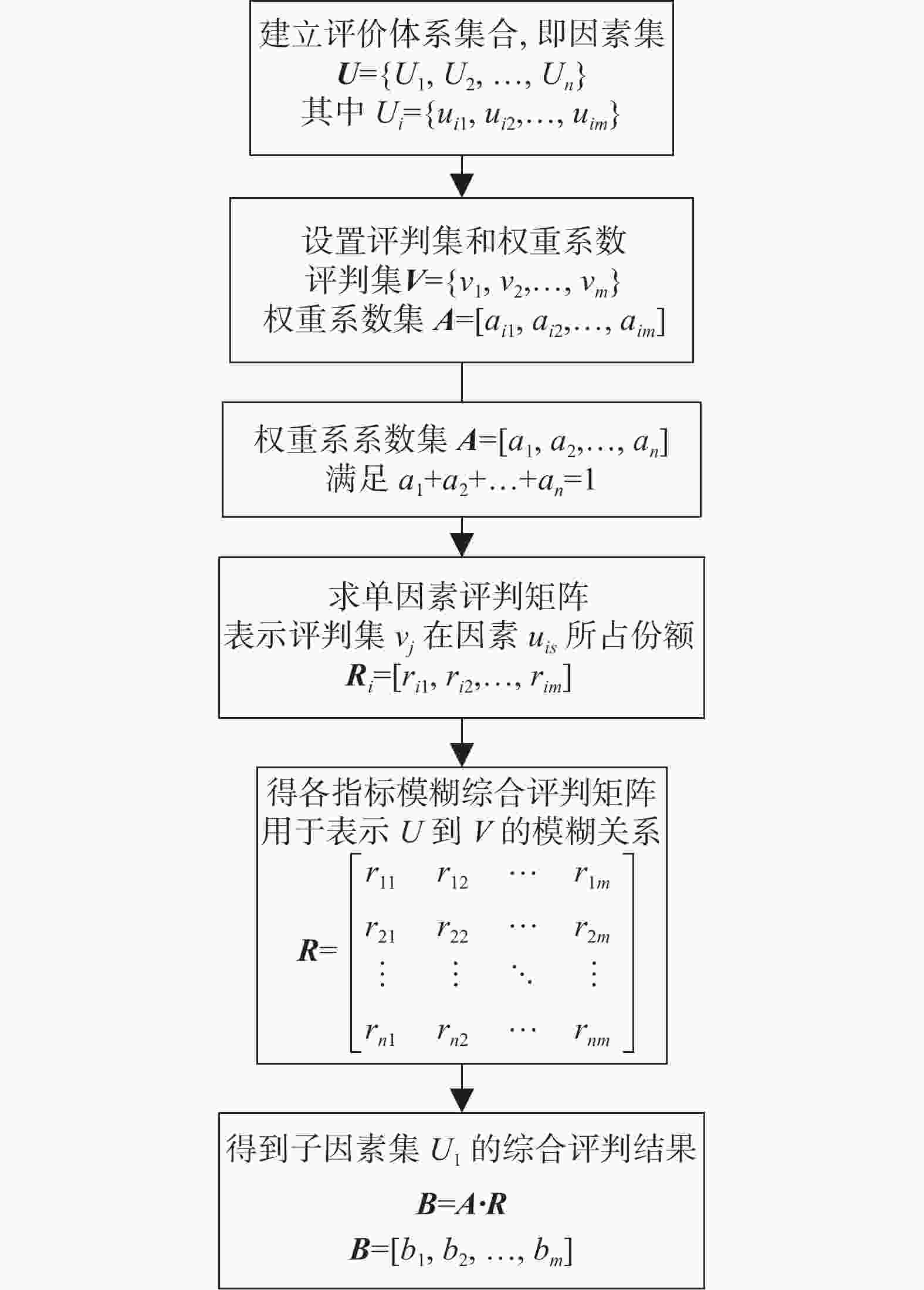
模糊综合评判法为主观赋权法。在综合评价过程中常需要面对多个指标并实现总体把握。该方法通过模糊数学中隶属度理论，将定性评价变为定量评价，适合用于解决非确定性问题。
其步骤[51]如图5所示。步骤1构建因素集，因素集$ {\boldsymbol{U}} $为由评价对象各因素组成的集合。步骤2构建评判集和权重系数集合。其中，评判集$ {\boldsymbol{V}} $为评价矩阵，由所有可能出现的评价组成；权重系数集$ {\boldsymbol{A}} $根据因素集中各因素重要程度分配权重。步骤3和步骤4通过专家打分构建模糊隶属度矩阵。步骤5和步骤6通过模糊判断矩阵与权重得到综合评判结果。
Figure 5. Fuzzy comprehensive evaluation method
在能源低碳利用评价研究中，各区域能源低碳发展水平各不相同，这对低碳利用评价研究带来了模糊性。能源低碳利用评价研究尚未有完整的评价体系，没有统一的评判标准。该情况下评价研究可采取模糊综合评判法，将评价指标分为成本型指标与效益型指标，通过调研所得的能源数据，构造以均值分界的逐级递减分布的隶属函数。该方法能在不确定性较强的情况下确定隶属度，对于评价能源低碳发展水平具有较好效果。模糊评判法在能源低碳利用评价研究中仍然具有一定的适应性。
-
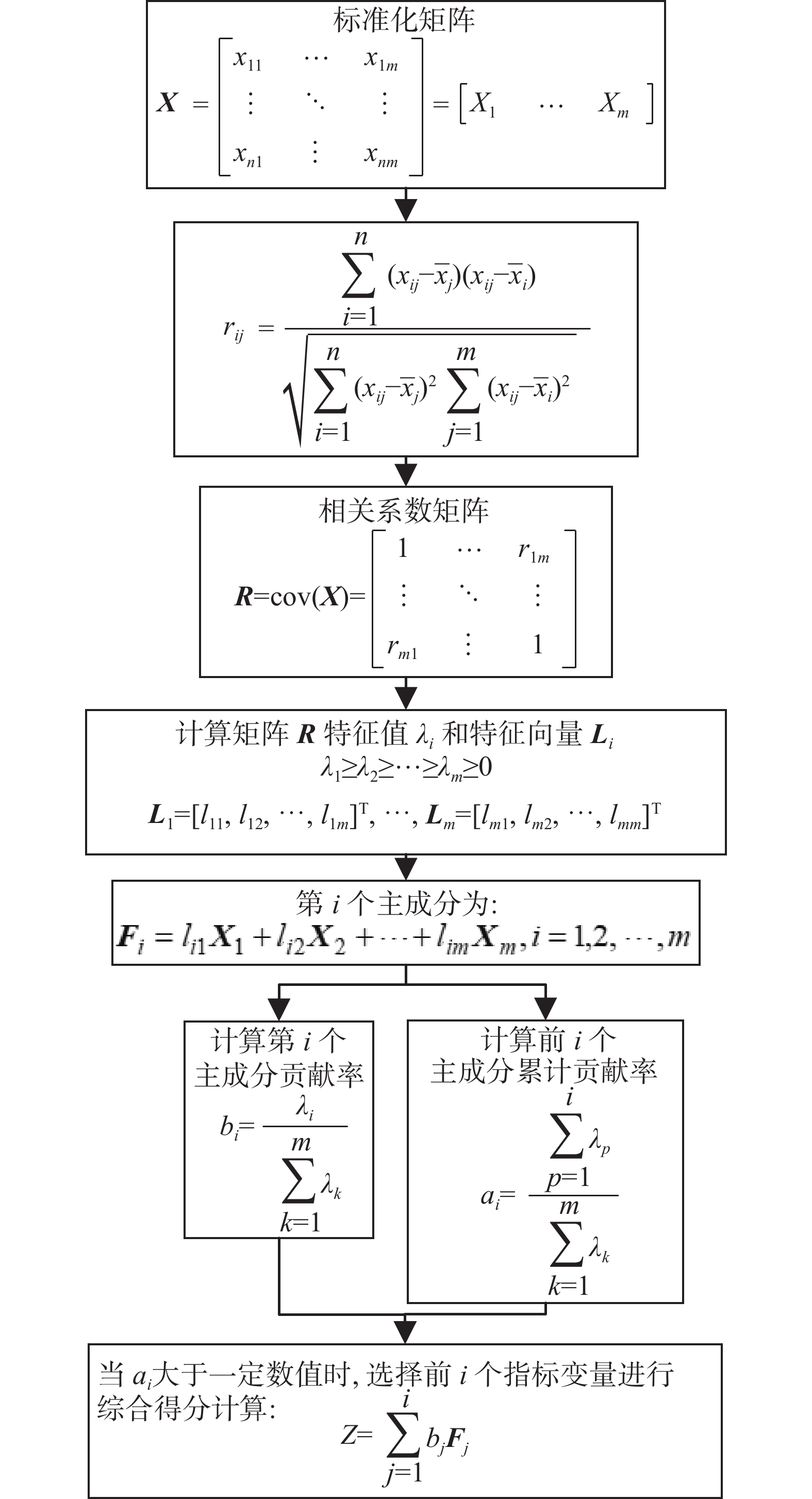
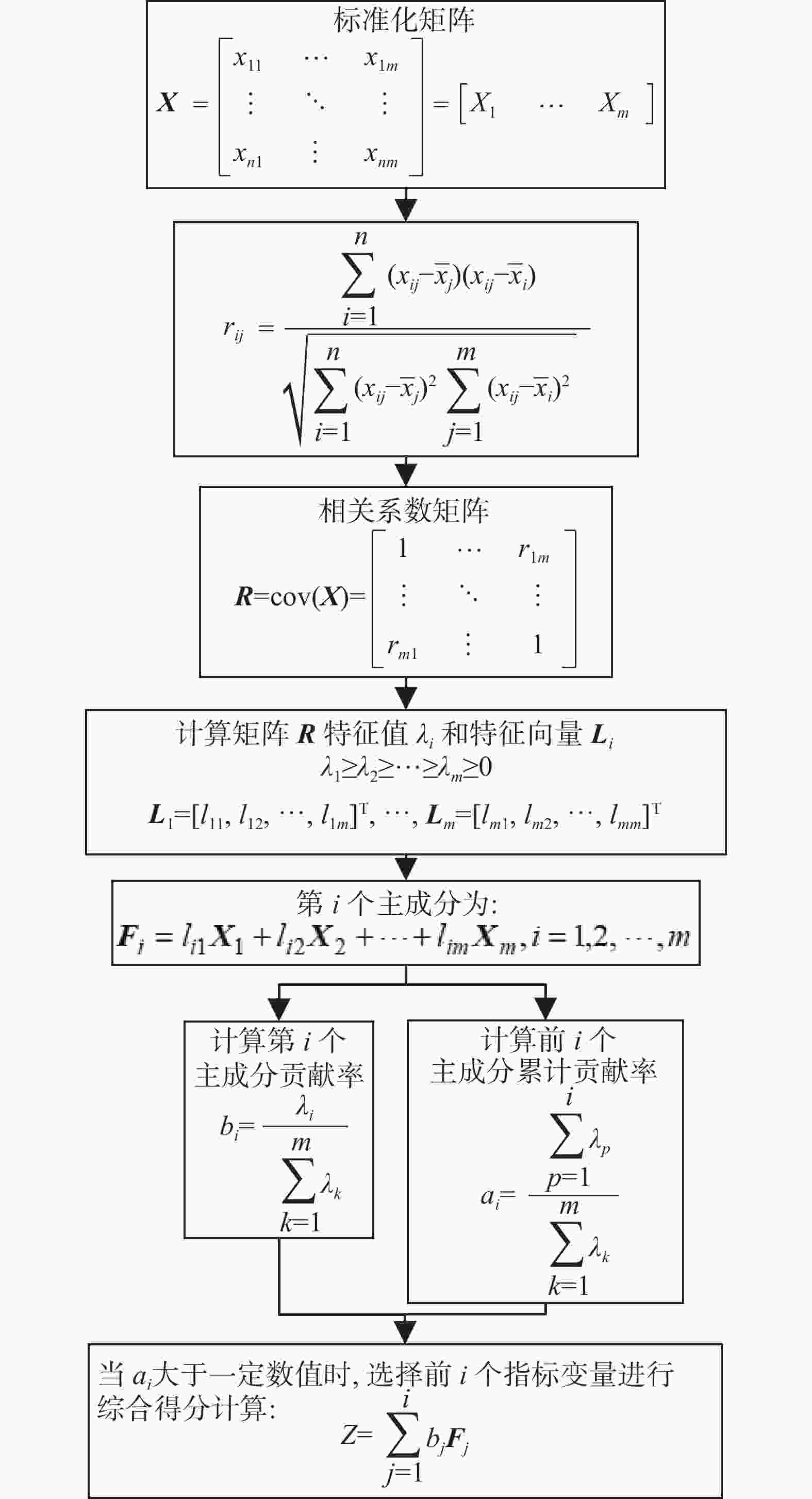
主成分分析法通过转化变量，使得多个相关变量变为少量不相关的综合指标，降低评价指标和庞大数据处理难度，提高分析效率[52]。主成分分析法具体步骤如图6所示。
Figure 6. Principal component analysis method
步骤1对原始数据归一化得到矩阵$ {\boldsymbol{X}} $。步骤2和步骤3对协方差矩阵$ {\boldsymbol{R}} $即相关系数矩阵进行计算。步骤4和步骤5对相关系数矩阵的特征向量和特征值进行计算，用于识别主成分。步骤7在步骤6的基础上，确定主成分个数，通常当$ {a_i} > 0.85 $时，选择前$ i $个指标变量作为$ i $个主成分并进行综合得分的计算。
主成分分析法在能源低碳利用评价研究中，可通过其数据降维的方式，从指标体系中归纳出主要的能源低碳利用评价指标，得到新的评价指标体系，提高能源低碳利用评价的科学性。相关研究通常在原有的评价指标体系中使用主成分分析法，并将得到的各主成分重新定义，赋予类似层次分析法中准则层指标的含义。主成分分析法根据指标间的相关性，使用较少的指标来反映原指标体系的大部分信息，优化了能源低碳利用评价指标的构建，在能源低碳利用评价中具有较好的效果。
-
层次分析法和模糊综合评判法都属于主观赋权法。层次分析法把定性的指标通过标度值定量化，但在应用过程中具有随机性以及评判的主观性。模糊综合评价借助主观判断的方式通过模糊隶属度将涉及模糊因素的指标定量化。主观赋权法需要对评价对象各指标的重要程度和逻辑关系了解透彻，尽量避免主观性带来的偏差。该方法在对包含定性指标、缺乏必要数据和结构复杂的评价具有较好效果。两者之间也存在各自的特点：层次分析法在能源低碳利用评价研究中的应用较为广泛，其构建层次结构的方法可结合多种评价方法使用，更加适用于能源评价指标体系较为复杂的情况；模糊综合评判法则适用于评判能源低碳发展水平，在没有统一评判标准时划分评判的界限，更适合处理不确定性较大的评价对象或者对能源系统的不同规划时期进行分析评价。
熵权法和主成分分析法都属于客观赋权法。熵权法通过计算各指标的熵得到权重；主成分分析法通过综合因子的贡献率进行赋权。客观赋权法根据原始数据进行计算得到权重，主观性小。熵权法对样本依赖性大，未考虑指标间相关性，主成分分析法对样本数量的要求较大。客观赋权法在数学理论方面有坚实基础。然而，该类方法无法包含决策者对不同属性的偏好，有时可能导致确定的权重与指标的实际重要程度不符。熵权法与主成分分析法虽同属客观赋权法，但其作用各不相同：熵权法在能源低碳利用评价研究中常常与层次分析法结合形成主客观赋权，弥补熵权法无法体现评价指标实际重要程度的缺点；主成分分析法在能源低碳利用评价研究中应用广泛，该方法适用于多指标的研究，在能源低碳利用评价过程中，常常需要涉及包含各类低碳指标、效率指标，主成分分析法能对信息重叠的指标进行处理，形成简洁的指标体系，对于构建能源低碳利用评价指标体系具有很好的适应性。
客观赋权法基于能源碳排放和能源利用效率等数据进行准确的评估，而在实现能源转型的过程中，能源低碳利用的评价有时需要结合具体的发展需求，因此可通过主观赋权的方式反应决策者主观意愿。综合运用两种方法，可以更全面、准确地评估了解能源低碳利用的情况。
TOPSIS法的权值是由其他方法确定的。TOPSIS法通过计算各指标与最优最劣理想解的距离作为评价优劣的依据，在评价过程中可根据评价对象的情况结合多种方法使用。该方法常应用于对区域在能源转型过程中的低碳发展水平进行评估，其水平优劣情况直接从最优方案贴近度的历年变化中反映出来，评价结果直观。TOPSIS法适用于能源低碳利用评价研究中同一对象不同时间、同一时间多个对象、同一对象不同准则层指标三种场景的评价研究，具有很强的适应性，且能分别体现出各指标贴近度与总体发展水平贴近度的变化趋势，辅助决策者进行进一步分析。
-
本文首先综述能源评价技术研究，将评价对象分为能源系统和区域性能源，分别总结其特点。接着从能源低碳指标、能源利用指标和能源安全指标3个方面对低碳利用评价指标进行总结。最后对常用评价方法进行梳理，分析不同评价方法的优劣，结合具体需求，采用适当的评价方法，能更好了解能源低碳利用的情况。
当前能源低碳利用评价还未出现针对性研究，通常只作为评价指标体系的一部分进行低碳评价。随着低碳能源的发展、清洁能源占比的提升，低碳能源利用进行评价的重要程度将越来越大。能源的低碳利用评价技术将在“双碳”战略推进下逐渐丰富与发展。
Review of Evaluation Indicators and Technologies for Low-Carbon Energy Utilization
doi: 10.16516/j.ceec.2024.5.19
- Received Date: 2023-08-17
- Rev Recd Date: 2023-09-12
- Available Online: 2024-09-30
- Publish Date: 2024-09-10
Abstract:
| Citation: | GAO Chao, WEI Bin, SUI Yu, et al. Review of evaluation indicators and technologies for low-carbon energy utilization [J]. Southern energy construction, 2024, 11(5): 178-190 doi: 10.16516/j.ceec.2024.5.19
|
DownLoad:
