-
风场发电量是决定风电场投资决策的关键因素之一,是影响风场经济效益的重要指标。因发电量的评估是根据测风数据经过长期代表年订正后,通过流体力学模型软件推算到风场各风机点位轮毂高风速,再结合风机功率曲线预测风场全生命周期的平均产量水平。在利用过去已有测风数据评估未来建成风场产量这一过程中,每一环节都将给发电量带来不确定性,且测算时间距离评估风场时间越远,风场地形地貌越复杂预测的不确定性会越大。因此,发电量的不确定性是客观存在的,对它进行正确的分析和评估,采用一定超越概率下的发电量评估结果有助于降低风场投资风险,使决策建立在正确、可靠的基础上[1]。
对于影响风场发电量不确定性因素国内风电企业及设计单位普遍不做单独考虑,而是对影响发电量的各因素估算一定比例,在总发电量的基础上“折减”,将发电量不确定性转换为折减系数计算折减电量,最后得到预估发电量[2]。这种方法很大程度上取决于评估人员的风险偏好,折减系数难以与实际情况相匹配,采用“折减系数”法是一种迂回控制不确定性因素给项目带来风险的简单方法,不能反映出风险本质,计算结果可靠性差。
国外的风电企业普遍将发电量不确定性与折减分开考虑,Matthew等[3]提出了风场发电量评估过程中存在高度不确定性,将风速不确定性因素分为14类和风机功率曲线不确定性因素分为3类,给出了不确定性因素的计算公式,采用各不确定因素平方和的方法计算发电量总体不确定性因子,再计算超越概率发电量。
Birgir和Gudmundur将蒙特卡洛模拟法用于风场中模拟风速威布尔分布从而评估风场产量,并将其模拟风速计算所得产量与实测风数据所得产量进行比较,其结果相差较小,得出蒙特卡洛模拟法模拟风速计算的产量结果具有可靠性[4]。
计算不确定性因素带来发电量偏差是风资源评估不可或缺的内容,是判别项目风险的重要依据[5]。为了降低发电量偏差给投资带来风险,采用超越概率发电量作为投资决策的依据,文章针对目前风场发电量不确定性评估中存在的问题,假设每个不确定因素是独立的且服从正态分布,建立不确定性因素的正态分布模型,利用蒙特卡洛模拟法对这些不确定性因素进行模拟,得到统计值,再通过发电量敏感因子将这些不确定性程度转化为发电量不确定性程度,在此基础上计算风场超越概率发电量。
-
对不确定性作定量分析称为不确定性评估,常用的评估方法有确定性概率分析法和蒙特卡洛模拟法[2]。不确定性因素属于随机变量,这些随机变量通常采用某一概率模型分布来描述,由于这类模型含有不确定性的随机因素,分析起来通常比确定性的模型困难。有的模型难于作定量分析,得不到解析结果,或者是虽有解析的结果,但由于蒙特卡洛模拟法的计算精度与样本量的平方根成正比,故需要的样本量很大,模拟次数一般在数万次到几十万次才能保证计算精度,过去认为蒙特卡洛模拟法计算时间长,限制了它的使用,但随着计算机技术的发展,现在采用蒙特卡洛模拟法很容易解决这类随机概率模型问题[6]。
-
蒙特卡洛模拟法又称为统计模拟试验法或随机模拟法,它是以概率论和数理统计为基础,通过计算机随机模拟,用统计方法估计和描述随机变量的统计量、求解问题近似解,从而得到实际问题的数值解的一种数值计算方法[7]。常被用于解决那些无法通过确定性算法得到表达式或数值解的问题,在数理问题、各类工程领域甚至经济金融领域都有广泛应用[5]。
蒙特卡洛模拟方法运用在此文章的基本思路是假设所有引起发电量的不确定性参数是相互独立且服从正态概率分布的模型[8],在计算机上模拟这些概率模型,由给定的模型直接产生一大批数据样本,用研究这些样本的性质代替对不确定性模型本身的研究,将求解不确定性问题转换为求解这些样本的参数统计值(如均值、标准差、中位数等),从而得到不确定性程度,求解的精度可用方差来表示[6]。
-
风场发电量的不确定性主要来源于测风数据、风资源评估软件、功率曲线3大因素。
测风数据处理是风场发电量计算过程首要且较为耗时的重要工作。这一阶段从测风传感器的选择到测风塔的安装设立,测风时间的长短和测风数据质量及长期代表年的订正,每一环节都将引起风速的不确定性,从而给发电量评估带来不确定性。
在利用风资源评估软件从测风塔位置风况推算风场各风机点位轮毂高度风况时,会引起垂直和水平外推不确定性,其不确定性程度取决于测风塔代表性高低,垂直外推的不确定性程度与测风塔处的海拔高度和风机点位处的海拔高度差呈正向关系,也与测风高层与轮毂高层高度差呈正向关系,高度差别越大,其不确定性就越高。水平外推的不确定性程度取决于测风塔位置与风机位置的水平距离。
风机功率曲线表示风机在不同风速段出力效果,风机功率曲线需要按照规定程序进行测试。因功率曲线测试时的环境与风场风机运行的实际风流环境不同带来的不确定性,环境包括地形地貌和风机排布及周边邻近风场。取得认证的风机功率曲线不确定性一般取值4%~6%[9]。风场发电量不确定性影响因素如表1所示。
不确定性类别 不确定性因素 不确定性因素来源 建议取值 取值参考文献 测风数据 风资源测量 传感器类型 1%~6% [9] 传感器校准 0.5%~2.06% 测风塔塔架形式 0.50% 长期代表年订正(MCP) 实测测风塔数据时间长短 1%~4% [10] 长期参考数据时间长短 2%~8% 实测测风塔数据与长期数据相关性高低 0.9<R2,<1% [11] 0.9>R2>0.8,1%~2% 0.8>R2>0.7,2%~3% 0.7>R2>0.6,3%~5% 未来气候 未来气候的变化 5% [12] 风资源评估软件 垂直外推 测风塔海拔与风机点位海拔差距 简单平坦地形0.05%/10 m;山地丘陵0.3%/10 m [10] 测风高度与风机轮毂高度差距 简单平坦地形0.3%/10 m;山地丘陵1.0%/10 m 水平外推 测风塔位置与风机位置的水平距离 简单平坦地形0.5%/km;山地丘陵1.5%/km 以上各指标的不确定性大小皆引起风速值变化大小,下面的风机功率曲线不确定性程度直接影响发电量变化大小 风机功率曲线 风机功率曲线 标准认证 4%~6% [9] Table 1. Uncertainty factors of power generation
-
假设表1中各不确定性因素是相互独立且服从正态分布的随机变量,其数值不能精确地预测和计算,实际发生值总是与预测值有一些偏差,是一个随机变量或随机变量函数,任一不确定性参数的值,可用趋势值与具有某种概率分布的偏差来表达。文章将不确定性因素定义为服从平均值μ和偏离程度σ的正态概率分布[13],不确定性因素的正态概率分布函数和风速总不确定性程度的模型表达式分别如式(1)和式(2)所示:
$$ {U_i} = \frac{1}{{\sigma \sqrt {2\pi } }}\exp \left( - \frac{{{{({\textit z} - \mu )}^2}}}{{2{\sigma ^2}}}\right) $$ (1) $$ \begin{split} &{U_{\mathrm{v}}} =\\& \sqrt{{U_1}^2 + {U_2}^2 + {U_3}^2 + {U_4}^2 + {U_5}^2 + {U_6}^2 + {U_7}^2 + {U_8}^2 + {U_9}^2 + {U_{10}}^2} \end{split} $$ (2) 式中:
Ui ——n个相互独立的随机变量$ ({U}_{1},{U}_{2},{U}_{3}\cdots, U{}_{n}) $,分别服从正态分布$ {U_i}\sim({u_i},{\sigma _i}^2) $;
Uv ——风速带来的总不确定性程度(%);
U1 ——传感器类型带来的不确定性程度(%);
U2 ——传感器校准带来的不确定性程度(%);
U3 ——测风塔塔架形式带来的不确定性程度(%);
U4 ——实测测风塔数据长短带来的不确定性程度(%);
U5 ——长期参考数据时间长短带来的不确定性程度(%);
U6 ——实测测风塔数据与长期参考数据相关性高低带来的不确定性程度(%);
U7 ——未来气候变化带来的不确定性程度(%);
U8 ——测风塔海拔与风机点位海拔差距带来的不确定性程度(%);
U9 ——测风高度与风机轮毂高度差距带来的不确定性程度(%);
U10 ——测风塔位置与风机位置的水平距离带来的不确定性程度(%)。
-
若对不确定性因素变量$ {U_1},{U_2},{U_3}......,U{}_n $进行一次随机抽样,便可得到一组包含$ {U_1},{U_2},{U_3}......,U{}_n $变量值,这里对不确定性因素Ui随机抽样可采用Excel中复合函数NORMINV [RAND(probability), mean, standard_dev]实现,其中NORMINV函数的功能是根据指定平均值和标准差计算正态累计分布的反函数值;RAND(probability)为随机函数,概率取值范围在0~1之间。蒙特卡洛模拟法的计算精度与抽样次数成正比,若经过N次抽样和运算,随着抽样次数增加,影响风场风速的不确定性样本分布便趋近于总体分布[14-15],即重复次数越多,模拟结果与实际情况越相近[16]。利用概率统计便可得出影响风场风速不确定性Uv的概率分布平均值、标准差等参数。
计算风速不确定性评估时,可借助Excel中模拟运算What-If Analysis来解决,What-If Analysis是一种多次运算组合模拟参数使得目标函数得到统计的解决办法,且不需要R语言或Matlab这样的编程设计,此方法结构简单、模拟过程灵活,方便快捷,能提高计算的效率和准确性[17]。
-
风速-发电量敏感因子是借用经济学中价格-需求弹性系数的含义来描述风场因风速变化导致发电量变化,不同的风场其风速-发电量敏感因子不同,影响风速-发电量敏感因素有:平均风速、风频分布、风机排布、风机机型[18]。计算时用改变输入风资源评估软件中的风速序列或矩阵,其余输入量和模型参数设置保持不变,通过试算得到。公式如下:
$$ S = {{\frac{{({E_{{v_2}}} - {E_{{v_1}}})}}{{{E_{{v_1}}}}}} \mathord{\left/ {\vphantom {{\frac{{({E_{{v_2}}} - {E_{{v_1}}})}}{{{E_{{v_1}}}}}} {\frac{{({v_2} - {v_1})}}{{{v_1}}}}}} \right. } {\frac{{({v_2} - {v_1})}}{{{v_1}}}}} $$ (3) 式中:
S ——风速-发电量敏感因子;
$ {E}_{{v}_{1}} $ ——风速为v1时发电量(GWh);
$ {E}_{{v}_{2}} $ ——风速为v2时发电量(GWh)。
-
据第1章节发电量不确定性影响因素分析,有10个因素是因为引起风速的不确定性而影响风场发电量不确定性,风速与发电量关系不是线性关系,文章通过2.1章节风速-发电量敏感因子将风速不确定性转化为发电量不确定性,具体见式(4):
$$ {U_v}(E) = S \times {U_v} $$ (4) 式中:
$ {U_v}(E) $——风速不确定性带来的发电量不确定性大小(%)。
风机出力大小直接影响发电量多少,在计算风机功率曲线标准认证不确定性带来的发电量不确定性程度时,功率曲线的不确定性程度等于发电量不确定性程度。
$$ {U_p}(E) = {U_p} $$ (5) 式中:
$ {U_P}(E) $ ——功率曲线不确定性带来的发电量不确定性程度(%);
$ {U_P} $ ——功率曲线不确定性程度(%)。
风场发电量不确定性程度由风速和功率曲线两部分决定,结合式(4)和式(5),风场发电量总不确定性程度计算公式如式(6)所示:
$$ {U}_{T}(E)=\sqrt{{U}_{v}{(E)}^{2}+{U}_{p}{(E)}^{2}} $$ (6) 式中:
$ {U_T}(E) $——风场发电量总不确定性程度(%)。
-
水电水利规划设计总院发布的《关于对中国风电发电量折减问题的说明》[19],此说明对风电场理论发电量和风电场净发电量进行了定义,风场需根据实际情况考虑折减系数,通过风资源评估软件计算出的发电量为理论发电量,此理论发电量扣除折减后为净发电量,其计算公式见式(7):
$$ {E_{{\mathrm{net}}}} = {E_{{\text{gr}}{\mathrm{oss}}}} \times {F_{{\mathrm{loss}}}} $$ (7) 式中:
Enet ——净发电量(GWh);
Egross ——理论发电量(GWh);
Floss ——折减系数。
文章将折减和不确定性分别考虑,在风场理论发电量扣除折减后得到风场净发电量,以此基数进行后续的超越概率发电量计算。
考虑风场各因素的不确定性,根据式(6)计算得到风场发电量总不确定性程度$ {U_T}(E) $。风场发电量服从正态分布[20],风场发电量的标准差及不同概率相应的产量计算分别见式(8)和式(9):
$$ {\sigma _E} = {U_T}(E) \times {E_{{\mathrm{net}}}} $$ (8) $$ E_{P_x}=E_{P_{50}}\times (1-\mathrm{NORMSINV}({P}_{x})\times {\sigma }_{E}) $$ (9) 式中:
$ {\sigma _E} $ ——风场发电量分布的标准差(GWh);
$ E_{P_x} $ ——概率为$ {P_x} $时的发电量(GWh);
$ E_{P_{50}\;} $——风场发电量分布平均值,概率为50%的发电量,其值等于$ {E_{{\mathrm{net}}}} $(GWh);
$ {\mathrm{NORMSINV}}({P_x}) $ ——标准正态分布概率为$ {P_x} $的置信区间。
-
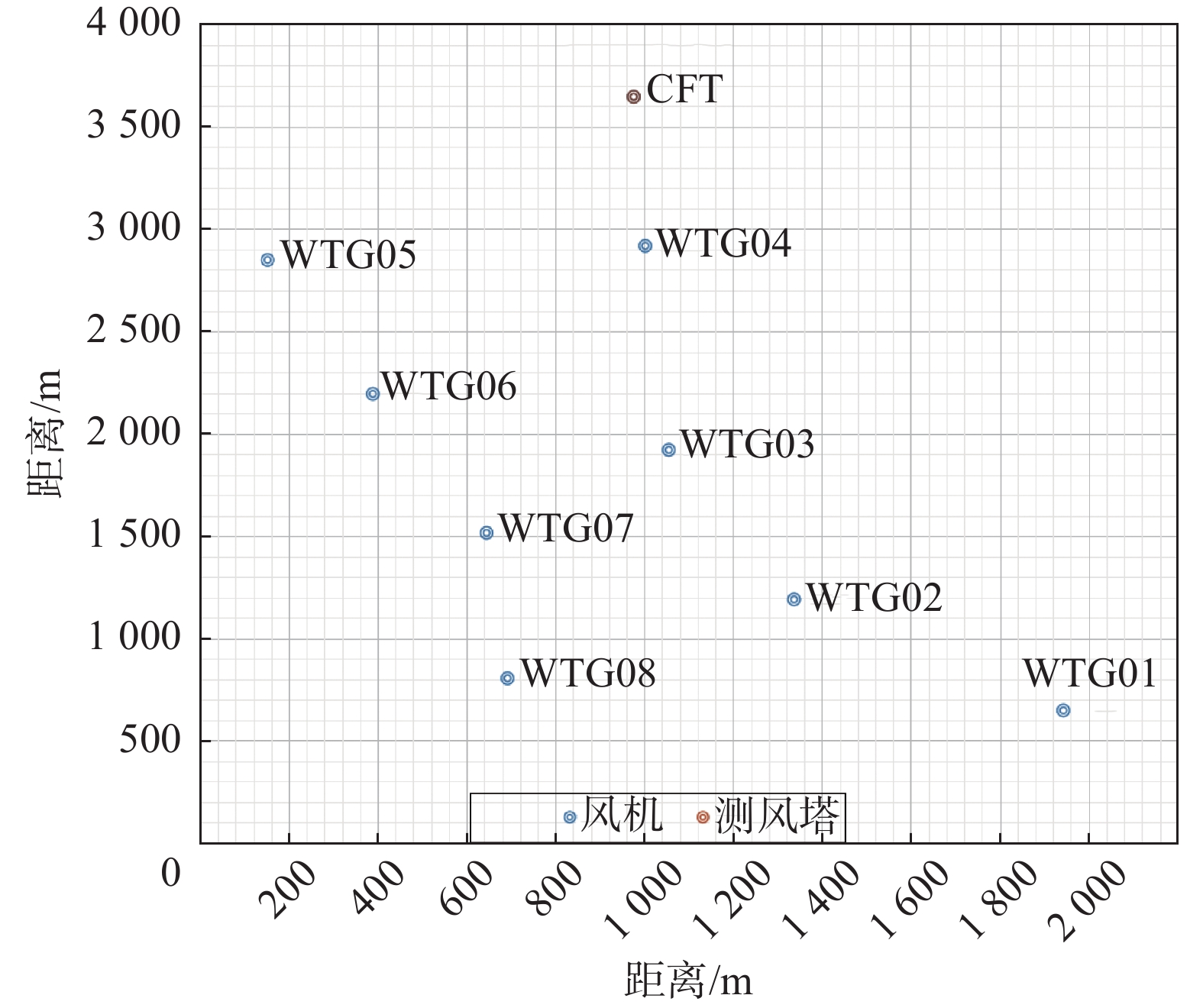
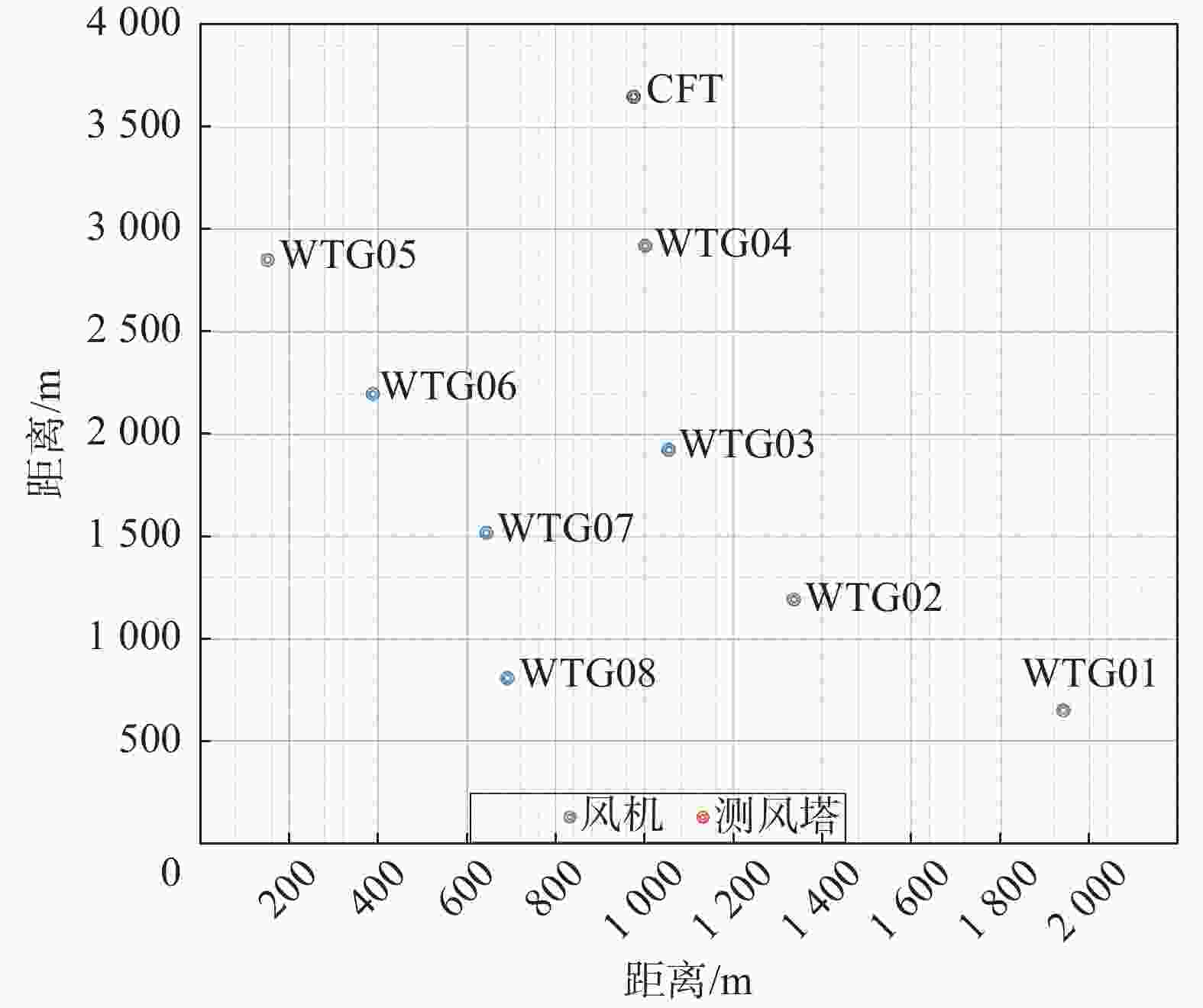
风场位于丘陵地区,规划容量50 MW,拟安装8台容量为6.25 MW风机,轮毂高度为115 m;场区内立有1坐110 m高测风塔,风速测量采用美国NRG40#风杯,仪器经过标准校准,塔架采用桁架式;测风数据满2 a且数据有效率达95%,长期参考数据满20 a,实测测风数据与20 a长期参考数据做相关,相关系数R=0.87;测风塔在115 m、100 m、90 m、70 m、50 m、10 m高层安装了风速仪,在115 m、50 m、10 m高层安装了风向标;测风塔海拔高度184 m,风机位置机位点海拔平均值245 m;测风塔到风机位置的平均距离为5 km,测风塔与风机位置布置如图1所示。
-
根据文章3.1小节描述的风电场实际情况,测风塔实测数据的测风时间长短及质量,长期参考站数据与实测数据相关性高低,以及测风塔对风机位置的代表性等资料数据。参考表1的不确定性因素来源及分析进行取值,各不确定性因素服从正态分布,其均值和标准差如表2所示。标准差根据IEC国际标准设置了低中高3种,分别为平均值的12.0%、14.0%和16.0%[21]。
不确定性因素 平均值μ 标准差$ \sigma=0.12\mu $ 标准差$ \sigma = 0.14\mu $ 标准差$ \sigma = 0.16\mu $ 标准差 随机模拟 标准差 随机模拟 标准差 随机模拟 传感器类型 2.00 0.24 2.14 0.28 2.06 0.32 2.52 传感器校准 1.48 0.18 1.71 0.21 1.82 0.24 1.45 测风塔塔架形式 0.50 0.06 0.40 0.07 0.60 0.08 0.48 实测数据时间长短 2.00 0.24 1.63 0.28 2.03 0.32 2.47 长期参考数据时间长短 3.00 0.36 3.16 0.42 3.16 0.48 2.74 实测数据与长期数据相关性高低 3.00 0.36 2.71 0.42 3.39 0.48 3.44 未来气候变化 5.00 0.60 4.55 0.70 5.24 0.80 5.28 测风塔海拔与风机点位海拔差距 0.25 0.03 0.21 0.04 0.30 0.04 0.26 测风高度与轮毂高度差距 1.00 0.12 0.84 0.14 0.98 0.16 1.00 测风塔位置与风机位置水平距离 2.50 0.30 2.54 0.35 2.43 0.40 2.68 风速总不确定性程度 7.79 7.48 8.12 8.37 Table 2. Normal distribution of uncertainty factors and the first stochastic simulation
% 利用函数NORM.INV(RAND(probability), mean, standard_dev)进行各不确定性因素第1次随机模拟,采用式(2)计算风速带来的总不确定性程度分别为7.48%、8.12%和8.37%。再采用Excel中的What-If Analysis模拟工具进行模拟。
-
经过蒙特卡洛随机模拟后得到模拟值,对其进行参数统计,风速总不确定性程度平均值分别为7.82%、7.84%和7.86%;标准差分别为0.45%、0.53%和0.60%;95%置信区间风速不确定性程度分别为7.08~8.56、6.97~8.71、6.88~8.84。
据式(3)和式(4)计算风速总不确定性程度和风速引起的发电量不确定性程度,此处考虑风速-产量敏感因子1.80[18, 22]。采用同种机型,功率曲线带来的发电量不确定性程度为4.00%。发电量总不确定性程度由式(6)计算所得分别为13.36%~15.92%、13.17%~16.18%、13.01%~16.41%。具体结果如表3所示。
统计参数 标准差$ \sigma = 0.12\mu $ 标准差$ \sigma = 0.14\mu $ 标准差$ \sigma = 0.16\mu $ 模拟次数/次 2×104 2×104 2×104 平均值/% 7.82 7.84 7.86 标准差/% 0.45 0.53 0.60 中位数/% 7.81 7.81 7.87 95%置信区间风速不确定性/% 7.08~8.56 6.97~8.71 6.88~8.84 功率曲线引起的发电量不确定性程度/% 4.00 4.00 4.00 95%置信区间发电量总不确定性程度/% 13.36~15.92 13.17~16.18 13.01~16.41 Table 3. Statistics of Monte Carlo simulation and uncertainty of power generation
-
常规计算风速不确定性大小并不考虑不确定因素呈正态分布,而是直接赋予不确定性因素值。文章为了对比蒙特卡洛模拟法和直接赋予不确定因素值两种方法计算结果,在表2的平均值列按常规方法计算出了风速总不确定性程度为7.79%,风速带来的发电量不确定性程度为14.02%,再结合功率曲线带来的发电量不确定性程度为4.00%,则直接赋予不确定因素值带来的发电量总不确定性程度为14.58%。文章把折减和不确定性分开考虑,扣除折减后计算所得风场净发电量为130 GWh,风场发电量分布的标准差根据式(8)计算,再根据式(9)计算各概率下的超越发电量,此处因涉及的数据信息庞大,表4只列出了常用概率情况下的发电量,文章为方便书写,直接赋予不确定因素值方法计算相应的结果用表4中$ \sigma = 0 $表示。
发电量 标准差$ \sigma = 0 $ 标准差$ \sigma = 0.12\mu $ 标准差$ \sigma = 0.14\mu $ 标准差$ \sigma = 0.16\mu $ 年净发电量/GWh 130.00 130.00 130.00 130.00 P75 117.30 116.13~118.36 115.91~118.53 115.71~118.67 P84 111.24 109.51~112.81 109.18~113.05 108.88~113.26 P90 105.74 103.51~107.77 103.08~108.09 102.69~108.35 P95 98.92 96.06~101.52 95.50~101.92 95.01~102.26 P99 85.84 81.78~89.53 80.99~90.11 80.29~90.59 Table 4. Power generation with exceeding probability
-
文章针对此案例具体情况,对风场不确定性因素进行分类并确定其正态概率分布函数具体形式,标准差根据IEC设置了3种[21],文章将直接赋予不确定因素值计算结果纳入对比。
表2可以得出,蒙特卡洛进行第1次随机模拟风速总的不确定性程度分别为7.48%、8.12%、8.37%,与直接赋予不确定因素值计算结果7.79%分别相差−0.31%、0.33%、0.58%。
蒙特卡洛进行多次随机模拟结果是服从正态分布的具体函数,可以得到平均值和标准差及其它统计参数,表3中风速总不确定性程度平均值分别为7.82%、7.84%、7.86%;与直接赋予不确定因素值计算结果7.79%分别相差0.03%、0.05%、0.07%。随着模拟次数的增加,给定3种标准差的风速不确定性程度与直接赋予不确定因素值计算结果的差距变小。
表3模拟得到的风速总不确定性平均值和标准差,计算95%置信区间3种标准差风速不确定性总的大小区间分别为7.08%~8.56%、6.97%~8.71%、6.88%~8.84%,随着不确定性因素标准差的增加,不确定性程度的区间范围会以7.79%为概率分布的中心但跨度会变大。因发电量敏感因子的作用,95%置信区间发电量总不确定性程度分别为13.36%~15.92%、13.17%~16.18%、13.01%~16.41%,直接赋予不确定因素值带来的发电量总不确定性程度为14.58%。95%置信区间超越概率发电量分布范围为96.06~101.52 GWh、95.50~101.92 GWh、95.01~102.26 GWh。
表4所得风电场超越概率发电量,随着超越概率的增加,能保障的发电量变小;同一超越概率情况下,随着不确定性因素概率分布中标准差的增加,其超越概率发电量的区间范围跨度变大。
采用直接赋予不确定性因素值的计算方法能得到风速不确定性程度和超越概率发电量的平均值,但它忽略了不确定性因素是服从正态分布的概率函数,不能得到相应的超越概率发电量分布。
-
文章采用蒙特卡洛模拟法对引起风场发电量不确定性因素建模和程度进行模拟,不确定性因素建模遵循了其正态分布的本质,借助蒙特卡洛模拟法的优势可根据建立的模型生成随机样本,随着模拟次数的增加,其样本结果能代表总体结果。
蒙特卡洛模拟法模拟风场风速总不确定性程度,得到服从正态分布的具体函数,可以求出特定置信区间的风速不确定性程度的上下限,得出落在某一区间范围内的超越概率发电量,以此为依据计算风场收益和控制风险,将收益和风险进行量化对应,并将风险控制在一定范围内。
随着超越概率的增加,发电量会降低;同一超越概率情况下,随着不确定性因素标准差的增加,不确定性程度以及超越概率发电量的区间范围跨度会变大,风险会增加。
采用超越概率发电量作为依据评估风场投资风险,有助于决策建立在正确、可靠的基础上,明确不确定性因素的来源并在实际评估中去规避这些不确定性因素带来的风险。
Application of Monte Carlo Simulation for Calculating Power Generation with Exceeding Probability in Wind Farm
doi: 10.16516/j.ceec.2024.6.18
- Received Date: 2023-10-09
- Rev Recd Date: 2023-12-12
- Available Online: 2024-06-07
- Publish Date: 2024-11-30
-
Key words:
- uncertainty factors /
- normal distribution /
- Monte Carlo simulation method /
- wind speed-power generation sensitive factor /
- power generation with exceeding probability
Abstract:
| Citation: | LI Hua, ZHANG Binbin, DING Yanjun. Application of monte carlo simulation for calculating power generation with exceeding probability in wind farm [J]. Southern energy construction, 2024, 11(6): 174-182 doi: 10.16516/j.ceec.2024.6.18 |






 DownLoad:
DownLoad: