Analysis of Harmonic Instability of Tokamak Power System Caused by Rectifier Transformer Bias

对于Tokamak磁体电源系统，变流器负载多为数十毫亨至数亨量级的大电感，可以认为直流侧电流为平滑直线基本无脉动。考虑低频谐波计算的复杂性，首先忽略换相过程，采用调制函数法进行分析，而后对换相过程影响进行说明。假设并联运行时均流系数为1，每桥承担$ {I_{\text{d}}}/2 $。

设调制函数$f(t) = \varepsilon (t - {\alpha _{n}}) - \varepsilon (t - {\alpha _{n}} - {\alpha _{\text{v}}})$，由Fourier计算公式得：

式中：

$A = {\alpha _{\text{v}}}/2{\text{π}}$，${A_k} = 2\sin \dfrac{{k{\alpha _{\text{v}}}}}{2}/k{\text{π}}$，${\varphi _k} = k{\alpha _0} + \dfrac{{k{\alpha _{\text{v}}}}}{2}$；

$ {\alpha _{\text{v}}} $——晶闸管导通区间；

$ \alpha $ ——触发角；

$ {\alpha _0} $——导通时刻；

${\alpha _{n}}$——第n个晶闸管的触发时刻，当晶闸管导通时，调制函数取值为1，关闭时取值为0。

共阴极和共阳极的晶闸管按顺序依次导通120°，如图1所示。

Figure 1.  Thyristor conduction sequence modulation function

对于三相全控桥调制函数${\alpha _{\text{v}}} = \dfrac{2}{3}{\text{π}}$，${\alpha _{n}} = \dfrac{{(2n - 1){\text{π}} }}{6} + \alpha$，$ \alpha $相过零点为时间起点，将其代入式(1)可得：

A相交流电流是由调制函数$ {f_1} $、$ {f_4} $对直流电流$ {I_{\text{d}}} $调制的结果：

如图2所示三相全控桥并联运行，副边线电压差30°，两桥所产生的含量较高的5，7次谐波相位刚好相差180°，当幅值相等时，可以相互抵消。设$ {\stackrel{·}{U}}_{\text{A}1\text{B}1} $较$ {\stackrel{·}{U}}_{\text{A}2\text{B2}} $滞后30°，原副边绕组的电流瞬时值关系：

Figure 2.  Three phase fully controlled bridge parallel operation

故可推出：${i_{\text{A}}} = \displaystyle \sum\limits_{{k} = 1}^\infty \dfrac{{2\sqrt 3 }}{{k\text{π}}}{I_{\text{d}}} \cdot \sin k(\omega t - \alpha ), k = 12n \pm 1 。$

调制函数的影响，可以视为基本分量${s_{\text{n}}}$、修正分量${s_{\text{m}}}$和换相分量的叠加。基本分量${s_{\text{n}}}$、修正分量${s_{\text{m}}}$为幅值为1、宽度分别为$2{\text{π }}/3$和$\theta $的矩形波，前者反映不存在换相过程且严格按照触发脉冲导通的情况下变流器调制动作，后者则用于修正因变流器导通时刻偏移而引起的调制函数波形的变化^[12-13]。对应的电压电流开关函数为：

式中：

通过计算分析换相角对2次谐波影响小，为简化低次谐波建模，使模型具备工程实用价值，忽略换相不平衡造成的影响。

本节主要通过推导交流侧2次谐波与直流侧基频电流之间的关系，分析了ITER PF变流器建立直流偏磁等值参数电路，并得到整流变压器铁心饱和情况下谐波在变流器两侧以及整流变压器两侧的传递过程，如图3所示^[14-16]。

Figure 3.  Harmonic transmission diagram of rectifier transformer core saturation

结合图3中的2次谐波传递关系图可知，这是一个正反馈通道，即当线路中产生一个二次谐波扰动时，会经过上述正反馈通道进一步输出一个对应的二次谐波分量作用于变压器交流侧。对应的参数计算情况如下：

交直流系统电路对应的模型如图4所示。其中交流侧等值阻抗计算公式为：

Figure 4.  AC and DC circuit model

式中：

k ——变压器变比；

$ {Z_{\text{S}}} $ ——电源等值阻抗(Ω)；

$ {Z_{{\text{lb2}}}} $ ——滤波器和无功补偿装置的等值阻抗(Ω)；

${Z_{{\text{T2}}}}$ ——ITER变压器网侧对应的阻抗(Ω)。

参考ITER PF整流变压器参数（如表1所示），接入点等效阻抗根据主变接入点短路容量为922 MVA，故接入点的等效电抗为${X_{\text{S}}} = 14.348\;8\;\Omega $。根据$ {X_{\text{S}}} = 14.348\;8\;\Omega $可求出${R_{\text{S}}} = 1.434\;88\;\Omega $。

为了简化计算，采用“一”型等效电路，只考虑变压器的励磁支路和负载支路。对应的参数（66 kV侧）关系如下：

电阻${R_{\text{T}}} = \dfrac{{\Delta {P_{\text{k}}}{U_{{\text{1N}}}}^2}}{{{S_{{\text{TN}}}}^2}} = \dfrac{{423.92 \times {{66}^2}}}{{{{41\;000}^2}}} = 1.098\;5\;\Omega$，电抗${X_{\text{T}}} = \dfrac{{{U_{\text{k}}}\% }}{{100}} \times \dfrac{{{U_{\text{N}}}^2}}{{{S_{\text{N}}}}} = \dfrac{{15.63}}{{100}} \times 106.24 = 16.605\;3\;\Omega$，故对应变压器阻抗${Z_{\text{T}}} = {R_{\text{T}}} + j{X_{\text{T}}} = (1.098\;5 + 16.605\;3j)\Omega$。

ITER无功补偿及滤波系统测试平台安装容量168 Mvar，基波补偿容量83.2 Mvar，电压等级66 kV，等效电阻${R_{\text{L}}} = 0.131\;5\;\Omega $，滤波支路基波下的等效电抗为：

其它等效参数如表2所示。

相控电抗器为三角形连接，在实验过程中，由于容性滤波支路始终投入，那么随着负载电流的变化，TCR提供的补偿容量将在0～83.208 Mvar之间变化。计算过程中，将TCR等效为一个三相星形连接的可变电感，对应的基波等效阻抗${X_{{\rm{TCR}}}} = 52.350\;7\;\Omega \sim \infty$。

以ITER PF变流器集成试验的并联谐振等值回路进行分析，如图5所示。

Figure 5.  Parallel resonant equivalent circuit for ITER PF converter integration test

ITER PF变流器等效为谐波源，忽略主变压器励磁阻抗，等值电路进一步简化为图6所示电路。

Figure 6.  Simplified parallel resonant equivalent circuit of ITER pf converter

将相关等值参数折算到66 kV侧，得：${R_{\text{S}}}' = \dfrac{{1.434\;4 + 0.155\;8}}{{{{(115/66)}^2}}} = 0.523\;8\;\Omega$，${X_{\text{S}}}' = \dfrac{{14.343\;8 + 15.830\;3}}{{{{(115/66)}^2}}} = 9.938\;6\;\Omega$，${R_{{\text{TCR}}}} = 0.26\;\Omega$，$ {X_{{\text{TCR}}}} = $$52.350\;7\;\Omega$，${R_{\text{L}}} = 0.131\;5\;\Omega$，${X_{\text{C}}}' = 52.350\;7\;\Omega$，结合式(10)可以求解出$ {Z_{{\text{ac}}2}} $的值为：

根据表1主变参数的参数可知：触发角$\alpha = 15^\circ$，按网侧参数来折算，根据触发角$\alpha $和换相角$\mu $的关系，列出对应的关系如下：

式中：

${K_{\text{I}}}$ ——电容性元件对换相过程影响的修正系数，其取值主要受到特征次谐波的影响，考虑到此处分析的是二次谐波问题，故电容性元件对换相过程影响可忽略不计，所以${K_{\text{I}}} = 1$；

${I_{\text{d}}}$ ——网侧电流(A)；

${X_{\text{B}}}$ ——换相电抗(Ω)；

E ——网侧电压(kV)。

折算到66 kV侧，对应的各电抗值如下：

系统等效电抗${X_{\text{S}}} = 14.348\;8\;\Omega$，主变压器电抗${X_{\text{T}}} = 16.605\;3\;\Omega$，交流母排（包括封闭母线）${X_{{\text{bus}}}} = 1.489\;5\;\Omega$，所以换相电抗的大小为${X_{\text{B}}} = 32.443\;6\;\Omega$。

根据表1主变参数中数据可知：电压$E = 66\;{\text{kV}}$，${I_{\text{d}}} = 358.7\;{\text{A}}$。将相关值代入式(11)中可求解出μ的值。

图7所示为直流侧等值谐波阻抗的等值电路，其中${Z_{{\text{L}}(m)}}$、${Z_{{\text{E}}(m)}}$、${Z_{{\text{S}}(m)}}$分别为直流线路、对侧换流器的直流侧和平波电抗器的等值m次谐波阻抗(m为正整数)。

Figure 7.  DC side equivalent harmonic impedance circuit model

由图7可知：直流侧等值阻抗${Z_{{\text{dc}}1}} = {Z_{{\text{E}}1}} + 2{Z_{{\text{S}}1}} + {Z_{{\text{L}}1}}$。需要说明的是，由于超导电感非常大，可以认为${Z_{{\text{L}}1}} \gg {Z_{{\text{S}}1}}$，${Z_{{\text{L}}1}} \gg {Z_{{\text{E}}1}}$。设${L_1} = 1{\text{H}}$，从而得到直流侧阻抗${Z_{{\text{dc}}1}}$的值。

综合上述计算，对应的各参数值如表3所示。

结合图4可知：其会经过一正反馈通道输出一对应的二次谐波电压，该二次谐波电压为${\stackrel{·}{U}}_{{{\rm{ac}}2+}'}$对应的关系式为：

式中：

${I_{{\text{ac}}2}}$ ——二次谐波电流(A)；

${Z_{{\text{ac}}2}}$ ——交流侧二次谐波阻抗(Ω)；

$\mu $ ——换相角(°)；

k ——变压器变比；

${Z_{{\text{dc}}1}}$ ——直流侧阻抗(Ω)。

将表3中数值代入上式，整理可求出${\stackrel{·}{U}}_{{\text{ac}2}'}$。

设$\lambda $为换流变压器铁心饱和型谐波不稳定的稳定因子，当$\lambda > 1$时，扰动将随着时间增大而增大，系统出现不稳定；反之，即$0 < \lambda < 1$时，扰动会随着时间而衰减，系统最终趋于稳定。谐波电压$ {\stackrel{·}{U}}_{{\rm{ac}}2} $经变流器及饱和情况下的换流变压器在交直流两侧传变后，其对应的幅值增益$\lambda =\left|{\stackrel{·}{U}}_{{\text{ac}2}'}/{\stackrel{·}{U}}_{\text{ac2}}\right|=1.993\times {10}^{-10}$。这个结果几乎趋向于0，可以忽略不计。这说明，在ITER整流变压器系统中，因偏磁产生的扰动而导致的低次谐波可忽略不计。

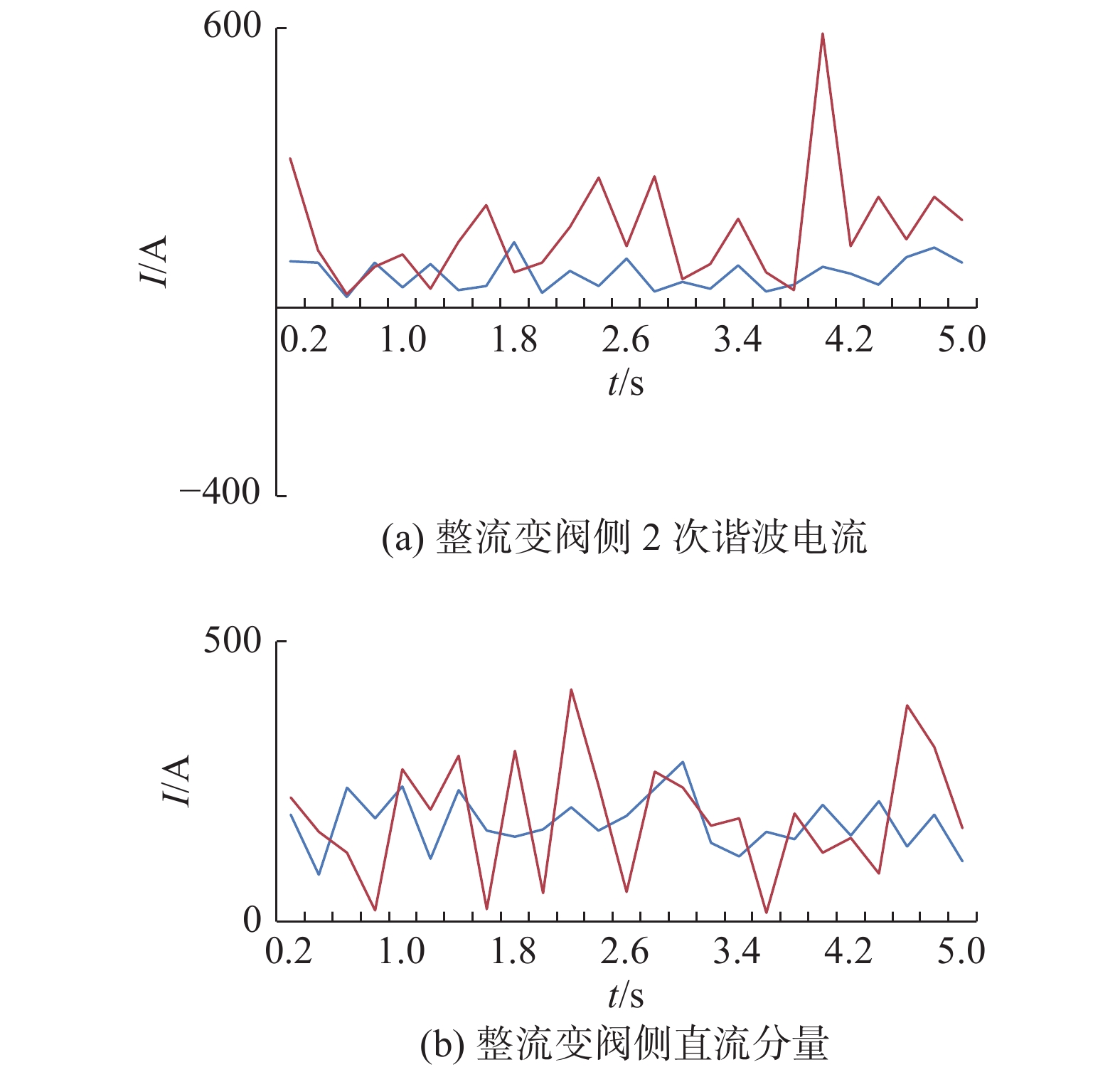
ITER PF变流器在合肥集成试验，1、3正向或2、4反向6脉波变流桥并联55 kA稳定运行时，整流变压器阀侧电流波形采用30 kA罗科和数据采集仪（20 kHz采样频率）采集，使用Origin软件进行FFT分析仿真，频谱分析时间窗按照IEC标准采用200 ms，2次谐波电流值和波动较大。图8(a)为1、3桥并联55 kA稳定运行，假负载2串2并（5 mH）时整流变阀侧2次谐波电流，图8(b)为同时刻检测到的直流分量，蓝色为1桥，红色为3桥。表4中列出1、3桥2次谐波电流和直流分量5 s的平均值。

Figure 8.  1、3 bridge second harmonic current component and DC current component

从图8可以看出1桥2次谐波电流最大达到近600 A且波动较大，3桥2次谐波电流最大仅为100 A且波动较小；可以看出1桥直流分量最大达到430 A且波动较大，3桥直流分量最大为280 A，波动相对较小。

图9(a)为2、4桥并联55 kA稳定运行，假负载2串2并（5 mH）时整流变阀侧2次谐波电流，图9(b)为同时刻检测到的直流分量，蓝色为2桥，红色为4桥。表5中列出2、4桥2次谐波电流和直流分量5 s的平均值。

Figure 9.  2、4 bridge second harmonic current component and DC current component

本文发展了一种改进型的开关函数，并基于这种改进型开关函数建立了ITER电源系统的数学模型，进而推导出整流变压器直流偏磁所产生的二次谐波输出。从实验结果来看，尽管整流变阀侧出现了百安培量级的直流分量，但其与整流变压器阀侧的数万A的比值小于对应的允许值0.033，不足以引起整流变直流偏磁，因此不存在由直流偏磁形成正反馈从而导致二次谐波的恶性循环。ITER PF变流器实际运行时负载为最大亨量级的超导大电感，直流侧不会发生工频串联谐振，可以排除直流偏磁引起的谐波不稳定。