-
随着新能源装机容量的不断提升,区域电网结构越发复杂,传统微电网由光伏、风电等高渗透率分布式电源点组成,具有低惯性、低阻尼的特性[1-2]。储能单元作为可以灵活充放电的电源,配置在微电网并网PCS直流侧,可以实现能量动态吸收、释放[3-4]。为了使储能微网具备同步发电机特性,为电网提供惯性和阻尼支撑,目前广泛采用VSG控制方法[5-7]。
传统VSG无法对系统提供暂态电压支撑,所以不具备LVRT能力。当网侧发生接地故障,造成系统电压对称或者不对称跌落事故时,储能微网设备极易脱网[8-10]。劳永钊[11]以网侧三相电压不平衡为研究对象,将新能源微网输出正序、负序电流进行解耦,分别提出相应并网冲击电流抑制方法。为了提高对LVRT期间的电流跟踪能力,季宇[12]将滑模观测器应用于储能PCS矢量电流环中,实现电流无差调节。王小辉[13]采用模型预测有限控制方法,根据光伏并网逆变器开关离散特性,不断优化增益开环特性,实现并网点电压支撑。秦晓辉[14]对阻尼系数进行改进,应用自适应阻尼在风机转子励磁控制系统中,可以有效抑制网侧电压骤升带来的转子电流震荡。涂娟[15]将VSG控制参数即虚拟惯量、阻尼系数与电压、电流闭环建立关系,选择合适的参数来抑制电压突降时候参数偏差。
本文针对储能微网LVRT电压暂态特性差问题,提出一种基于虚拟阻抗的储能微网VSG控制策略。首先建立储能微网PCS的VSG控制模型;然后引入虚拟阻抗到VSG无功-电压控制中,起到故障期间电压支撑作用;接着将LVRT工况分为储能外接输电线路对称和不对称接地故障,分析对应正序电压、电流,负序电压、电流,进而得到虚拟阻抗幅值及阻感比参数;最后通过仿真验证本文所提方案的有效性和可行性。
-
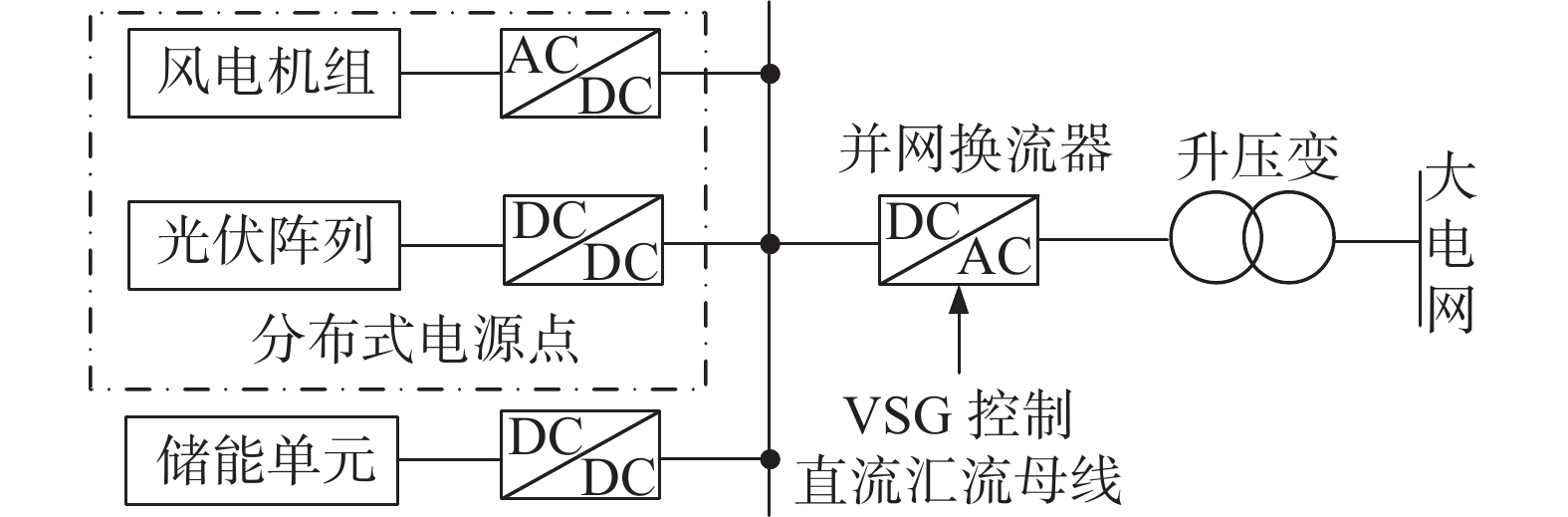
图1为含有分布式电源点及储能单元的微网拓扑图。光伏发电系统和风力发电系统构成分布式电源点,光伏阵列通过DC/DC换流器并入直流汇流母线,风电机组通过AC/DC换流器并入直流汇流母线。储能单元通过DC/DC换流器并入直流汇流母线,储能单元作为能量储存装置可以实现整个微网电能稳定外送/吸收。微网直流汇流母线通过DC/AC并网换流器及升压变与大电网相连。在DC/AC并网换流器中采用VSG控制策略,可以使储能微网具备旋转电动机惯性特性,为电网提供惯性和阻尼支撑。
建立储能微网PCS的LCL电路拓扑模型如图2。其中:Cdc为直流侧滤波电筒;Rf、Lf、Cf构成滤波电路;uabc、iabc为PCS交流三相桥臂电压、电流;eabc为PCS并网点三相电压;Lg、Rg构成线路阻抗。
以储能微网向交流主网功率传输方向为正,储能微网PCS输出有功、无功功率为:
$$ \left\{ \begin{gathered} P = \dfrac{E}{{R_{\text{g}}^2 + X_{\text{g}}^2}}\left( {{R_{\text{g}}}U\cos \delta + {X_{\text{g}}}U\sin \delta - {R_{\text{g}}}E} \right) \\ Q = \dfrac{E}{{R_{\text{f}}^2 + X_{\text{g}}^2}}\left( { - {R_{\text{g}}}U\sin \delta + {X_{\text{g}}}U\cos \delta - {X_{\text{g}}}E} \right) \\ \end{gathered} \right. $$ (1) 式中:
Xg ——线路电感Lg对应的感抗(mH);
U ——PCS交流三相桥臂电压幅值(V);
E ——PCS并网点三相电压幅值(V);
δ ——功角(°)。
输电线路成主感性,即感抗远大于阻抗(Xg>Rg)。储能微网并网情况下,PCS输出电压与网侧电压无相角差(δ≈0°),则有:sinδ≈δ,cosδ≈0。
储能微网PCS输出有功、无功功率简化为:
$$ \left\{ \begin{gathered} P = \dfrac{{EU}}{{{X_{\text{g}}}}}\delta \\ Q = - \dfrac{{{E^2}}}{{{X_{\text{g}}}}} \\ \end{gathered} \right. $$ (2) 根据式(2)可知:储能微网PCS输出有功功率与功角存在线性关系,无功功率与储能微网PCS并网点电压幅值呈线性关系,基于此,可以实现功率解耦控制。
-
本文在储能微网PCS控制系统中,采用VSG控制策略,图3为储能微网PCS的VSG控制框图。
图3中:Pe、Qe分别为储能微网PCS有功、无功功率实际输出值;Pref、Qref分别为有功、无功功率目标值;θ、ω分别为VSG虚拟电角度、虚拟电角速度,存在
${\rm{d}}\theta /{\rm{d}}t = \omega $ ;uV为VSG虚拟内电势。储能PCS的VSG转子机械方程为:
$$ J\dfrac{{{\rm{d}}\omega }}{{{\rm{d}}t}} = {T_{\text{m}}} - {T_{\text{e}}} - {T_{\text{d}}} = \frac{1}{\omega }\left( {{P_{{\text{ref}}}} - {P_{\text{e}}}} \right) - D\left( {\omega - {\omega _0}} \right) $$ (3) 式中:
J、D ——VSG虚拟转动惯量、阻尼系数;
Tm、Te、Td ——机械转矩、电磁转矩及阻尼转矩(N·m);
ω0 ——额定虚拟角速度(rad/s)。
VSG有功功率本质是在有功-频率下垂控制基础上引入虚拟转动惯量J具备同步发电机的旋转惯性。同时引入阻尼系数D来抑制电网功率调节过程中的振荡现象。
VSG同样可以模拟同步发电机励磁电流控制方式实现电压幅值调节,具备励磁调节惯性。类比于储能PCS的VSG转子机械方程,可以得到无功-电压调节方程为:
$$ {K_{\rm{u}}}\frac{{{\rm{d}}\Delta U}}{{{\rm{d}}t}} = \left( {{Q_{{\text{ref}}}} - {Q_{\text{e}}}} \right){\text{ + }}{K_Q}\left( {{u_{\rm{d}}} - {u_{{\text{V}}{\rm{d}}}}} \right) $$ (4) 式中:
Ku ——无功等效惯性系数;
ΔU ——电无功-电压调节量(V);
KQ ——无功-电压调节系数;
ud ——dq坐标系下d轴PCS桥臂电压有效值(V);
uVd ——dq坐标系下d轴VSG虚拟内电势(V)。
-
根据图2储能微网PCS的LCL电路拓扑图,基于基尔霍夫电压定律可得:
$$ L\frac{{{\rm{d}}{i_{{\text{abc}}}}}}{{{\rm{d}}t}} = {u_{{\text{abc}}}} - {i_{{\text{abc}}}}R - {e_{{\text{abc}}}} $$ (5) 式中:
L ——等效电感(mH),L=Lf+Lg;
R ——等效电阻(Ω),R=Rf+Rg。
定义Tabc→dq0为Park变换矩阵,则储能微网PCS交流三相桥臂电压、电流、并网点三相电压可转换为:
$$ \left\{ \begin{gathered} {\left[ {{u_{\rm{d}}}\;{u_{\rm{q}}}} \right]^{\text{T}}} = {T_{{\text{abc}} \to {\rm{dq}}{\text{0}}}}{\left[ {{u_{\text{a}}}\;{u_{\text{b}}}\;{u_{\text{c}}}} \right]^{\text{T}}} \\ {\left[ {{i_{\rm{d}}}\;{i_{\rm{q}}}} \right]^{\text{T}}} = {T_{{\text{abc}} \to {\rm{dq}}{\text{0}}}}{\left[ {{i_{\text{a}}}\;{i_{\text{b}}}\;{i_{\text{c}}}} \right]^{\text{T}}} \\ {\left[ {{e_{\rm{d}}}\;{e_{\rm{q}}}} \right]^{\text{T}}} = {T_{{\text{abc}} \to {\rm{dq}}{\text{0}}}}{\left[ {{e_{\text{a}}}\;{e_{\text{b}}}\;{e_{\text{c}}}} \right]^{\text{T}}} \\ \end{gathered} \right. $$ (6) 将式(6)带入式(5),可以得到储能微网PCS在dq两相坐标系下的数学模型为:
$$ \left\{ \begin{gathered} {u_{\rm{d}}} = {e_{\rm{d}}} + L\dfrac{{{\rm{d}}{i_{\rm{d}}}}}{{{\rm{d}}t}} + {i_{\rm{d}}}R - \omega L{i_{\rm{q}}} \\ {u_{\rm{q}}} = {e_{\rm{q}}} + L\dfrac{{{\rm{d}}{i_{\rm{q}}}}}{{{\rm{d}}t}} + {i_{\rm{q}}}R + \omega L{i_{\rm{d}}} \\ \end{gathered} \right. $$ (7) 电流闭环调节采用PI控制方式,传递函数为:
$$ \left\{ \begin{gathered} {u_{\rm{d}}} = \left( {{K_{\text{P}}} + \dfrac{{{K_{\text{I}}}}}{s}} \right)\left( {i_{\rm{d}}^* - {i_{\rm{d}}}} \right) - \omega L{i_{\rm{q}}} + {e_{\rm{d}}} \\ {u_{\rm{q}}} = \left( {{K_{\text{P}}} + \dfrac{{{K_{\text{I}}}}}{s}} \right)\left( {i_{\rm{q}}^ * - {i_{\rm{q}}}} \right) - \omega L{i_{\rm{d}}} + {e_{\rm{q}}} \\ \end{gathered} \right. $$ (8) 式中:
Kp、KI ——电流闭环PI调节控制中比例调节系数、积分调节系数;
id*、iq* ——对应电流参考值(A)。
-
储能微网PCS的VSG控制系统正常工作时,PCS输出电压实时跟踪网侧电压。当网侧发生对侧短路或者不对称短路时,即单相、两相或三相短路接地故障,外接线路阻抗降低,电压大幅下跌,储能微网PCS并网点电压变化量为:
$$ \left\{ \begin{gathered} \Delta {u_{\rm{d}}} = {u_{\rm{d}}} - u_{\rm{d}}^ * \\ \Delta {u_{\rm{q}}} = {u_{\rm{q}}} - u_{\rm{q}}^ * \\ \end{gathered} \right. $$ (9) 式中:
ud*、uq*——发生短路时,ud、uq电压目标值(V)。
本文采用虚拟阻抗来补偿Δud、Δuq,增加储能PCS的VSG控制系统LVRT能力,虚拟阻抗构造为:
$$ {Z_{{\rm{X}}}}\left( s \right) = - {R_{{\rm{X}}}} + s{L_{{\rm{X}}}} $$ (10) 式中:
RX ——虚拟电阻(Ω);
LX ——虚拟电感(mH)。
dq坐标系下,ZX补偿压降为:
$$ \left\{ \begin{gathered} \Delta {u_{\rm{d}}} = {L_{{\rm{X}}}}\frac{{{{\rm{d}}}{i_{\rm{d}}}}}{{{\rm{d}}t}} + {R_{{\rm{X}}}}{i_{\rm{d}}} - \omega {L_{{\rm{X}}}}{i_{\rm{q}}} \\ \Delta {u_{\rm{q}}} = {L_{{\rm{X}}}}\frac{{{{\rm{d}}}{i_{\rm{q}}}}}{{{\rm{d}}t}} + {R_{{\rm{X}}}}{i_{\rm{q}}} + \omega {L_{{\rm{X}}}}{i_{\rm{d}}} \\ \end{gathered} \right. $$ (11) 将虚拟阻抗ZX补偿压降带入储能微网PCS的VSG无功-电压调节方程中,可得:
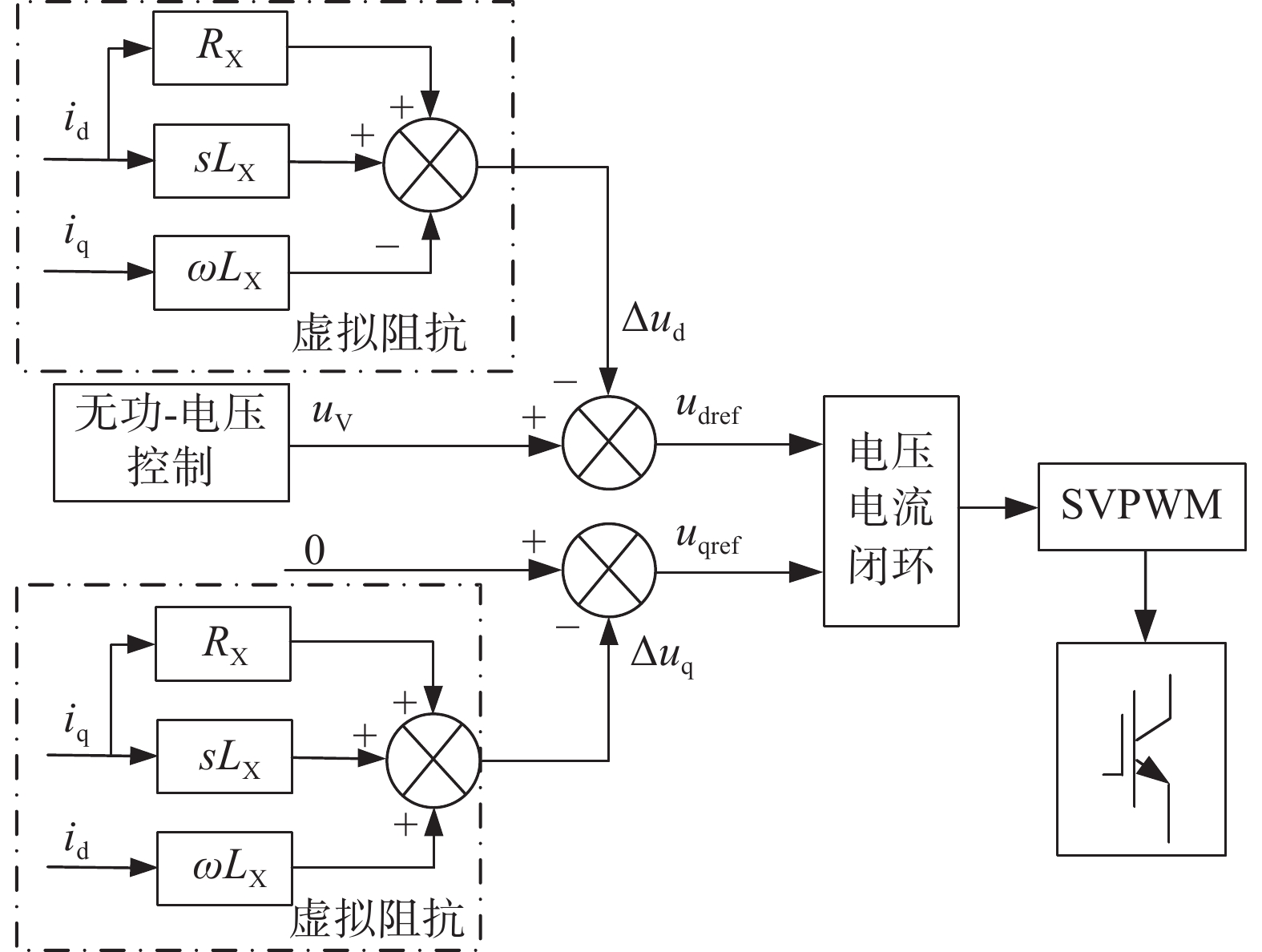
$$ {K_{\rm{u}}}\frac{{{\rm{d}}\Delta U}}{{{\rm{d}}t}} = \left( {{Q_{{\text{ref}}}} - {Q_{\text{e}}}} \right){\text{ + }}{K_Q}\left[ {{u_{\rm{d}}} - \left( {{u_{{\text{V}}{\rm{d}}}} - \Delta {u_{\rm{d}}}} \right)} \right] $$ (12) 加入虚拟阻抗后储能微网PCS的VSG无功-电压调节控制框图如图4所示。

Figure 4. VSG reactive power-voltage control block diagram of PCS for energy storage microgrid with virtual impedance
虚拟阻抗本质是在电压控制引入电流反馈环节,用输出电流在虚拟阻抗上的压降不断矫正电压目标值,提高暂态电压,从而起到当网侧发生对侧短路或者不对称短路时,电压支撑作用,提高储能PCS的VSG控制系统LVRT能力。
-
电网接地故障可分为对称短路和不对称短路。对称短路即三相接地短路,故障网络对称,此时储能微网PCS输出电压只存在正序分量;不对称短路可分单相接地和两相接地短路,对称电流通过故障线路导致储能微网PCS输出电压不对称,若储能微网采用中性点不接地方式,则此时输出电压不仅存在正序分量还存在负序分量。将储能微网等效为恒压源,短路等效电路如图5所示。
图5中:uf1、uf2为正序、负序电压;if1、if2为正序、负序电流;C为并联电容器。正序电流表示为:
${i_{{\text{f1}}}} = \dfrac{{u - {u_{{\text{f1}}}}}}{{{Z_{{\rm{X}}}}}}$ ;负序电流表示为:${i_{{\text{f2}}}} = \dfrac{{{u_{{\text{f2}}}}}}{{{Z_{{\rm{X}}}}}}$ 。当发生不对称短路时,储能微网外接输电线路同时存在if1、if2,储能微网PCS的VSG控制系统中id、iq除了存在直流分量正序电流外,还叠加了负序二倍振荡分量,可表示为:
$$ \left\{ \begin{gathered} {i_{\rm{d}}} = {I_{{\text{f1}}}} + {I_{{\text{f2}}}}\cos \left( {2\omega t} \right) \\ {i_{\rm{q}}} = {I_{{\text{f2}}}}\cos \left( {2\omega t} \right) \\ \end{gathered} \right. $$ (13) 式中:
If1、If2——正序、负序电流if1、if2的幅值(A)。
根据正序、负序电流表达式及式(13)可以得到虚拟阻抗ZX幅值为:
$$ \left| {{Z_{{\rm{X}}}}} \right| = \frac{{\left| {u - {u_{{\text{f1}}}}} \right| + \left| {{u_{{\text{f2}}}}} \right|}}{{{I_{\lim }}}} $$ (14) 式中:
Ilim——电流矢量限幅半径(A),短路情况下对任意相电流起到限值作用,避免短路电流超过矢量限幅圆。
正序、负序电流幅值满足:
$$ {I_{\lim }} \geqslant {I_{{\text{f1}}}} + {I_{{\text{f2}}}} $$ (15) -
当发生对称短路故障时,由于不存在负序分量,根据图5中正序模型,可以得到储能微网等效故障网络如图6所示。
图6中:Zg1为储能微网外接输电电路短路点到PCS并网点线路阻抗;uF为故障点对地压降。
根据图6可以得出当发生对称短路故障时,储能微网PCS输出电压可表示为:
$$ u = {u_{\text{F}}}{\text{ + }}\left( {{Z_{{\rm{X}}}} + {Z_{{\text{g1}}}}} \right){i_{{\text{f1}}}} $$ (16) 为了实现在发生对称短路故障时,储能微网PCS的VSG控制系统电压支撑,需要正序电流保持最大,此时if1=Ilim,ZX阻感比为1,虚拟电阻RX、虚拟电感LX存在以下关系:
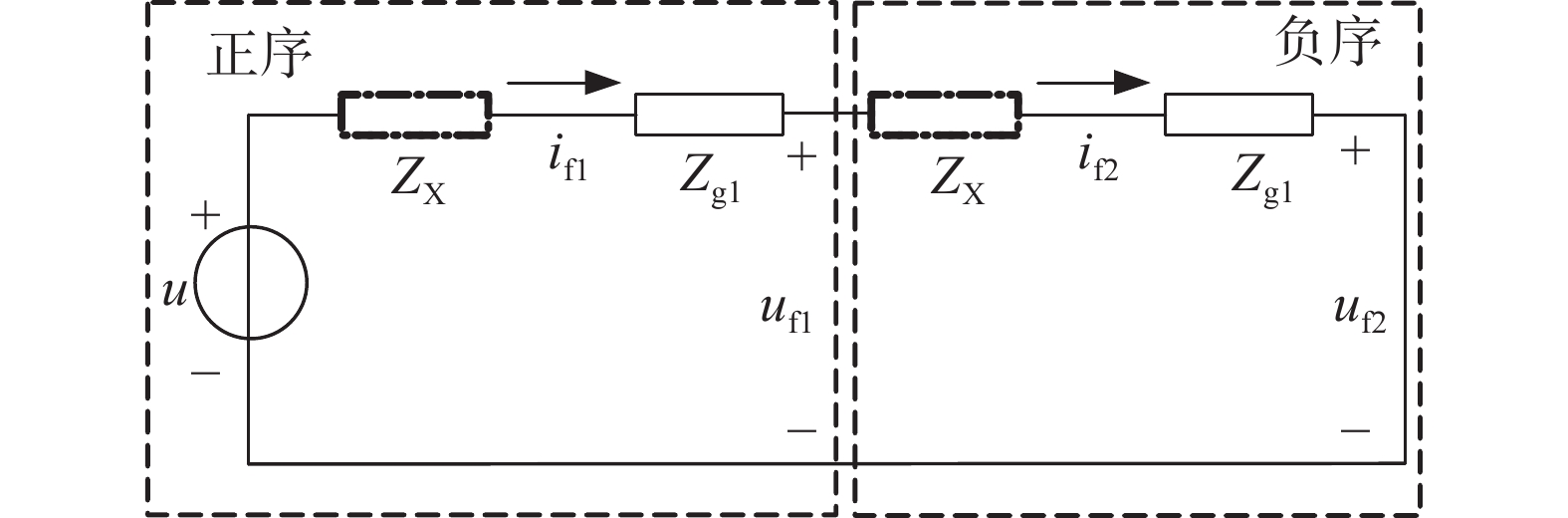
$$ \dfrac{{\left| {{R_{{\rm{X}}}}} \right|}}{{\left| {{L_{{\rm{X}}}}} \right|}} = 1 $$ (17) 当发生不对称短路,储能微网等效故障网络同时存在图5中正序模型、负序模型,如图7所示。
图7中:正、负序阻抗相等,故障点线路阻抗相等,此时正序电流if1与负序电流if2相等。储能微网PCS输出电压可表示为:
$$ u = {u_{{\text{f1}}}}\dfrac{{2\left( {{Z_{{\text{g}}1}} + {Z_{\text{X}}}} \right)}}{{2{Z_{{\text{g}}1}} + {Z_{\text{X}}}}}{\text{ = }}{u_{{\text{f2}}}}\dfrac{{2\left( {{Z_{{\text{g}}1}} + {Z_{\text{X}}}} \right)}}{{{Z_{\text{X}}}}} $$ (18) 从式(18)可以看出:if1、if2与Zg1、Zx成线性关系。为了抑制不对称短路造成的电压不平衡,使控制系统具备电压支撑能力,当发生不对称短路时,设置虚拟阻抗阻感比与故障点线路阻抗阻感比相同,即:
$$ \dfrac{{\left| {{R_{X}}} \right|}}{{\left| {{L_{X}}} \right|}}{\text{ = }}\dfrac{{\left| {{R_{{\text{g1}}}}} \right|}}{{\left| {{L_{{\text{g1}}}}} \right|}} $$ (19) -
为了验证本文所提方案可行性。在Matlab/Simulink仿真平台下搭建如图1所示储能微电网模型。储能微电网中:风电系统参数如表1所示;光伏系统参数如表2所示;储能系统参数如表3所示;储能微网PCS仿真参数如表4所示;储能微网外接输电线路参数如表5所示。
参数 数值 参数 数值 额定功率 0.3 WM 额定直流电压 510 V 额定转速 1 800 r/min 极对数 2 定子电阻 0.62 Ω 转子电阻 0.64 Ω 定子电抗 0.004 Ω 转子电抗 0.004 Ω Table 1. Simulation parameters of wind power system
参数 数值 参数 数值 额定功率 0.2 WM 额定直流电压 510 V 最大功率电流 22.8 kA 换流器容量 250 kVA Table 2. Photovoltaic system parameters
参数 数值 参数 数值 额定容量 50 kVA 额定直流电压 510 V 蓄电池充电极限 95% 蓄电池放电极限 25% Table 3. Parameters of energy storage system
参数 数值 参数 数值 直流母线电压 530 V 交流线电压 380 V 开关频率 10 kHz 额定角频率 314 rad/s 滤波电感 1 mH 滤波电容 4 700 μF Table 4. Simulation parameters of PCS for energy storage microgrid
参数 数值 参数 数值 线路长度 20 km 单位电阻 0.122 Ω/km 单位电感 0.931 mH/km 单位电容 12.73 μF/km Table 5. Parameters of external transmission line of energy storage microgrid
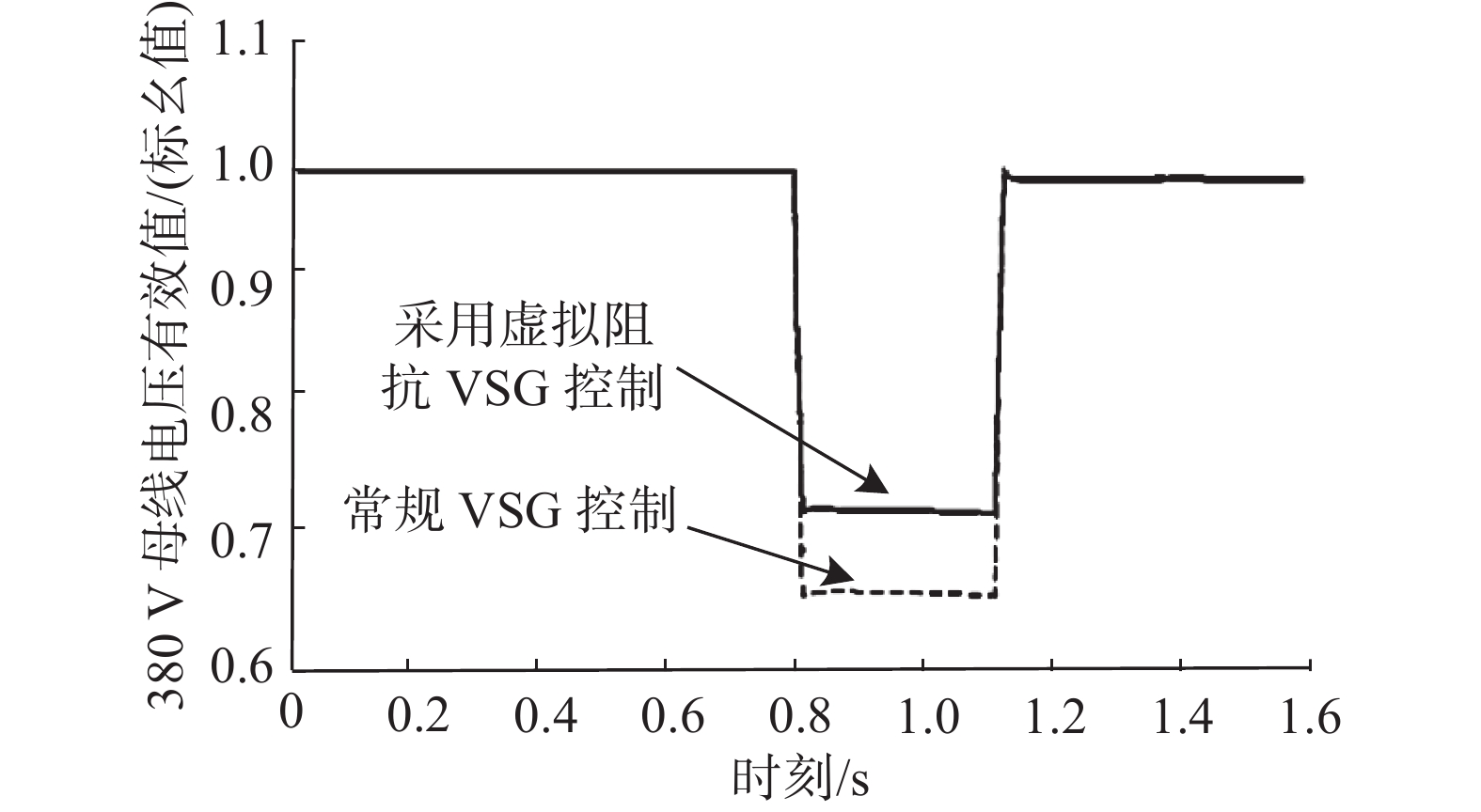
为了验证本文所提基于虚拟阻抗的储能微网VSG控制策略可以有效提高当外送线路侧短路时候的LVRT能力,本文设置仿真工况为0.8 s线路发生对称短路(三相接地)、不对称短路(单相接地),1.16 s继电保护动作切除故障。采用常规VSG控制和虚拟阻抗VSG控制对比波形如图8、图9所示。
根据图8可知:当0.8 s线路发生对称短路,常规VSG控制和虚拟阻抗VSG控制都可以响应电压暂态下降,在0.8~1.16 s之间,虚拟阻抗VSG控制因为虚拟阻抗电压提升明显,可以有效提高储能微网PCS输出电压,起到LVRT期间电压暂态支撑作用,相较于传统VSG控制,储能微网PCS输出电压提升0.12 p.u.,避免了对电压下降敏感用电设备低电压保护动作,使储能微网具备LVRT能力。
根据图9可知:当0.8 s线路发生不对称短路,相较于对称短路,母线电压下降较少,常规VSG控制和虚拟阻抗VSG控制都可以响应电压暂态下降,在0.8~1.16 s之间,虚拟阻抗VSG控制暂态电压相较于传统VSG控制提升0.06 p.u.,1.16 s继电保护动作切除故障后,也可迅速恢复至额定电压,采用虚拟阻抗的VSG控制系统具备LVRT能力。
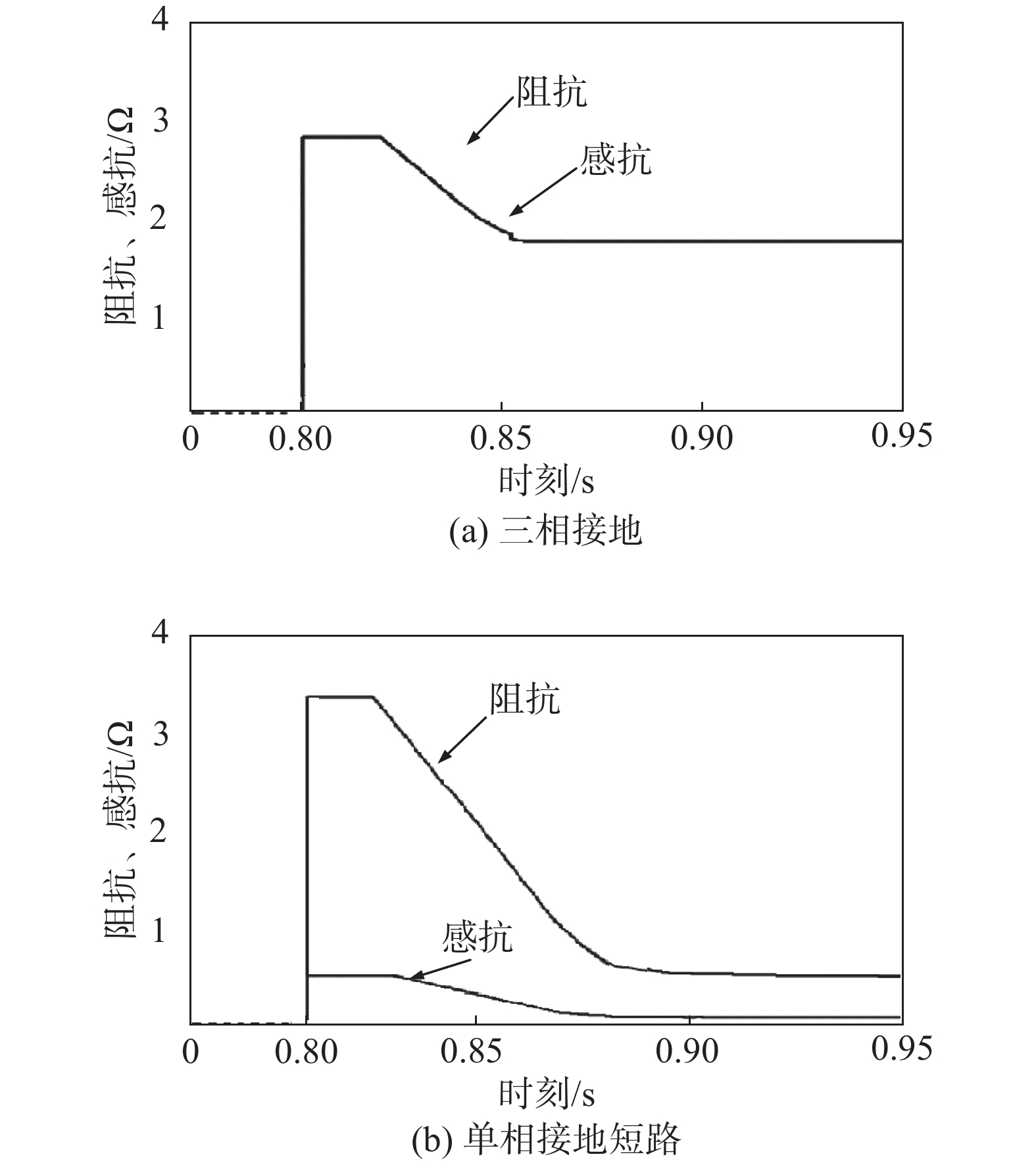
图10为0.8 s时刻,线路发生三相接地、单相接地故障时,虚拟阻抗介入后,虚拟阻抗的阻抗、感抗变化情况对比图。
从图10(a)可以看出:当发生三相接地故障时,虚拟阻抗介入后呈线性递减状态,此时虚拟阻抗阻感比始终保持在1,虚拟电阻与虚拟电抗幅值始终保持相等且始终与目标电压相匹配,起到电压支撑的作用。从图10(b)可以看出:当发生单相接地短路故障时,控制系统动态调节虚拟阻抗,虚拟阻抗阻感比与线路阻抗阻感比相同,并呈线性递减,起到最大支撑故障电压作用。
-
本文提出一种储能微网PCS采用VSG控制策略。针对传统VSG不具备LVRT能力,引入虚拟阻抗到VSG无功-电压控制中。将LVRT工况分为网侧对称和不对称短路故障,为了得到虚拟阻抗的幅值及阻感比,将LVRT工况分为线路对称和不对称短路障,研究正、负序电压、电流,最终得到虚拟阻抗的虚拟阻抗幅值及阻感比。
通过Matlab/Simulink仿真果表明:本文将虚拟阻抗引入VSG控制系统中,可以提高短路情况下储能微网PCS输出电压,起到LVRT期间电压暂态支撑作用,使储能微网VSG控制系统具备LVRT能力。具有一定的工程应用价值。
Research on VSG Control Strategy for Energy Storage Microgrid Based on Virtual Impedance
doi: 10.16516/j.gedi.issn2095-8676.2022.S2.015
- Received Date: 2022-02-25
- Rev Recd Date: 2022-06-07
- Available Online: 2023-01-04
- Publish Date: 2023-01-04
-
Key words:
- energy storage microgrid /
- virtual synchronous generator /
- low voltage ride through capability /
- virtual impedance /
- reactive power - voltage control
Abstract:
| Citation: | XIE Nan, YANG Peihao, HE Ping, CHEN Yao. Research on VSG Control Strategy for Energy Storage Microgrid Based on Virtual Impedance[J]. SOUTHERN ENERGY CONSTRUCTION, 2022, 9(S2): 90-97. doi: 10.16516/j.gedi.issn2095-8676.2022.S2.015 |





































 DownLoad:
DownLoad: