Extraction Method of Offshore Wind Power Output Characteristic Curve Based on Gaussian Mixture Model and Its Application in Electric Quantity Balance

当前，能源转型变革正在全球兴起，新能源替代传统化石能源，电能在能源消费中比例提升是全球能源格局发展的大势所趋，世界各国也都面临着巨大的挑战^[1]。我国海岸线长达1.8万km，大小岛屿有6 000余座，可利用海域面积300多万km²，拥有发展海上风电的天然优势。与陆上风电相比，海上风电具有不占用土地、风速高、风电机组发电量大、离负荷中心近、易消纳等优势。然而，海上风电存在间歇性强、波动性大、双向调峰性的特性，在碳达峰、碳中和背景下未来大规模海上风电并网无疑将对电网的电量平衡提出更高的挑战。因此，为了更准确地掌握海上风电大规模并网对于电网电量平衡的影响、合理开发海上风电与进行电网配套建设，对海上风电出力曲线进行更合理和细致地分类与提取，具有十分重要的意义。

目前，海上风电出力曲线的研究普遍采用的方法是基于各风电场出力的原始曲线，通过聚类分析的方法对实际风电出力场景进行提取、归类和简化。国内外对包含风电在内的新能源发电出力特性做了大量研究。为研究风电典型场景下的出力分布特征，相关研究采用最优核函数带宽选择的改进型非参数核密度估计法^[2]、采用贝塔（Beta）分布拟合风电出力的预测误差^[3-5]、采用流体计算模型，提出基于风资源评估不确定分析方法的风电有效出力计算模型^[6]等不同模型对风电出力进行拟合。

通过不同算法、模型分别得到风电出力特征，进一步归纳得到风电典型场景集，对提出具备实际应用场景的风电出力模型有较大意义。文献[7]基于改进k-means聚类算法，得到风电功率典型场景并将场景应用到电力系统日前调度；文献[8-9]通过k-means聚类实现对风电场出力样本的聚类划分，得到典型风电场出力场景并将场景应用到电力系统日前调度；以上场景提取均受限于k-means聚类数的选取而对聚类结果有不利影响。文献[10]基于Wasserstein概率距离指标和改进k-medoids对原始风电出力数据进行划分，得到经典风电场出力场景集；文献[11]通过分层聚类法和主成分分析法对风电出力历史数据进行处理，提取出典型风电出力场景；文献[12]分别采用改进k-means聚类和两步聚类算法得到风电的典型场景集；文献[13]基于概率分布的高斯混合聚类模型GMM(Gaussian Mixture Model)，以某一类的概率大小为样本相似度判断，对风电出力场景划分，获得风电的典型场景集；以上研究缺少基于不同海风区域和不同出力特性情况进行分类和特征曲线的提取，这样就导致无法反映出不同海风区域海上风电出力的特性，因而无法更好地反应各海风区域的特征。另外，由于无法针对不同出力特性的海风曲线给出不同类别的特征曲线，因而使得利用海风曲线进行的电量平衡计算结果失准。

因此，本文提出一种基于贝叶斯信息准则BIC(Bayesian Information Criterion)的高斯混合聚类模型GMM，对各海风区域出力的原始曲线进行分类，形成不同特征的曲线簇，并在各类曲线簇的基础上，按照时间特征使用箱型图对原始数据进行筛选并提取特征值，迭代筛选后每一类各得到一条代表性曲线，作为此类海上风电曲线簇的日出力特征曲线，用于海上风电出力的电量平衡计算。

根据区域海上风电分布情况和基于海上测风塔8 760 h测风数据，结合海域位置、离岸距离以及风速情况，将全区域海上风电划分为N个风区。

结合子区域内各风区海上风电规模和各风区小时级海上风电出力原始曲线，通过加权求和的方式可以得到子区域的小时级海上风电出力原始曲线，公式如下：

式中：

A_it ——当前区域的小时级海上风电出力原始曲线；

i ——风区；

m ——当前区域内的风区的总数目；

P_it ——风区i的海上风电出力原始曲线(t=$1, 2,\cdots,8\;760 $)；

α_i ——风区i的海上风电规模占当前区域的海上风电总规模的比重。

对全域内所有分风区内海上风电场出力序列进行叠加，可得到全域海上风电出力曲线。

GMM是一种基于概率模型的聚类方法，GMM假设输入样本服从k个参数未知的高斯分布，服从同一分布的样本则被聚为一类。GMM利用最大期望(Expectation-Maximization, EM)算法对k个混合的高斯分布进行拟合，以求得每个分布的均值和协方差。相较于应用广泛的k-means聚类、层次凝聚聚类等方法，GMM聚类方法在复杂分布能够获得较好的拟合效果，且聚类效果优于k-means^[14-15]。

假设一天内每个小时的风电功率$ {x_i} $(i=$1,2,\cdots , 24 $)，则高斯混合模型可以表示为：

式中：

$ x $ ——随机变量；

$ p(x) $ ——随机变量$ x $的概率；

${{\text{π}} _k}$ ——权重系数，且满足$\sum\nolimits_{k = 1}^K {{{\text{π}} _k} = 1}$；

$ N(x\left| {{\mu _k},{\varepsilon _k}} \right.) $ ——混合模型中的第k个高斯分布分量。

以上高斯混合模型有3个参数需要估计，分别为均值$ {\mu _k} $、权重系数${{\text{π}} _k}$${\text{π}}$以及方差$ {\varepsilon _k} $。

上式也可以转化为：

下面采用最大期望算法(EM)进行以上参数估计。算法具体步骤如下：

1）指定$ \mu $，${\text{π}}$，$ \varepsilon $的初始值。

2）计算后验概率$ \gamma (k) $：

3）求解$ {\mu _k} $的最大似然函数：

4）求$ {\varepsilon _k} $的最大似然值：

5）求解${{\text{π}} _k}$的最大似然函数：

6）如果满足$ \left\| {{\mu ^{(k)}} - {\mu ^{(k - 1)}} < {\alpha _1}} \right\| $、$\left\| {{\varepsilon ^{(k)}} - {\varepsilon ^{(k - 1)}} < {\alpha _2}} \right\|$和$\left\| {{{\text{π}} ^{(k)}} - {{\text{π}} ^{(k - 1)}} < {\alpha _3}} \right\|$（其中$ {\alpha _1} $、$ {\alpha _2} $和$ {\alpha _3} $为收敛判断阈值），则$ \mu $，${\text{π}}$，$ \varepsilon $的值分别取$ {\mu ^{(k)}} $，$ {\varepsilon ^{(k)}} $，${{\text{π}} ^{(k)}}$；否则循环计算步骤2)~步骤6)，直至算法收敛。

对于最佳聚类个数的确定，GMM聚类往往是采用BIC^[16]。BIC是在1978年由Schwarz提出，用于实际中选择最优的模型。本文利用基于BIC的模型选择理论对GMM的分组个数进行概率估计，通过逼近的方式逐步获得最优聚类数目。BIC的定义如下式所示：

式中：

k ——模型参数个数；

n ——样本数量；

L ——估计模型似然函数最大值；

kln(n) ——惩罚项，在维数过大且训练样本数据相对较少的情况下，可以有效避免出现维度灾难现象。

假设模型的误差或扰动呈正态分布，则BIC可表示为：

式中：

${S_{{\rm{RSS}}}}$——估计模型的残差平方和。

BIC是$ {S_{{\rm{RSS}}}} $和k的递增函数，即残差和未知参数的引入会使BIC增大。因此，在判断海上风电出力最优聚类个数时，以具有低BIC值的模型为优。

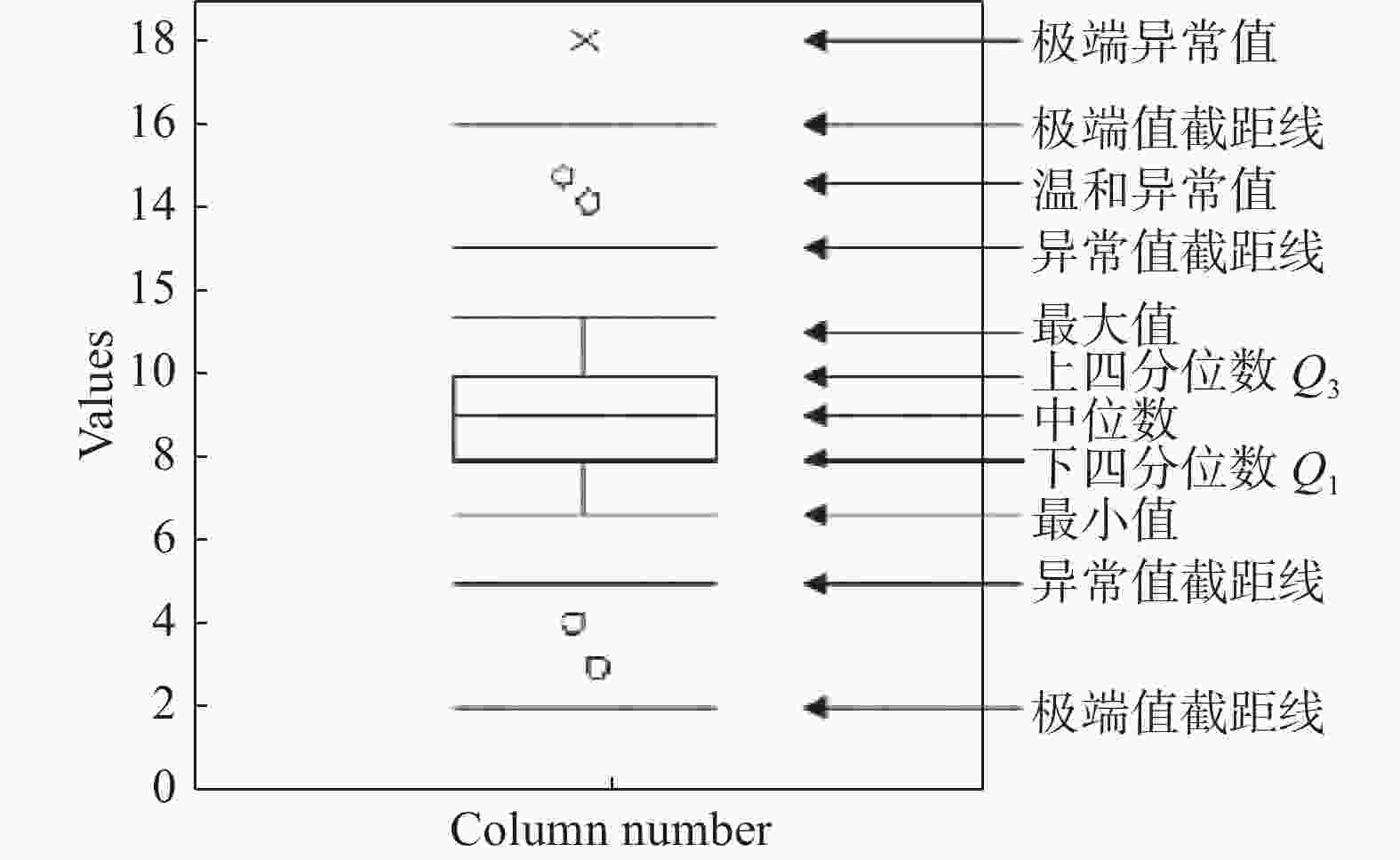
箱型图也叫箱线图，是检验样本数据中异常值的常用方法。箱型图上下为样本最大值和最小值，样本中位数置于箱型图中部，四分位数的间距为箱长（IQR），中位数上下端为上四分位数（Q₃）和下四分位数（Q₁）。箱形图的结构如图1所示。

Figure 1.  Box plot′s structure

当样本数据不在[Q₃-1.5IQR，Q₃+1.5IQR]区间时，定义为箱型图的异常值。本文对异常值采用剔除的方法进行处理，以保证结果的可靠性，经筛选后的曲线能真实直观地表现出力曲线原始特性。

针对不同风电场、不同海风区域和不同特性的海风出力曲线，通过不同海风区域的划分，建立各海风区域出力的原始曲线，在挑出夏季反调峰特性曲线的基础上，对剩余出力曲线根据其出力特性、波动趋势等特征，采用GMM对原始曲线进行分类，形成不同特征的曲线簇。在各类曲线簇的基础上，按照时间特征使用箱型图对原始数据进行筛选并提取特征值，迭代筛选后每一类各得到一条代表性曲线，作为此类海上风电曲线簇的日出力特征曲线。对各类日出力特征曲线的月度分布特性进行统计分析，在此基础上拟定不同海上风电出力情景，并得到各情景的概率值，具体分类步骤如下所述：

1）根据某地域特点，将其分为若干子区域，并将各风区划分至各子区域。结合子区域内各风区海上风电规模和各风区小时级海上风电出力原始曲线，通过加权求和的方式可以得到子区域的小时级海上风电出力原始曲线，公式如下：

式中：

$ {A_t} $ ——各子区域小时级海上风电出力原始曲线，(t=$1, 2, \cdots, 8\;760 $)；

I ——该子区域内的第i个风场；

m ——该子区域内风场总数目；

$ {P_{it}} $ ——第i个风场的出力原始曲线(t=$1, 2, \cdots, 8\;760 $)。

2）得到夏季反调峰特性曲线簇。将各子区域$ {A_t} $(t=$1, 2, \cdots, 8\;760 $)夏季(5~10月)184条海上风电日出力曲线对日负荷峰谷差的加剧程度按大到小进行降序排列，挑出反调峰特性曲线，即反调峰特性指标大于5%的日出力曲线，形成一类夏季反调峰特性曲线簇。反调峰特性指标的计算公式如下：

式中：

γ_sum ——夏季海风日出力曲线的反调峰特性值；

$\Delta {L_{{\rm{net}}}}$ ——净负荷曲线峰谷差，净负荷曲线为日负荷曲线减去海上风电日出力所形成的曲线；

$ \Delta {L_0} $ ——日负荷曲线峰谷差；

$ {p_{\max }} $ ——当日海上风电出力最大值。

3）对经过步骤2处理后中各子区域$ {A_t} $(t=$1,2,\cdots, 8\;760 $)剩余的海上风电日出力曲线按照波动趋势和出力特性进行分类，得到若干曲线簇。分类方法考虑采用高斯混合模型，利用公式（3），设定K个高斯分布，每个高斯分布线性叠加得到高斯混合模型概率密度函数。

4）确定高斯混合分布所得到的合理的曲线簇分类个数。高斯混合分布可以将各子区域的小时级海上风电出力曲线分为指定的K类，但合理的K值却无法由高斯混合分布给出。采用公式（8）确定合理的曲线簇分类数目，保证对原始数据的合理分类。

5）基于曲线簇分类结果，利用箱型图对包括反调峰特性曲线簇在内的数据进行筛选和迭代，得到各曲线簇的代表性曲线。分析各曲线簇数据的中心位置和散布范围，并计算数据间的离散程度、异常值和分布差异等，最终每个曲线簇得到一条代表性曲线。

6）拟定各子区域不同的海上风电出力情景。对步骤5中所得到的子区域内各条海上风电出力代表性曲线所表征的曲线簇进行月份特征统计，在此基础上得到各月份所对应的海上风电出力代表性曲线。代表性曲线的选取原则考虑如下：（1）若夏季较为集中出现某条代表性曲线，则以此条曲线代表夏季海风日出力特性，特别地，对于夏季若出现不同代表性曲线并且概率较为接近的情况，则以不同曲线代表夏季海风日出力特性；（2）若冬季较为集中出现某条代表性曲线，则以此条曲线代表冬季海风日出力特性，特别地，对于冬季若出现不同代表性曲线并且概率较为接近的情况，则以不同曲线代表冬季海风日出力特性；（3）同时对夏季以及冬季得到的代表性曲线进行组合，并结合概率统计特性，由此形成不同的各子区域全年海上风电出力情景。表示如下：

式中：

${{\rm{SCE}}_i}$ ——第i个出力情景；

${{\rm{Sum}}_m}$ ——夏季代表性曲线m；

${{\rm{Win}}_n}$ ——冬季代表性曲线n。

于是，所形成的各出力情景的概率值公式如下：

式中：

$ {\beta _i} $ ——第i个出力情景的概率值；

${N_{{{\rm{sum}}_m}}}$ ——夏季代表性曲线m所在曲线簇中夏季曲线总条数；

${N_{{{\rm{win}}_n}}}$ ——冬季代表性曲线n所在曲线簇中冬季曲线总条数；

$N{0_{{\rm{sum}}}}$ ——各条夏季代表性曲线所在曲线簇中夏季曲线总条数；

$N{0_{{\rm{win}}}}$ ——冬季代表性曲线所在曲线簇中冬季曲线总条数。

7）对各不同情景i下的全年的海上风电出力曲线进行修正。不同出力情景下，应保证全年的海上风电利用小时数与各子区域小时级海上风电出力所得到的利用小时数一致。利用原始利用小时数与不同出力情景下的利用小时数的比值作为修正因子，并对情景内各条出力特征曲线进行修正。公式如下：

式中：

${U_{{\rm{new}}}}_{i = 1}^{24}$ ——修正后的海风出力特征曲线；

${U_{{\rm{sce}}}}_{i = 1}^{24}$ ——修正前的海风出力特征曲线；

$ {T_{{\rm{ori}}}} $ ——各子区域小时级海上风电出力得到的原始年利用小时数；

$ {T_{{\rm{sce}}}} $ ——各情景海上风电特征曲线得到的修正前的年利用小时数。

海上风电出力的电量平衡计算方法流程如图2所示。根据上述获得的不同类别的海上风电出力特征曲线，根据各个出力情景的概率值通过加权平均法进行电量平衡计算，公式如下：

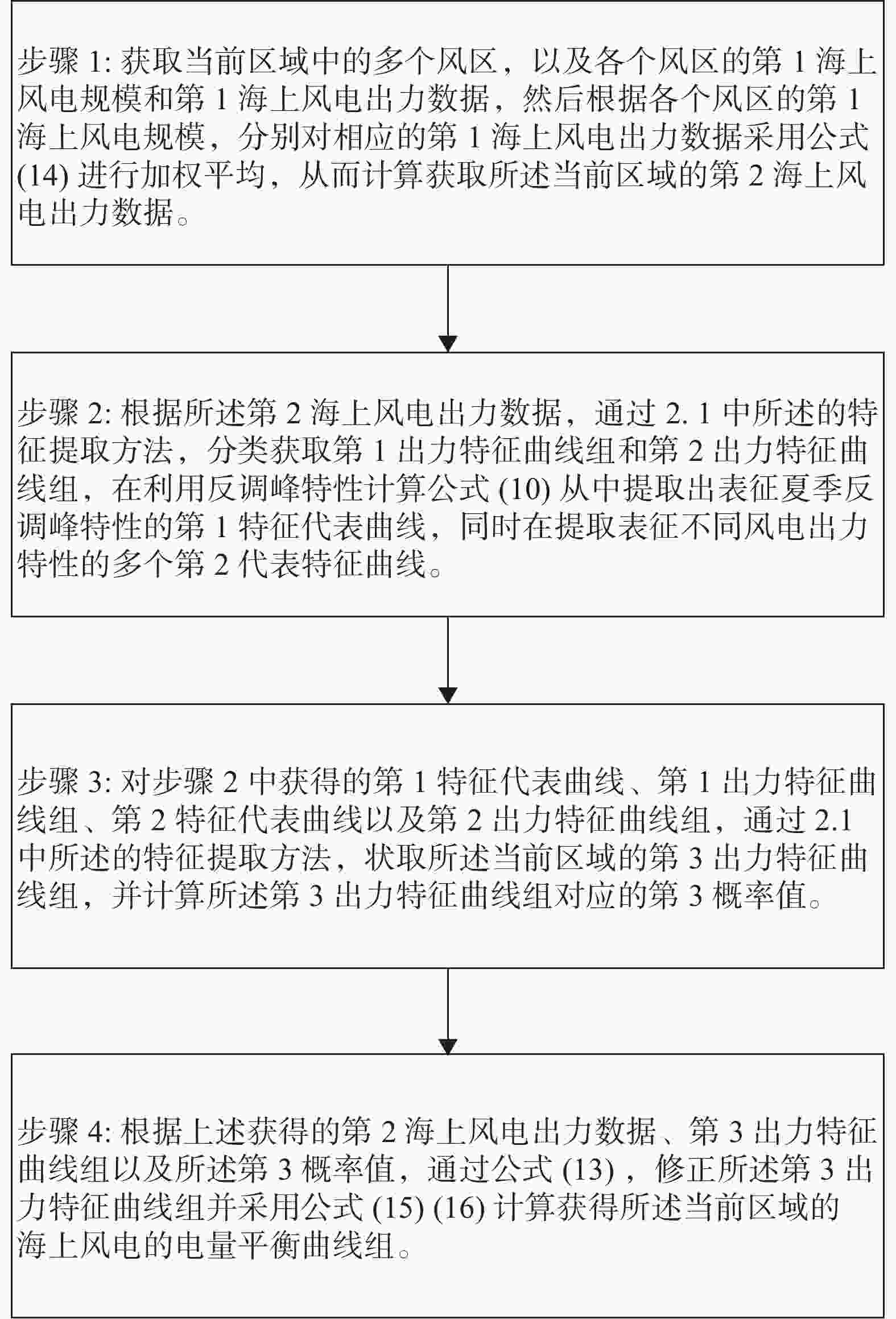
Figure 2.  Flow chart of calculation method for electric quantity balance of offshore wind power output

式中：

$ {a_i} $——风区i的第1海上风电规模占当前区域的海上风电总规模的比重。

式中：

Q ——当前区域的海上风电的电量平衡曲线组；

M ——第4出力特征曲线组；

Q_i ——根据与当前区域的全年海上风电出力情景i对应的第4出力特征曲线组所计算的电量平衡结果；

β_i ——与当前区域的全年海上风电出力情景i对应的第3概率值。

对于各类电源的利用小时数，按如下公式获得全年利用小时数：

式中：

$ P $——各类电源装机容量。

根据中国某省份的海上风电分布情况和海上测风数据（剔除不良测风塔测风数据）将全省海上风电划分为3个子区域，分别为子区域1、子区域2以及子区域3，并采用中国某省的海上风电原始出力曲线，按表1中海上风电装机15 GW规模下不同区域装机情况，拟合得到不同子区域风电出力率曲线。

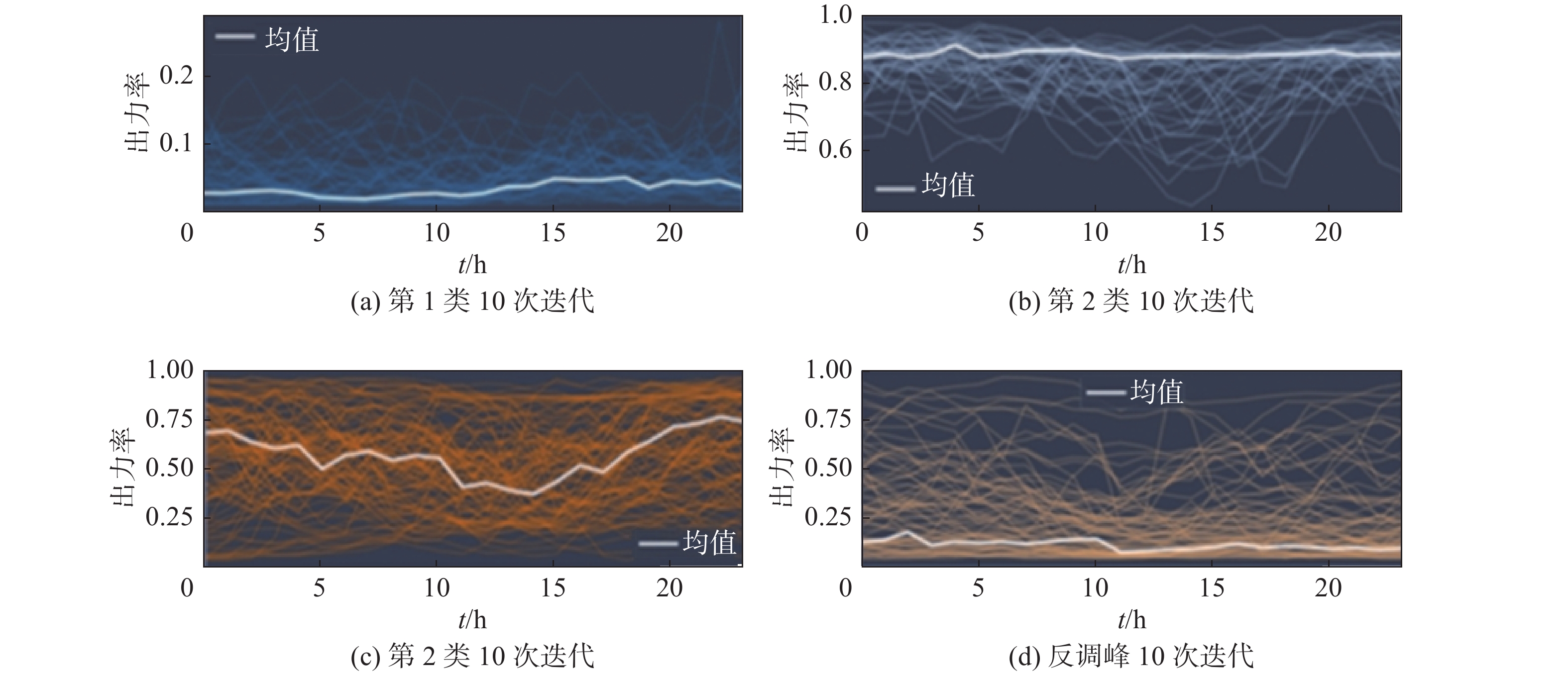
对中国某省份不同子区域内海上风电原始出力曲线，通过采用第2节所提的分类方法对各子区域的海上风电拟合出力曲线进行分类、筛选以及聚合处理，得到15 GW装机规模下各子区域曲线簇分类结果如图3~图4所示。从图中可以看出，子区域1能够聚类出1条反调峰和3类海上风电出力曲线，子区域2能够聚类出3类海上风电出力曲线，子区域3能够聚类出1条反调峰和2类海上风电出力曲线。

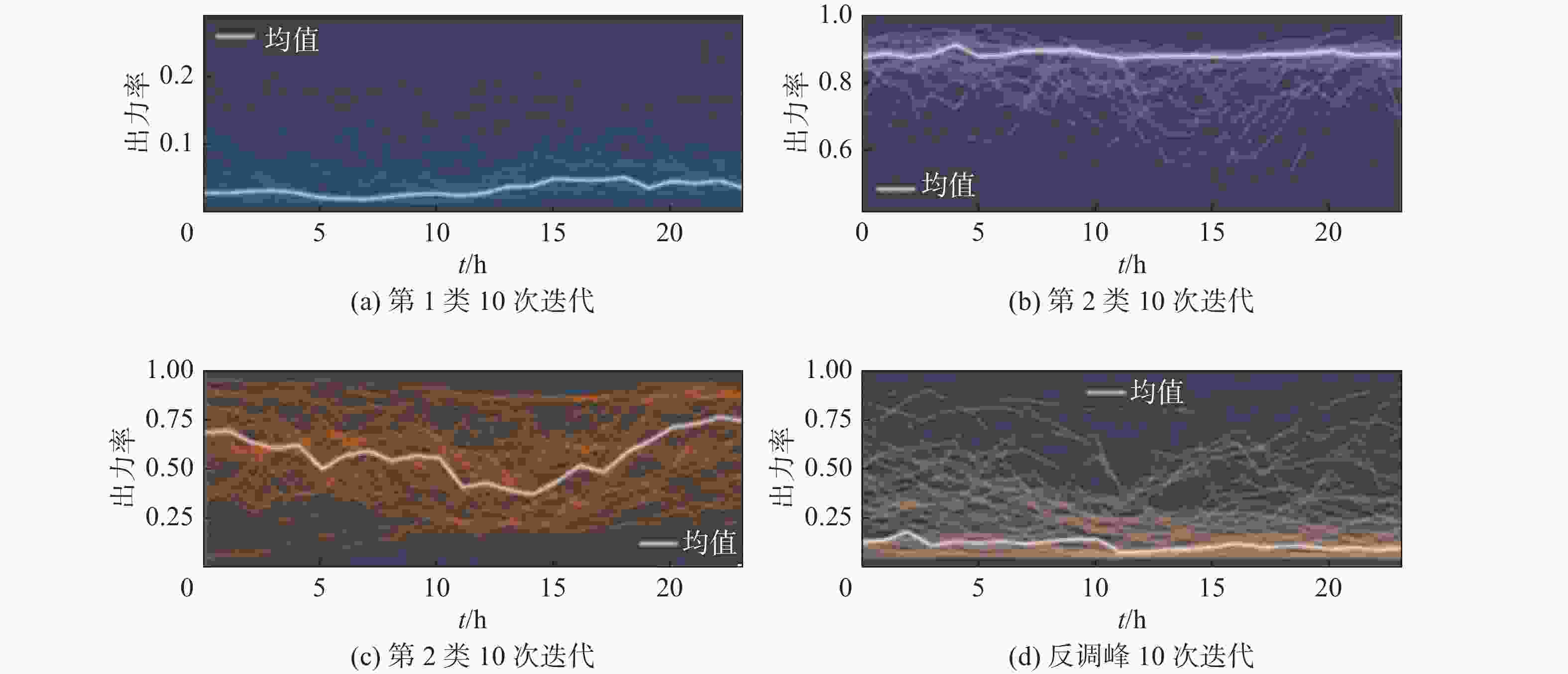
Figure 3.  Classification results of different curve group and characteristic curves of offshore wind power output in Area 1

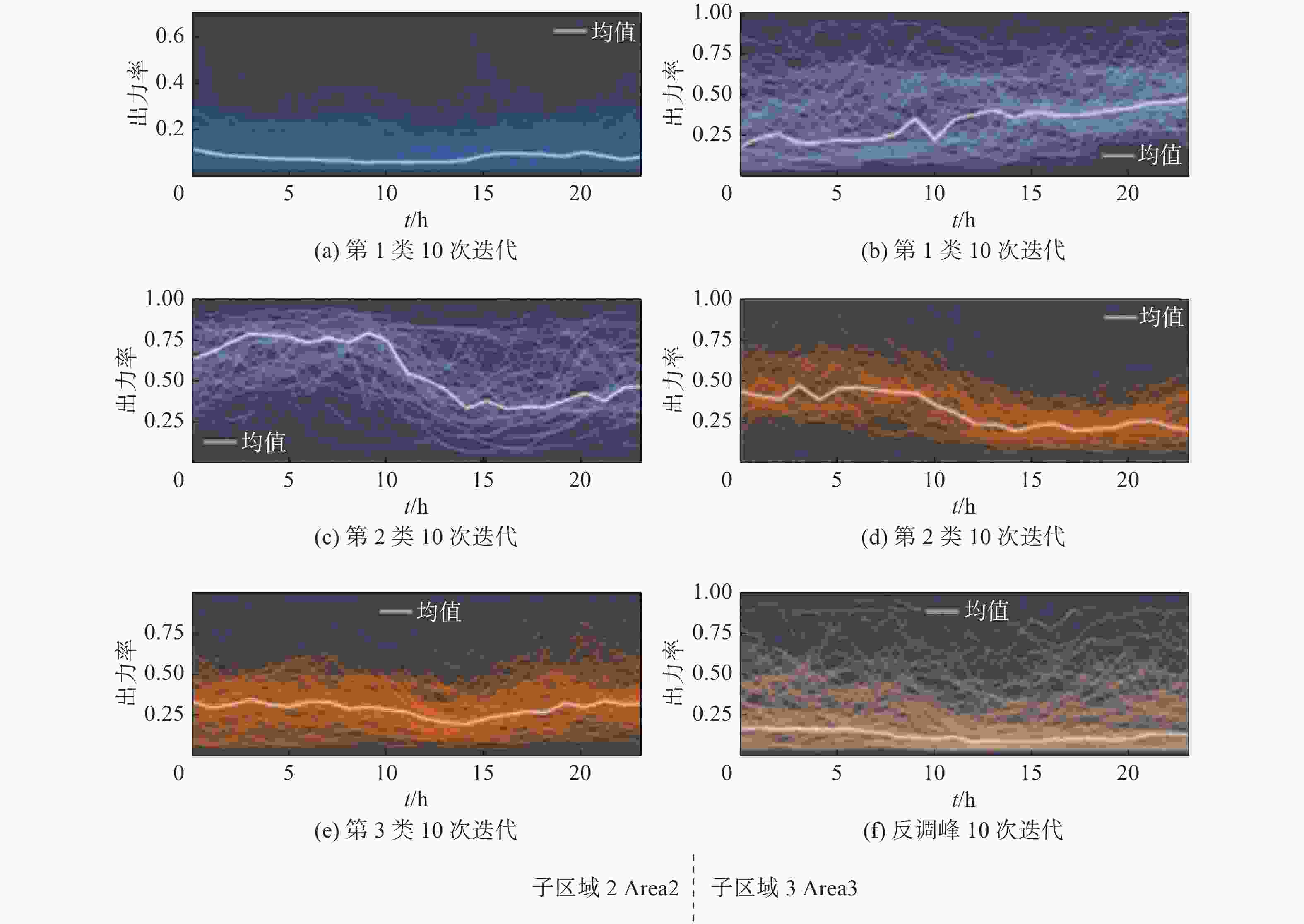
Figure 4.  Classification results of different curve group and characteristic curves of offshore wind power output in Area 2 and Area 3

对上述所得到的各子区域内各条海上风电出力代表性曲线所表征的曲线簇进行月份特征统计，在此基础上得到各月份所对应的海上风电出力代表性曲线。

区域1同种类海上风电日出力曲线的月份统计特性如图5所示，区域1在夏季5~10月份，反调峰特性曲线较为集中，共出现52条，占整个夏季曲线的比例为45%，另外3类曲线在夏季占比较低，于是仅考虑反调峰特性曲线作为区域1夏季代表性曲线。同理可知，区域1在冬季1~4月份以及11~12月份，第2类和第3类曲线分别出现38条（占比23%）和103条（占比63%），而反调峰及第1类曲线在冬季的占比较低，于是选取第2类和第3类曲线作为区域1的冬季代表性曲线。

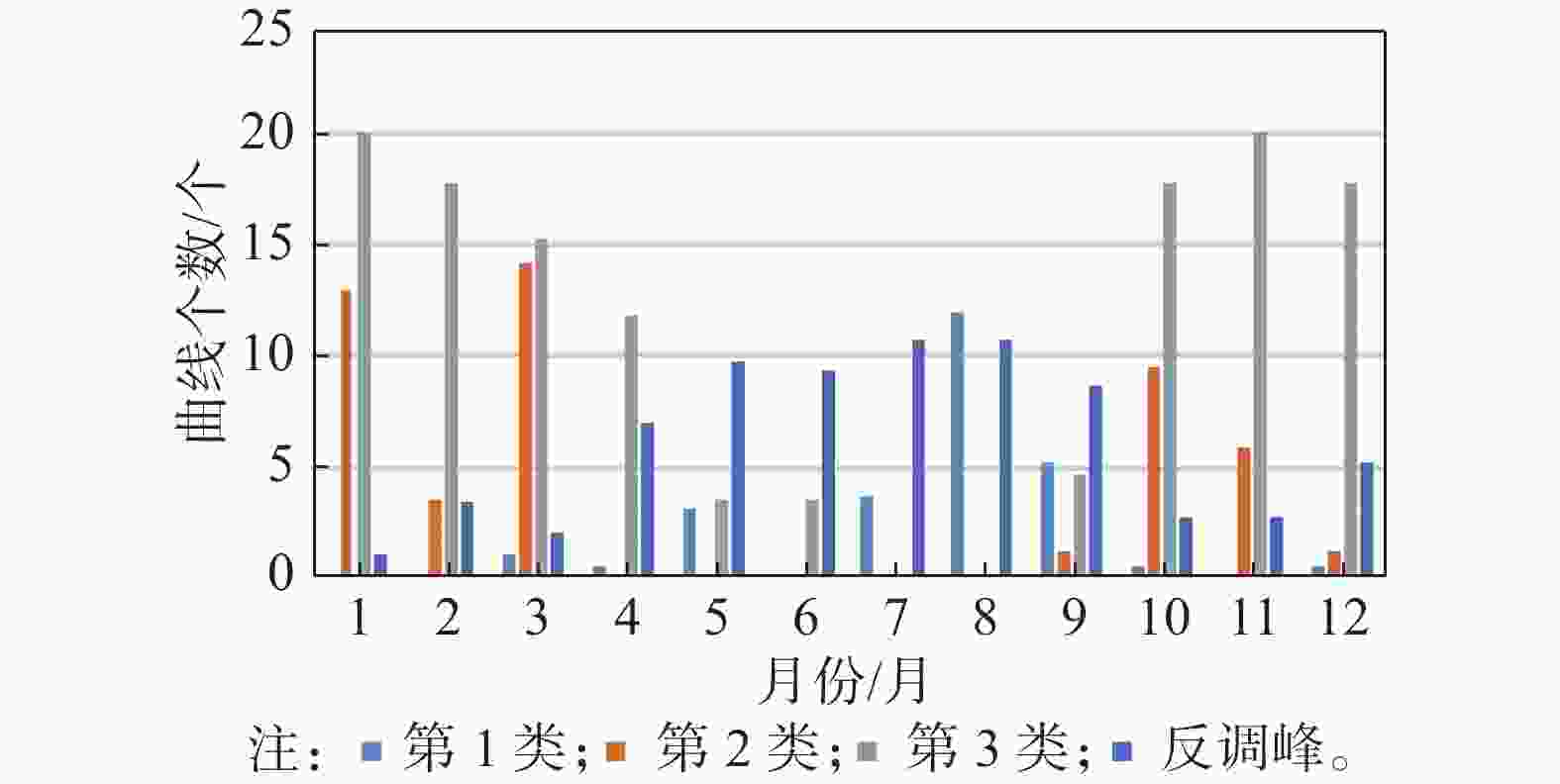
Figure 5.  Monthly statistical characteristics of daily output curves of different types of offshore wind power in Area 1

区域2不同种类海上风电日出力曲线的月份统计特性如图6所示，区域2在夏季5~10月份，第1类曲线较为集中，共有96条（占比52%），另外两类曲线在夏季占比较低，于是选取第1类曲线作为区域2夏季的代表性曲线。在冬季1~4月份以及11~12月份中，第2类和第3类曲线分别出现38条（占比23%）和103条（占比63%），而反调峰及第1类曲线在冬季的占比较低，于是选取第2类和第3类曲线作为区域1的冬季代表性曲线。

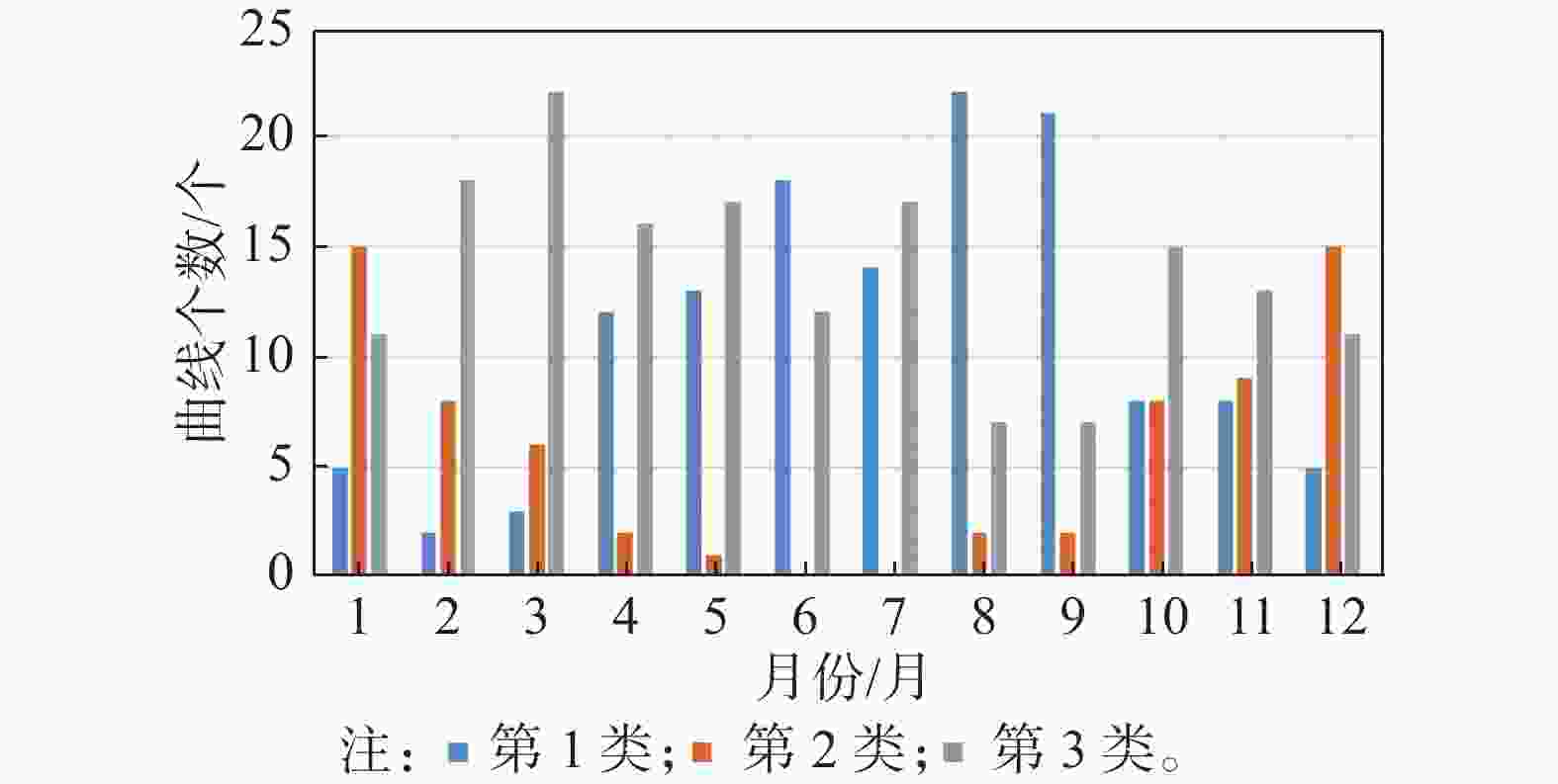
Figure 6.  Monthly statistical characteristics of daily output curves of different types of offshore wind power in Area 2

区域3不同种类海上风电日出力曲线的月份统计特性如图7所示，区域3在夏季5~10月份中，海上风电曲线类型中以反调峰特性曲线占比为54%，共75条，其余曲线占比较低，故选取反调峰曲线作为区域3夏季的代表性曲线。在冬季1~4月份以及11~12月份中，第1类和第2类曲线分别为58条（占比40%）和60条（占比42%）而反调峰特性曲线在冬季占比较低，故选择第1类和第2类曲线作为区域3的冬季代表性曲线。

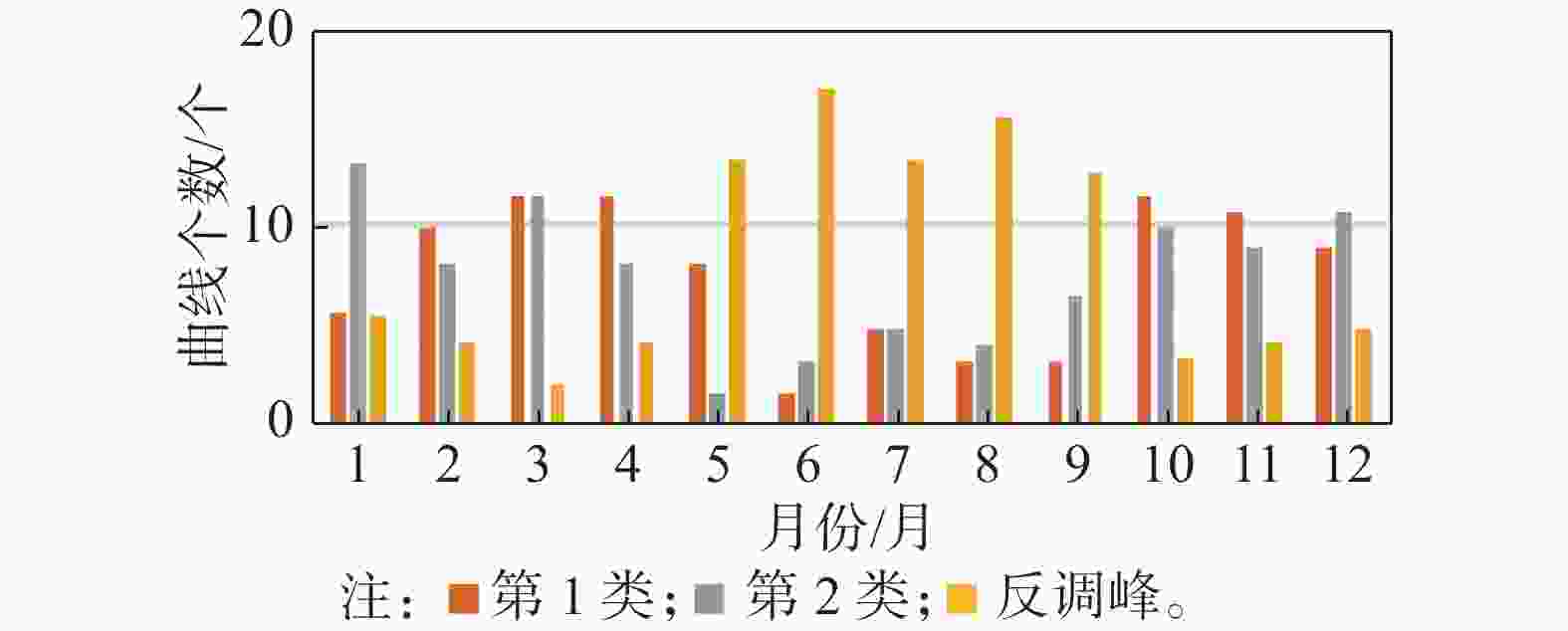
Figure 7.  Monthly statistical characteristics of daily output curves of different types of offshore wind power in Area 3

区域的全年海上风电出力曲线由一条夏季海上风电出力曲线和一条冬季海上风电出力曲线组成，因此结合上述中各区域所取的夏季与冬季海上风电出力代表性曲线，可以组合出各区域的全年海上风电出力场景，如表2所示。

将该省份3个区域出现的场景进行组合，获得全省海上风电15 GW装机规模下各情景分类统计结果以及概率特性，如表3所示。

对表3中获得的4个场景中全年海上风电代表性出力曲线，考虑其各自的权重，利用公式（15）和公式（16），得到全年电量平衡和利用小时数结果，如表4所示。

结合海上风电各类组合场景曲线，在综合考虑各类组合场景中海上风电各类反调峰曲线中发现，海风曲线各类场景中不存在电量不足现象，且在情景3和4中出现少量弃风电量，处于较低水平，整体处在合理范围内，从调峰能力看，抽水蓄能电站利用小时数较低，在300~340 h之间。整体来看，15 GW海上风电规模下，各分区海上风电电量消纳良好，不会导致大规模弃风。

本文提出了一种基于高斯混合聚类的海上风电出力特征曲线提取方法，并将其应用在电量平衡及弃风电量计算。本文的主要结论如下：

1）通过基于BIC的GMM算法，提出了全新的基于不同海风区域和不同出力特性情况进行分类迭代的特征曲线提取方法，比传统的典型场景聚类方法更全面，能合理给出表征海上风电出力的典型特征曲线。

2）根据海上风电出力曲线聚类结果，开展了不同类型海风曲线对应的电量平衡计算，通过概率加权的方式获得全年的弃风电量、各类机组利用小时数等指标，并通过计算实例分析验证了方法的可行性与合理性。

该方法提升了电量平衡及弃风电量计算的准确性，为后续电力系统规划及电网运行提供更准确的数据支持，助力新能源高效消纳和电力可靠供应。