-
大直径单桩的自沉现象是指桩靠自重深入海床土层的深度。溜桩现象指在打桩的过程中,桩基础突然不受控制的自行下沉过程。溜桩和自沉是同一种机理,都是由于桩土作用力无法承受桩和打桩设备的重量,在重力作用下桩基础下沉的现场。溜桩也可以看作是打桩过程中不受控制的自沉,即广义上的自沉。
我国海上风电基本采用无过渡段单桩基础,即钢管桩一直延伸到海面以上与风机塔筒相连。欧洲地区海上风电基本采用单桩基础加过渡段的形式,单桩顶部大多不露出海面,风机塔筒底部与单桩桩顶有过渡段连接。无过渡段单桩施工工序简单,但因为桩基础本身包含了从海床到法兰面的所有钢材重量,桩基础的整体自重较大。
欧洲地区海域地质条件相比广东海域更好,由于地质历史上的冰川作用,欧洲地区广泛分布有超固结的硬粘土和密实砂,土的强度较高,单桩基础的自沉并不是很显著的问题。广东海域广泛分布欠固结和正常固结的软粘土,强度较低,加上无过渡段单桩基础的自重较大,因此无过渡段单桩基础的自沉和溜桩的风险十分显著。施工过程中突然发生的自沉和溜桩会威胁施工设备安全、损坏稳桩设备、损坏打桩锤、带来额外的设计风险,造成经济和工期的损失。能够合理地预测自沉和溜桩的风险对我国的海上风电工程就显得尤为重要。
国内外关于大直径单桩自沉与溜桩做了很多相关研究,尹汉军[1]等人基于能量守恒提出了采用静力平衡法计算溜桩长度,他利用能量守恒法计算桩周侧摩阻力,利用别列柴策夫公式计算桩端阻力,引入了动力效应系数影响因素。贾沼霖[2]、徐玉[3]认为工程沉桩过程中高估了动侧摩阻力值,低估了端阻力值,然后基于API规范提供的方法针对黏土进行端阻力评估,建议采用静力触探等工程手段提取土壤参数用于计算。张曦[4]等人针对大直径单桩嵌岩施工时提出了溜桩对策以及溜桩后的处理工程方案;崔永忠[5]等人基于CPT数据针对广东某风场利用API 2GEO里面提供的方案进行大直径单桩自沉的预测,为实际施工提供参考。闫澍旺[6-7]等人针对溜桩现象,结合实际工程对溜桩的过程和发生机理进行了探讨,提出了在溜桩状态下土阻力的计算方法,在此基础上,建立了判断溜桩范围的分析计算方法;利用CAPWAP软件针对海洋平台桩基工程沉桩过程中的极端现象进行了分析计算,验证了所提出的方法的合理性,可供桩基设计以及沉桩施工参考。
国外的研究文献中,打桩过程中的土阻力计算目前最为常用的方法包括Toolan和Fox (1977)[8]、Stevens等(1982)[9]、Alm和Hamre(1998,2001)[10-11]。规范API 2GEO针对海洋石油平台桩基结构提供了推荐做法。除此之外,DNV RP C212[12]推荐了基于CPT端阻估算桶基础的自沉深度的方法,但仍然要考虑到岩土条件变化和基础形状变化带来的影响。
本文以API规范为基础,结合工程实际沉桩和溜桩数据,对规范折减系数进行修正,利用统计方法,提出适合国内南海淤泥质海床的参数选取方法。
-
在单桩基础下沉过程中,由于直径很大,因此产生土塞的概率非常低。只需要考虑桩的外侧壁、内侧壁和桩端部环形面积会受到土的阻力作用
$ R $ ,以及桩的下沉力。下沉力包括桩身的自重以及惯性力。当桩自沉停止的时候,惯性力为0,土的阻力与桩的自重接近处在静力平衡的状态。因此我们在实际的计算中认为当土阻力$ R $ 小于桩的自身重力$ W $ 的时候,桩会继续下沉,当土阻力$ R $ 大于桩的自身重力$ W $ 的时候,桩就会停止下沉。因此计算中认为阻力与重力相等时,即:$$ R=W $$ (1) 式中:
$ R $ ——桩总阻力;$ W $ ——桩自重。单桩的插入深度即为单桩自沉深度。
表1列出各种岩土条件组合和可能的风险。
岩土情况组合 深厚粘土 深厚
砂土粘土下方
砂土砂土下卧
粘土层可能的
风险自沉深度大,
自沉速度过快低风险 低风险 出现溜桩 Table 1. The risk identification table of self-weight penetration and pile running
工程实践表明,溜桩通常会在桩从承载力较高的土层打入到承载力小的土层时发生。溜桩的深度、速度与土壤特性及桩身自重等有很大关系。打桩过程中,针对软硬土层交替出现的地质条件,大直径钢管桩容易溜桩,一般当土的总阻力小于桩身自重、小于桩与锤总重或者小于桩与锤的惯性力时,容易发生溜桩现象。
-
下沉过程桩土阻力由桩端阻力和桩侧阻力组成。桩在下沉过程中,桩土之间有连续的相对位移,此时桩侧摩阻力小于桩在承载状态下的桩侧摩阻力。Toolan和Fox(1977)[8]认为沉桩过程中粘土中的桩侧阻力应使用粘土的重塑强度。砂土由于渗透系数高,超孔隙水压力消散很快,砂土中的桩侧阻力与静载下的桩侧阻力相近。考虑锤击的动荷载效应,沉桩过程中的桩端阻力高于静载下的桩端阻力。Alm和Hamre (1998,2001)[10-11]对直径2.5 m的超长桩沉桩做了详细研究,引入了桩土“摩擦疲劳”的概念,认为桩侧阻力不是一个恒定值,随着桩端贯入深度的增加,某一深度处的桩土作用力会成非线性降低。Alm和Hamre(1998,2001)[10-11]提出了一个基于CPT参数的用于估算桩侧阻力随着桩端贯入深度成指数关系的公式。Randolph等(1994)[13]系统性地研究了砂土中的桩基承载机理,在文中他们也提出了某一深度处的桩侧阻力随桩端贯入深度的增加成指数关系降低。
桩侧阻力可以基于API静载下桩基础承载力的计算方法进行预测。其中,粘土中的侧阻力采用重塑粘土的不排水抗剪强度,砂土中的水平侧压力系数取为0.5,其余的系数计算依旧遵循API的相关规定。需要的设计参数包括粘土的不排水抗剪强度
$ {S}_{\mathrm{u}} $ 、粘土的重塑强度$ \varPsi $ 、砂土的摩擦角$ \delta $ 。粘土的重塑强度与粘土的不排水抗剪强度有线性比例关系,用粘土设计强度折减系数$ {S}_{\mathrm{r}} $ 表示。不同粘土有不同的折减系数$ {S}_{\mathrm{r}} $ 。本文将基于实际桩基打桩样本数据,基于API基本方法,利用统计学方法,给出适用于广东海域粘土地质条件下,预测大直径单桩自沉和溜桩深度的折减系数。表2列出了API规范提到的打桩过程中土阻力的计算方法。其中
$ {S}_{\mathrm{r}} $ 为桩土侧摩阻计算时的强度折减系数。该值的选取直接决定预测的准确性。参数 粘土 砂土 侧摩
阻力 $ f $$ f=\alpha {S}_{\mathrm{u}}/{S}_{\mathrm{r}} $
式中:
$ \alpha =\left\{\begin{array}{c}0.5{\varPsi }^{-0.5}(\varPsi \le 1)\\ 0.5{\varPsi }^{-0.25}(\varPsi > 1)\end{array}\right. < 1 $
$ \varPsi =\dfrac{{S}_{\mathrm{u}}}{{p}_{0}^{\prime}} $$ f=0.5{p}_{0}^{\prime}\mathrm{t}\mathrm{a}\mathrm{n}\delta $ 端阻力 q $ q=7.5{S}_{\mathrm{u}} $ $ q={N}_{\mathrm{q}}{p}_{0}^{\prime} $ 注释 $ {S}_{\mathrm{u}} $——粘土不排水抗剪强度(kPa);
$ {p}_{0}^{\prime} $——上覆有效压力(kPa);
$ {S}_{\mathrm{r}} $——粘土强度折减系数(-)。$ \mathrm{t}\mathrm{a}\mathrm{n}\delta $——桩土摩擦角的正切值(-);
$ {N}_{\mathrm{q}} $——无量纲支撑能力系数(-)。Table 2. SRD calculation methods and parameters description
-
某海上风电场项目位于广东沿海海域,临近珠江口。场区地层上部主要为第四系全新统海相沉积的软粘土层,其下为第四系晚更新统海陆交互沉积地层,呈粘土与砂土层交互分布,下部主要为砂土层。水深范围在11~21 m,大直径单桩直径7.25~8.5 m,单桩自重在1 000~1 400 t之间,CPT勘测站位15个,锤重约750 t。
-
本项目已有的46个单桩基础的平均自沉深度23.2 m,最大深度40.77 m,最小深度11.1 m。自沉的数据统计见表3。
自沉深度/m 数量 <15 7 15~20 9 20~25 13 25~30 8 30~35 5 >35 4 Table 3. Project summary recorded of monopiles self-weight penetration
根据项目实际沉桩数据和工程反馈,该项目具有如下特点:
1)海底上部以软粘土为主,自沉深度大,在下放桩基础及压锤的过程中需小心控制下沉过程。
2)桩穿过较硬的土层进入到较软层容易再次自沉即溜桩,比如硬粘土或砂土层下有强度较低的粘土层,该场区存在多个类似土层分布的机位。
为了更清楚地显示自沉和溜桩对沉桩的影响,这里计算自沉和溜桩长度占桩基础入泥深度的百分比,如图1与图2所示。横坐标是自沉深度或溜桩长度占桩基础入泥深度的百分比,纵坐标是个数。
-
从图1可以看到,自沉深度与桩入泥深度占比至少为20%,其中占比为40%~50%的数量最多,个别桩的自沉深度达到了设计入泥深度的80%,几乎“一溜到底”。绝大部分机位的单桩基础自沉占比为20%~50%。从图2可以看出,自沉稳定开始锤击沉桩后,溜桩长度大部分在10%以内。从欧洲经验来看,欧洲风场桩基普遍自沉深度在3~5 m之间,广东海域单桩自沉与欧洲的情况差别较大的原因主要是:
1)欧洲北海岩土条件较好,广泛分布有超固结的硬粘土和密实砂,土的强度较高,土阻力因此也较高,广东海域,特别是珠江口区域分布深厚的欠固结和正常固结软粘土,土的强度较低,土阻力低[14]。
2)国内单桩多采用无过渡段设计[15],单桩的整体自重较大,国外单桩基础重量在800 t左右,本文提到项目单桩均重在1 300 t左右。
总体而言,广东海域的单桩自沉和溜桩情况比欧洲要严重,风险更高,施工器械和施工方案针对大幅度自沉和溜桩现象要做充足的预案工作。自沉和溜桩问题在欧洲较少出现,风险很低,因此针对自沉的研究资料较少,但是自沉在广东海域是一个不容忽视的风险,钢管桩自沉过大,对导向架设计、钢管桩垂直度控制等都有明显影响,故广东沿海海域,钢管桩自沉量的预测和计算,是保证施工质量的重要内容。
API规范现有的推荐方法,里面的折减系数是基于海洋油气平台的小直径钢管桩经验反算获得,对大直径单桩基础不适用。如下章节将利用实际桩基础自沉和溜桩深度数据,结合地勘参数的选取,修正API方法里面的粘土强度折减系数
$ {S}_{\mathrm{r}} $ ,进而为后面的工程提供参考。 -
$$ J=\frac{1}{m}\sum ({y}^{*}{-y)}^{2} $$ (2) 式中:
$ J $ ——误差函数;$ m $ ——样品数量,即参与计算的基础个数(个);$ {y}^{*} $ ——利用API方法预测自沉或溜桩深度(m);$ y $ ——实际自沉或溜桩深度(m)。 -
大直径单桩自重大,桩径大,桩侧面积大,桩端截面积小,根据《建筑桩基技术规范》,本项目下沉的时候基本不会产生土塞。工程经验表明,粘土中的桩土阻力主要由桩侧阻力组成,桩端阻力影响很小,所以单桩在粘土层中自沉较大。砂土中的桩土阻力,桩端阻力的影响不可忽视,所以单桩在砂土层中自沉相对较小的距离就会稳定。本次重点研究粘土设计强度折减系数在本项目中对单桩基础自沉和溜桩的影响。
单桩的下沉力包括了与下沉速度有关的惯性力,在第一次自沉的时候,施工单位会缓慢放松吊缆,下沉速度较慢,惯性力作用不明显,但是溜桩发生的时候,桩下沉的速度通常是无法控制的,因此实际溜桩深度会比实际土阻力等于桩自重的位置更深。本次分析中的粘土设计强度折减系数综合考虑了惯性力的影响。
-
$ {S}_{\mathrm{r}} $ 预取值区间为[1,8],利用表2中API的计算方法,分别评估这46个机位的自沉深度,并统计每一个$ {S}_{\mathrm{r}} $ 取值时候的误差函数值,见图3。从图3可以看到$ {S}_{\mathrm{r}} $ =2的时候,误差最低。粘土设计强度折减系数在工程上等价于粘土的灵敏度。如图4所示,根据CPT数据推导本项目的粘土灵敏度大部分处在[1,3]的区间内,20 m深度范围内部分灵敏度处在[3,4]之间,深度20 m后的灵敏度基本处在[1,3]之间。从图3中可以看出,当
$ {S}_{\mathrm{r}} $ 等于4的时候,误差函数开始快速升高。基于本项目的数据,在评估单桩自沉深度的时候,取$ {S}_{\mathrm{r}} $ 区间的下限为1,上限取[3,4]是比较合理的。$ {S}_{\mathrm{r}} $ 能够取1的原因是考虑到设计参数的选取会偏于保守。 -
$ {S}_{\mathrm{r}} $ 初取[1,8]不同的值,分别计算这46个机位中,深度最大的一次溜桩的终止深度,与实际沉桩中最后一次溜桩的终止深度比较,计算误差函数。从图5可以看出,当$ {S}_{\mathrm{r}} $ =5的时候,误差最低。从实际工程的角度考虑,用于评估溜桩发生的最大深度时,取$ {S}_{\mathrm{r}} $ 区间的下限为[3,4],上限取[6,7]是比较合理的。 -
用于计算溜桩的最大深度或总长度的
$ {S}_{\mathrm{r}} $ 取值比计算自沉深度时的$ {S}_{{\rm{r}}} $ 取值高出很多,意味着在溜桩的时候粘土强度的折减比最开始自沉的时候强度折减严重很多,这应该是桩周土“摩擦疲劳”的效应。White等(2004)[16]总结“摩擦疲劳”指的是在循环荷载作用下,桩土界面处的作用力降低的过程。White等(2004)[16]通过一系列离心机试验发现在持续单向荷载作用下并没有明显的摩擦疲劳的现象,但是在循环荷载作用下均观测到了明显的摩擦疲劳现象。他们分别用恒定荷载、加载-卸载循环、大荷载加载-卸载-反向加小荷载的方式将模型桩植入到砂土中。在恒定荷载压桩的时候,没有发现明显的摩擦疲劳。在两种循环加载的试验中,砂土存在明显的摩擦疲劳现象。在本项目中,单桩在重力作用下自沉的过程,可以看作是恒定荷载压桩的过程,此时桩周土的强度可以看作是重塑土的强度。当自沉稳定后,开始锤击沉桩,桩土界面受加卸载的循环作用力,桩周土出现摩擦疲劳,桩周土的强度从重塑土强度进一步降低。因此在锤击后溜桩的时候,土的阻力降低比自沉的时候更严重。
-
从本项目实际工程数据得到的
$ {\mathit{S}}_{{\rm{r}}} $ 取值范围较大。在评估自沉深度时,$ {\mathit{S}}_{{\rm{r}}} $ 取值下限为[1,3],上限为[3,4]。在评估溜桩发生深度时,$ {\mathit{S}}_{\mathbf{r}} $ 取值下限为[3,4],上限为[6,7]。出现这种情况的原因包括:1)本次确定
$ {\mathit{S}}_{\rm{r}} $ 的取值属于根据实际沉桩数据反算得到的,最终取值与能否基于准确的粘土不排水抗剪强度有很大关系。由于客观条件限制,海洋勘察能够采取的手段比较局限,因此部分粘土的设计不排水抗剪强度可能与实际强度有偏差,影响了$ {\mathit{S}}_{\rm{r}} $ 取值。2)本场区表层粘土强度较低,部分机位自沉以及溜桩的深度受密实砂层的埋深影响较大,影响了
$ {\mathit{S}}_{\rm{r}} $ 的准确取值。比如在计算溜桩深度的时候,可以看到当$ {\mathit{S}}_{\rm{r}} $ 取值超过4的时候,$ {\mathit{S}}_{\rm{r}} $ 的增长对溜桩深度影响开始变得不明显,此时可以认为无论$ {\mathit{S}}_{\rm{r}} $ 取值怎样变化,溜桩深度更多的取决于砂层的埋深。 -
本文的结果主要面向实际的施工应用,对自沉和溜桩进行初步风险评估,建议分别针对表4中三种情况进行分析。
情况分类 $ {\mathit{S}}_{\rm{r}} $取值 最乐观情况 1或2 最可能情况 3或4 最不利情况 6或7 Table 4.
$ {\mathit{S}}_{\rm{r}} $ comprehensive application recommendations当桩基影响深度范围内地层条件为粘土下卧较厚砂层时,可以考虑最乐观情况和最可能情况评估单桩自沉深度。当粘土和砂土交替出现的时候,还应使用极端情况评估可能的溜桩风险,及时提前采取措施预防设备损坏或沉桩超过设计深度。
-
常用的CPT结果
$ {q}_{\mathrm{n}\mathrm{e}\mathrm{t}} $ 与粘土不排水抗剪强度$ {S}_{\mathrm{u}} $ 之间的关系是:$$ {S}_{\mathrm{u}}=\frac{{q}_{\mathrm{n}\mathrm{e}\mathrm{t}}}{{N}_{\mathrm{k}\mathrm{t}}} $$ (3) $ {N}_{\mathrm{k}\mathrm{t}} $ ——经验系数,取值分布在[15,25]之间。通过对比本场地的粘土设计强度与CPT的$ {q}_{\mathrm{n}\mathrm{e}\mathrm{t}} $ ,发现二者之间的关系可以较明显分成两组。第一组的粘土设计强度与CPT的$ {q}_{\mathrm{n}\mathrm{e}\mathrm{t}} $ 之间比例关系$ {N}_{\mathrm{k}\mathrm{t}} $ 约为[20,50]之间;第二组的第一组的粘土设计强度与CPT的$ {q}_{\mathrm{n}\mathrm{e}\mathrm{t}} $ 之间比例关系$ {N}_{\mathrm{k}\mathrm{t}} $ 远超过50。本次选取了两个有代表性的数据作为示例,如图6和图7所示。这里定义第一组为高设计参数,第二组为低设计参数。这里需要强调的是,CPT结果只是作为确定设计参数的重要依据之一,设计参数的最后取值需要综合考虑多方面因素[17]。分别分析两组中不同的设计强度折减系数
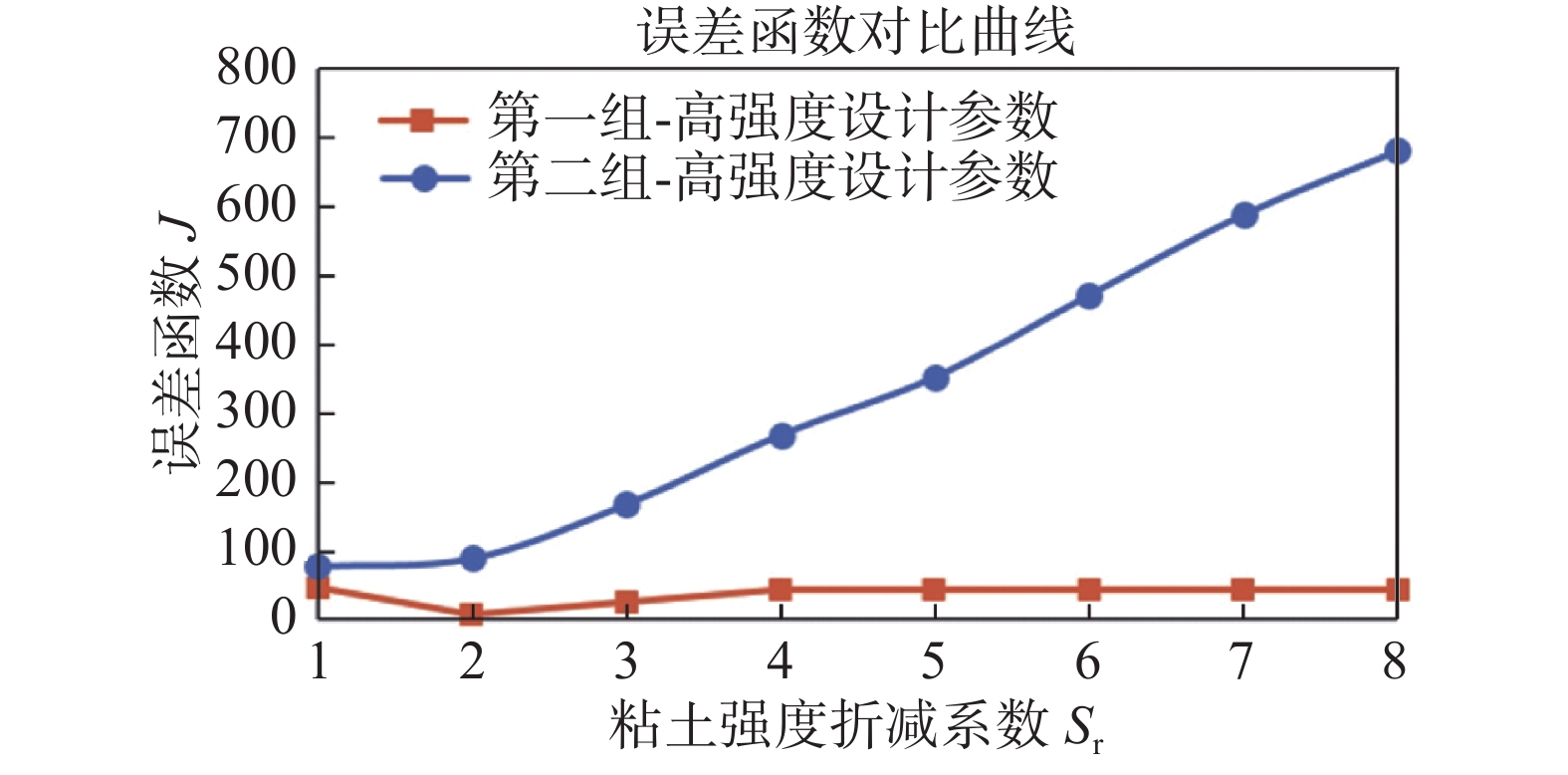
$ {S}_{\mathrm{r}} $ 下误差函数的值,得到如图8的结果。高设计强度参数分组的误差函数远小于低设计强度参数分组,在一定程度上说明高强度参数的取值更贴近现场实际粘土的原位不排水抗剪强度。分析全部46个单桩基础的自沉情况,设计强度折减系数$ {S}_{\mathrm{r}} $ 取2的时候,误差函数最小,这个与高设计强度分组的情况是类似的。对于低设计强度分组,当设计强度折减系数$ {S}_{\mathrm{r}} $ 取值在1~2之间时,误差函数结果约为100,当设计强度折减系数$ {S}_{\mathrm{r}} $ 取值超过3后,误差函数结果单调增加至约250。在高设计强度分组中,误差函数值最大约为50。进一步说明高设计强度取值下的计算与实际误差更小,高设计强度取值更加贴近原位强度。
Figure 8. Error function of self-weight penetration vs
$S_{{\rm{r}}} $ in two design strength parameter groups在高强度分组中,设计强度折减系数
$ {S}_{\mathrm{r}} $ 取值超过3后,误差函数值基本不变,可能是由于桩稳定在了某一砂层,因此无论前面粘土怎样折减,计算与实际之间的差别也不会有显著增长。而在低设计强度分组中,由于设计强度本身已经相对原位情况做了较大折减,当设计强度折减系数$ {S}_{\mathrm{r}} $ 继续增加的时候,上部计算粘土强度过低,单桩的计算自沉深度穿过了实际稳定的砂层,进入下部地层,因此误差函数稳定增加。通过以上分析,在一定程度上从单桩的自沉的角度验证了CPT测试数据是合理和可靠的。因此,在海上风电中加强CPT的应用,既可以优化基础设计,也可以帮助施工沉桩的分析预判,有效降低施工沉桩风险[17]。
-
本文结合广东沿海某海上风电项目的实际沉桩数据,分别对初始自沉以及溜桩风险进行了对比分析。根据现场资料,反向得到的粘土折减系数
$ {S}_{\mathrm{r}} $ 的取值参考范围,对广东海域大直径单桩自沉及溜桩风险的预判有很强的指导意义。综上所述还可以得到以下结论:1)国内由于基础形式、海床地质条件的特殊原因,单桩自沉深度能够占到设计深度的20%~50%,溜桩长度基本在设计深度的10%~30%,因此大直径单桩的自沉和溜桩是一个需要引起足够重视的课题。
2)广东海域单桩基础初始自沉的时候,粘土的设计强度折减在[1,4]之间较为合理,在计算溜桩风险的时候,粘土的设计强度折减在[3,7]之间比较合理。
3)初始自沉结束后,锤击沉桩引起的循环荷载,会导致桩周土的“摩擦疲劳”效应,进而出现溜桩时土体阻力损失更加严重的现象。
4)根据本项目的数据,单桩的初始自沉深度非常接近20 t海床CPT的极限测试深度。
5)在分析自沉深度和溜桩风险的时候,CPT是非常可靠的测试手段,因此无论是从设计还是施工角度考虑,都应加强CPT在勘察中的应用。
Statistical Analysis of Self-Weight Penetration and Pile Running for Large Diameter Monopiles in Offshore Wind Farm
doi: 10.16516/j.gedi.issn2095-8676.2023.01.008
- Received Date: 2020-10-28
- Rev Recd Date: 2022-04-28
- Available Online: 2022-07-11
- Publish Date: 2023-01-11
-
Key words:
- offshore wind farm /
- large diameter monopile /
- self-weight penetration /
- pile running /
- strength reduction
Abstract:
| Citation: | WANG Hongqing, SUN Wei, LIU Donghua, REN Hao, TANG Dongsheng, FANG Hui. Statistical Analysis of Self-Weight Penetration and Pile Running for Large Diameter Monopiles in Offshore Wind Farm[J]. SOUTHERN ENERGY CONSTRUCTION, 2023, 10(1): 64-71. doi: 10.16516/j.gedi.issn2095-8676.2023.01.008 |
















































































 DownLoad:
DownLoad: